高中数学运算素养的问题、原因分析与对策

陈远强

（福安市第八中学，福建 福安 355000）

高中数学是学生高中阶段学习的主要科目，而数学运算是高中课程标准所明确提出的六大核心素养之一。因此，就高中数学运算素养进行探究、分析，并提出相应的对策，具有重要价值。

目前，高中生数学运算存在不少问题，概括起来主要有：（1）运算能力较弱，简单运算经常出错，出现思路对、算不会，一听就懂、一算则错等问题；（2）套错公式，公式无法灵活运用，尤其有关联的公式，如平面向量平行与垂直坐标公式；（3）遇到运算量较大、过程复杂、技巧性强、灵活性高的题目，就束手无策，如圆锥曲线问题；（4）运算途径选择不合理，运算过程繁琐，准确率就更低了。另外，通过近几年福建省高考数学试卷的分析统计，发现高中生在不等式、函数、数列、圆锥曲线、向量、导数等运算方面都存在严重问题，运算成为解题障碍，导致失分。

笔者结合近几年教学研究实践经验，认为高中生运算素养不够理想的成因主要有：其一，学生对基本的概念、定义、定理理解不透彻，知识间的内在联系梳理能力弱，公式记忆模糊，无法正确运用，从而导致运算结果出错；其二，部分教师因为课时紧张等因素的限制，只关注思路分析，教学中给学生预留的运算时间不足，缺少针对数学运算能力强化训练；其三，关于运算途径选择问题，相当一部分学生缺少科学分析预估，存在思维定势的问题。这些问题叠加在一起，学生的运算素养弱化问题自然得不到及时解决。据此，笔者提出如下提升高中数学运算素养的对策。

一、夯实基础，找准运算的切入点与落脚点

高中阶段，数学教师有必要要求学生了解并掌握几种比较关键的运算对象，包括数、式、向量、函数、数列、复数、平面解析几何等。实践中注意到，对运算对象的理解，如果不从基本概念入手，想要取得优异成绩可能性很小。只有明确基本概念，才能在面对运算对象时找准切入点与落脚点。因此，教师在培养学生数学运算素养时，应该将基本概念教学安排在第一步，让学生以理解概念为基础，结合图形，用数学语言与数学符号表达出正确的想法。例如，如图1，在学习任意角三角函数的概念时，教师先对基本概念进行引导，再让学生在直角坐标系中，以点的坐标将锐角三角函数表示出来，在此基础上引入单位圆。这样有条不紊地组织教学，引导学生梳理知识间的内在联系，能给学生提供必要的思维发展支持，对三角函数的概念理解更透彻。同时，也能为推导得到同角三角函数的基本关系起到水到渠成的教学效果。

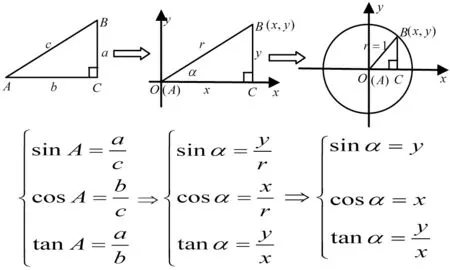
图1

sin2α+cos2α=x2+y2=1，tanα=加强基础知识教学，是数学运算素养产生与巩固的前提，虽然数学学科对于理解效果的关注度较高，但牢记基本概念、定义、定理和公式的必要性始终不容忽视。例如，学生将平方差公式与完全平方公式记错，错把（a=b）2=a2-b2，（a+b）2=a2+b2，必然会导致运算结果错误。再如，把向量平行与垂直坐标公式弄混淆=0），同样无法取得正确的答案。

A.4 B.1 C.-1 D.-4

部分学生错选了B 答案，究其原因是学生对平面向量平行坐标公式掌握不牢固，错用垂直公式运算。

解读《普通高中数学课程标准（2017 年版2020 年修订）》，新课标明确了运算的价值，从运算价值的角度展开分析，则能够进一步明确运算对象的内涵，即运算对象非常鲜明地展现出数学运算素养的载体依托功能，它通常来源于本学科乃至其他学科对实际情况的抽象。如果我们对运算对象进行深层次的探索，能够持续地拓展其应用领域，使数学应用广泛性特点得到充分彰显。

二、回归根本，强化数学运算能力训练

掌握基础知识后，教师应对数学教学只重视解题思维，却忽视运算过程的错误认知进行调整，要求与学生共同回归到数学运算本身。实践中，因为高中学生面临巨大的学业压力，时间紧、任务重，教师普遍突出思维训练，笔者认为转变这一认知，重视运算能力的培养训练非常必要。在平常的课堂教学过程中，教师应当突出运算作用，给予足够的运算机会及运算指导。学习三角恒等变换对两角差的余弦公式cos（α-β）推导时，教学中也应该要求学生对运用完全平方公式化简部分补充运算，利用课堂教学强化学生运算能力。因此课堂上教师应该适当增加运算环节占用的时间，引导学生补充遗漏的运算环节进行独立运算。此外，高中数学教师还应当从回归数学运算要求的角度出发，让学生在课后对平时训练、测试、考试期间的运算问题做出系统梳理，这将有效增强学生对运算环节及对应过程的重视程度。例如，部分学生在求y=（ex+e-x）的导数时，出现视复合函数e-x为ex的问题，导致失分。总之，教学中教师要指导学生正确运算，真正重视运算，在运算中发展数学素养。

三、克服定势，高效提升数学运算质量

部分学生在学习过程中，尤其在解题阶段，不可避免地采用自己固有的思维方式，新问题老办法，即使发现自身思维的不足，也不愿或不能改正，而一味追求多解题，却在解决好题与简便解题方面缺少前行的动力。针对这一情况，高中数学教师在教学中应能够给学生提供进一步引导，让其主动分析运算过程是否合理，以及出现错误、繁琐问题的原因，再找出更加恰当的运算方法，从思维与运算相结合的角度，让切入口变得更准，有机对比运算量大小、运算难度强弱、运算时间长短等。例如，如图2，M为抛物线y2=4x上的一点，F为抛物线的焦点，若以Fx为始边，以FM为终边的∠xFM=60°，求|FM| 的值？

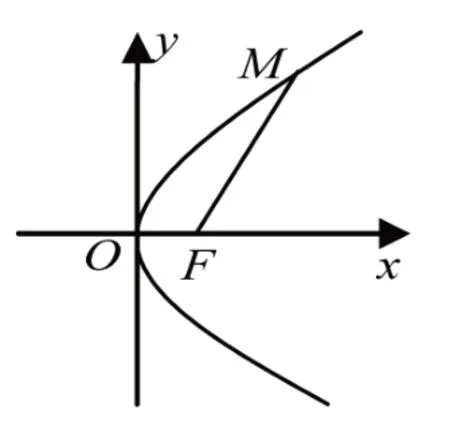
图2

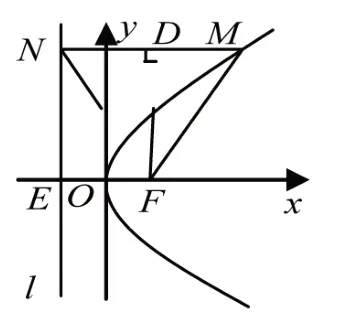
图3

对于该问题，学生的一般解题思路是先得到直线MF 的方程，再与抛物线方程联立，得到M点坐标，接着通过两点间距离公式，求出|FM| 的值。由于直线和圆锥曲线之间的位置关系问题，一般能够通过联立方程的策略加以解决，因此学生更容易想到这一方法，同时该方法入手较快，如思路一。

思路一：抛物线焦点F（1，0），直线FM的斜率kMF=tan 60°=所以直线FM：y=求出

若教师能够给予必要的引导，则学生还可以借助数形结合思想，从几何角度完成观察、探究，再进行其他形式的运算，如思路二。

思路二：如图3，过点M作MN⊥准线l，垂足为N，连接NF，由∠NMF=xFM=60°，MF=MN，所以△MNF为等边三角形，过点F作FD⊥MN，所以MN=2DN=2EF=4。

对比两种解题思路显然思路一运算量大，运算难度强，运算时间长，容易出错，而思路二运用抛物线的定义和数形结合思想运算量很小，运算效率高。

另外，教学实践过程中，为了达到克服运算思维定势的效果，教师还可以让学生彼此之间具有的协作意愿得到实现，让大家彼此交流，通过他人思维的长处，给自己的运算能力发展提供帮助。例如，在面对空间几何体表面积和体积的运算任务时，小组协作的做法非常值得尝试，教师要求学生在各自的学习小组中，针对正方体、长方体以及圆柱、圆锥等不同模型完成制作与思考，并分别进行面积与体积的求解运算，具有较好的实施效果。

四、着眼素养，针对运算多元评价

最后，高中数学教师有必要基于发展与进阶的需求，教学中为学生提供多元化色彩更明显、持续性效果更突出的评价，评价重点指向学生运算素养发展的薄弱环节。在评价体系建立过程中，注意到学生个体间差异的客观存在，对于擅长不同领域运算的学生给予不同评价标准，让学生能够准确定位自身数学学习优点和不足，并及时进行运算思维与运算方法的调整。在针对运算多元评价过程中，笔者采用SOLO 分类法，这一来自于澳大利亚教育心理学者比格斯的分层评价策略，对运算的深度学习及运算素养视域下的学生学习状态、学习过程，对内容的理解程度等，都有较全面的参考价值。受此分类法影响，笔者将评价分为五个层面：第一层面，要求学生机械套用公式，完成简单数式运算；第二层面，要求学生掌握基本概念、定理、公式；第三层面，要求学生借助公式变形，化简数式；第四层面，要求学生掌握算理、算法，明确不同知识体系间的内在联系，对复杂运算题进行求解；第五层面，深入思考数学运算体系，并对运算本质进行挖掘，使之能够更加灵活地迁移至运算体系中去，实现素养的有机发展。其中前三个层面为浅层学习，后两个层面为深度学习，五个层面的评价共同为学生数学运算素养的表现分析服务，教师可在面对不同教学内容时，突出每个评价层面的作用，给学生提供既全面又具针对性的评价及评价后因势利导。

综上所述，高中生数学水平与多种智力因素相关，教学实践中教师在充分理解教学内容、认知教学对象的前提下，应多方研究智力因素对于数学学习结果的影响，优化学习过程和方法，促进学生以更大的耐心、更强的能力去面对复杂的运算任务，并持之以恒。