工程教育专业认证背景下《高等数学》的教学目标与要求研究
——以惠州学院电子信息工程专业为例

2021-07-19 08:28李文波洪佩璇

惠州学院学报 2021年3期

李文波，洪佩璇

（惠州学院数学与统计学院，广东惠州 516007）

2016年，中国成为国际工程教育《华盛顿协议》的正式成员，标志着我国高等教育国际化迈出了重要的步伐，顺应了工程教育的改革潮流.工程教育专业认证工作已经有了十多年的推广与发展.对于电子信息工程专业来说，要想提高专业的认可度、质量以及影响力，必须通过工程教育专业认证.

工程教育专业认证标准对各类课程的学分比例进行了规定，针对《高等数学》［1］课程面临教学内容多、课时减少的情况，急需合理优化整合教学内容，在保证内容体系完整性的前提下，能够有效地为后续专业课程学习提供基础知识保障.目前《高等数学》教学内容多而碎，往往以文、理科划分教学内容和教学要求，不能高效地服务于各具体专业的学习要求，教学内容缺乏针对性.

为提高《高等数学》对电子信息工程专业后续课程学习的有效保障和学生的工程应用建模能力，本文运用知识点量化统计、加权赋值分析和权重分析模型等方法和技术，研究了电子信息工程专业所需数学知识，在保证数学知识系统化的前提下，为该专业设计了具有针对性的《高等数学》教学目标与内容.

1 《高等数学》课程内容需求分析

电子信息工程专业是以电子技术为基础的信息领域相关的宽口径专业，该专业方向为嵌入式系统和射频系统分析与设计，再经过专业课知识结构方向的划分后，可分为通信电子线路方向、导航系统及微波技术方向、信号与信息处理方向.通过研究不同方向下的每门专业课，结合《电路分析》《电磁场与电磁波》《数字信号处理》等渗透基础技术知识的专业课程，再结合专业发展前景，分析了对《高等数学》知识的需求，通过建立理论与实际相结合的数学模型，为其设计了具有针对性、有效性的《高等数学》课程内容.

为方便数据图和表格的制作，对下文出现的《高等数学》知识点，做以下约定：H表示函数、W表示微分、D表示定积分、P表示偏导数、F表示方向导数与梯度、C表示重积分、Ql表示曲线积分、Qm表示曲面积分、G表示高斯定理、Bl表示变量分离方程、Y表示一阶线性微分方程、E表示二阶线性微分方程、X表示向量及其运算、S表示数量积与向量积、J表示级数、Hm表示函数展开成幂级数、Fj表示傅里叶级数、Fb表示傅里叶变换、L表示拉普拉斯变换、Z表示Z变换.

1.1 需求广度分析

1.1.1 通信电子线路方向

《电路分析》课程属于通信电子线路方向的必修基础课程，以现代电工技术的基本理论知识为主线，学习电阻电路分析与动态电路分析两部分内容，为后续《模拟电子技术》《数字电路》等课程的学习奠定理论基础.以《电路分析》［2］为研究对象统计《高等数学》各知识点的频数（每门课程出现的某一知识点的次数）（图1）.

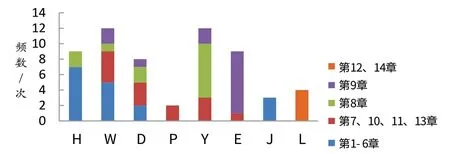
图1 《电路分析》课程对《高等数学》的需求广度分析

由图1可知，《电路分析》运用到《高等数学》的函数、简单微分、定积分、一阶线性微分方程和二阶线性微分方程五部分内容的频数分别为9、12、8、12、9，这就要求学生能重点掌握对函数极限、导数、微分、不定积分、定积分的计算以及一阶或二阶的常系数微分方程求解内容．

1.1.2 导航系统及微波技术方向

《电磁波与电磁学》课程属于导航系统及微波技术方向的必修基础课程，主要讲述静态电磁场、时变电磁场、平面电磁波、电磁波的辐射等内容，为后续《微波技术基础》等专业核心课程的学习奠定理论基础.以《电磁场与电磁波》［3］为研究对象统计《高等数学》各知识点频数（图2）.

图2 《电磁场与电磁波》课程对《高等数学》的需求广度分析

由图2可知，《电磁场与电磁波》运用到《高等数学》的定积分、曲线积分、曲面积分和向量及其运算这四部分内容的频数分别为16、16、28、29，要求学生能重点掌握同一个概念不同的微积分表达形式，以此来解决电磁问题、曲线积分和曲面积分的计算以及矢量代数与场论内容．

1.1.3 信号与信息处理方向

《数字信号处理》课程属于信号与信息处理方向的专业基础课，研究内容为信号处理的客观规律性，其理论和技术发展十分迅速、广泛应用于众多领域，为后续《通信理论》、《最优控制》等专业课程的学习奠定良好的理论基础.以《数字信号处理》［4］为研究对象统计《高等数学》各知识点频数（图3）.

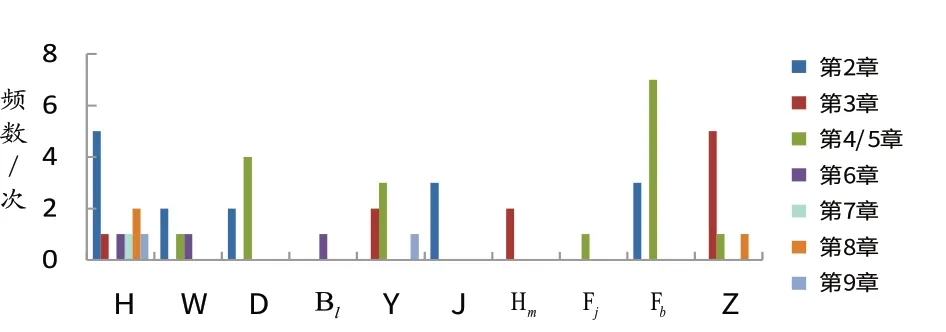
图3 《数字信号处理》课程对《高等数学》的需求广度分析

由图3可知，《数字信号处理》运用到《高等数学》的函数、定积分、一阶线性微分方程、傅里叶变换和Z变换这五部分内容的频数分别为11、6、6、9、7，这就要求学生能重点掌握卷积运算的应用、一阶线性微分方程的初等解法以及傅里叶变换与Z变换内容．

在统计《高等数学》各知识点的频数（p）时，将知识点的抽象度（c）、关联度（g）、推理度（t）分别赋值，得到表1.

表1 《高等数学》各知识点的广度赋值分析

由表1可知，知识点的广度受知识点频数和“抽象度、关联度、推理度”（统称为三维度）影响，从影响的范围、影响的持续时间长短及影响的变化频率出发，根据0-4对比评分法确定了知识点频数和“三维度”加权系数分别为0.4、0.6；将“三维度”的系数测评要素分类为具有可比性的数感、符号意识、几何直观、数据分析观念及模型思想，同样根据0-4对比评分法确定了“抽象度、关联度、推理度”偏重系数分别为0.2、0.5、0.3.由于三维度存在产生交集的情况，因而，所求平均数体现三维度的集中趋势，最终由下式

得到《高等数学》各知识点的广度指数（图4）.

图4 《高等数学》各知识点的广度指数

1.2 需求深度分析

为了适应工程教育专业认证发展需求，电子信息工程专业毕业生必须具有扎实的理论基础与专业基础知识，且能从事科学研究、设备或系统设计与应用等工作［7］.

基于工程教育专业认证核心理念，分析电子信息工程专业各项毕业要求［8］.记电路分析为1A、电磁场与电磁波为 2A、数字信号处理为 3A，专业课权重计算方法按Ai(i=1,2,3)课程是否为电子信息工程专业的学生学习后续课程起到前期理论依据为标准，若是，则将支撑指标点的所有课程权重分配到Ai(1,2,3)i=课程，再将3门课程的权重以1为总和进行重新分配，得到支撑指标点的3门课程各自的权重（表2）.

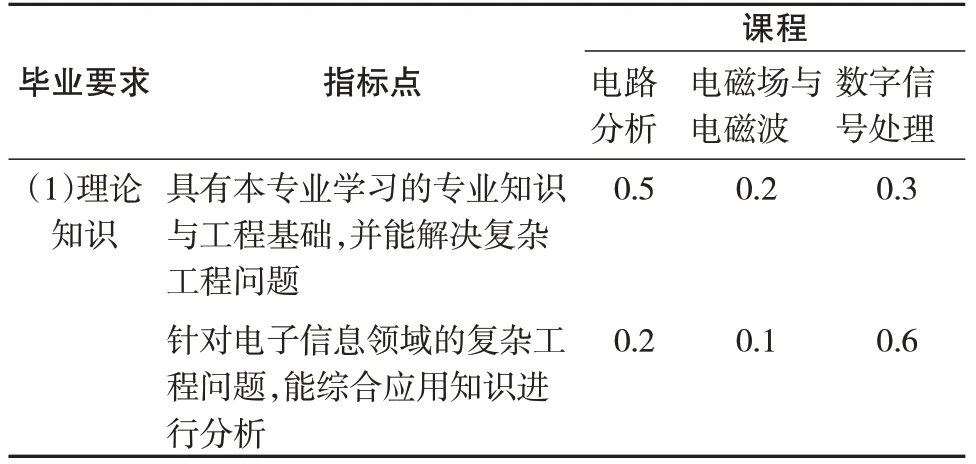
表2 支撑指标点的3门专业课权重分析

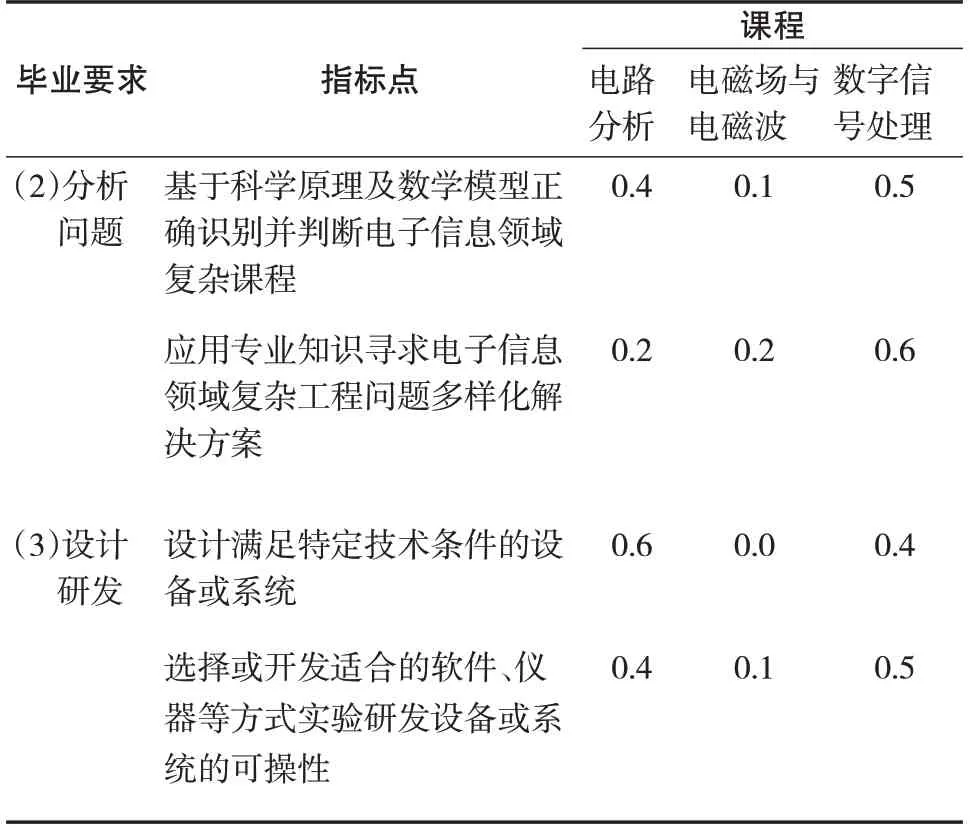
（续表2）

考虑到当前电子信息领域已广泛渗透于其他领域，其数字化、网络化、智能化逐渐明显，所以需要分析专业课程在电子信息领域前沿发展技术中的权重，以尽量满足课程权重分配的精确性.本文采用同样的权重计算方法，得到支撑前沿发展技术的3门专业课的权重（表3）.

表3 支撑前沿发展技术的3门专业课权重分析

为更直观、更简明体现课程的权重分配，对表2、表3的数据进行统计，并按下式计算专业课权重：

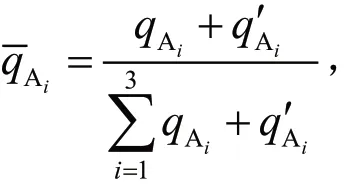
其中，为课程Ai的平均权重，qAi为课程Ai支撑指标点的权重，Aiq'为课程Ai支撑前沿发展技术的权重.《电路分析》《电磁场与电磁波》《数字信号处理》3门专业课的权重见图5.

图5 3门专业课的权重分配

支撑毕业指标点的专业课权重有所不同，而专业课对《高等数学》各板块的需求程度也不同.按出现的知识点所属板块先后顺序标记高等数学各板块，记一元函数微分学为B1、一元函数积分学为B2、……、积分变换为 B8，由下面公式

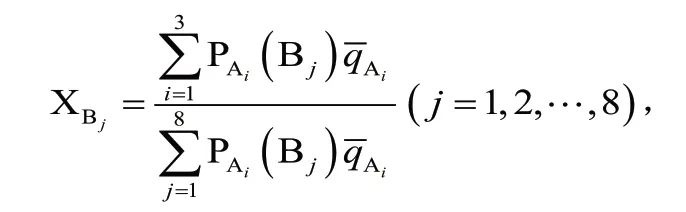
计算专业课对《高等数学》各板块的需求权重，其中XBj为Bj板块需求比重，PAi(Bj)为Bj板块在Ai课程出现的知识点频数总和（图6）.

图6 专业课对《高等数学》各板块的需求比重

按“知识点深度指数=该知识点在3门课程的频数和×该知识点所属板块比重”的方法计算《高等数学》各知识点的深度指数（图7）.

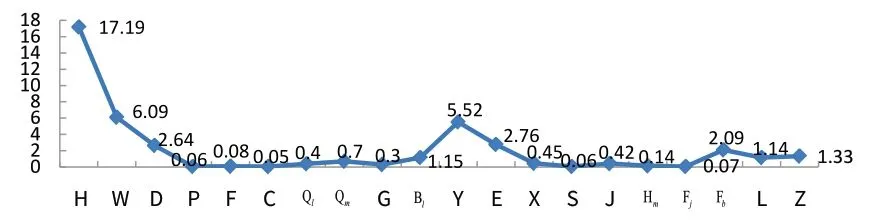
图7 《高等数学》各知识点的深度指数

2 《高等数学》课程教学目标与要求

通过对《高等数学》需求内容分析发现，对于电子信息工程专业学生来说，《高等数学》课程的教学目标是培养学生具有一定的空间想象能力、抽象思维能力、逻辑推理能力以及分析问题、解决问题的能力，因而《高等数学》课程更多服务于学生的工程能力，让学生学会应用数学知识解决实际工程问题的能力.

由图4和图7可知：一元函数微分学中的函数、微分的（广度指数，深度指数）分别为（1.2，17.19）、（1.24，6.09），因而一元函数微分学知识点的学习应占《高等数学》大篇幅.其中“极限”是一个重要的基本概念，无论是导数，还是定积分、广义积分、曲线的渐近线，乃至无穷级数等概念的学习都建立在极限的基础上.但极限的概念与理论是一元函数微分学的基础知识，并不是电子信息工程专业学生所需学习《高等数学》的重点知识.对于电子信息工程专业学生来说，对函数与微分的基本概念、基本理论、基本运算和基本应用等才是他们要熟练掌握及应用的内容.

因此，根据图4、图7呈现出的各知识点广度指数及深度指数，按照“必需、够用”设计原则，“必需”是在讲清基本概念的基础上，允许理论上的相对不完整性；“够用”则是在确保关键知识点的前提下，保证应用性知识的介绍，舍弃大部分理论推导与复杂计算［9］，从了解、理解、掌握与应用4个维度出发，规范电子信息工程专业的学生所需学习《高等数学》课程的各知识点的范围与程度（表4）.

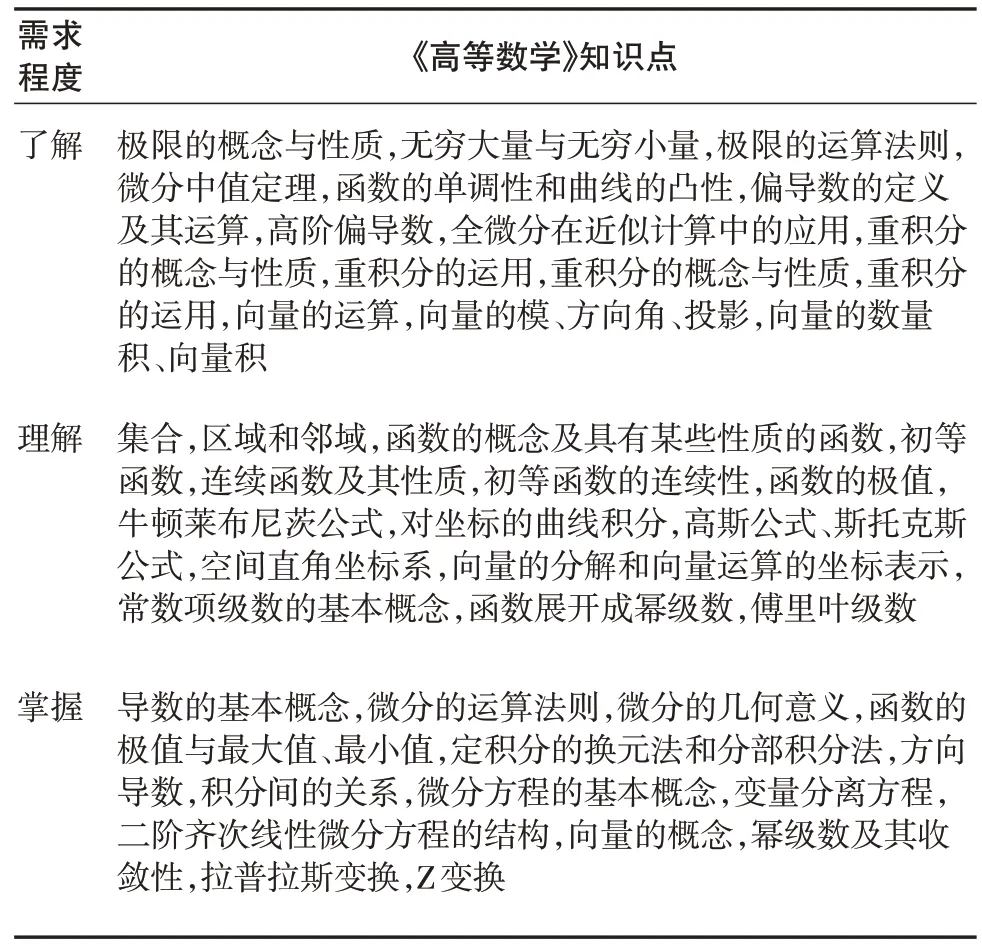
表4 电子信息工程专业所需《高等数学》各知识点程度

（续表4）

3 结论