D R值及其曲线的应用研究

李友仁 吕志华 秦少雄 宋 英

（陕西长岭纺织机电科技有限公司，陕西宝鸡，721013）

电容式条干仪是纺织厂必备的重要测试设备，对纺纱质量控制发挥着重要作用。条干不匀概括为两大类，即周期性不匀和随机不匀［1］。借助波谱分析解决纱线条干周期性不匀问题已很成熟，但对随机不匀至今仍缺乏深入分析。目前纺织厂常规测试纱线条干C Vm值和I P I值都是基于8 mm短片段线密度不匀曲线计算得出的统计值［2］，只反映短片段纱线条干随机不匀程度及瑕疵特征。全面分析纱线条干随机不匀应包括不同片段长度，它们之间并非有必然的相关性，即短片段状态良好并不能代表中、长片段状态也良好，因此须建立一种能够快速分析纱线不同片段长度随机不匀结构特征的新方法。

改善纱线条干均匀度的主要目的是为了获得良好的织物外观。多年来，衡量纱线条干随机不匀的指标主要是C Vm、C Vmb、C Vcb、I P I值，然后参照USTER2018公报进行评价。但实践表明，这些值即使达到USTER2018公报5%水平，也并不能保证获得良好的织物外观，由此推断产生这一问题原因可能是另外两个重要因素，一是纱线中属于小概率事件的过粗较长粗节和过细较长细节的占比；二是纱线线密度的分布状态。从C Vm值的数学定义来看，就决定了它只是从总体上评价纱线条干随机不匀，而与小概率事件的相关性并不密切；再是现在国内外纱线条干仪计算C Vm值时不涉及纱线线密度随机不匀的分布问题，一旦偏离正态分布，则所得C Vm值与织物外观相关性变差甚至完全不相关。

通过探索分析，上述问题可以借助条干仪测得的D R值及其他新指标得到一定的解决。引入D R值等指标，对分析纱线条干不匀结构更加有效［3］，尤其在全面评价纱线质量和预测织物外观方面有所增强。

1 D R（1 m，±5%）值的概念及应用

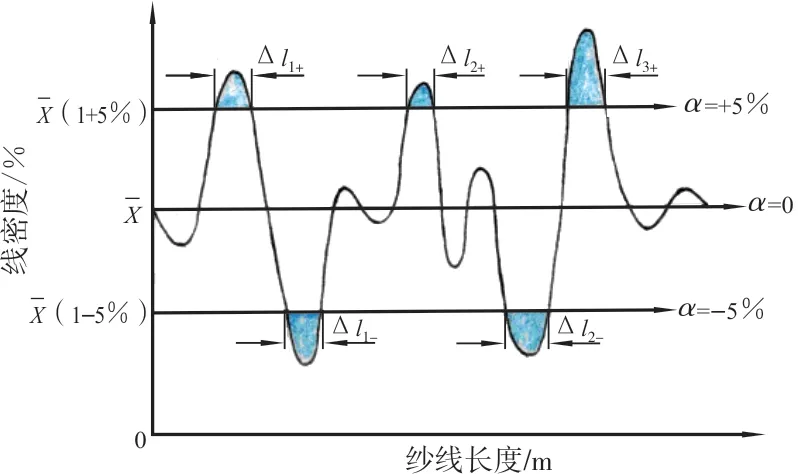
图1 条干仪测试纱线1 m片段长度不匀曲线

图1中阴影区分别表示粗细度超出平均线密度+5%及－5%的过粗较长粗节和过细较长细节。D R（1 m，±5%）分别表示纱线中过粗的较长粗节和过细的较长细节的累加长度占总试样长度L0的百分比。

本研究选择了1 m片段长度和±5%门限，这是基于：织物外观是靠目测进行评价，只当超过一定长度的过粗粗节和过细细节在织物上随机分布形成明显“条影”，才会刺激人眼产生直觉关注；常规百米称重法测试纱线线密度不匀，相对变化超过±3%会导致布面出现横档；D R（1 m，±5%）值相当于用1 m量级的相对变化超过±5%较长粗节和较长细节的程度表示线密度不匀，D R（1 m，±5%）值过大的纱线织成的织物必然会出现明显的“条影”。

C Vm值与有关，不同线密度纱线的C Vm值没有可比性。D R值则与无关，不同品种纱线的D R值可相互比较。所取门限α=±5%对不同品种纱线来说，虽然不同，但都取超出门限-X（1±5%）的粗节和细节，其相对粗细变化是一致的，当这些粗节和细节的占比相近，即D R值相近，且当线密度接近正态分布时则对织物外观的影响也是相近的。显然取D R值评价纱线质量就变得简单起来。不同品种纱线的线密度接近正态分布时，可依据D R（1 m，±5%）的平均值（1 m，±5%）对织物外观做出预判。当（1 m，±5%）≤9时，外观预判为“优秀”；当9<（1 m，±5%）<11时，外观预判为“良好”；当11<（1 m，±5%）<13时，外 观 预判为“ 一般”；当（1 m，±5%）≥13时，外观预判为“差”。

我们取USTER2018公报中两个针织品种管纱不同水平下的C Vm值和C V（1 m）值，并根据C V（1 m）值计算出不同水平下相应的D Rcal（1 m，±5%）值。当该纱线的线密度接近正态--分--布时，D Rcal（1 m，±5%）值可近似为实测D R（1 m，±5%）值，如表1所示。

从表1中看出，C V（1 m）随着C Vm增加也相应增加，可理解为这些统计值是建立在纱线线密度近似呈正态分布的前提下得出。从表1还可以看出，水平由5%到95%时，C Vm值的变化范围显然较D R值的变化范围要小得多，也即用D R值评价织物外观要较C Vm值更为敏感。线密度近似正态分布情况下，从统计结果看，C Vm值、D R值的水平优于50%水平时，织物外观随着水平提高愈趋优秀，而降到95%水平时，织物外观则显著变差。一旦线密度显著偏离正态分布，则C Vm、C V（1 m）（1 m，±5%）值之间相关性降低甚至完全不相关，所以仅凭C Vm值评价织物外观不够准确。

表1 两种纱线在USTER2018公报不同水平下的C V值与计算D R值

2 D R曲线及应用

目前长岭条干仪设计有5种切割长度（lc=1 cm、10 cm、20 cm、50 cm、1 m），并采用双线性坐标绘成D R曲线，这对于分析纱线随机不匀的结构特征具有创新意义。

2.1 正常D R曲线

正常纱线线密度接近正态分布，其不同片段长度的线密度不匀曲线围绕平均值总体上呈平稳地随机对称波动。反映在D R曲线上则呈现两个基本特点，一是相应门限α=0处各条曲线基本会聚于50%，即D R(l c，±0%)≈50%；二是相应纵轴（α=0）D R曲线左右对称且均匀分布，如图2所示。

图2 条干仪测试正常纱线的D R曲线

2.2 异常D R曲线

纱线中出现过多不同长度和粗度的偏粗粗节，此-时不同片段长度的线密度不匀曲线围绕平均值X总体上不再呈上下随机对称波动，而是朝粗方向显著多于朝细方向的波动，纱线线密度将不同程度地偏离正态分布。反映在D R曲线上于α=0处不再会聚于50%，而是错位突跳形成“左高右低”的“阶跃”且相对50%点上下基本对称。

为此，长岭条干仪给出一新的特征值——相对偏移系数 ΔD R(l c)，其中l c取1 cm、20 cm、1 m，用来定量评价“阶跃”的大小及方向。“阶跃”的大小以百分数表示；“阶跃”的方向“左高右低”时取正值，“右高左低”时取负值（正常纱线线密度接近正态分布，“阶跃”不明显，|ΔD R(l c)|<5%）。当ΔD R(1 cm)为一较大正值说明纱线中出现过多的短粗节；ΔD R(1 m)为一较大正值说明纱线中出现过多的较长粗节。当纱线中出现过多不同长度和细度的偏细细节，则在α=0处呈现显著“右高左低”的“阶跃”，ΔD R(l c)<0为一较大的负值。

下面通过几个实例说明，D R值及D R曲线异常，必然影响织物的外观。

2.3 几个生产实例

2.3.1 集聚纺JC 9.8 tex管纱

测试集聚纺JC 9.8 tex管纱，C Vm值、I P I值皆为USTER2018公报5%水平，但D R（1 m，±α%）曲线在α=0处出现显著“左高右低”的“阶跃”，且曲线向右拖长而显著不对称。ΔD R(1 cm)≈10%，ΔD R(1 m)≈16%，说 明1 m片段线密度显著偏离正态分布。D R（1 m，+5%）不是很快衰减到0而仍有相当大的值，说明纱线中出现异常长粗节且必影响织物外观。实测D R曲线如图3所示。

图3 “左高右低”的D R曲线

2.3.2 JC/T 60/40 7.4 tex管纱

测试JC/T 60/40 7.4 tex管纱，C Vm值、I P I值皆为USTER2018公报5%水平，但D R（1 m，±α%）曲线在α=0处出现显著“右高左低”的“阶跃”且曲线向左拖长而显著不对称，说明1 m片段线密度显著偏离正态分布。D R（1 m，-α%）不是很快衰减到0而仍有相当大的值，说明纱线中出现异常的长细节且必影响织物外观。实测D R曲线如图4所示。

图4 “右高左低”的D R曲线

2.3.3 JC 14.8 tex管纱

批次测试JC 14.8 tex管纱，4#、8#管纱的D R曲线如图5所示。两试样的D R（1 m，±α%）曲线在α=0处没出现明显“阶跃”，左右也基本对称，说明两试样的1 m片段线密度不匀曲线围绕平均值仍接近保持上下随机波动。又两试样的C V（1 m）值无显著差异（分别为3.28%和3.77%），但（1 m，±5%）值相差悬殊（分别为3.04%和15.08%）。再者两试样的理论计算值D Rcal（1 m，±5%）（分别为6.38%和9.25%）与实测平均值（1 m，±5%）（分别为3.04%和15.08%）差异显著，即两试样的1 m片段线密度明显偏离正态分布。

图5 有长片段线不匀的D R曲线

基于上述特点可对两试样1 m片段线密度--随--机不匀的结构特征做出解释，即4#试样的D R（1 m，±5%）值异常减小，说明纱线中随机出--现--一些异常均匀的纱段；而8#试样中的D R（1 m，±5%）值异常增大，说明纱线中随机出现一些异常不匀的纱段。此时1 m片段线密度不匀曲线不再是平稳地上下随机波动，而是随机出现一些波动幅度明显变小或是明显增大的纱段。

又两试样的C Vm值近乎相同以及I P I值皆处于USTER2018公报25%优良水平，短片段D R（1 cm，±α%）曲线也正常，但由于纱线中有的随机出现一些异常均匀的纱段，有的随机出现一些异常不匀的纱段导致D R（1 m，±5%）值离散很大（S值大于2%），而使织物外观恶化。

3 D R（1 m，）特征值的应用

4 纱线线密度分布的快速判断

4.1 判断方法

我们将C Vm值与D R值相结合，推出D R值相关系数和散点图，可快速判断纱线线密度是否接近正态分布，这一功能在长岭条干仪上已经实现。

当纱线线密度呈正态分布时，理论上不同片段长度线密度的D R值与C Vm值之间的关系由下式决定［4］。

式中：l c为切割长度或片段长度由“标准正态分布的分布函数值表”查出，y是积分中设定的自变量，将上限∞及下限带入后即可得出积分运算结果。

单管测试时，根据实测C V（1 m）值计算出相应的理 论D Rca（l1 m，±5%）值 。当实 测D R（1 m，+5%）与D R（1 m，-5%）--值--两者相近（即D R曲线左右对称），其平均--值--为D R（1 m，±5%），且当D Rca（l1 m，±5%）≈D R（1 m，±5%），即理论计算值与实测值相近，说明该管纱样的1 m片段线密度接近正态分布。

批次测试（一般取10管纱，测试速度400 m/min，测试时间1 min）时，每管纱的（1 m，±5%）≈D Rca（l1 m，±5%），且所测10管纱的C V（1 m）与相应的1 m，±5%）呈正相关，说明该批次纱线的1 m片段线密度总体上近似呈正态分布。可基于对D Rca（l1 m，±5%）、（1 m，±5%）值计算其线性单相关系数r值和绘成散点图进行实时判断。

当r值越大于0.9且散点图上诸点靠近45°线，说明该批次纱线的1 m片段线密度总体上接近正态分布。当r值越小于0.9和散点图上诸点分散偏离45°线，说明该批次纱线的1 m片段线密度总体上显著偏离正态分布。

4.2 实测验证

集聚纺JC 9.8 tex机织纱的散点图如图6所示。由图6可以看出，（1 m，±5%）≈D Rca（l1 m，±5%），即D R曲线皆正常；D R值的相关系数r=0.94（大于0.9）且散点图中诸点都靠近45°线。说明纱线1 m片段线密度总体接近正态分布；D R（1 m，+5%）、D R（1 m，-5%）的标准差分别为S+=0.83%及S-=0.77%（小于2%），即离散不明显，且总均值（1 m，±5%）=7.99%，比较小；可认为本批次纱线质量及织物外观皆优良。

图6 集聚纺JC 9.8 tex纱的散点图

JC 14.8 tex针织纱的散点图如图7所示。由图7可以看出，D R值的相关系数r=0.53且散点图中诸点分散偏离45°线，说明纱线1 m片段线密度总体以非正态分布。总均值=8.52%虽 不 大 ，但D R（1 m，+5%）、D R（1 m，-5%）的标准差分别为S+=3.54%、S-=3.12%，即D R值离散过大。虽然常规测试项目C Vm、C Vmb、I P I疵点值皆处于优良水平，但本批次纱线的最终织物外观较差。

图7 JC 14.8 tex针织纱的散点图

5 结论

综上所述，纺织厂仅凭常规测试C Vm值、I P I值、C Vmb、C Vcb值评价纱线条干不匀不能全面反映纱线的质量水平，尤其对布面质量方面。除了常规测试之外，可检测D R值和D R曲线，以评判布面质量，如下情况布面质量将处于良好状态。

（1）批次测试C V（1 m）与呈正相关，即相关系数r>0.9且散点图中诸点皆靠近45°线。

（2）每管纱的D R（1 m，+5%）≈D R（1 m，-5%）（相对偏差处于15%以内）且D Rca（l1 m，±5%），无显著差异。

（3）批次测试D R（1 m，+5%）值、D R（1 m，-5%）值离散不明显，各自的标准差S+及S-皆小于2%。

（4）批次测试D R（1 m，±5%）的总均值较小，纱线中未出现过粗的较长粗节和过细的较长细节

（5）D R曲线5组均匀分布，左右基本对称，无异常的向左或向右拖长以及密集、扭曲现象，在α=0处各条曲线汇聚于50%，无明显的“左高右低”或“右高左低”的“阶跃”，即相对偏移系数|ΔD R(l c)|小于5%。