植物染色纺纱测配色模型研究

王云鹏 姜 伟 张建明 金凯震 姜 展

（1.青岛大学，山东青岛，266071；2.德州恒丰纺织有限公司，山东德州，253500）

植物染料是从植物的根、皮、种子、果实、花等部位提取的色素制成的染料，银杏叶、杏仁壳、指甲花、芦木等色素提取物都可以应用于纺织品染色［1］。植物染无毒无害、色彩自然，且原料具有可再生性，可应用在棉、麻、羊毛、蚕丝、锦纶等纤维材料上，在国内高端市场具有广阔的发展前景。然而植物中色素含量低，植物染的成本高；植物染料的染色性能差、上染率低、色牢度低等缺陷也一直限制着植物染的发展［2］。

常用配色模型包括Stearns⁃Noechel模型、Friele模型、Kubelka⁃Munk模型、BP神经网络等。目前应用最为广泛的是Kubelka⁃Munk模型，但研究表明Kubelka⁃Munk模型是基于均匀散射的理论和情况下，并不适用于色纺纱；Stearns⁃Noechel模型与Friele模型相较具有更为优良的配色表现［3］。在实际生产过程中不单纯是三原色的简单配比，很多时候会出现需要用原有白色纤维进行混和的时候。Friele模型在实际研究的配色中会产生以下几个问题：一是在矩阵运算中加入白色反射率构成多组分配色极易与原有三原色反射率构成0向量；二是添加了新的反射率数据会使矩阵运算精确程度加大，误差更加明显；三是Friele模型是一种基于理论的模型，其运算结果可能会出现负数情况，不符合实际的工业生产［4］。本研究选择Stearns⁃Noechel配色模型为研究重点。

1 试验方案设计与配色模型分析

1.1 问题分析

基于植物染色纺纱的计算机测配色需要考虑众多实际生产带来的影响。一是配色模型是否符合工业生产情况和生产模式，需要适合的原料与配比方式。二是植物染上色不均匀导致的局部色差问题会使获取的反射率数据不稳定，影响测配色的准确性，需要改进测色样品。三是植物染料的色牢度不高，在工业生产中会产生掉色等情况，大幅增大了拟合配比与实际配比情况的差距，对此需要对配色模型进行一定程度的修正处理。

1.2 Stearns⁃Noechel模型分析

Stearns⁃Noechel模型的拟合公式见式（1）和式（2）。

式中：X1、X2、X3、…、X n对应不同组分占总质量的比例，r（i，n）表示不同组分不同波长下的反射率，M为配色公式中与材料相关的未知量，rm（i）为拟合的色纱反射率，f（X，M）为配色公式中的相关代数。

由公式（1）可以看出Stearns⁃Noechel配色模型实际上是对不同颜色纱线的反射率进行一定比例的拟合，基于人视觉的反射率系数运算后求得在视觉上与标样最接近的反射率时的配比。Stearns⁃Noechel模型在运算中的各组分拟合配比是通过不断循环求出拟合反射率与实际反射率色差最低时的配比，且配比的求得与标样的颜色种类无关，因此在原公式的基础上加入白色或其他颜色纤维时不会对后续的配色运算产生影响。通过对模型的分析与实际的配色拟合，发现该模型较适合多种不同颜色组合的配色。

红、黄、蓝、白四组分的Stearns⁃Noechel模型配色公式见式（3）。

经过针对不同组分的配色模型试验分析，Stearns⁃Noechel模型对于红、黄、蓝、白四者相互不同混和有着优异的适应性，分类配色有以下优点。一是针对不同情况，去除生产中不会添加的组分，更加符合实际生产；二是分类配色可以减少不同组分组合之间配色存在的相互影响，提高配色的准确性；三是分类配色同时令不同组分的相互影响因素独立出来，便于后续的改进。

1.3 试验样品制备

选用CM⁃2300d型分光测色仪，测色方便快捷；原料为茜草、姜黄、靛蓝植物染色莫代尔纤维与白色莫代尔纤维，由山东恒丰集团有限公司提供。将不同染色的莫代尔纤维以及不同质量比例的混和纤维经过“开松→混和→梳理→并条→粗纱→细纱”工序后获得对应的棉网以及细纱，将其中的细纱在一个3 cm×4 cm的黑色板上均匀紧密缠绕3 cm×3 cm面积大小以制成测色样品。均匀紧密地缠绕在一定程度上减小了测色时产生的色差，缓解了染色不匀导致的反射率数据偏差过大的问题，如图1所示。最终以不同原料和组合的棉网与细纱样品作为测色用试样。

图1 样品示意图

2 试验结果与改进

2.1 标样与样品种类的选择

以纯色原料制成的试样作为配色中的标样，不同原料混纺制成的试样作为样品。不同类型的标样与样品组合对计算机测配色的准确程度具有不同程度的影响。为寻求最佳的测配色标样与样品类型，采用纤维网与细纱两种不同的标样与样品相互组合，以此拟合配比得出最合适的样品类型。样品中红、黄、蓝、白成分赋予代号R、Y、B、W。不同样品测配色拟合配比见表1。

表1 不同样品反射率测配色拟合配比

在计算机配色过程中，由于拟合机制是计算所能达到的最小色差时的拟合配比，因此当拟合配比与实际配比越为相近时，拟合效果越好，最终生产纱线与样品的色差会越小。误差值取拟合配比与实际配比各纤维成分中最大误差，误差值的计算见式（4）。

式中：Δ为拟合配比与原配比的误差值，X n拟合配比为各组分的拟合配比值，X n原配比为各组分的原配比值。

由表1可以看出，棉网与细纱相互之间配色结果与实际配比的误差值过大，普遍在2到3之间，拟合结果都不理想；棉网标样与棉网样品以及细纱标样与细纱样品的配色与实际配比的误差值均在1.0左右，较为符合实际配比情况；其中细纱标样与样品的误差值多小于1.0，棉网标样与样品的误差值多大于1.0，可见细纱标样与样品的配色效果最为稳定。因此选用细纱标样的反射率与细纱样品进行配色可以提高测配色的准确性。

2.2 修正改进

由于染色与生产的不稳定，在试验过程中出现过部分配比与预期异常的情况，在分析原因的过程中发现不同标样的反射率中有以下现象：不同波长下，棉网反射率高于纱线的反射率数据，棉网的反射率数据与纱线的反射率数据在一定的比例范围内，一般在1.2～1.3。

由此可以假设在纺纱过程中的环境因素影响以及不同纱线之间的相互影响偏向于作用在纱线的整体，即在生产过程中产生的掉色与染色纤维之间的相互作用均匀体现在整个色纱上，针对这个推论可以在原有配色公式的基础上增加修正系数并初步设定修正系数范围在0.8～1.5之间，以达到拟合修正实际生产因素的效果。同时基于工业生产中不同的生产环境和生产条件，选择在不同配色模型中处理，也适应加入修正系数达到配色的准确与稳定。

式中：t1、t2、t3、t4分别为红、黄、蓝、白植物染莫代尔纤维的修正系数。在拟合试验过程中发现配色模型中的M变量在一定范围内对配色拟合的结果影响不大，基于此，将固定配比的混纺色纱反射率、固定配比的数值、各组分的反射率数据以及预先拟合出的相近M值代入，获得修正系数并进行式（6）的计算。

式中：i表示4种不同色纱（i=1，2，3，4），j表示第n个样品，tij为同一种类型的组合下不同配比时所计算得到的各组分的修正系数，如t12为某一组合下第2个样品反射率计算所得到的红色修正系数，t1为最终所得到的对应组合下的红色修正系数。首先使用未加入修正系数的原模型进行模拟配比，计算对应的M变量，将纱线实际配比与M变量代入式（5）中，经过计算机循环模拟，对比获得此配比下拟合色差最小时的修正系数t1j、t2j、t3j、t4j，代入式（6）得t1、t2、t3、t4作为该组合类型的配色修正系数。例如：计算四色组合（R∶Y∶B∶W）的修正系数时，求得3∶2∶3∶2、3∶3∶2∶2、2∶3∶3∶2样品下原模型时的3个M值，将M值与对应的配比代入式（5）求得t11、t21、t31、t41、t12、t22、t32、t42、t13、t23、t33、t43，将其代入式（6）得t1、t2、t3、t4，即R、Y、B、W配比组合的修正系数，此R、Y、B、W组合下的t1、t2、t3、t4分别为1.080、0.417、1.268、1.215。通过此方法计算所得不同组合下的修正系数见表2。

表2 不同组合下各组分修正系数

各组合的修正系数代入配色公式（5）中对各配色组合中其他配比的混纺纱进行修正配比拟合，得出表3修正后的模拟配比与误差值，可进行各组合修正前后拟合的配比以及模拟配比与实际配比的误差值对比。

表3 修正前后细纱组分反射率配色模拟误差对比

通过表3中修正前后模拟配比与实际生产配比的误差值可以看出，原先红、黄、蓝配色与原配比的误差值在1～2，经过修正后误差值均缩小到1以内，在各组合中经过修正后的拟合配比与实际配比的误差值相比于原拟合配比与实际配比的误差值在整体上减小，尤其对于误差值较大的组合更为明显，因此修正后的拟合配比更加接近实际的配色比例，在实际配色中与原色纱的色差会更小。在同一组合下不同误差值较为平稳，修正后部分拟合数据有较大的改进，说明在稳定生产条件下修正系数的添加对于同一配比组合具有明显的修正效果。

2.3 试纺验证

由配色模拟获得较小的配比误差值可初步实现精确稳定的配色模型，之后再根据未修正的模型与添加修正系数后的模型模拟的配比进行试纺，通过对修正前后试纺样品与原样的色差对比观察实际生产上修正系数添加的效果。表4为部分第一次试纺的细纱与原配比混纺纱的色差对比。由于植物染料的色牢度与染色的不稳定性，在实际纺纱中纱线与目标颜色的色差要比化学染高，难以达到稳定的配色效果。由表4可以看出，经过修正后所纺的色纱与目标的色差小于原模拟配比与目标的色差，对于模拟配比在实际生产上有较大改进，修正模拟后在第一次试纺中色差的减小说明修正系数的添加对于实际生产具有积极的效果，可以有效减少实际生产中植物染色牢度的不稳定对配色模拟准确性的影响，平衡有关产生色差的各种影响因素，对于生产环境等问题带来的严重配色差距有着明显的效果，以便减少后续修色的次数而更加有利于实现生产目标。

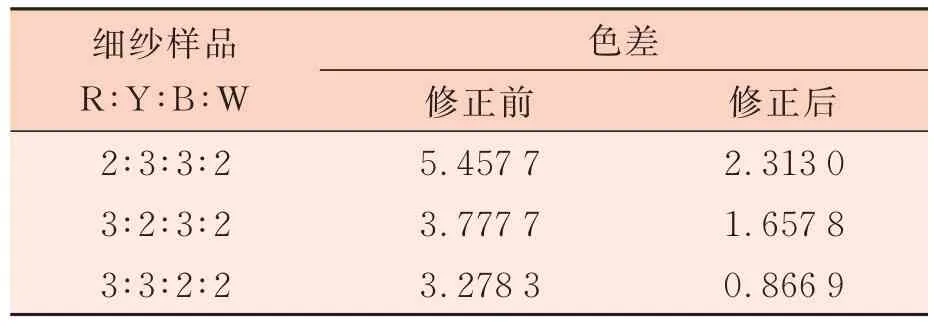
表4 修正前后第一次试纺色差对比

3 结论

在经过不同配色模型、样品、比例等试验与分析可得出以下结论。

（1）Stearns⁃Noechel模型在实际生产中具有优良的适应性、准确性和稳定性，可适应于色纱中多种不同组分组合的生产工艺；在棉网与细纱样品中，由细纱所制成的样品在配色方面更加准确和稳定。

（2）分类配色与修正系数可以在一定程度上减小不同色纺纤维间的相互影响产生的各组合间的配色准确性差距；修正系数的添加可以一定程度上减小色纺纱掉色等问题的影响，令数据的处理更加适应于实际生产情况。

（3）针对植物染色纺纱进行的配色模型处理是基于生产条件与原料稳定的情况下，减小实验室中第一次试纺色差可以加速模拟到成品之间的流程，一定程度上改善植物染掉色严重等带来的配色困难问题，对于植物染中原配比模型误差较大的情况具有明显的改善，不失为一种有效、便捷的修色方式。