一种基于动力学模型的弹性模量理论估算误差分析
蒋鹏程,王爱文
(北京信息科技大学 理学院,北京100192)
0 引言
弹性模量是工程材料重要的性能参数,是衡量物体抵抗弹性变形能力大小的物理量。弹性模量的准确测量对复杂环境下结构力学性能的预测和精密仪器的设计有着非常重要的意义。
弹性模量可以通过测量最大最小频率[1]和多阶固有频率[2]间接获得;另外,许多学者[3-4]通过改变结构表面的施加载荷,测量其中心弯曲挠度的变化之后通过计算获得。比如,Vikash等[5]用激光测量由温度改变引起的板中心弯曲挠度,估算与温度相关的板的弹性模量。Ayhan等[6]使用试验机测量单板层积材在载荷下的挠度,计算单板层积材的弹性模量。
上述实验结果依赖板中心的弯曲挠度。通常的弯曲挠度测量过程如下:在两侧简单支撑的板中心表面放置一个矩形条,改变施加在它上面的载荷量,测量板中心的弯曲挠度。弹性模量的计算是基于板条施加一致载荷的假设。然而,由于结构加工的差异,板条与结构表面之间的接触是不均匀的,载荷可能仅施加在几个接触位置。此外,放置中心的板条位置可能会发生偏斜,这些因素对弹性模量计算准确性的影响程度直接关系到工程中的应用与设计。
1 模型建立
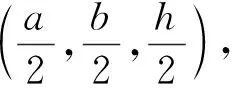
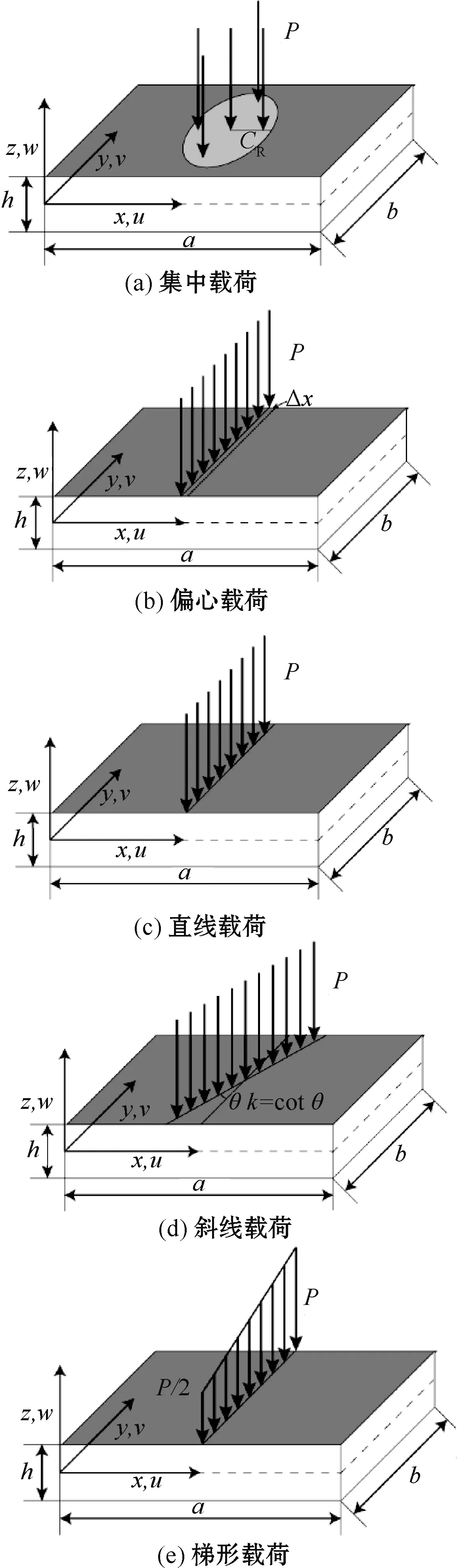
图1 载荷类型
本文以长为a、宽为b、厚为h的功能梯度板为研究对象,如图2、图3所示。其等效材料参数P(z)以体积分数幂率的方式在厚度方向梯度分布:
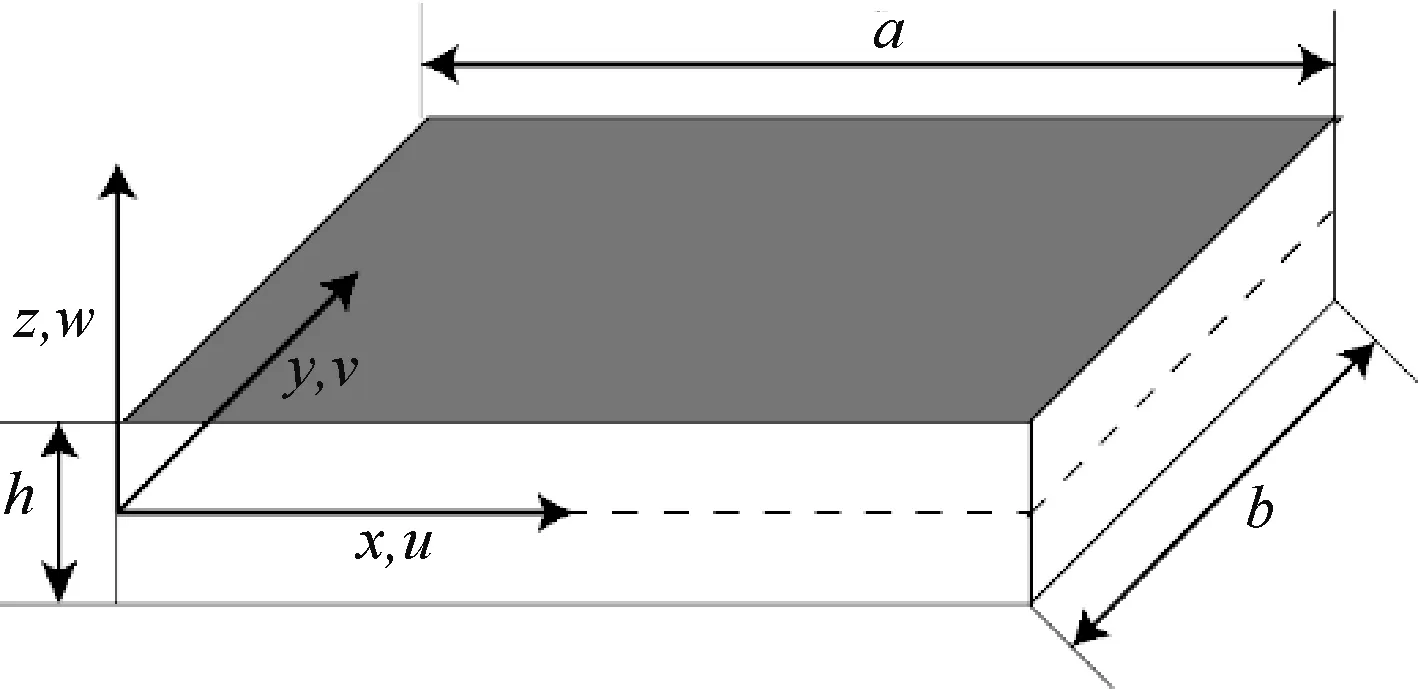
图2 功能梯度板示意图

图3 功能梯度材料截面
P(z)=P1+(P2-P1)V2(z)
(1)
(2)
式中:θ为体积分数指数;P1和P2分别为Al和ZrO2-1的材料参数,比如弹性模量、密度等。为了计算方便,沿厚度方向将板分为N层,每层的材料参数均根据式(1)、(2)计算。
令(u1,u2,u3)为板任意一点处在x、y、z方向上的位移,根据经典板理论位移场为
(3)
式中u(x,y)、v(x,y)、w(x,y)为板的中心层在x、y、z方向上的位移。
小应变假设下板的经典应变—位移关系为
(4)
式中“,”表示对下标求导。
假设ε和q有如下的向量形式:
εT=(εxx,εyy,εzz,γxy,γxz,γyz)
(5)
qT=(u,x,u,y,v,x,v,y,w,xx,w,xy,w,yy)
(6)
则应变ε的矩阵形式为
ε=ZHq
(7)
其中:
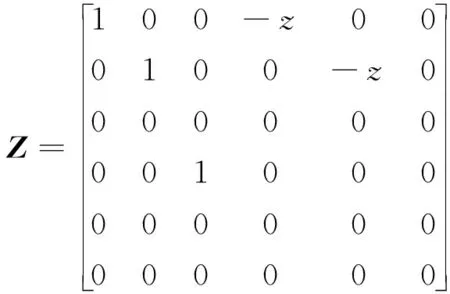
(8)

(9)
第k层的应力σ(k)与应变ε之间的本构关系为
σ(k)=Q(k)ε
(10)
其中:
(11)
内部虚功为
∬AδqTHTDHqdxdy
(12)
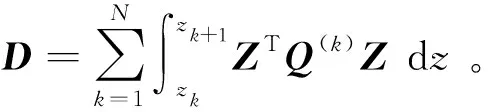
外部虚功为
δPext=∬AδqTpdxdy
(13)
式中p为作用于板上表面的外力。
运用虚功原理可得
∬AδqT(HTDHq-p) dxdy=0
(14)
2 数值模拟
以功能梯度材料板为例,进行数值模拟,各种材料参数、载荷参数如下:
a=b=1 m;h=0.2 m;N=10;
Rc=0.1 m;Δx=0.05 m;k=10。
A1和ZrO2-1的弹性模量E1、E2和泊松比v1、v2如表1所示。
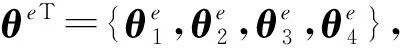
θeT={ui,x,ui,y,vi,x,vi,y,wi,x,wi,y,wi,xx,wi,xy,
wi,yy}e
(15)
代入(14),可得单元上的离散矩阵为
δθeT∬AGT(HTDHGθe-p) dxdy=0
(16)
合成得到整体刚度矩阵和载荷向量,便可以求得板的挠度。
边界条件为简支边界:
v=w=w,y=0y=0,a
u=w=w,x=0x=0,a
2.1 结果验证对比
为了验证本文理论的正确性,在不同的体积分数θ下,采用有限元方法计算的结果和文献[7]中Al和 ZrO2-1功能梯度板的结果一致,如表2所示。表明了基于有限元方法的模型和数值计算过程的正确性和有效性。

表2 在一致载荷下无量纲中心挠度的对比
2.2 载荷类型对弹性模量估计的影响
根据文献[8],弹性模量可以用式(17)表示:
(17)
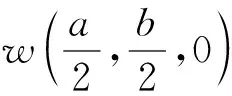
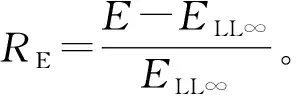
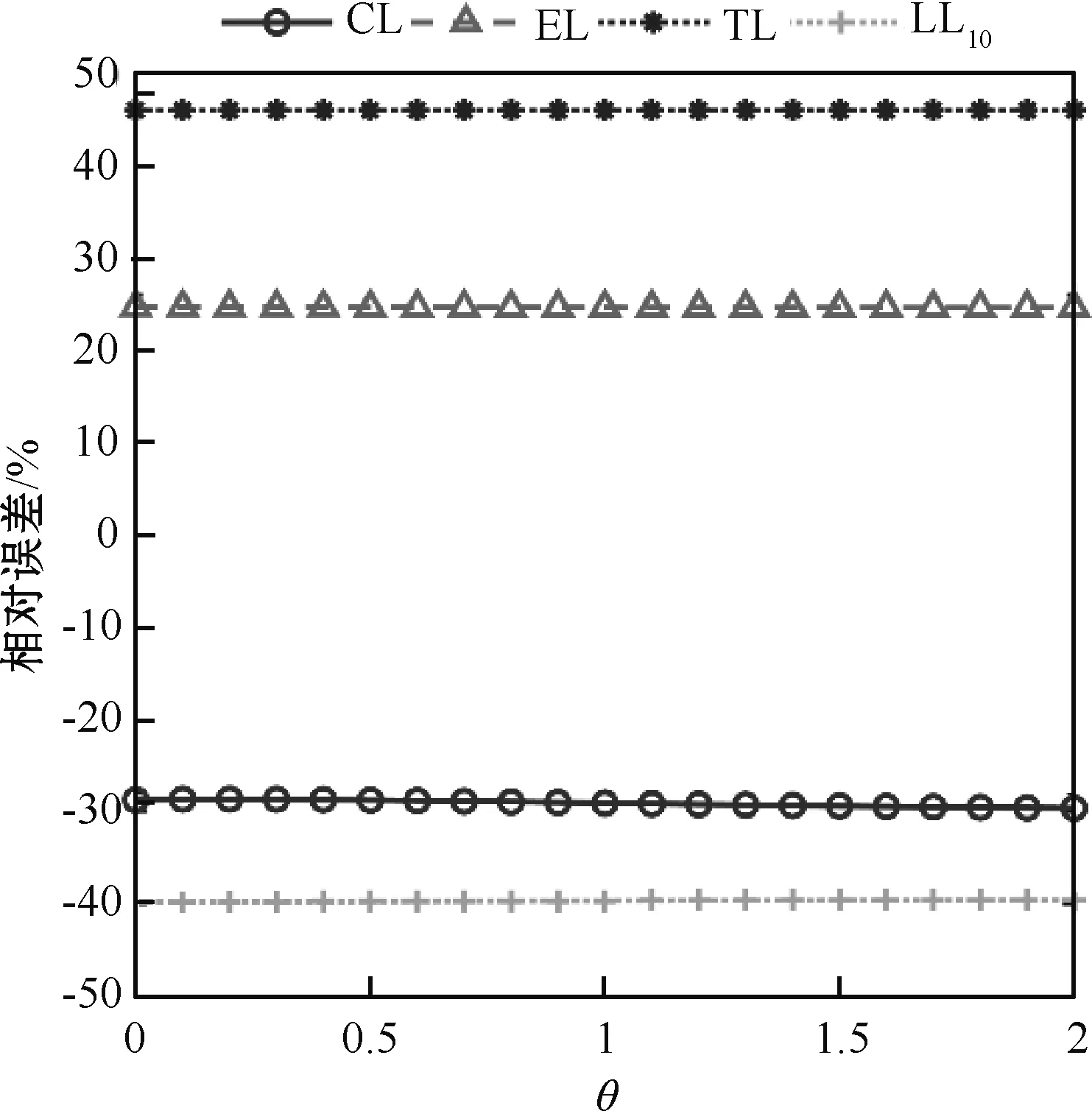
图4 体积指数、载荷类型对弹性模量估算的影响
固定体积分数指数为θ=0.5,图5给出了厚长比对误差的影响。弹性模量的估算误差随着板的厚长比提升而升高,因为经典板理论适用于薄板,因此越厚的板,误差也会越大,但载荷类型对误差的影响更大。

图5 厚长比、不同载荷对弹性模量估算的影响
表3给出了纯铝板基于不同载荷下弹性模量的估算的相对误差,并与功能梯度材料的计算结果进行对比,结果表明材料类型对误差的影响不大。

表3 不同载荷下纯铝与功能梯度材料的弹性模量相对误差 %
3 结束语
本文通过建立数学模型以及有限元计算,对施加在板上表面的线载荷发生不同偏差时对弹性模量的计算进行理论误差分析。数值结果表明,在材料相同的情况下,载荷类型对弹性模量的估算影响最大,尤其是梯形载荷和中心斜率为10的斜线载荷。同一载荷类型下,相对误差随着长厚比的增加而增加,材料对相对误差的影响不大。本文的结果为弹性模量测量过程给予了有益的借鉴。

