面向封装电源噪声抑制的人工电磁结构设计

李坤坤，缪 旻

(北京信息科技大学 信息微系统研究所，北京 100192)

0 引言

人工电磁结构(AES)是指将人工设计的具有特定几何形状的金属单元规则阵列排布，并植于介质所构成的复合功能结构，可实现自然介质所达不到的电磁特性。AES的研究经历了数十载的探索和验证，最早由前苏联物理学家V.G.Veselago于上个世纪60年代提出[1]，随后经过J.B.Pendry[2]和D.R.Smith[3]的验证和发展，最终由F.Capaso 在 2011 年提出了超表面的广义定律。该定律拓展了二维AES的应用范围，特别是在天线设计领域以及平面电路滤波器设计领域得到了进一步的研究和应用[4-5]。

电磁带隙结构(electromagnetic bandgap，EBG)属于二维平面周期AES。传统的EBG结构由于其本身面积较大，在系统封装等微型化、平面化(2维或者2.5维)电路中应用较为困难。为了实现EBG结构面积小型化的技术需求，众多专家学者做了广泛研究[6-8]。同时，增加电磁抑制频段的带宽，在微型电源网络结构或天线以及滤波器的设计中应用较广[9]。因此，缩小EBG结构面积，研发双抑制频段和多抑制频段EBG结构有着大量的市场需求和较好的应用前景。

目前大多EBG结构仅针对其中的某一问题进行研究。本文综合考虑EBG结构面积、抑制频带数量和应用范围情况，提出了一种新型EBG结构。该结构较传统型EBG结构(conventional mushroom-type EBGs，CMT-EBGs)在面积上缩小了65.4%，同时相比于CMT-EBGs仅仅拥有单抑制频段，新提出的结构增加了抑制频段的数量，这极大地提升了该结构在传输高速信号的系统封装和电路板上的应用范围。

1 人工电磁结构

AES能够实现独特的电磁特性，如抑制表面波或引导表面波的传播。AES的ε-μ参数象限空间划分如图1所示。自然界中的绝大部分材料处于第一象限(ε>0,μ>0)，支持正向传播的电磁波。由于该象限的材料对电磁波的传输满足右手定则，因此称之为右手材料(right-handed materials，RHM)。有少部分材料在某些状态下会在第二象限(ε<0,μ>0)，如等离子体以及位于特定频段的部分金属。电磁波只能在折射率为实数的材料中传播。当ε<0、μ>0时，电磁波的折射率为虚数，也即在这种材料中传播的电磁波只能是消逝波(evanescent waves)。处于第三象限(ε<0,μ<0)中的材料，电磁波传输时的波矢和能流方向是反平行的，满足左手定则，因此称之为左手材料(left-handed materials，LHM)[10-12]。麦克斯韦方程表明允许电磁波在满足第四象限(ε>0,μ<0)的材料中传播，但此时材料的折射率却必须取负值。

根据对AES电磁反射性不同的需求，可将其设计为高度各向异性的，且实现各种材料特性以及电磁学变换的灵活性，从而控制电磁波的传输，以增强其应用范围。

随着5G通信技术的快速发展和商用，可将EBG应用于制作定向天线、多频带滤波器等结构。同时，EBG结构也有望广泛应用在系统封装电源分配网络同步开关噪声的抑制中，用以提高传输性能，增加阻带带宽，增强其电源系统的稳定性。

2 电磁带隙结构的设计与仿真

2.1 新型电磁带隙结构的设计

蘑菇型(mushroom-like EBGs)电磁带隙结构是EBG经典结构，因此又被称为传统型电磁带隙结构(CMT-EBGs)，如图2 (a)所示。由于蘑菇型EBG结构制造工艺简单，因此大量地运用在电路板等二维电路与互连网络中，近些年来受到了国内外大量科研人员的关注。

EBG结构可以看作是一个特殊形状的LC电路，某些频率段的电磁波通过EBG结构时，会在EBG结构内部腔体中形成一个谐振回路，从而抑制该频段电磁波的传输。正如改变LC电路自身固有的谐振频率一样，通过改变EBG结构等效电感和电容的数值可以达到控制其等效LC电路谐振频率的目的。EBG结构的电容值由金属板之间的间隙距离来确定，而电感则由上平板和地平面之间的距离来确定。式(1)～(4)给出了CMT-EBGs的谐振频率ω0、电感L、电容C和带宽B的计算方法[13-14]。

(1)

L=μ0h

(2)

(3)

(4)

式中：w为CMT-EBGs单元的上平板边长；g为相邻两个EBG结构上平板之间的距离；h为通孔的高度；ε0和μ0分别为真空介电常数和磁导率；εr为介质层的相对介电常数。

CMT-EBGs的LC等效电路模型如图2 (b)所示。

图2 单元EBG结构模型及其等效电路图

将单元CMT-EBGs排列组合为3×3模型结构，其俯视图如图3所示。利用HFSS全波仿真软件对该模型结构进行扫频分析，得出其插入损耗S12参数如图4所示，图中S12参数表明电磁波在CMT-EBGs中传输时，其频率在1.75～3.15 GHz之间出现了电磁抑制频段，且衰减值均超过-10 dB。

图3 3×3CMT-EBGs俯视图

图4 CMT-EBGs插入损耗参数S12

由图4可知，CMT-EBGs仅仅存在一个电磁抑制频段。另外，CMT-EBGs本身的面积较大，很难满足系统封装或电路板等平面化电路系统的要求。针对上述问题，本文提出一种新型EBG结构。

根据式(1)～(4)可知，增加EBG结构的等效电容和电感数量会增加其电磁抑制频段的数量。其中，上平板刻蚀沟壑的数量增多可以增加其等效电容的数量，同时，通过刻蚀沟壑所产生的弯曲条状金属改变了上平板的等效物理长度，随着金属条状长度的增加进而增大了等效的电感值。因此通过控制变量法，在不改变其他参数的情况下逐步增多上平板的刻蚀沟壑，从而改变新型EBG结构的等效电容电感值，如图5所示。

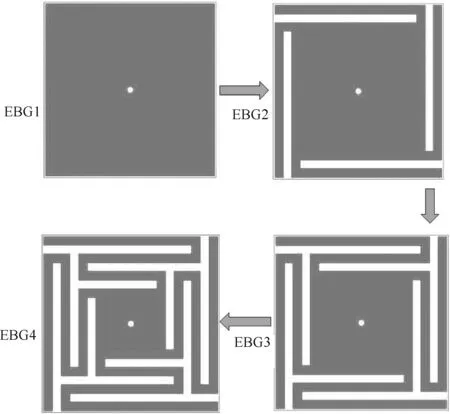
图5 新型EBG结构设计

由图5可知，EBG1结构与CMT-EBGs在几何上具有相似性，但是削减了上平板的宽度从而减小了其面积。EBG2结构在原有的EBG1结构基础上各方向增加了一条刻蚀沟壑，EBG3结构在EBG2结构的基础上向内靠近中心处再次增加了新的4条刻蚀沟壑，EBG4结构在EBG3的基础上继续增加刻蚀沟壑的数量。EBG4即为新型EBG结构，新型EBG结构的三维结构图、俯视图和截面图如图6所示。

图6 新型EBG结构示意图、俯视图和截面图

上平板条状之间的间隙可以看作是一个等效电容，而条状金属本身有电感属性，通过改变条状金属的长度从而改变等效电感值，新型EBG结构模型等效LC电路图如图7所示，其结构模型与CMT-EBGs的设计参数对比如表1所示。

图7 新型EBG结构等效电路模型

由图5可以看出，新型EBG结构和CMT-EBGs的差别在于调整了上平板的形状，通过在上平板中增加刻蚀沟壑空隙从而增加了等效的电容和电感数量。由表1上平板面积参数可得出新型EBG结构相对于CMT-EBGs在面积上缩减了65.4%。

表1 CMT-EBGs和新型EBG结构模型参数表

2.2 新型EBG结构全波仿真分析

为了验证新设计的有效性，将EBG1～EBG4结构按照3×3排列组合进行全波仿真。在0～10 GHz范围内利用HFSS软件对EBG1～EBG4结构进行扫频分析，其插入损耗参数S12如图8所示。

由图8可知，EBG1结构的插入损耗参数在3.2 GHz附近出现了仅有的1条电磁抑制频段；EBG2结构的插入损耗参数在EBG1结构的基础上在4.7 GHz处出现了第2条电磁抑制频段，但是其抑制程度较小；同样地，EBG3结构的插入损耗参数相比于EBG2结构在第2条电磁抑制频段的抑制程度上有明显的提升；EBG4结构其插入损耗参数具有3条较为良好抑制程度的电磁抑制频段，分别在2.1 GHz、3.5 GHz和7.0 GHz附近。

图8 EBG1～ EBG4结构插入损耗参数S12

将新型EBG(EBG4)结构与CMT-EBGs的插入损耗参数进行对比，如图9所示。由图9可以看出，CMT-EBGs在0～10 GHz扫频区间仅存在1个电磁抑制频段，而新型EBG结构则出现了3个电磁抑制频段，且其抑制程度均大于-10 dB，这极大地提高了电磁带隙结构的应用范围。

图9 新型EBG结构与CMT-EBGs插入损耗对比

在上述全波仿真基础上，利用HFSS后处理功能对3×3排列的CMT-EBGs和新型EBG结构的表面电流分布进行了提取，结果如图10所示。

图10(a)与(b)显示出在0.1 GHz通带处的表面电流分布均匀，表明该频率处的电磁波信号能够均匀且平稳地通过；由图10(c)可见，在2.1 GHz频率阻带处，新型EBG结构由于存在电磁抑制效应，其表面电流只有极小部分在中心衔接处通过，即对该频率的信号或者噪声有较强的抑制功能；同样地，新型EBG结构在3.5 GHz处的电磁抑制程度超过了-20 dB，由图10(d)可知，其表面电流仅仅在端口1的附近有极少的电流分布；由图10(e)可知，新型EBG结构在7 GHz处表面电流仅有一小部分在单元新型EBG结构边缘通过。

图10 EBG结构在不同频率处的表面电流分布

通过上述对比，印证了新型EBG结构的表面电流与端口S参数分析结果的对应关系，即电磁抑制频率(阻带)处仅有极少部分的表面电流通过，而其他频率(通带)处有相对较多且分布均匀的表面电流通过。进一步说明了新型EBG结构的电磁抑制效应的来源和有效性。

将该新型EBG结构应用于系统封装的电源网络时，电源网络所产生的处于新型EBG阻带频段的噪声通过该结构时，会在很大程度上受到抑制，因此新型EBG结构有望提升系统封装电源网络的稳定性。

3 结束语

CMT-EBGs本身面积较大且仅有1个电磁抑制频段，限制了其应用范围。综合考虑EBG结构的面积、抑制频带数量和应用范围情况下，本文提出了一种新型EBG结构。相比于CMT-EBGs，新型EBG结构在面积上缩减65.4%，并且电磁抑制频段的数量大幅增加，这极大地提升了该结构在传输高速信号的系统封装和电路板电源网络的噪声抑制方面的适用性。