双曲面压电复合材料温度稳定性研究

赵亚楠，王丽坤，廖擎玮

(北京信息科技大学 北京市传感器重点实验室，北京 100192)

0 引言

目前声呐系统在水下探测、通讯、导航、测绘等方面发挥着重要的作用。换能器作为声呐系统信号收发的核心部件，直接影响声呐系统的性能[1-3]。声呐应用领域的拓展，对换能器的性能提出了新的要求。目前换能器的发展方向主要是宽频带、大波束开角、高分辨率等。工作频带越宽，声信道就越宽，可使声呐系统探测距离更远；大的波束开角可使声呐的探测范围及观测视野更加广阔；高的分辨率可提高目标成像的质量和系统对小目标的识别能力。大波束开角高频换能器主要通过设计曲面压电元件来增大波束开角，比如，圆柱形水声换能器可以实现水平方向的全向覆盖；而双曲面水声换能器则可以实现换能器水平和垂直波束开角双向的拓展[4-5]。

双曲面压电复合材料作为双曲面水声换能器敏感元件使用的核心功能材料，其性能决定了水声换能器的性能。然而，由于双曲面压电复合材料是由高分子聚合物(如环氧树脂、橡胶)和压电陶瓷复合而成的，其聚合物的热膨胀系数远大于压电陶瓷，当压电复合材料所处环境温度出现变化时，聚合物就会发生形变，从而引起复合材料产生形变，继而导致换能器出现振动频率漂移、波束开角波动等情况，影响声呐系统的稳定性。当环境温度较高时，聚合物将产生较大形变，甚至可能会使压电陶瓷与聚合物的界面剥离，直接导致复合材料失效，继而影响换能器的使用。而对于南极北极科考应用，要求换能器在-40 ℃低温下稳定工作，这对压电复合材料低温稳定性提出了更高的要求。对于平面压电复合材料的温度形变已有一些研究，如白智奇等[6]应用光纤光栅法测试了平面压电复合材料长度、宽度和厚度方向的形变，并对介电常数和频率常数等数据进行了修正。然而，目前针对双曲面压电复合材料温度稳定性的研究较少，尤其是针对环境因素引起材料形变的检测及控制方法几乎未见，亟须就此开展研究。

目前材料形变的测量方法有很多种，主要包括应变片测量法、数字散斑干涉法、光弹性法和三坐标测量法等[7-11]。但这些方法存在接线方式单一、视场小、定性分析单一等缺点。相比较来说，光纤光栅(fiber bragg grating,FBG)测量法具有较高精度，可实现测量数据的高速率、大容量传输[12-14]，不失为一种有效测量压电复合材料形变的方法。因此，本文以光纤光栅测量法为基础，在-40～100 ℃的温度范围内对双曲面压电复合材料的形变和机电性能进行系统测试与研究，测量不同方向的形变，并测试不同温度下压电复合材料的机电特性。

1 实验测试系统及原理

1.1 光纤光栅测试压电复合材料形变原理

光纤光栅的反射波长对温度、应变等外界环境的变化比较敏感，其传感原理如图1所示。当光通过光纤光栅时，光栅会对入射的宽带光进行选择性反射，反射一个中心波长与芯层折射率调制相位相匹配的窄带光，反射波长由光纤芯的有效折射率neff和光栅的周期Λ决定[15]。

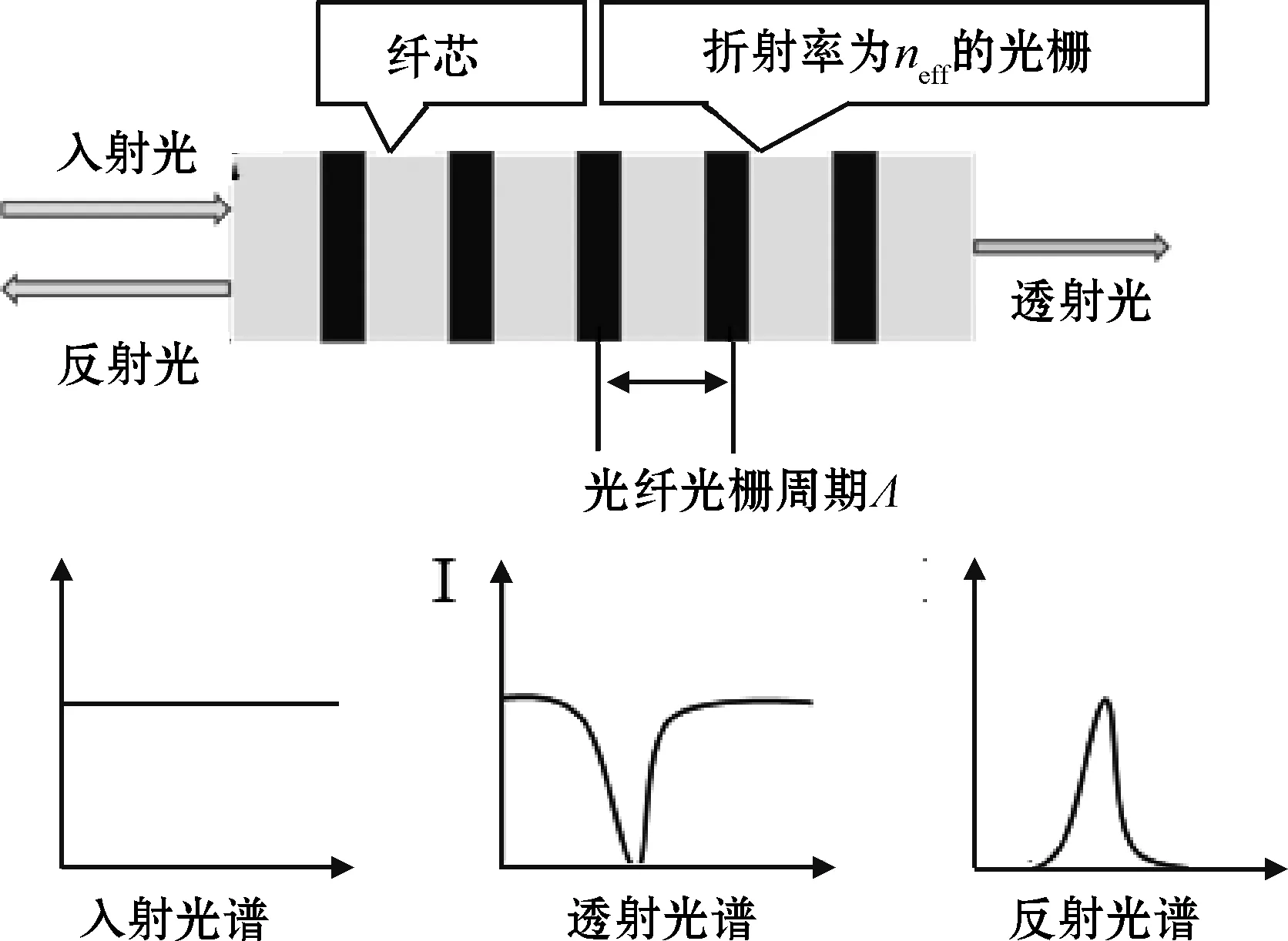
图1 光纤光栅传感原理

光纤光栅的反射波长可以表示为

λ=2neffΛ

(1)

如果拉伸或压缩光纤，即光栅发生应变，则neff和Λ就会发生变化，继而使反射波长发生变化。光纤光栅反射光的波长变化量与光纤光栅应变的关系为

(2)

式中：Δλ为光纤光栅反射光波长的变化量；ε为光栅轴向应变；P为光纤的泊松比。对于典型石英光纤，P=0.22，则光纤光栅波长变化量与应变的关系为

(3)

因此

(4)

在实验中，本文采用光纤光栅直接贴附压电复合材料表面的方法测量材料形变[16]。当压电复合材料发生应变时，将带动光纤光栅产生应变，通过计算光纤光栅的反射波长，便可以得到所对应处的应变ε。由于环境因素(如温度、湿度、气压等)作用于光纤光栅，同样可以引起光纤光栅反射波长的变化，因此通过光纤波长的变化检测得到的应变ε，包含有复合材料的应变εT和环境因素引起的光纤应变εE。为消除环境因素引起的光纤应变，测试时，本文设计1个等栅距的校准光栅悬置于测试环境中进行补偿。

ε=εT+εE

(5)

式中：εT为温度为T时试样的应变；εE为环境因素引起的光纤光栅应变，根据式(4)得到

(6)

则温度为T时测试点的试样应变为

εT=ε-εE

(7)

将某一方向所测不同点的光纤光栅应变值εT取平均值后可得到试样在此方向的平均应变值εA。将εA乘以对应方向的总长度L即可得到总形变E。即：

E=εA×L

(8)

1.2 光纤光栅粘贴方式及测试系统

实验中，为了减少测量过程带来的误差，采用1根光纤分布刻写多个光栅的方法，将光纤光栅沿试样三维方向连续分布粘贴，以测试样品3个方向的应变。测试时将光纤沿曲面相互垂直的3个方向(x、y、厚度方向)依次布点粘贴，双曲面上、下表面各粘贴4个光栅，厚度方向布放粘贴1个光栅，总计9个光栅，光栅长度为5 mm。为了避免环境因素的变化影响光纤波长的变化，设置1个校准光栅用于环境补偿，如图2所示。环境补偿光栅悬空放置，使其自身波长变化仅受环境变化的影响。

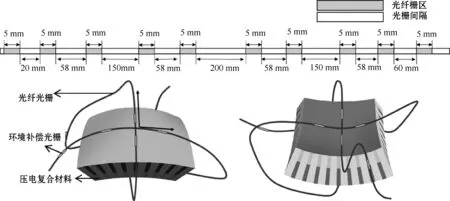
图2 光纤光栅设计及布线粘贴示意

测试系统包括光纤解调仪、高低温试验箱、阻抗分析仪及计算机。实验选用外径为50 mm、内径为45 mm、厚度为5 mm的双曲面压电复合材料进行测试。实验时先在双曲面压电复合材料试样的边缘焊接引线，再将光纤光栅粘贴布线至试样的表面，然后将试样放入高低温试验箱中，导线和光纤纤芯从高低温试验箱的出线孔引出，将光纤的接头连接到光纤解调仪，电极引线连接至阻抗分析仪，光纤解调仪和阻抗分析仪都与电脑相连，设置高低温试验箱从20 ℃开始逐渐降温至-40 ℃，然后逐渐升温至100 ℃。在20 ℃至-40 ℃降温过程中，每降温10 ℃保温10 min，光纤解调仪测试一组光纤波长数据，阻抗分析仪测试一组材料机电特性的数据；在-40 ℃至100 ℃升温过程中，每升高10 ℃保温10 min，光纤解调仪测试一组光纤波长数据，阻抗分析仪测试一组材料机电特性的数据。测试流程如图3所示。

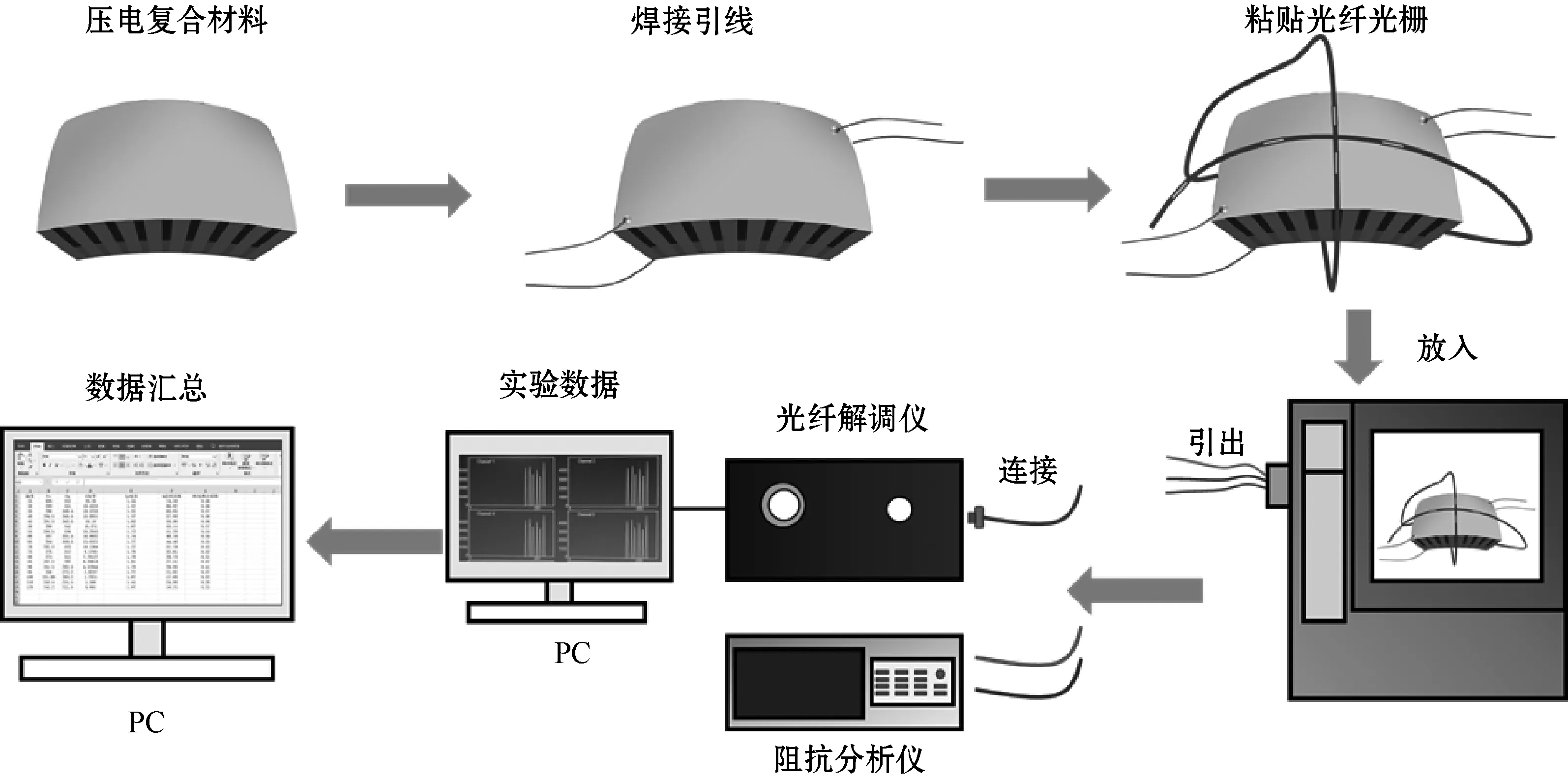
图3 实验测试步骤

2 实验结果与讨论

2.1 温度形变量

实验选用的双曲面压电复合材料试样的外径为50 mm，内径为45 mm，厚度为5 mm。以光纤光栅在20 ℃时测得的中心波长为基准，计算出其他各个测试点的中心波长变化量Δλ，将λ、Δλ代入式(4)～(7)可计算出每个方向的平均应变值εl。由图2光纤光栅的粘贴方式可知，将上表面x方向测得的平均应变ε上x乘以该方向对应的总弧长l上x，便可得到上表面x方向弧长形变L上x。即

L上x=ε上x×l上x

(9)

则双曲面压电复合材料的上表面y方向的曲面弧长形变也可按照上述方法进行计算获得，即

L上y=ε上y×l上y

(10)

同理，可得双曲面下表面x、y方向弧长形变的求解。取内外表面弧长的平均来表征曲面压电复合材料x、y方向上的曲面形变，则

(11)

(12)

厚度方向总形变Et可由厚度方向应变ε厚度方向乘以材料厚度t计算得到，即

Et=ε厚度方向×t

(13)

试样x、y两个方向的曲面形变与厚度方向形变随温度变化的曲线如图4～6所示。

图4 x方向曲面形变

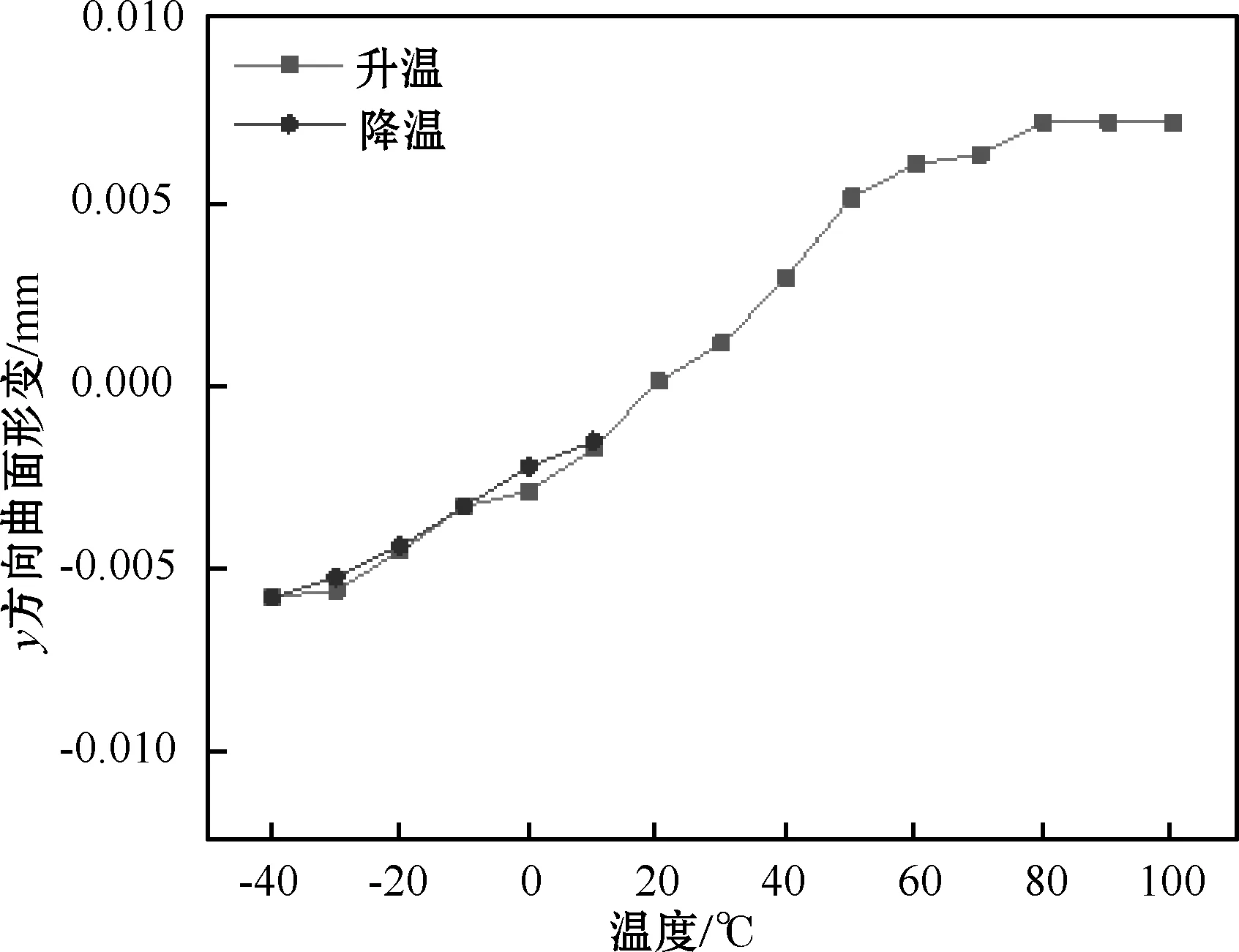
图5 y方向曲面形变

图6 厚度方向形变

从图4～6可以看出，双曲面压电复合材料x、y和厚度方向的形变在20～-40 ℃之间随温度的升降，变化趋势几乎相同，呈现可逆变化。在-40～100 ℃的温度范围内，x、y和厚度方向形变随温度升高先快速增大，而后缓慢上升。对数据进行线性拟合，可知在-40～60 ℃时，3个方向的形变变化率分别为2.86×10-4mm/℃、1.32×10-5mm/℃、2.54×10-4mm/℃；在60～100 ℃时，3个方向的形变变化率分别为2.36×10-5mm/℃、4.35×10-5mm/℃、1.84×10-6mm/℃。出现这种变化是由于双曲面型压电复合材料内部聚合物相材料在室温下固化成型，当温度从20 ℃升温至60 ℃时，内部填充聚合物继续固化，变得交联紧密，压电复合材料形变变化率增加。当温度大于60 ℃并继续升高时，由于内部填充聚合物完全固化，受温度影响形变量增幅减小，压电复合材料形变逐步趋于稳定。

2.2 谐振频率及频率常数相对变化率

压电复合材料的频率常数是指压电体的谐振频率f与该频率的主振动方向的几何尺寸的乘积：

Nf=f×t

(14)

在某温度T下，当温度变化ΔT时，谐振频率由fT变为fT+ΔT，则谐振频率相对变化率为

(15)

频率常数相对变化率为

δNf=Tf×(t+ET)

(16)

式中ET为温度T时复合材料厚度方向的形变量。

在计算频率常数相对变化率时，取20 ℃时的频率常数为参考值，将测量得到的压电复合材料厚度方向形变代入式(15)～(16)，可计算得出材料频率常数的相对变化率。双曲面压电复合材料谐振频率和频率常数相对变化率随温度变化的曲线如图7～8所示。

图7 谐振频率-温度曲线

图8 频率常数相对变化率-温度曲线

从图7～8可知，双曲面压电复合材料的谐振频率和频率常数相对变化率在20～-40 ℃之间，随温度的升降变化趋势几乎相同，呈现可逆变化。在-40～100 ℃范围内，谐振频率随温度的升高而降低，对数据进行线性拟合，可知下降速度为0.187 kHz/℃，在100℃时，已下降约18 kHz；在20～-40℃降温过程中，频率常数相对变化率随温度的升高而降低，下降速度为1.81×10-2%/℃。在-40 ℃～100 ℃的升温过程中，频率常数相对变化率先随温度升高而下降，进行线性拟合，可知下降速度为1.95×10-2%/℃，后又随温度升高而增大，增大速度为4.47×10-2%/℃。

2.3 机电耦合系数

机电耦合系数是表征压电材料机电转换效率的参数，其值越大，材料的机电转换效率就越高。较高的机电耦合系数能够有效提高换能器的发送响应，增大声呐系统的探测距离。利用阻抗分析仪测得复合材料的串联谐振频率fs及并联谐振频率fp，进而可计算出复合材料厚度振动机电耦合系数kt：

(17)

实验中，高低温试验箱调节测试温度，将测试得到的fs及fp代入式(17)，便可得到机电耦合系数随温度变化规律。压电复合材料的相对介电常数εr可通过测量样品在低频时的电容，并利用式(18)计算得到。复合材料的电容可使用阻抗分析仪直接测量获得，测试频率通常取1 kHz。

(18)

式中：C0为样品的准静态电容，单位F；t为样品厚度，单位m；A为样品的电极面面积，单位m2；ε0为真空中的介电常数，ε0=8.85×10-12F/m。复合材料试样的机电耦合系数和相对介电常数随温度变化的曲线如图9～10所示。

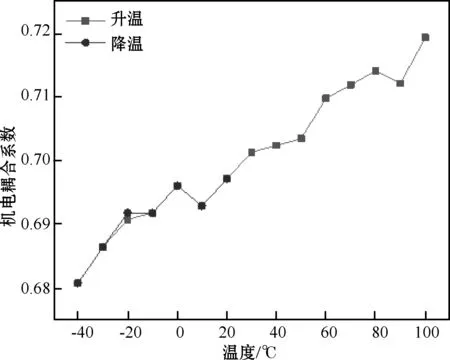
图9 机电耦合系数-温度曲线

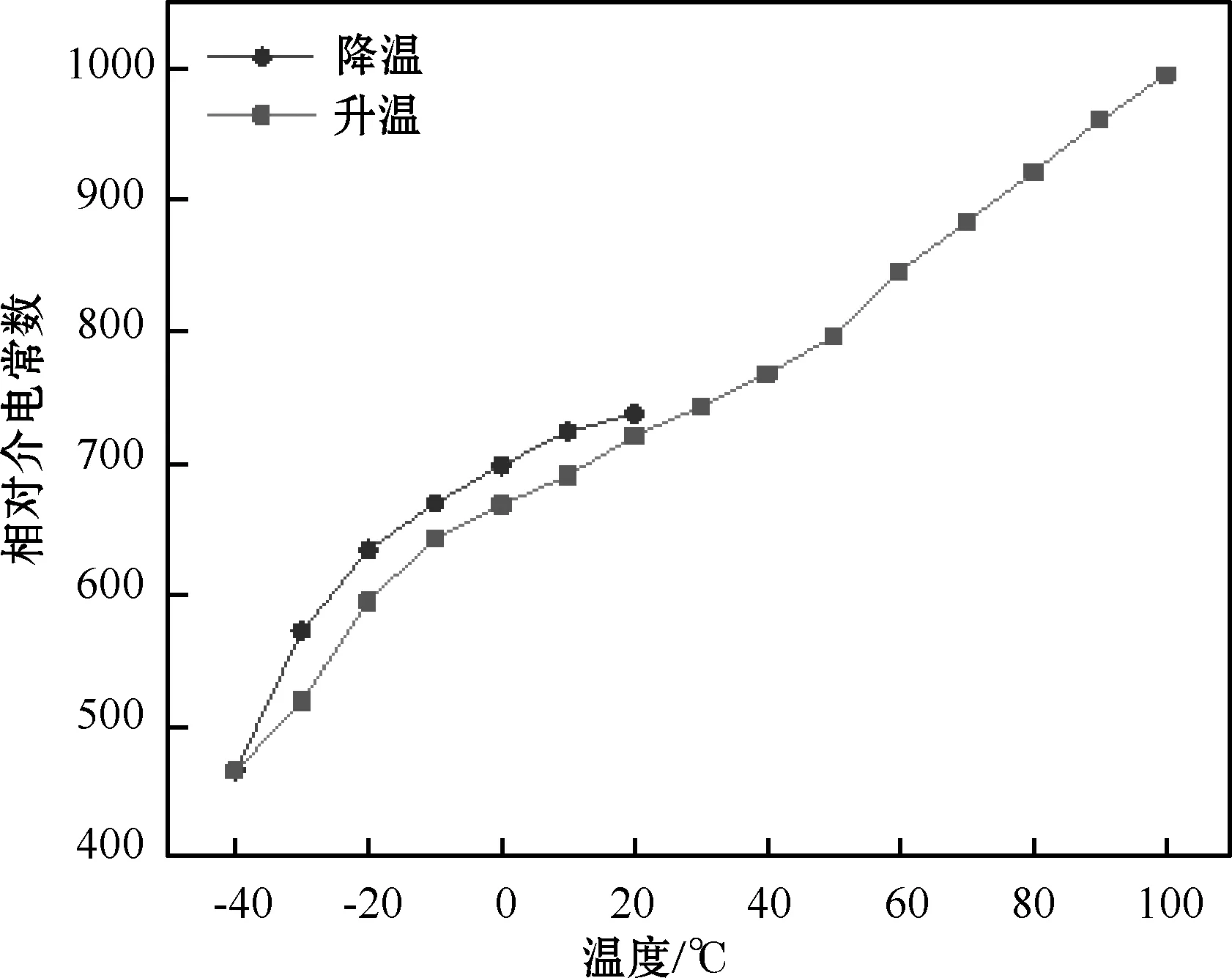
图10 相对介电常数-温度曲线

从图9、10可知，双曲面压电复合材料的机电耦合系数与相对介电常数在20～-40 ℃之间，随温度的升降变化趋势几乎相同，呈现可逆变化。在20～-40 ℃的降温过程中，JP机电耦合系数和相对介电常数随着温度的降低而下降，在-40 ℃时分别达到了0.681和466；在-40～100 ℃升温过程中，机电耦合系数与相对介电常数随温度升高而升高，在100 ℃时分别达到了0.72和996。

3 结束语

本文对双曲面压电复合材料温度稳定性进行了研究，利用光纤光栅法实现了对双曲面压电复合材料的形变测量。建立了双曲面压电复合材料温度形变定量测试系统，测试了在-40～100 ℃范围内双曲面压电复合材料的形变和机电性能，一定程度上解决了双曲面压电复合材料温度形变精确定量测试问题。研究结果表明：双曲面压电复合材料3个方向的形变、谐振频率、频率常数相对变化率、机电耦合系数和相对介电常数在20～-40 ℃之间，随温度的升降变化趋势几乎相同，呈现可逆变化。在-40～100 ℃的温度范围内，x、y和厚度方向形变随温度升高先快速增大，而后缓慢上升；谐振频率随温度的升高而降低，在100 ℃时已下降约18 kHz；频率常数相对变化率先随温度升高而下降，20 ℃后随温度升高而升高；机电耦合系数和相对介电常数随着温度的降低而减小，随温度的升高而增大。