热敏感流体空化数值模拟及流动特性分析

杨其文，张炜，李晓俊，陈峰，朱祖超

(1.中石化洛阳工程有限公司，河南 洛阳 471003；2.浙江理工大学浙江省流体传输技术研究重点实验室，浙江 杭州 310018；3.浙江机电职业技术学院机械技术系，浙江 杭州 310053)

空化通常出现在液体局部静压低于当地热力学状态下的饱和蒸汽压而发生气化的过程，是一种复杂的相变现象[1].通常对于热力学不敏感的流体(例如常温下的水)，空化被假设为等温过程[2].然而，对于热力学敏感流体(例如低温流体，氟化酮以及高温下的水)，这种等温假设是无效的[3].由于气液密度较小，当气化形成同样大小的空腔时，热力学敏感流体需要比热力学不敏感流体气化更多的液体.

低温离心泵通常承担所在系统“心脏”的作用，涉及的空化问题直接决定低温流体装备及系统的稳定性.由于流道结构复杂、影响因素繁多，低温离心泵的空化是困扰所在行业发展的“卡脖子”难题，它不仅影响低温泵的水动力性能，同时造成高幅度的结构振荡.美国Fastrac火箭和日本H-ⅡA火箭[4]在研制过程中均出现了因诱导轮低温空化造成的破坏.

与常温水介质空化相比，热敏流体空化的本质区别是流体介质的物理属性随温度变化敏感.SARSDY等[5]通过试验首次发现水和氟利昂中空化的差异.发现当空化在水中发生时，气液界面清晰透明，然而氟利昂发生空化时，空泡界面模糊，呈泡雾状.HORD[6]在NASA的资助下进行了一系列有关水翼、文丘里管和回转体的热敏空化试验.试验数据常常被用来验证数值模拟的有效性.KELLY等[7]通过高速摄影技术研究了不同空化数、不同入口温度以及不同攻角下氟化酮绕NACA 0015水翼的非稳态空化特征，并记录了水翼表面的压力数据，但并未给出温度数据.LE等[8]使用修正的Merkle空化模型数值研究了液氢和液氮的空化流动，并考虑了可压缩性.LIANG等[9]基于输运方程的修正空化模型数值研究了不同温度的水绕NACA 0015水翼的空化流动.SUN等[10]数值研究了氟化酮和液氮绕NACA 0015水翼空化流动.发现温度分布与空腔的演化有关，而且对于同样的空化数，液氮的温降更明显.朱佳凯等[11]通过试验和数值模拟观察了液氮在文氏管和水翼中的空化特性，测量了空化过程的流量、温度及压力的动态变化，证实了压比大于2.23时，空化溃灭产生的压力波为空化脱落的主要机理.

文中目的是验证修正的ZGB空化模型在热敏空泡流中的有效性，研究氟化酮空化流动的热力学效应以及动态脱落过程，并以此揭示热力学空化流动特征.

1 数学模型及数值方法

1.1 控制方程

热力学空化流动是一种复杂的多相流问题.考虑到计算资源和精度，均匀混合流模型是一种比较合理的选择.均匀混合模型是将气相和液相视为一种均匀混合物.两相共用一套控制方程，为了降低计算资源，两相之间的相互作用被忽略.质量方程、动量方程、能量方程和输运方程的计算公式为

(1)

(2)

(3)

(4)

式中：ρm，u，p和μm分别为混合密度、速度、压强和混合层流黏度；i，j，k分别为直角坐标系中的x，y，z方向；T，C，K和L分别为温度、比热容、热导率和气化潜热.

它们的定义式如下：

ρm=αvρv+(1-αv)ρl,

μm=αvμv+(1-αv)μl,

(5)

式中：下标v和l分别表示气相和液相.

1.2 基于输运方程的空化模型

输运方程的源项由Rayleigh-Plesset方程推导得出，即

(6)

式中：RB为单个球形气泡半径；S0为表面张力；pv为当地温度下的饱和蒸汽压.忽略黏性项、二阶导数项和表面张力项，可以得到气泡半径对时间求导项：

(7)

式(7)考虑了压力变化对气泡大小的影响，但是忽略了温度变化对气泡大小的影响.对于热力学敏感流体(如液氢、液氮和氟化酮等)而言，其物质属性对温度的变化非常敏感.气泡壁面的自然对流引起的温差计算公式为

(8)

式中：hb为对流换热系数.

进一步推导得出：

(9)

其中，

(10)

式中：C0为经验系数；热扩散系数λl=Kl/ρlCl.

将式(10)代入式(9)中可得：

(11)

重新修正ZGB空化模型，可以得出考虑热力学效应的空化模型为

(12)

(13)

式中：RB=1.0×10-6m，经验系数Fvap和Fcond对热力学空化流动数值模拟的结果产生重要影响.SUN等[12]重新修正了该经验系数，发现Fvap=5.0和Fcond=0.001能够较好地预测温度和压强，文中数值模拟将使用该经验系数.

试验表明湍流对空化流动产生重要影响，通常使用湍动能k和混合密度ρm来修正饱和蒸汽压，修正的饱和蒸汽压公式为

ptur=0.39kρm,

(14)

(15)

式中：pv(T)为饱和蒸汽压，是温度的函数.

2 数值计算与验证

2.1 绕二维水翼稳态空化流动的数值验证

采用文献[6]在NASA的资助下进行的热敏空化试验来验证数值计算方法的有效性.试验模型是一个安装在截面为方形的水洞中且前缘半径为3.96 mm的半球头型水翼.5个温度传感器和压力传感器分别安装在水翼的上表面.由于水翼的上下表面对称，所以只选取其中的一半作为计算域.二维的计算域边界条件如图1所示.

图1 计算域和边界条件

水翼表面设置为绝热，自由滑移.入口的速度和温度根据试验数据设定，出口压强需要进行多次调整，使计算得到的入口压强与试验数据保持一致.对流项设置为高分辨率格式.

在水翼表面附近进行网格加密，并设计6套网格验证网格无关性，网格1的单元总数为5 641，网格2的单元总数为10 205，网格3的单元总数为25 325，网格4的单元总数为50 423，网格5的单元总数为83 505，网格6的单元总数为128 561.图2为6套网格的无关性分析，基于6套网格的计算结果差别不大，综合考虑计算精度和计算时间，后续计算采用网格3(单元总数为25 325).

图2 模拟压力系数与试验数据对比

文献[6]试验中选择的293F工况作为参考数据，根据试验参数，设置进口速度为23.9 m/s，温度为77.9 K.图3为ZGB模型和文中修正的ZGB空化模型(MZGB模型)的计算结果对比.

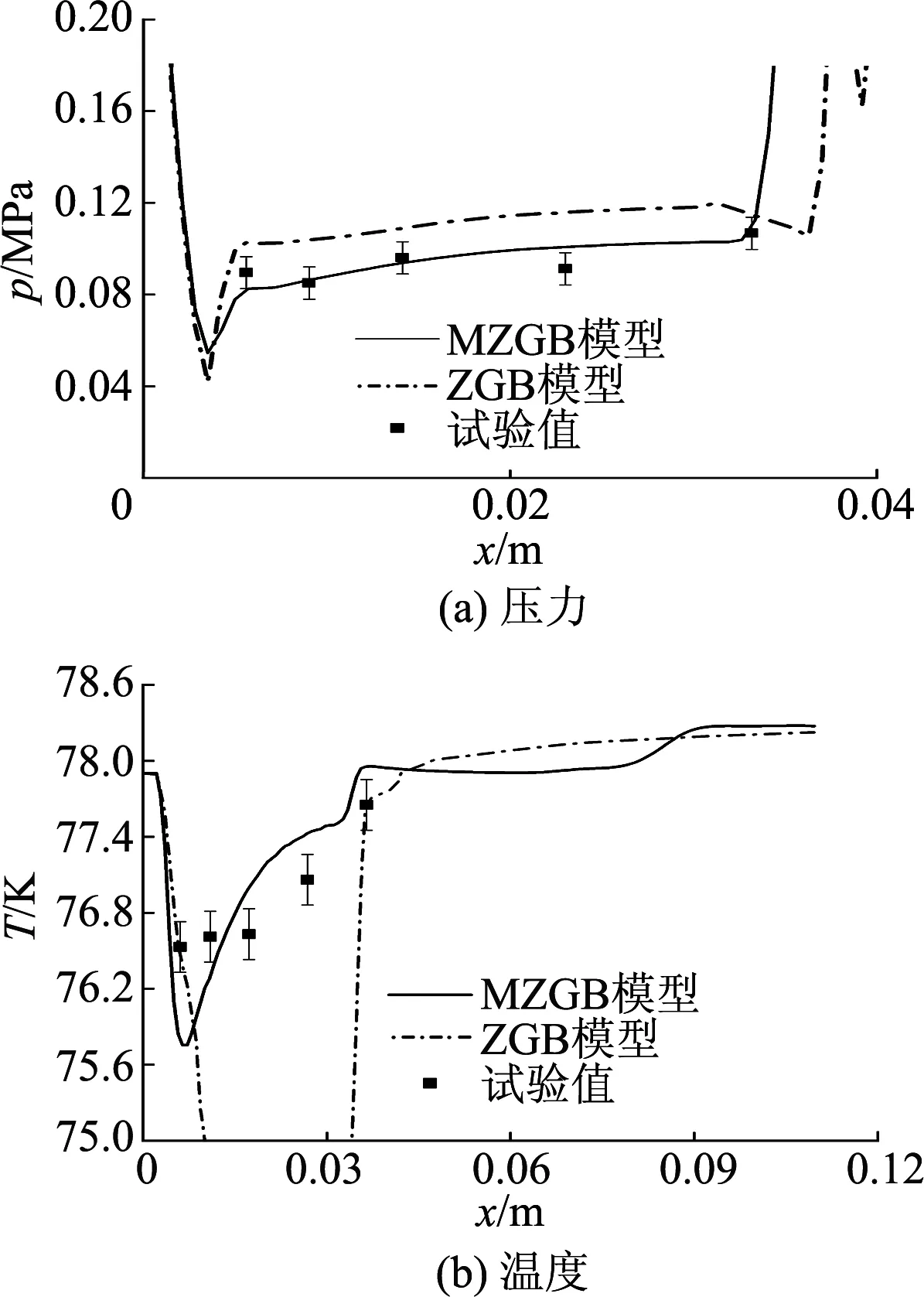
图3 数值计算得到的压力和温度与试验数据对比

由图3可知，在水翼随边附近出现了较大的温降和压降.随着流动往下游移动，由于气体凝结的缘故，温降和压降逐渐减小.这表明水翼导边附近气化吸热导致了明显的热效应出现.从图中对比结果可知，MZGB计算得到的结果与试验数据更加接近.随着入口温度的降低，空化强度逐渐增加，空腔尾部的闭合区域沿着水翼表面向下游延伸.空化的传质过程能够影响局部流场和温度场.由该图可以发现MZGB模型在处理热敏空化流动方面具有优势，能够较好地预测水翼表面温度和压力的分布.需要注意的是在空腔尾部的闭合区域预测的压力与试验数据存在一定程度的差别，这可能是出口处的阻塞效应引起.

2.2 绕三维水翼非稳态空化流动的数值验证

热敏流体空化流动的计算域与文献[7]的试验装置一致，如图4所示.

图4 几何模型及边界条件

图5 水翼表面及附近的网格

网格节点总数为2 412 720.对流项采用高分辨率格式，瞬态项采用二阶向后欧拉格式.为了平衡计算资源和计算精度，将RMS的残差设置为10-4.研究中，将稳态的无空化流动计算结果作为非稳态空化流动的初始计算文件，时间步长设置为Δt=Tr/100=6.8×10-5s(Tr=c/u∞).

图6以气体体积分数10%的等值面表示空腔形状，并选择4个典型时刻的图片与Kelly试验观察的照片做比较.从中可以看出该模型可以合理地预测到试验过程中三维水翼附近空腔的脱落及其演化过程.这表明该数值方法可以模拟出热力学空化流动特征.

图6 数值模拟得到的空腔形状与试验对比

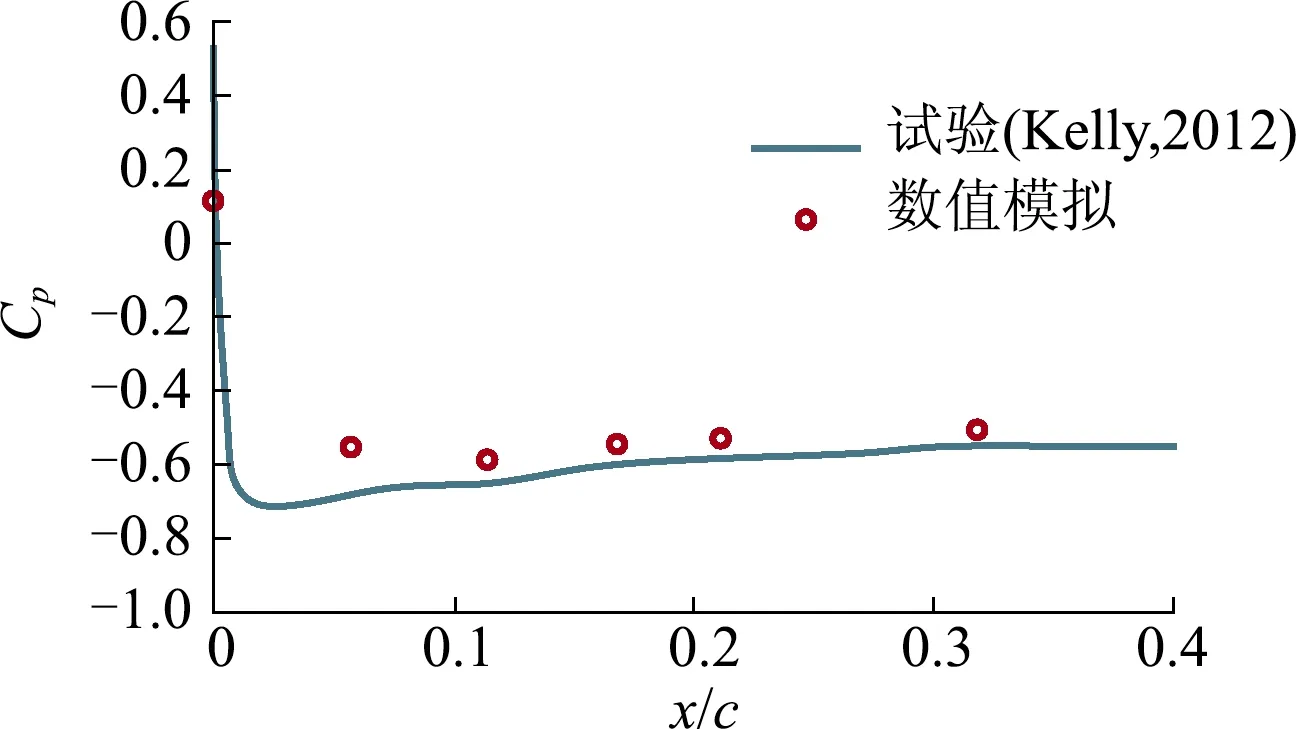
图7 水翼吸力面压力系数分布的对比

2.3 热敏流体空化脱落的动态特征

由图6，7可知，文中三维水翼非稳态空化流动的仿真结果与试验数据基本一致.为了描述热力学空化流动的动态特征，图8显示了空腔总体积随时间的变化过程，其计算公式为

(16)

式中：N为计算域中控制单元的总数目；αi为每个控制单元中气体的体积分数；Vi为每个控制单元的体积.

图8说明了气体总体积随时间的变化过程是准周期的.选取一个典型周期中8个时刻来显示空腔的形成、发展、脱落和溃灭过程，并以气体体积分数为10%的等值面.图9同时显示了各时刻中截面的温度云图.从图中可知，空腔区域的温度要比周围液体的温度低，这是空化时出现的气化吸热导致的.若将Tref定义为图9中典型周期的时间，则可对非稳态热力学空化流动进行以下描述：① 从0.125Tref到0.375Tref时刻，由于回射流的作用，水翼吸力面上的附着空腔脱落，并被主流输运到下游变成流动更加紊乱的云空化；② 与此同时，水翼前缘的附着空腔开始形成，并向水翼尾部生长；③ 从0.500Tref到0.625Tref时刻，脱落的云空化溃灭，产生瞬间高压，并以压力波的形式向四周传播；④ 从0.750Tref到1.000Tref时刻，回射流开始形成，并开始诱导附着空腔脱落.

图8 空腔总体积的变化

该8个时刻基于Ω方法识别的旋涡等值面，其定义式如下

(17)

(18)

(19)

(20)

式中：A为对称矩阵；B为反对称矩阵；ζ为一个避免分母为0而设置的很小的正数.

LIU等[13]认为Ω=0.52的等值面能够较好地识别旋涡的表面.从图9中看到Ω准则可以清楚地显示出许多发夹涡结构，Ω的等值面与脱落的空腔形状相似，这表明脱落的空腔区域中呈现大规模的旋涡运动，这与早期试验观察的结果一致[14].值得注意的是，在水翼的尾缘附近，Ω的等值面比空腔形状更复杂.这是由于附着的空腔脱落形成云空化后，随即被卷向下游.当它被输运到高压区域，其迅速溃灭形成大量的微型气泡.在此过程中，Ω的等值面不但没有变小，反而变更大更加复杂了，并且被主流输运到下游.这说明空腔的脱落和溃灭促进了旋涡结构的形成.

图9 非定常热力学空化周期性发展过程

图10展现了一个典型周期内的水翼截面处预测温降与B因子预测温降的对比.

图10 一个典型周期内水翼中截面的温降

利用B因子对热敏空化流的热效应进行分析，其计算公式为

(21)

从图10中可以看出，B因子能够有效地预测大部分区域的温降，与预测值十分符合.但图中仍有2个地方存在明显的误差，其中一个是B因子无法预测由于液化放热导致的温升，已在图中用绿线标出.水翼前缘由于空腔的生长，存在一个明显的温降，但B因子理论过度预测了该温降，已在图中用粉线标出.整体上，B因子还是能够有效地预测空化区域内的温降.

3 结 论

1)基于输运方程的修正空化模型结合混合湍流模型能够较合理的预测流动细节，模拟结果与试验数据基本吻合.

2)回射流、涡旋与流动分离之间有很强的关联性.黏性和逆压梯度诱导回射流的形成.当回射流与主流相互作用时，将诱导涡旋的形成和脱落.形成的涡旋反过来又影响流场的结构，并常常伴随着流动分离的出现.

3)Ω的等值面与脱落的空腔形状相似，这表明脱落的空腔区域中呈现大规模的旋涡运动.此外，在水翼的尾缘附近，Ω的等值面比空腔形状更复杂，这说明空腔的脱落和溃灭促进了旋涡结构的形成.

4)在空化区域，水翼壁面存在明显的温降，B因子能够有效地预测腔内温降，但仍存在过度预测.