海水淡化能量回收透平水力模型优化设计

张德胜，祁炳，赵睿杰，张奇

(江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013)

海水淡化能量回收一体机是高压离心泵和透平式能量回收装置一体化的水力机械.一体机通过透平式能量回收装置将未透过反渗透膜的浓盐水高压能转化成机械能，驱动主轴旋转带动另一侧高压泵，从而回收反渗透膜后高压浓盐水的能量，被广泛应用于中小型反渗透海水淡化系统.

目前，关于能量回收透平的研究主要集中在泵作透平选型、运行稳定性与性能提高等3个方面[1].SINGH等[2-3]提出了一种离心泵作透平的优化方法，该方法可用于预测离心泵作透平工况的性能以及离心泵作透平的选型，并通过试验进行了验证.DERAKSHAN等[4-5]利用试验数据，根据离心泵的水力特性，推导出预测离心泵作为透平工作的最佳效率点的关系式，并通过试验证明了该方法的有效性.NAUTIYAL等[6]根据已有的试验结果，利用液力透平在泵模式下的最佳效率和比转数建立了新的关联关系.史广泰等[7]分析了叶轮内部相对环流流动的特征，提出了 3 种计算离心泵反转作液力透平叶轮出口滑移系数的方法，得到了相应的叶轮出口滑移系数解析计算公式.

近年来，随着计算流体动力学的日益改进和完善，数值计算方法已被广泛应用于透平性能的预测.JAIN等[8]研究了叶片修圆及叶轮直径对离心泵反转作透平的性能影响，发现对透平叶片进口边修圆及前、后盖板外缘修圆，可使透平效率提高1%～4%.苗森春等[9]采用使叶片型线参数化、神经网络与遗传算法对一液力透平进行叶片型线的优化改进，发现该方法对改进叶片型线具有一定的可行性.YANG等[10]提出在最优效率点泵和透平的流量系数和扬程系数之间的关系，可以根据泵的性能参数更加准确地预测透平最优效率点的参数.宁廷州等[11]以锯末含水率、成型模具长径比和主轴转速为试验因素，以成型颗粒密度和成型机生产率为试验指标，基于试验设计方法BBD(Box-Behnken Design)对试验数据进行处理和分析，建立了试验因素对试验指标的回归方程.

基于试验设计方法和响应面分析方法在海水淡化能量回收透平水力模型研究方面较少涉及，文中基于试验设计方法和响应面分析方法建立回归方程，对海水淡化能量回收透平的水力模型进行优化分析，为泵作透平的水力优化设计提供参考.

1 透平模型及数值计算设置

1.1 能量回收透平物理模型

图1为高压泵与透平式能量回收一体机结构简图.选用一台比转数ns=98的带直锥型蜗壳的单级单吸离心泵作透平，其基本设计参数分别为设计流量Qd=50.9 m3/h，进口压力pin=5.0 MPa，转速n=20 000 r/min.

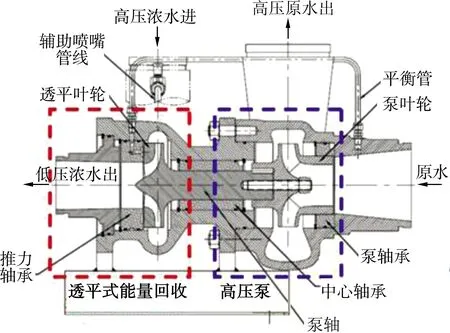
图1 高压泵与透平能量回收一体机结构图

1.2 计算域模型及网格无关性验证

透平的计算域包括进水管、叶轮、前后腔体、蜗壳(含出口延伸段)等，采用六面体网格对模型进行网格划分，计算域模型如图2所示.

图2 计算域模型

进行网格无关性检测，发现当网格数超过1.8×106时，计算效率基本保持不变.本次计算模型的总网格单元数为2 270 068，节点数为2 403 320.

1.3 数值计算及试验验证

应用计算流体动力学软件ANSYS-CFX对离心泵作透平内部流场进行计算，选择模型泵进口为质量流量边界条件，出口边界条件设为自由出流，参考压力为101.325 kPa.压力与速度的耦合方式采用SIMPLE算法，计算收敛精度设为1.0×10-4，湍流模型采用k-ε模型，输送介质为常温清水.通过调节进口质量流量大小改变透平的运行工况，从而计算得到透平的外特性曲线.

为了验证数值计算方法的可靠性，对该样机在泵工况时进行不同流量工况下的性能进行试验，将样机泵外特性的数值计算结果与试验结果进行对比如图3所示.

图3 样机泵试验和数值计算结果对比

由图3可以看出：该样机泵数值计算和试验的扬程、轴功率和效率曲线变化趋势基本一致，数值计算的扬程整体略低于试验值，而数值计算的效率略高于试验值，这可能是由于数值计算时忽略了间隙泄漏和圆盘摩擦损失以及在试验加工零件时与建模产生的误差造成的；泵最高效率点的流量均在120 m3/h，此时计算效率比试验效率高2.7%，计算扬程比试验扬程低2.1%，误差较小，这表明文中所采用的数值计算方法是可靠的.

2 透平叶轮优化设计方案

2.1 性能指标

液力透平的扬程和效率是衡量透平水力性能优劣的重要指标.液力透平的扬程H指单位重量流体经透平所减少的能量，其计算公式为

(1)

式中：pin为透平入口总压；pout为透平出口总压；ρ为水的密度.

液力透平的效率η指透平所获得的轴功率与输入功率之比，其计算公式为

(2)

式中：M为透平转子的转矩；ω为透平转子的转速；Q为透平的流量；H为透平的扬程.

2.2 试验设计

采用BBD试验设计的方法，选择叶片进口角β1、叶片出口角β2和叶片数Z为试验因素，以透平的水头和效率为试验指标，并以-1，0，1分别代表试验因素水平，如表1所示.

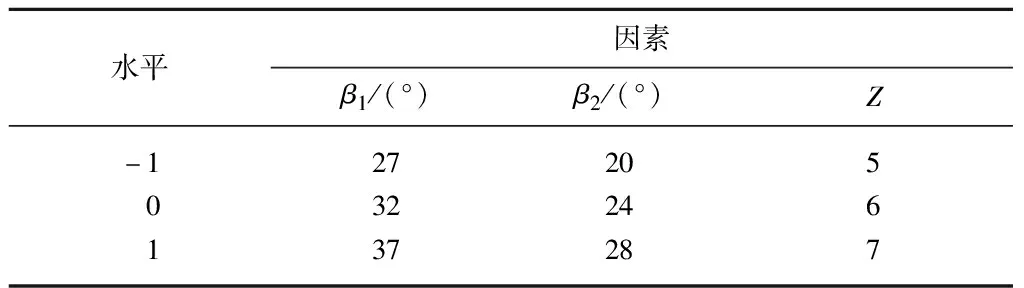
表1 试验三因素三水平

3 试验结果及分析

采用Design-Expert分析软件，基于BBD试验设计方法，共形成17组试验方案，采用ANSYS-CFX软件对上述17组试验方案分别进行计算，结果如表2所示.表中X1，X2，X3分别表示叶片出口角、进口角和叶片数；Y1，Y2分别表示透平的水头和效率.

表2 试验方案与性能计算结果

在对重新组合的17组叶轮模型进行数值计算过程中，保持蜗壳及腔体几何参数不变，以及同样的湍流模型和边界条件.从计算结果可以看出，叶片出口角、进口角和叶片数对透平性能有非常明显的影响，不同的参数组合也会得到不同的性能指标.

3.1 回归方程的建立

3.1.1 透平扬程回归方程

透平扬程的回归方程为

(3)

透平扬程的方差分析如表3所示，可以看出，模型P值等于0.000 3(小于0.001 0)，模型回归方程具有统计学意义，且该模型R2修正值为0.996 5(大于0.800 0)，说明该方程与试验拟合良好，试验因素与试验指标—扬程之间的关系具有统计学意义，该模型能够满足对透平扬程进行预测.

表3 透平扬程方差分析

3.1.2 透平效率回归方程

透平效率的回归方程为

η=83.08+0.063X1-0.67X2+1.94X3+0.22X1X2+

(4)

透平效率的方差分析如表4所示,可以看出，模型P值等于0.000 4(小于0.001 0)，模型回归方程具有统计学意义，而失拟项P值等于0.797 3(大于0.050 0)，不具有统计学意义，且该模型R2修正值为0.996 5(大于0.800 0)，说明该方程与试验拟合良好，试验因素与试验指标—效率之间的关系具有统计学意义，该模型能够满足对透平效率进行预测.

表4 透平效率方差分析

3.2 各试验因素对试验指标影响程度分析

根据F检验数值可以判断各试验因素对试验指标的贡献率.各试验因素对各试验指标的贡献率如表5所示，可以看出，叶片数对透平扬程和效率的贡献率均最大，叶片出口角对透平扬程的贡献率比叶片进口角大，而叶片进口角对透平效率的贡献率比叶片出口角大.

表5 试验因素对透平性能指标的贡献率

3.3 试验因素交互作用对试验指标的影响

基于Design-Expert数据分析得到叶片不同参数交互作用对透平扬程和效率的响应面图，进而可以找出参数对透平性能指标的影响规律，从而为透平叶轮性能参数的优化提供理论依据.

3.3.1 叶片进口角和出口角交互作用对透平性能指标的影响

图4为叶片进口角和出口角对透平性能交互影响的响应面图.

图4 叶片进口角和出口角对透平性能的影响

由图4可以看出：当透平叶片数固定在某一水平，随着叶片进口角的增大，透平的扬程随之增大，而透平效率先增大后减小；随着叶片出口角的增大，透平的扬程逐渐减小，而透平的效率呈先增大后减小的趋势，出口角对效率的影响大于对透平扬程的影响；当透平叶片进口角为27°～33°，叶片出口角为22°～26°时，透平扬程可达505 m，效率可达82.5%.

3.3.2 叶片进口角和叶片数交互作用对透平性能指标的影响

图5为叶片进口角和叶片数对透平性能交互影响的响应面图.

图5 叶片进口角和叶片数对透平性能的影响

由图5可以看出：当叶片出口角一定时，随着叶片数的增大，透平的扬程和效率均呈上升趋势，其中透平的效率上升趋势明显，说明叶片数对透平性能的影响非常明显；随着叶片进口角的增大，透平的扬程也逐渐增大，透平的效率先增大后减小，但影响效果均比叶片数对透平性能影响的效果弱；当叶片数为7，叶片进口角为27°～33°时，透平的扬程大于505 m，透平效率大于83%.

3.3.3 叶片出口角和叶片数交互作用对透平性能指标的影响

图6为叶片出口角和叶片数交互作用对透平性能影响的响应面图，可以看出：透平叶片数对透平扬程和效率的影响均比透平出口角大，当透平叶片数为7，叶片出口角为22°～26°时，透平的扬程大于505 m，透平的效率大于83%.

图6 叶片出口角和叶片数对透平性能的影响

3.4 成型参数优化

基于上述分析，采用Design-Expert对叶片进口角、出口角和叶片数进行参数优化，相比透平的效率和扬程，在透平扬程满足设计要求的前提下，更看重效率的提升.

因此，给透平扬程赋0.3的权重，给透平效率赋0.7的权重，在透平进口角为27°～33°，出口角为22°～26°，叶片数为6和7的约束条件下，设定透平扬程和效率最大化，得到的优化结果为进口角为28.8°，出口角为23.4°，叶片数为7，此时透平的性能达到最优.

3.5 性能对比分析

图7为原型透平和优化后透平数值计算外特性结果，可以看出：2台透平的外特性变化趋势基本一致，透平的扬程和轴功率随流量的增大而增大，透平的效率随流量的增大先增大后减小，效率在0.8Qd处达到最大，说明透平的设计参数更匹配偏小流量工况运行；在相同工况下，原型透平的扬程和轴功率比优化透平的低；在0.5Qd～0.7Qd工况，原型透平的效率比优化透平的高，在0.8Qd～1.2Qd工况，优化透平的扬程和效率均比原型透平的高；在设计工况点，优化透平的扬程比原型透平的高6 m，优化透平的效率比原型透平提高0.8%.

图7 优化前后透平外特性对比

4 结 论

根据海水淡化一体机透平的设计参数，建立其计算模型，应用ANSYS数值计算软件和Design-Expert分析软件对计算模型进行研究，经过选型、相似换算、透平叶片参数优化等，得到如下结论：

1)选型泵经数值计算和试验测量得到的扬程、轴功率和效率曲线变化趋势基本一致，且误差较小，说明该数值计算方法对该泵内部流场的数值模拟具有一定的可信度.

2)通过对透平叶轮叶片几何参数的优化，发现叶片数对透平水头和效率的贡献率均最大，叶片出口角对透平水头的贡献率比叶片进口角大，而叶片进口角对透平效率的贡献率比叶片出口角大.

3)当透平的叶片进口角为28.8°，叶片出口角为23.4°，叶片数为7时，透平的性能达到最优.在0.8Qd～1.2Qd工况下，优化透平的水头和效率均比原型透平的高.在设计工况点，优化透平的扬程比原型透平的高6 m，优化透平的效率比原型透平提高0.8%.