基于分数阶功率谱熵的未知水声脉冲信号检测方法

夏文杰，黎 鑫，曹伟浩，尹锡帆

(1. 国家海洋技术中心漳州基地筹建办公室，福建厦门361001；2. 国防科技大学气象海洋学院，江苏南京210000；3. 海军工程大学电子工程学院，湖北武汉430000)

0 引 言

侦察声呐作用距离比对方主动声呐作用距离远，对远程警戒有重要意义，侦察的对象常是水中平台辐射的主动脉冲信号。主动声呐典型的发射脉冲[1]有：单频(Continuous Wave, CW)信号和调频(Frequency Modulation, FM)信号，FM信号主要为线性调频(Linear Frequency Modulation, LFM)和双曲调频(Hyperbolic Frequency Modulation, HFM)形式。

针对无先验知识的信号检测问题，目前主要有能量检测器、幂律检测器、基于分数阶傅里叶变换(Fractional Fourier Transform, FRFT)的检测和功率谱熵检测器等方法。能量检测器[2]是高斯背景中检测高斯信号的最佳检测器，但脉冲信号有其特征，不属于随机信号范畴，难以在低信噪比下检测信号。幂律检测器[3]是一种非高斯背景下检测随机信号的非参数方法，可看作高次幂的能量检测器，检测性能较优于前者，但在海洋色噪声背景下性能低。基于FRFT检测的方法较多[4-5]，其中短时分数傅里叶变换(Short Time-Fractional Fourier Transform, ST-FRFT)检测方法[5]结合时频分析和信号能量聚集性质，实现了水声脉冲信号的截获检测。功率谱熵检测算法利用信号与噪声的功率谱熵差异，判断是否存在信号，已应用于各类信号检测领域，检测器对未知CW信号有较好的检测性能，但是对FM信号的检测性能劣于前者[6]。针对这些不足，结合FRFT能聚集FM信号能量的性质与功率谱熵检测方法，提出了一种分数阶功率谱的非合作检测器，利用脉冲信号与噪声的统计量差异，实现对水声脉冲信号的检测。理论分析和仿真实验验证了FRFT对FM信号的能量聚集效果和检测性能。海试结果表明，检测器能在低信噪比下捕获主动声呐广泛使用的CW和FM水声脉冲信号，可实现信号的统一自动检测。

1 功率谱熵检测器

信息熵是描述系统信息量的物理量，系统有序程度越高，熵值就越小，信息量就越大，反之系统无序，熵值大，信息量小。未知水声脉冲信号检测从频域角度定义信息熵，可度量接收信号在频域上的复杂程度，利用功率谱熵表征和提取脉冲信号与背景噪声的不确定性差异，实现信号检测。具体地，若接收数据中不含信号，其功率谱熵值较大；否则功率谱熵值较小。将未知脉冲信号检测看成二元假设检验问题：

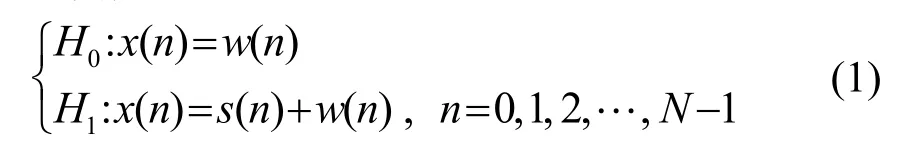
式中：x(n)表示接收数据，s(n)为信号，w(n)为加性噪声，N为样本长度。

功率谱熵检测的步骤如下[7]：

(1) 利用离散傅里叶变换得到信号归一化的功率谱密度估计：

式中：X(k)为信号的离散傅里叶变换，p(k)表示第k个功率谱值占总功率谱的值。

(2) 计算的相应功率谱熵H，作为检测统计量T：

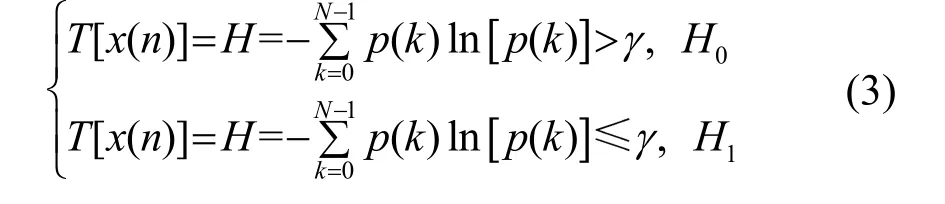
式中：γ为检测门限。若检测统计量T小于检测门限，备择假设成立，认为接收数据中存在脉冲信号。

功率谱熵检测器对未知CW脉冲信号有较好的检测性能，但由于FM信号的功率谱聚集性不强，导致检测器性能降低。而FRFT对于LFM信号，通过搜索到合适的旋转角度，理论上可得到一个冲激信号，信号能量由原先在频域内散布变换到新域内聚集；对于小曲率HFM信号，FRFT也有一定的聚集作用。因此，提出分数阶功率谱熵算法来提升对未知LFM和HFM脉冲信号的检测性能。

2 分数阶功率谱熵检测器

2.1 分数阶功率谱定义

分数阶傅里叶变换可将信号作任意角度α=πp/2的旋转，从线性积分的角度定义信号的p阶分数阶傅里叶变换[8]：

2.2 脉冲信号分数阶功率谱

常用的声呐脉冲有CW、LFM和HFM信号，复数表达式分别为[9-10]

式中：A为信号幅度；f0为中心频率；T为信号长度；k为线性调频率；K为双曲系数；t0为常数。

当k=0时，LFM信号即为CW信号，下面分析FM信号的分数阶功率谱聚集性。

2.2.1 LFM信号分数阶功率谱

仿真验证：LFM 信号中心频率f0=100.1 Hz，调制频率 k=50 Hz·s-1，幅度 A=1，采样频率fs=1024 Hz，点数N=1 024。图1(a)为p=1.031时的分数阶功率谱，图 1(b)为式(13)的理论计算结果，图1(c)为 p=1时的分数阶功率谱，即功率谱。验证了仿真结果和理论计算的一致性，FRFT对 LFM信号能量聚集强。

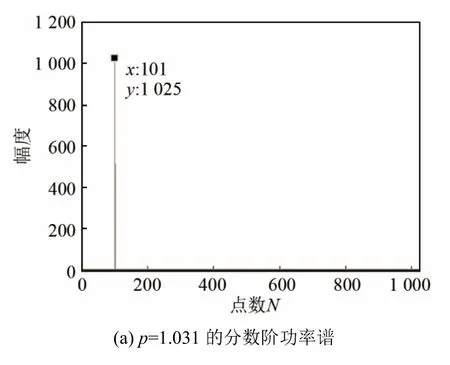
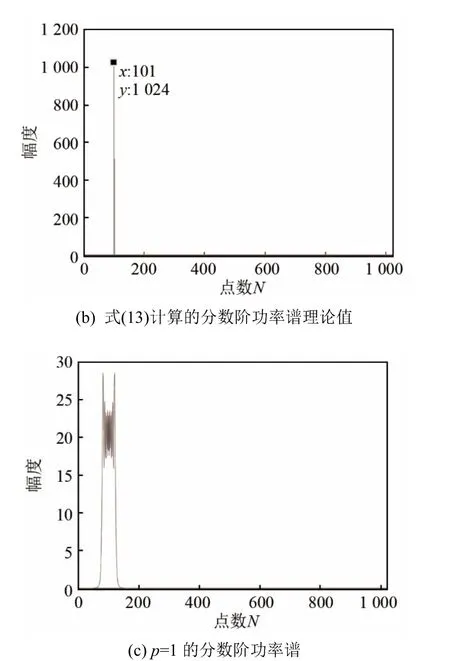
图1 LFM信号的分数阶功率谱Fig.1 Fractional power spectrum of complex LFM signal

2.2.2 HFM信号分数阶功率谱

HFM信号的FRFT解析式求解困难，这里通过仿真验证FRFT对小曲率HFM信号的聚集性。HFM 信号的双曲系数 K=-2 000，t0=7.5 s，幅度A=1，采样频率fs=1 024 Hz，点数 N=1 024。图2(a)、2(b)分别为阶数p=1.02和p=1的分数阶功率谱，对比两图可知，FRFT对小曲率HFM信号也有能量聚集性。

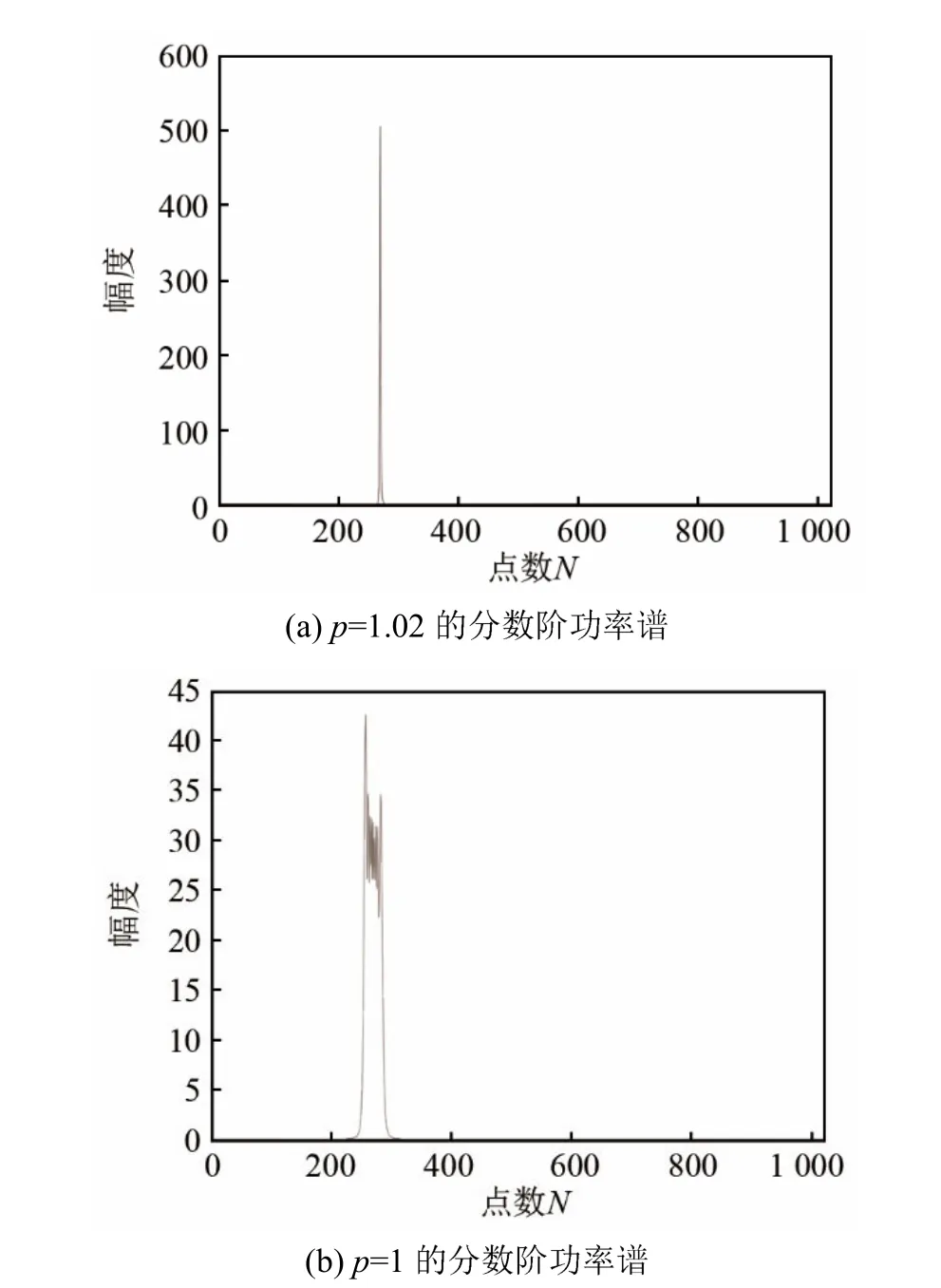
图2 HFM信号的分数阶功率谱Fig.2 Fractional power spectrum of complex HFM signal

2.2.3 FRFT处理增益分析

接收脉冲信号一般会被噪声污染。由于 HFM信号增益分析较为困难，且可将其看作类 LFM 信号，故仅分析LFM信号的处理增益。LFM信号经FRFT后，信号和带噪信号的分数阶功率谱二维分布为

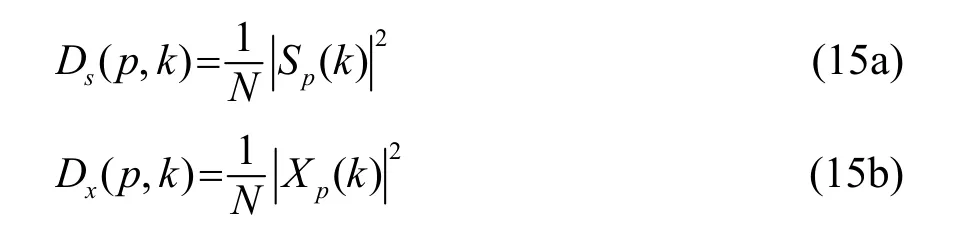
式(15a)表示LFM信号经FRFT形成的分数阶功率谱二维分布，式(15b)表示信号与均值为0、方差为的高斯白噪声形成带噪信号的分数阶功率谱二维分布。

2.3 检测流程

图3为分数阶功率谱熵检测流程，在二维平面内搜索Dx( p, k)的峰值，得到最佳变换阶数p0，再采用纽曼皮尔逊准则，对p0阶分数阶功率谱Dx( p0, k )熵检测，检测门限通过学习获取。

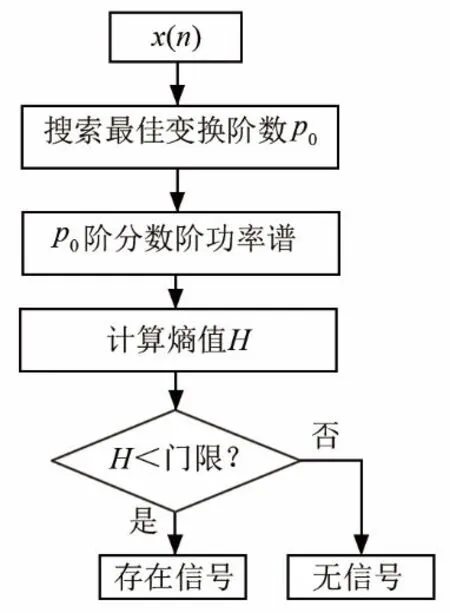
图3 分数阶功率谱熵检测流程Fig.3 Process of fractional power spectrum entropy detection

搜索最佳阶数时，为兼顾估计精度和计算量，使用一种稳定的快速算法：

(1) 在区间[0, 2]内采取大步长搜索峰值，得到阶数p1。步长设置原则为信号出现“能量聚集”(峰值谱线数值高于其他谱线 3 dB)，一般令步长s=0.1。

(2) 用e控制阶数精度，一般取e=10-4，设置循环次数i=1。

(3) 在区间[pi- s / 2, pi+ s /2]内搜索，再令搜索步长s=0.1 s，i=i+1，进行搜索得到阶数pi。

(4) 当 s≤e时，终止运算。此时最佳阶数p0=pi，否则跳转至步骤(3)。

3 数据分析

3.1 仿真数据验证

实验一：分数阶功率谱熵对未知 LFM 信号的检测性能。LFM信号中心频率f0=300 Hz，调频率k=40 Hz·s-1，幅度 A=1，采样频率fs=1 024 Hz，点数N=1 024，噪声均值为0、方差为的高斯白噪声，信噪比。图4(a)为不同信噪比分数阶功率谱熵检测器工作机接收(Receiver Operating Characteristic, ROC)曲线，检测门限由蒙特卡洛实验确定，图 4(b)为虚警概率Pfa=10-4时三种检测方法的性能对比，检测概率Pd=0.5时，要求分数阶功率谱熵检测的信噪比大约为-14 dB，优于功率谱熵检测器5.5 dB，优于能量检测器7 dB。实际上，LFM 信号带宽与功率谱熵检测器性能成反比，但分数阶功率谱熵器不受信号带宽的影响，对 LFM信号具有良好检测性能。

图4 LFM信号检测性能Fig.4 Detection performance of LFM signal

实验二：分数阶功率谱熵对未知HFM信号的检测性能。HFM 信号下限频率fL=200 Hz，上限频率fH=250 Hz，其他条件与实验一相同。图5(a)为不同信噪比分数阶功率谱熵检测器 ROC曲线，图5(b)为虚警概率Pfa=10-4检测方法的性能，检测概率Pd=0.5时，要求分数阶功率谱熵检测的信噪比大概为-12.5 dB，优于功率谱熵检测器5 dB，优于能量检测器5.5 dB。分数阶功率谱熵检测器对HFM信号的检测性能要低于 LFM 信号，但优于功率谱熵检测和能量检测。

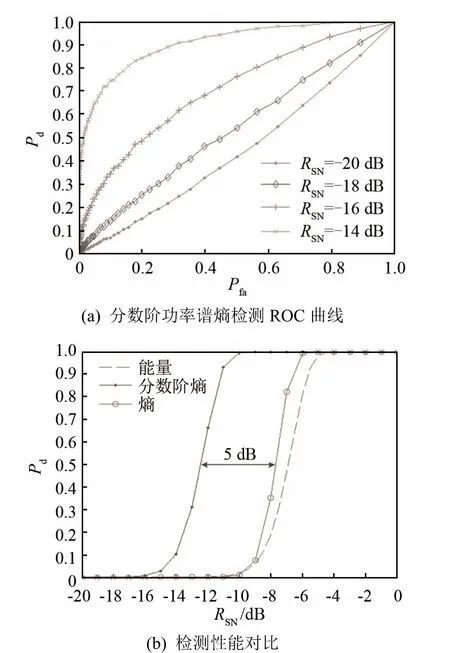
图5 HFM信号检测性能Fig.5 Detection performance of HFM signal

3.2 海试数据检验

某地海试时，声源船发射CW和LFM脉冲，选取60 s试验数据进行分析。CW信号：中心频率6.5 kHz，脉宽64 ms，重复周期9.5 s；LFM信号：中心频率6.5 kHz，带宽300 Hz，脉宽128 ms，重复周期9.5 s。

图6(a)是CW脉冲信号波形，共有6个脉冲，图 6(b)是用功率谱熵和分数阶功率谱熵处理的结果，处理时宽为128 ms，两种检测算法处理结果基本一致，都出现了6个谷值，说明对于CW脉冲信号，分数阶功率谱熵算法性能不会下降。

图6 CW脉冲信号处理结果Fig.6 Processing results of CW pulse signal

图7(a)是LFM脉冲信号波形，共有7个脉冲，图 7(b)是用功率谱熵和分数阶功率谱熵处理的结果，处理时宽为128 ms，学习门限γ= 5 .799，两种算法都检测出了7个脉冲信号。但可以看出分数阶功率谱熵值更小，说明对于LFM脉冲信号，分数阶功率谱熵检测器要优于前者。

图7 LFM脉冲信号处理结果Fig.7 Processing results of LFM pulse signal

为了验证低信噪比条件下分数阶功率谱熵的实际检测性能，截取一段无 LFM 脉冲信号的海试背景噪声数据乘以倍数来控制噪声的功率，控制信噪比，叠加到信号中。估计信号平均功率Ps，信噪比RSN= 10lg(Ps/)。图 8是仿真数据和海试数据检测概率的对比，虚警概率Pfa=10-4，两者基本吻合。检测概率Pd=0.5时，海试结果信噪比为-10 dB，验证了分数阶功率谱熵检测器在低信噪比下的工程可行性。

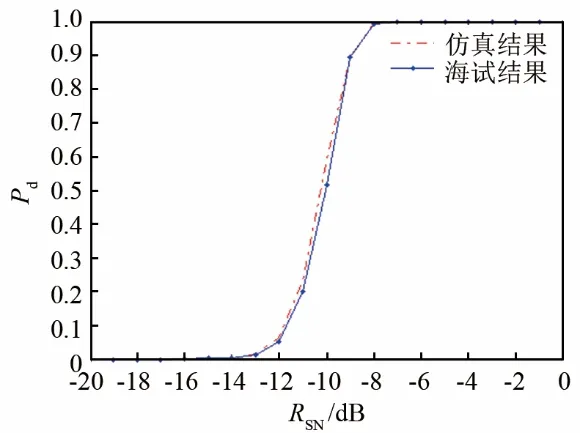
图8 海试数据和仿真数据检测性能对比Fig.8 Detection performance comparison between sea trial data and simulation data

4 结 论

针对低信噪比条件下未知水声脉冲信号的检测问题，提出了一种基于FRFT的分数阶功率谱熵检测方法。对于CW信号，该方法和功率谱熵检测算法的处理结果基本无差别，证实分数阶功率谱熵算法对CW信号检测同样适用，其性能不受算法复杂度的影响；对于LFM信号和小曲率HFM信号，该方法处理效果更优。由此，建立了分数阶功率谱熵的统一算法，实现了在无先验信息条件下水声脉冲信号的统一自动检测。

本文从理论和仿真验证了 FRFT对 LFM 和HFM信号的能量聚集作用，优化了FRFT阶数搜索方法。实验结果表明：对于 LFM 信号，分数阶功率谱熵检测器在Pfa=10-4，Pd=0.5时，检测信噪比为-14 dB，性能优于功率谱熵5.5 dB。因为小曲率HFM信号可看作类LFM信号，故当HFM信号瞬时频率缓慢变化时，性能较后者也提高了5 dB。对海上试验数据进行处理，对于 LFM 信号，在虚警概率为10-4、检测概率为0.5时，要求检测信噪比RSN=-10 dB，验证了检测器在低信噪比下的实际检测能力。