误差非线性函数的变步长FxLMS算法研究

李晓龙，卢炽华，魏晓旭，刘志恩，陈 弯

(1. 现代汽车零部件技术湖北省重点实验室，湖北武汉430070；2. 汽车零部件技术湖北省协同创新中心，湖北武汉430070)

0 引 言

自适应滤波算法是主动噪声控制研究的重点，基于最速下降算法的最小均方(Least Mean Square,LMS)算法由Windrows等1]于1959年提出，因其易于实现、稳定性好而受到广泛应用。但 LMS算法的收敛速度与稳态误差之间存在矛盾，即当步长因子取值较大时可加快收敛速度，但稳态误差变大；反之步长因子取值较小时，收敛速度变慢，无法满足算法实时性需求。为解决这一问题，覃景繁等[2]提出了一种步长因子与误差成Sigmoid函数关系的变步长LMS算法，并给出了步长因子的调整原则：算法收敛初期需具有较大的步长因子以保证收敛速度，在接近收敛时则需较小的步长因子以保证稳态误差。基于该调整原则，部分文献提出了其他的基于误差非线性函数的步长因子调整模型。邓江波等[3]提出了基于箕舌线的变步长LMS算法，无需指数运算从而降低了算法的复杂度。詹国强等[4]提出了一种新的变步长 LMS算法，该算法步长因子与误差的关系为抽样函数，相比于S型函数在更大程度上解决了收敛速度与稳态误差的矛盾。文献[5-7]中使用双曲正切函数作为步长因子的调整函数，结果表明收敛速度和稳态误差均优于标准LMS算法。朱斌等[8]使用反正切函数控制步长因子，管四海等[9]对其进行改进，全面提升了算法的性能。卢炳乾[10]、王蕾等[11]使用正弦函数来调整步长因子，在降低计算时间的同时有效控制了稳态误差的失调量。罗海富等[12]为进一步提升收敛精度使用双曲正弦函数调整步长因子。茹国宝等[13]将刘剑锋等[14]提出的基于洛伦兹函数的变步长 LMS算法进行了推广，得到了基于对数函数的变步长 LMS算法，不仅大大降低了计算量，收敛速度和稳态误差也表现出更好的性能。

将 LMS算法用于主动噪声控制时，由于未考虑次级通路的影响，权系数的迭代将基于参考信号而非滤波参考信号，导致降噪效果变差。Burgess等[15]提出的滤波-x 最小均方(Filtered-x Least Mean Square, FxLMS)算法考虑了次级通路的影响，成为主动噪声控制最常用算法。与变步长 LMS算法相似，为改善 FxLMS算法的收敛速度与稳态误差，部分文献将上述非线性函数或其改进形式应用于FxLMS算法。Gomathi等[16]引入反正切函数控制FxLMS算法的步长，获得了更快的收敛速度和更高的消声量。张帅等[17]对其进行了改进，将步长因子对参考信号的功率做了归一化处理，提高了控制非稳态噪声时的稳定性。张帅等[18]还将文献[11]中的正弦函数推广到更一般的情况，并应用于变步长主动噪声均衡控制，进一步降低了车内噪声响度，而其他非线性函数在变步长 FxLMS算法中的应用还不多见。

本文首先归纳了基于误差非线性函数的步长因子调整模型，按运算类型将其分为四类。分析了调整模型的参数项对步长因子的影响，为应用算法时参数的选取提供参考。最后以三种常见的噪声作为输入参考信号，以收敛速度和稳态误差为评价指标，通过仿真试验对比了算法的性能。

1 变步长FxLMS算法

变步长FxLMS基本原理与固定步长FxLMS一致，实际上是考虑了次级通路影响的 LMS算法，其原理如图1所示。图1中：x( n)是参考传感器在噪声源采集的参考信号，表示初级声源到误差麦克风的初级通路，d(n)表示由噪声源产生的初级噪声，W(z)表示自适应控制滤波器，配合FxLMS算法控制滤波器的输出u(n)。Hs(z)表示 u(n)到误差麦克风的次级通路，( z)是 Hs(z)的估计，通常用长度一定的有限脉冲响应(FIR)滤波器来建模，理想情况下。y(n)为到达误差麦克风处的抵消噪声，e(n)是误差麦克风采集到的误差信号， xf( n)为滤波参考信号。

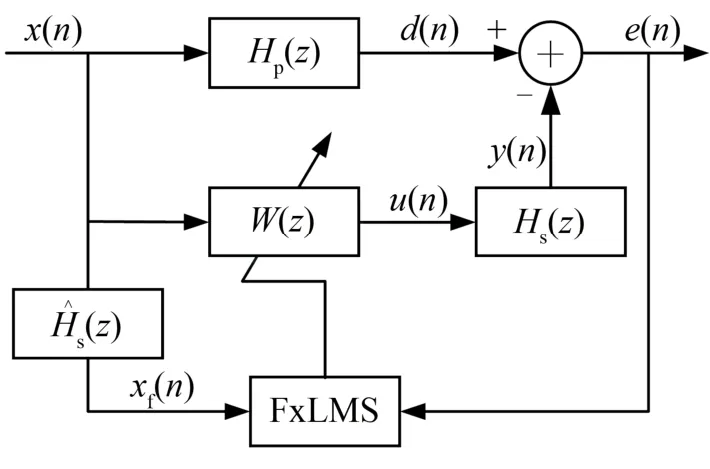
图1 FxLMS算法原理图Fig.1 Principle diagram of FxLMS algorithm

变步长FxLMS算法计算过程如下：

(1) 通过离线次级通路识别技术，得到次级通路脉冲响应的估计式中：L是FIR滤波器的长度。

(2) 当 u(n)经次级通路传播到误差麦克风处时，可表示为

(4) 测量误差信号 e(n)。控制滤波器输出信号u(n)经次级通路后得到 y(n)，它与初级噪声 d(n) 干涉相消，残余噪声 e(n) 被误差麦克风采集，参与权系数的迭代更新。

(5) 更新控制滤波器权系数。权系数更新迭代公式为

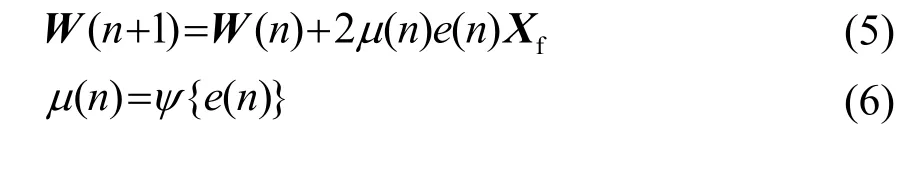
式中：μ(n)为步长因子，ψ{e(n)}表示以e(n)为自变量的非线性函数。

2 基于非线性函数的变步长模型

通过已有研究，目前一般采用的 ψ{e(n)} 基本形式共有9种，控制参数最多不超过3个。通过观察可以发现，Sigmoid函数与双曲正切函数具有类似的形式，通过简单的通分运算并将系数参数化即可得到广义的Sigmoid函数模型，其步长因子表达式为

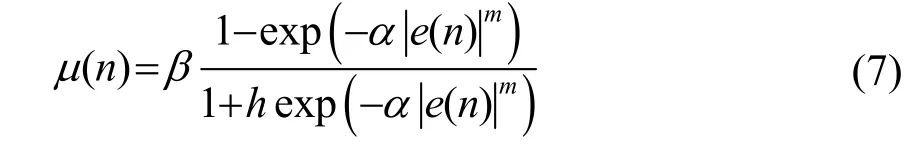
当 h=1时，式(7)变为 Sigmoid函数；当 m=1时，式(7)变为双曲正切函数。通过观察还可以发现，对数函数模型实际上是洛伦兹函模型更一般的情况，其表达式为 μ ( n) = βlg(α| e ( n )|m+1)，当α = 1 /δ2且m=2时，对数函数变为洛伦兹函数。对模型数量进行删减并按运算类别进行分类，最终非线性函数模型被缩减为7个，可分为4类，即指数运算类、三角函数运算类、对数运算类和基本运算类，如表1所示。

表1 基于不同误差非线性函数ψ{e(n)}的变步长模型Table 1 Variable step models based on different error nonlinear functions ψ{e(n)}

3 变步长参数影响特性分析

3.1 参数m的影响

参数m表示e(n)次幂运算的次数，先单独讨论m的影响。包含参数m的模型共有4个，分别是广义Sigmoid函数、双曲正弦函数、反正切函数和对数函数。固定其他参数，令m=1, 2, 3, 4，分别得到m对误差-步长因子(e-μ曲线)的影响，结果如图2所示。

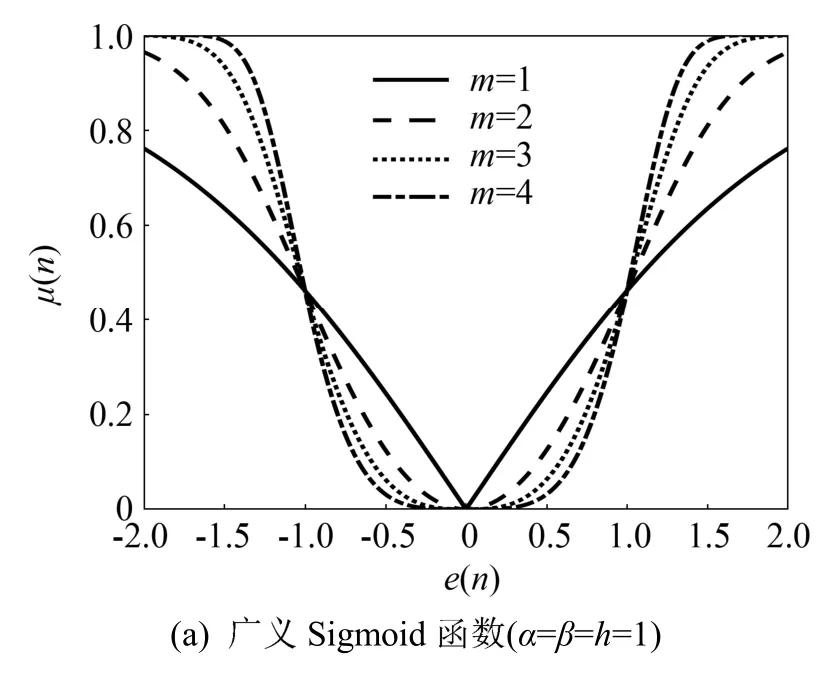
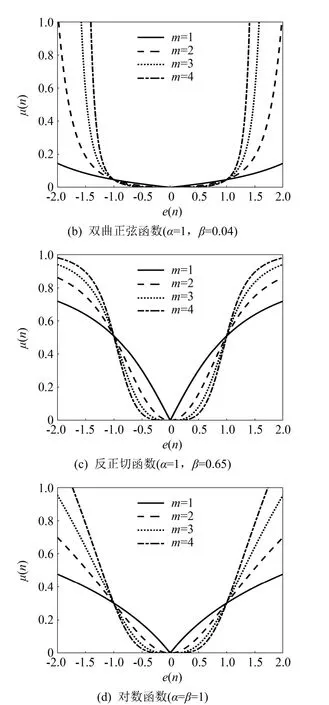
图2 参数m对不同模型e-μ曲线的影响Fig.2 The influence of parameter m on e-μ curve of different models

由图2可知，理论上m取值越大，算法性能会越好。在算法计算初期将具有更大的μ( n)，保证算法快速往最优权值方向搜索，在算法接近收敛时μ( n)变化更缓慢，可保证较好的稳态误差。但 m取值过大会使e-μ曲线底部更为平坦，这将导致在误差较大时μ( n)就减小到较小的值，导致算法收敛速度变慢，同时增大m会增加算法的计算量，一般m取1或2[6,8]，本节的分析中取m=2。

3.2 指数运算类

3.2.1 广义Sigmoid函数模型

α、β、h对广义Sigmoid函数模型e-μ曲线的影响如图3所示。由图3可知，参数β直接决定了μ( n )的最大值，在保证算法收敛的情况下，可尽量取较大值。α和h则可以控制曲线底部的平坦程度，若需要在误差较大时采用较大的μ(n)，则增大α或减小h，反之则减小α或增大h。总之，通过合理设置α和h的值可使算法性能达到最佳。

图3 参数β、α、h对广义Sigmoid函数模型e-μ曲线的影响Fig.3 The influence of parameter β, α, h on e-μ curve of generalized Sigmoid function model

3.2.2 双曲正弦函数

β、α对双曲正弦函数模型e-μ曲线的影响如图4所示。β控制曲线的缩放比例，而α则影响曲线的整体形态，增加β、α可提高收敛速度，但稳态误差会变差。此外，α不可取值过大，否则会使得μ(n)随着算法的收敛呈直线下降，最终可能出现这种情况：μ(n)虽然小于保证算法收敛的最大步长因子μmax，但由于μ(n)下降得过快，会导致μ(n)较小，而此时μ(n)本可以取更大的值以实现更快的收敛速度。

图4 参数β、α对双曲正弦函数模型e-μ曲线的影响Fig.4 The influence of parameter β, α on e-μ curve of hyperbolic sine function model

3.3 三角函数运算类

3.3.1 抽样函数

β、α对抽样函数模型e-μ曲线的影响如图 5所示。与双曲正弦函数类似，若对收敛速度有较高要求，则选取较大的β和α值；若对稳态误差有较高要求，则选取较小的β和α值。需要注意，如图5(b)所示，α取值过大会导致e-μ曲线中出现旁瓣，这意味着随着误差e(n)的减小，μ(n)反而可能增大，导致算法不稳定。

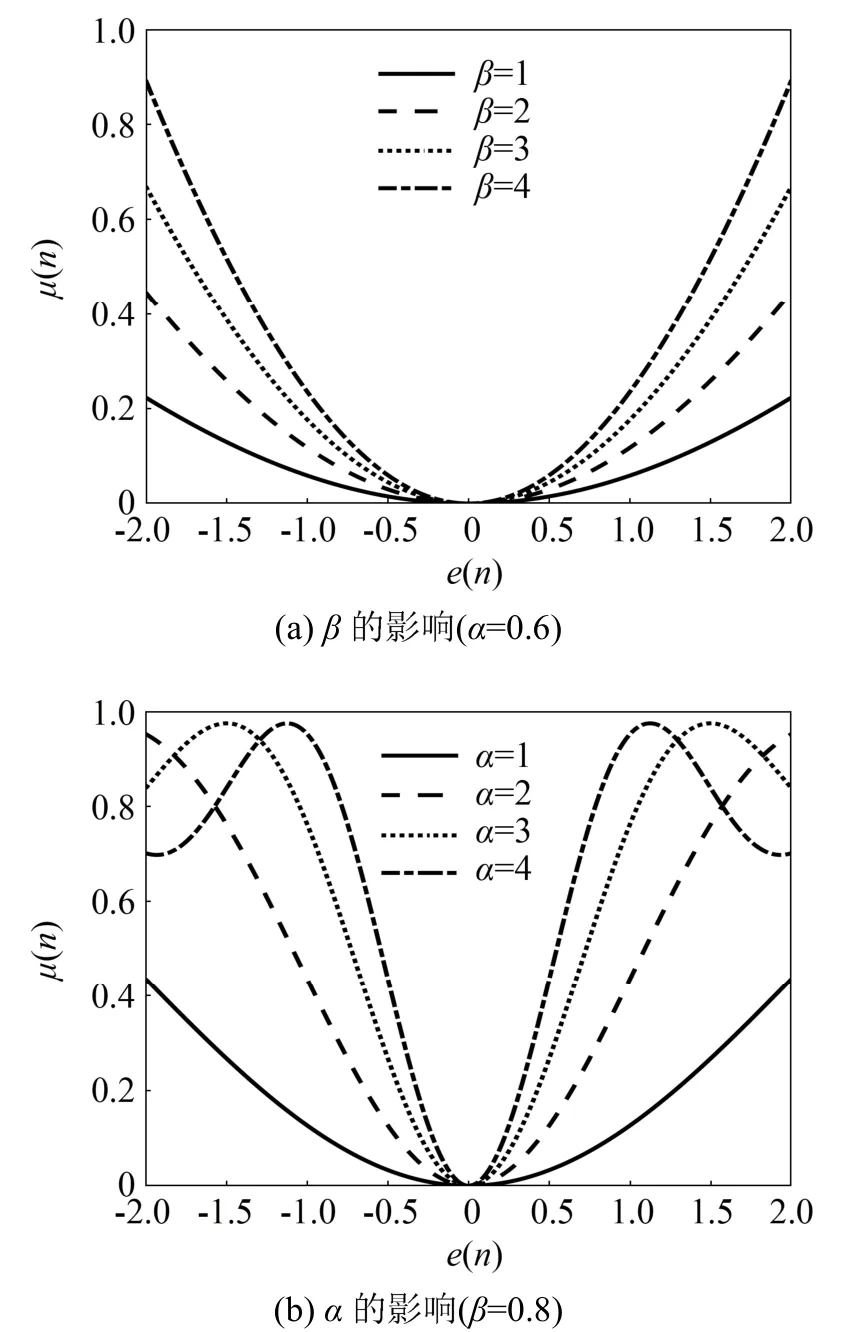
图5 参数β、α对抽样函数模型e-μ曲线的影响Fig.5 The influence of parameter β, α on e-μ curve of sampling function model

3.3.2 反正切函数

β、α对反正切函数模型e-μ曲线的影响如图6所示。由图6可知，β决定了μ(n)的取值范围，可用于限制μ(n)的最大值，其取值应确保μ(n)值处在算法可收敛的范围内。α则主要影响曲线底部的形态，其取值越大曲线底部越尖锐，也就是说e(n)接近0时，μ(n)变化越大，算法在收敛时维持稳态误差精度的能力越差。

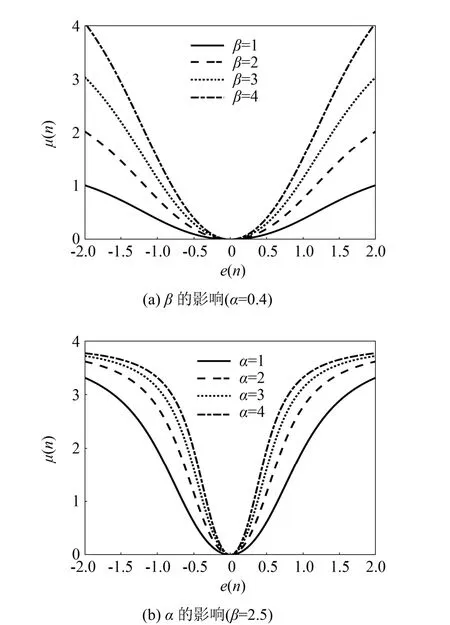
图6 参数β、α对反正切函数模型e-μ曲线的影响Fig.6 The influence of parameter β, α on the curve of arc tangent function model

3.3.3 正弦函数

β、α对正弦函数模型e-μ曲线的影响如图7所示。β决定了μ(n)的最大值，而α更大程度地影响e-μ曲线的底部形状。若要获得较快的收敛速度和跟踪速度，则应增加β和α；反之，若要获得较小的稳态误差，则应减小β和α；若β和α的取值过小，变步长函数将退化为固定步长函数。此外，正弦函数与抽样函数同样存在α取值过大使e-μ曲线出现旁瓣的问题。

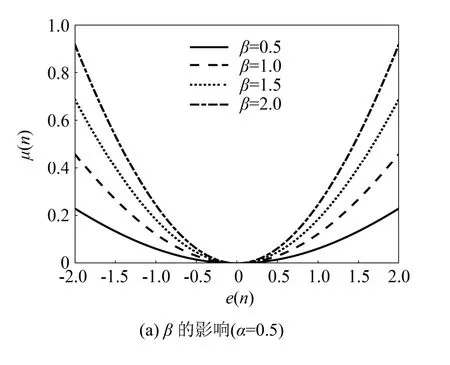
图7 参数β、α对正弦函数模型e-μ曲线的影响Fig.7 The influence of parameter β, α on e-μ curve of sinusoidal function model

3.4 对数函数

β、α对对数函数模型 e-μ曲线的影响如图 8所示。其中，β控制曲线的开口宽度，α控制曲线的底部形态，α取值越大，曲线底部越尖锐，这表示在算法接近收敛时，μ( n )波动较大，使控制滤波器权系数错过最佳收敛值，导致稳态误差变大。

图8 参数β、α对对数函数模型e-μ曲线的影响Fig.8 The influence of parameter β, α on e-μ curve of logarithmic function model

3.5 箕舌线函数

β、α对箕舌线函数模型e-μ曲线的影响如图9所示。对比图9和图6可以发现，两者具有相似的形态。因此，在主动控制的过程，对于同一噪声源两者会表现出相似的性能，但箕舌线函数只包含基本的加减乘除运算而无需计算反三角函数，若要选择两者之一，可优先选择计算量小的箕舌线函数。

图9 参数β、α对箕舌线函数模型e-μ曲线的影响Fig.9 The influence of parameter β, α on e-μ curve of tongue-like function model

3.6 总 结

通过以上分析可知，当 m确定时，除广义Sigmoid函数模型有3个可调参数外，其他函数均只有2个可调参数。其中β的主要作用是控制e-μ曲线整体的形态，β越大则μ( n )整体越大；α则主要控制曲线底部的形态，α越大不仅曲线底部更窄，μ( n )也不同程度地增大。因此在调试算法参数时，存在增大其中一个必然要减小另一个的矛盾。若为保证收敛速度而选择较大的β，则α应取较小的值，e-μ曲线底部会趋于平缓，可能会导致误差较大时收敛速度变慢；若选取较小的 β，则为保证收敛速度需相应地增加α，这会使e-μ曲线底部趋于尖锐，导致算法稳态误差变大。通过引入额外的参数可解决此矛盾，例如广义Sigmoid函数中增加了参数h来调整函数整体的形态，从而使算法性能更好。但参数越多，调整参数所需的试验时间也越多，因此只有在需要实现特殊的性能时才考虑具有3个以上参数的算法[19]。

4 算法性能对比

为对比不同噪声环境下算法的性能，选取三种常见噪声源作为参考输入信号[20]。假设次级通路Hs(z)与它的估计( z)相等。初级通路 Hp(z)和次级通路Hs(z)均用FIR滤波器建模，滤波器长度均为 128，两者的频率响应参考文献[21]，频率响应曲线如图10所示。设置控制滤波器长度N= 1 28。以平均降噪量[22](Average Noise Reduction, ANR)作为评价指标，其定义式为

图10 初级通路与次级通路频率响应曲线Fig.10 Frequency response curves of primary path and secondary path

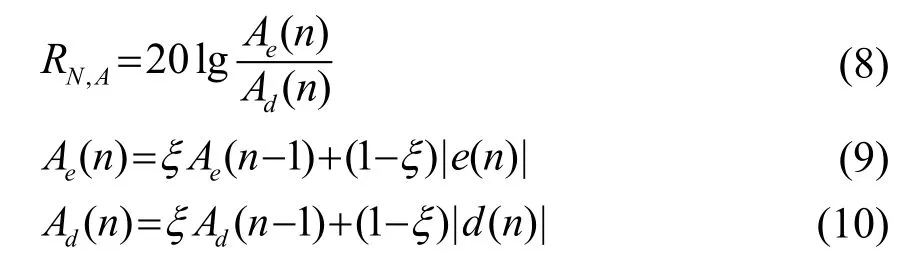
4.1 高斯白噪声输入

本例选取均值为 0、方差为 0.1的高斯白噪声作为参考信号x( n)，仿真参数如表2所示。

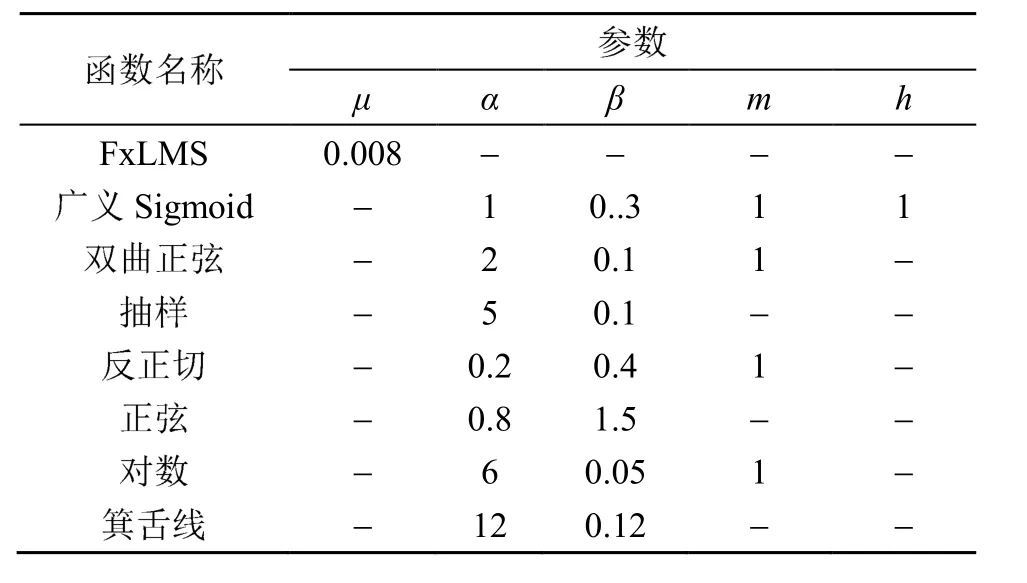
表2 参考信号为高斯白噪声时的仿真参数Table 2 Simulation parameters for Gaussian white noise input

图 11对比了各算法仿真结果。参考输入为高斯白噪声时，各算法性能均优于固定步长 FxLMS算法，其中对数函数算法具有最低的稳态误差，但收敛速度较快；双曲正弦函数算法具有最快的收敛速度，但稳态误差较大；箕舌线函数算法综合性能最好，其收敛速度和稳态误差均表现较好。

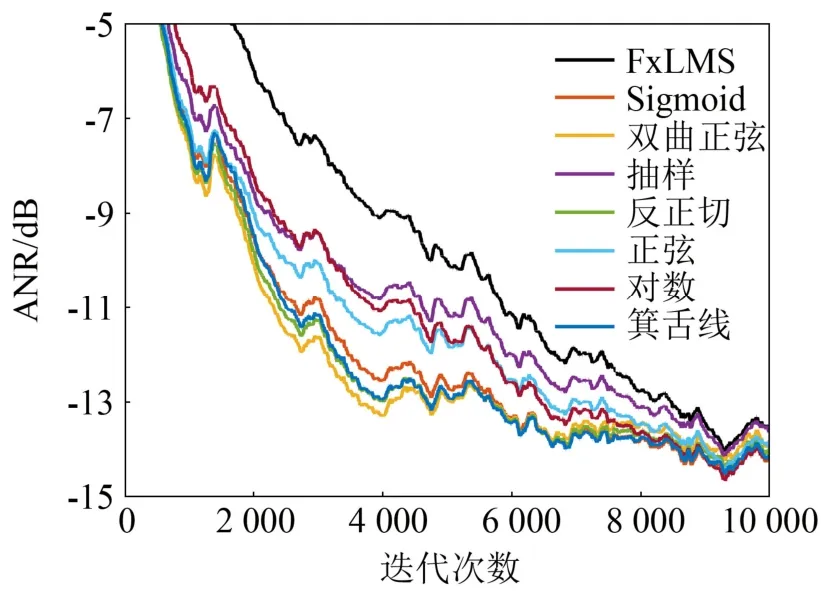
图11 参考信号为高斯白噪声时的ANR曲线Fig.11 ANR curves for Gaussian white noise input

4.2 正弦波输入

本例选取频率为 500 Hz的正弦波作为参考信号x( n)，加入信噪比为40 dB的高斯白噪声，采样率设置为5 000 Hz，其表达式为

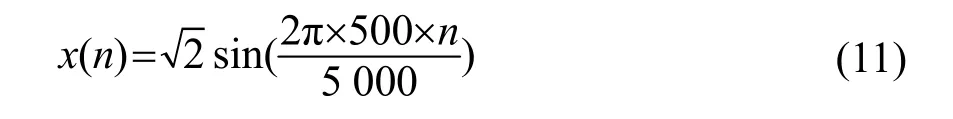
仿真参数如表3所示，图12给出了各算法仿真结果。参考输入为正弦波时，各算法性能同样优于固定步长FxLMS算法，其中广义Sigmoid函数与对数函数算法性能较好，它们具有相对较快的收敛速度和较低的稳态误差；正弦函数和抽样函数算法在迭代过程中有一段收敛速度慢于标准算法，这是因为在误差较大时步长因子就降低至较小值，导致收敛速度变慢。

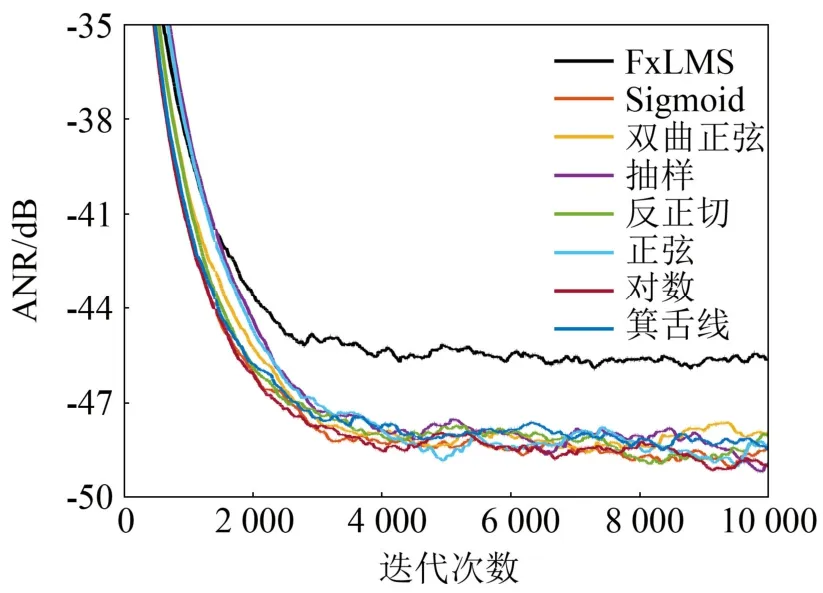
图12 参考信号为正弦波时的ANR曲线Fig.12 ANR curves for sinusoidal wave input

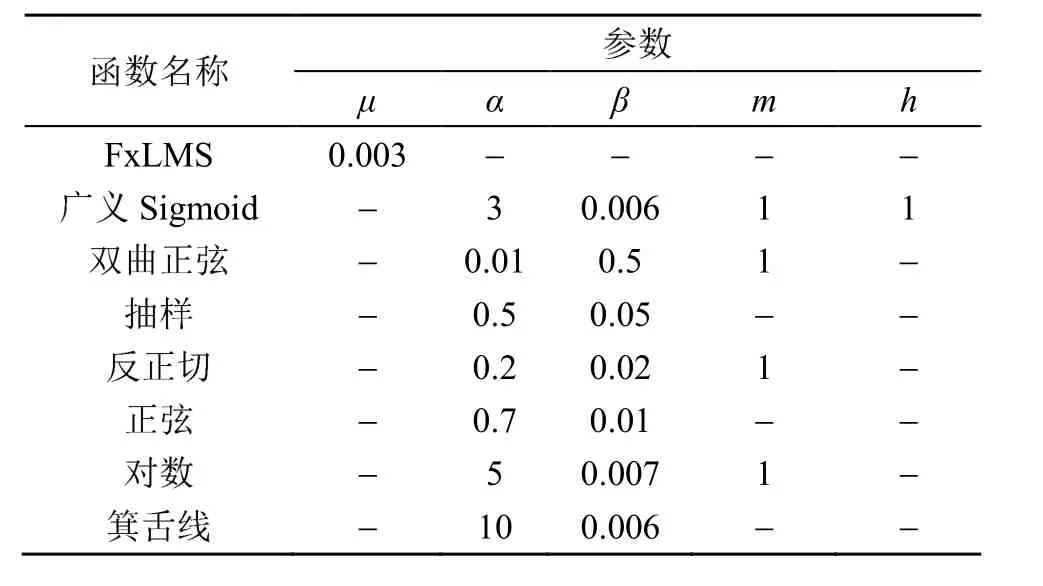
表3 参考信号为正弦波时的仿真参数Table 3 Simulation parameters for sinusoidal wave input

4.3 冲击噪声输入

本例选取冲击噪声作为参考信号x(n)。冲击噪声用对称α稳定(SαS)噪声模型(使用McCullonch[23]开发的Matlab函数stblrnd，α=1.8)建模。仿真参数如表4所示。

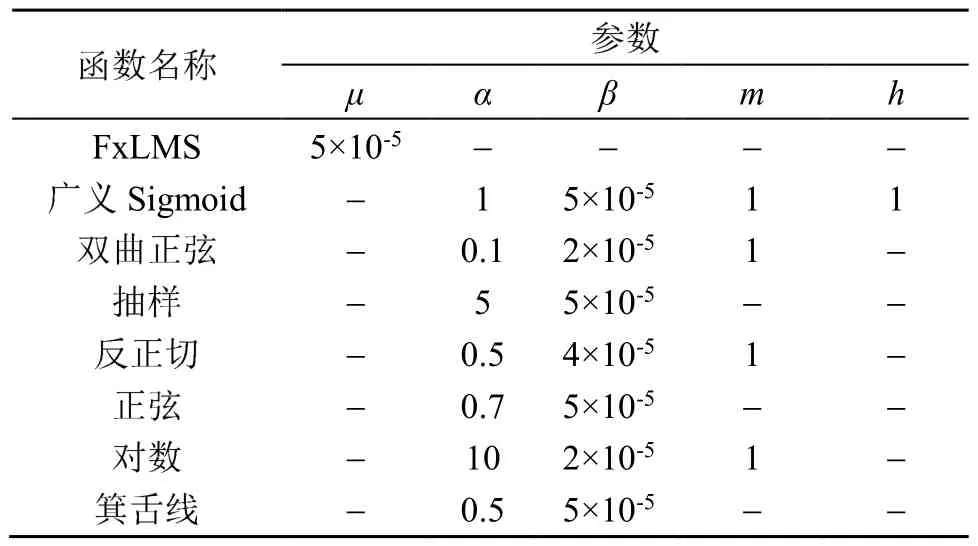
表4 参考信号为冲击噪声时的仿真参数Table 4 Simulation parameters for impulsive noise input

图 13给出了各算法的仿真结果。与参考输入为高斯白噪声和正弦波时不同，各算法均未能表现出比固定步长更好的性能，这是因为冲击噪声幅值较大，导致e(n)较大，为保证算法收敛β取值很小，此时α取值对e-μ曲线影响不大，曲线底部变得平坦，变步长算法退化为固定步长算法；其中双曲正弦函数算法β取值最小，故收敛速度最慢。

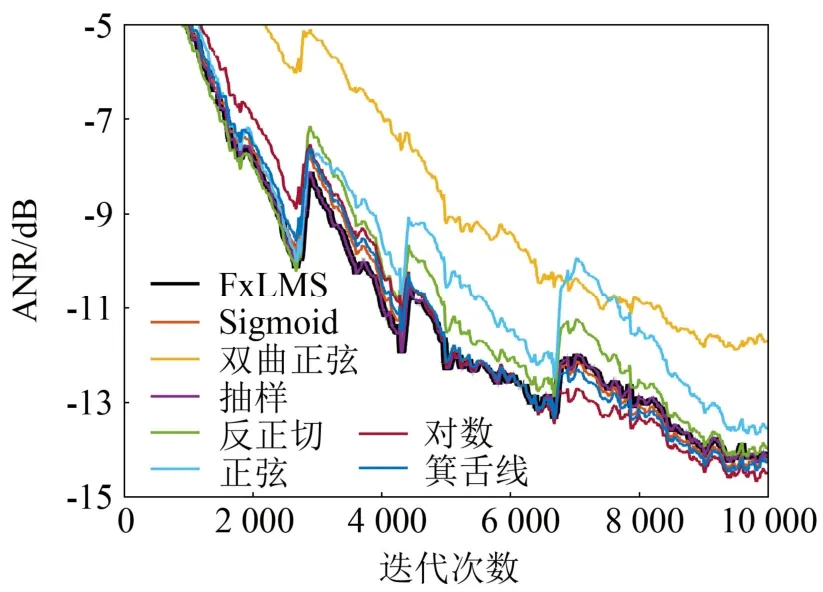
图13 参考信号为冲击噪声时的ANR曲线Fig.13 ANR curves for impulsive noise input

5 实车主动噪声控制试验

为验证变步长模型的实用性，将变步长FxLMS算法应用于某车型的单通道发动机主动噪声控制试验中。采用霍尔传感器作为参考传感器，获得单位时间的点火脉冲数，由此计算出当前发动机的转速，进而获得要抵消的发动机的噪声频率。驾驶员座椅头枕右侧布置两个麦克风，一个作为主动噪声控制系统的误差麦克风，另一个则用于采集开启主动噪声控制系统前后头枕右侧噪声的变化。次级扬声器固定于中央台扶手。参考传感器、麦克风以及次级声源布置位置分别如图 14(a)、14(b)所示。

图14 参考传感器、误差麦克风和次级声源布置位置图Fig.14 The layout for reference sensor, error microphone and secondary source

本次试验使用对周期噪声控制效果较好的广义Sigmoid函数调整迭代步长。试验工况分别为定速(3 500 r·min-1)工况和三挡全油门(Wide Open Throttle, WOT)即3WOT加速工况。采用LMS Test.Lab测试系统采集开启主动噪声控制系统前后，驾驶员头枕右侧的声压变化，由此计算 ANR曲线，用于对比不同算法的性能。

定速工况测试结果如图 15所示。相较于传统FxLMS算法，变步长FxLMS算法可以获得更快的收敛速度和较低的稳态误差。3WOT工况测试结果如图16所示。与定速工况结果不同，3WOT工况时，变步长算法并没有表现出明显的优越性，这是因为3WOT工况发动机噪声随转速变化速度很快，控制滤波器权系数还未收敛至最佳值，就进入下一个转速点的迭代。

图15 定速工况的ANR曲线Fig.15 ANR curve for constant speed condition

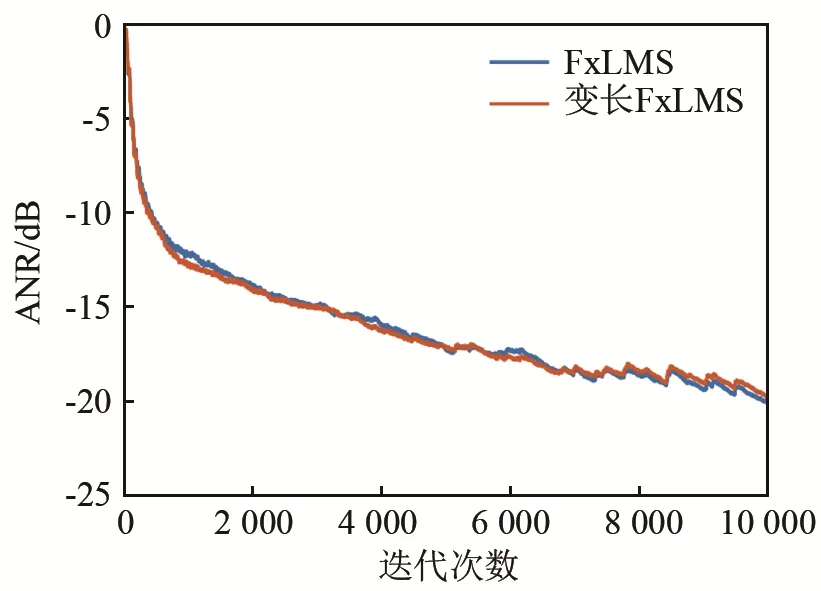
图16 3WOT工况的ANR曲线Fig.16 ANR curve for the 3WOT gear condition

6 结 论

本文总结了现有基于误差非线性函数模型的变步长LMS算法，分析了各模型中参数项对e-μ曲线的影响，并将其应用于 FxLMS算法，使用三种常用噪声信号作为参考输入，对比了各算法的收敛速度和稳态误差，为不同噪声源的算法选取提供了参考。结果表明：对于高斯白噪声，基于箕舌线函数的变步长算法综合性能最优；对于正弦波，则是广义Sigmoid函数和对数函数变步长算法性能较好；对于冲击噪声，基于误差非线性函数的变步长算法并不能表现出更好的性能，也就是说，此类变步长算法不适用于冲击噪声的主动控制。最后，将基于广义Sigmoid函数的变步长FxLMS算法应用于某车型的发动机主动噪声控制，结果显示：对于定转速工况，变步长算法能获得更好的收敛速度和稳态误差；对于3WOT工况，变步长算法性能则未能表现出明显的优势。