声呐渗流测量数据降噪的分类模型研究

杜家佳，卜 凡，杜国平,，王永利，宋晓峰，杜建平

(1. 南京帝坝工程科技有限公司，江苏南京210094；2. 南京理工大学，江苏南京210063；3. 广西帝坝科技公司，广西南宁530021)

0 引 言

土木工程建设具有工程规模大、环境条件复杂、施工风险高等特点，在工程事故中因渗漏引起的故事高达62%，造成了巨大的经济损失和广泛的社会影响。而究其原由是没有一种能够在天然流场下定量定位测量出地下隐蔽工程渗漏缺陷的技术方法[1]。声呐渗流探测技术作为原创性声呐渗流测量技术，先后在国内外的百余项各类大中型工程上应用与推广，得到业界的普遍认可和好评。声呐渗流探测技术利用声波在水中的优异传播特性而实现对水流速度场的测量。如果被测水体存在渗流，则必然在测点产生渗流场，声呐探测器阵列能够精细地测量出声波在流体中能量传递的大小，依据声呐传感器阵列测量数据的时空分布，即可生成土木工程需要的原位渗流场的渗透流速、渗流方向、渗流量、渗透系数等各种水文地质参数[2]，从而对渗流情况进行判断。然而由于噪声干扰的存在，会影响对渗流属性的判断。因此有必要对渗流波形与噪声波形进行建模、计算与分类，以计算机的手段与方法快速、准确地识别、分离干扰噪声以保证对真实渗流的判断与甄别。

目前对声呐波形进行分类的研究并不多，效果较好的包括通过传统波形分析[3-4]以及通过并行网络[5]、分层网络[6]、通用回归网络(General Regression Neural Network, GRNN)[7]等神经网络模型的声呐分类方法。传统波形分析方法难以在较短的时间内完成对渗流类型的分类，而现有经过属性标注的真实渗流声呐波形数据量不足以支撑神经网络的学习，且神经网络的可解释性较差，较难探究声呐的分类过程。

梯度提升树(Gradient Boosting Decision Tree,GBDT)[8]是一种基于boosting[9]思想的、泛化能力较强的模型，通过对回归树进行梯度增强，可以产生有竞争力的、高度健壮的、可解释的回归和分类过程。实验表明，梯度提升树模型能够较好地对渗流的声呐数据进行分类。

实现声呐渗流检测结果分类要求模型有较强的鲁棒性。考虑到实际使用时数据的时效性，该模型需要在较短的训练过程中获得相对较高的准确率，以便对不同的地区进行针对性判断。本文出于对属性标注的渗流声呐数据特征复杂性、声呐数据类型多样性以及噪声数据干扰普遍性的考虑，提出了基于声呐声波与梯度提升树的声呐渗流检测结果分类模型。利用梯度提升树高灵活性、高鲁棒性、高准确率的特性，挖掘水库渗流与井孔渗流的分类依据并将其与噪声声波区分开，最后利用该模型对日常渗流声呐数据进行自动区分。

1 模型建立

声呐渗流检测结果分类模型的任务是对未标注的声呐数据集进行自动分类，为了实现该目标需要训练一个自动分类模型，模型的整体结构如图 1所示。

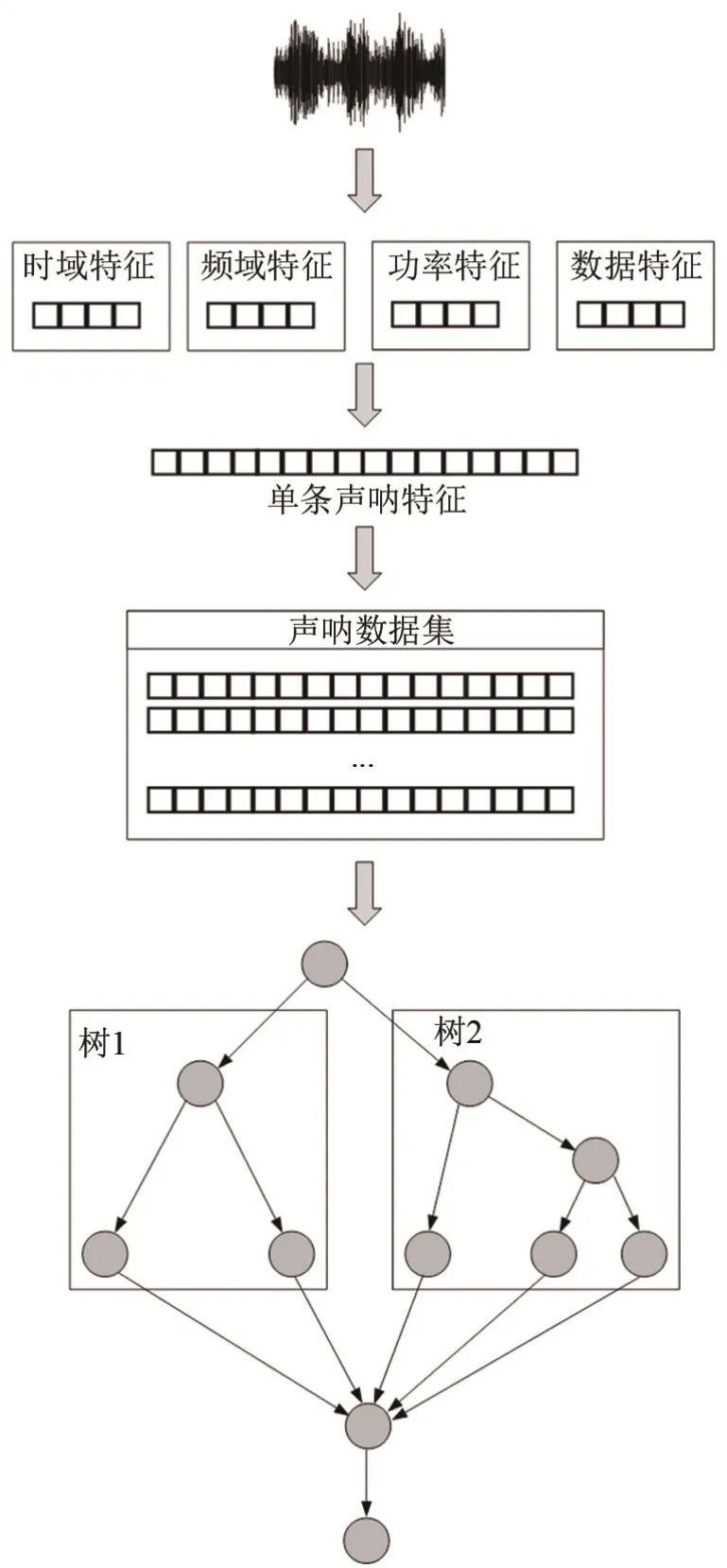
图1 声呐渗流检测结果分类模型整体结构Fig.1 The overall configuration of the classification model of sonar seepage detection results

该模型可分为以下步骤：(1) 建立样本集；(2)训练分类模型。

2 建立样本集

2.1 声呐数据信息

用于训练的渗流的声呐数据由 2013—2019年间包括廖叶湾和鲁地拉水电站等在内不同地区工程的实测波形组成。数据均采用Brüel & Kjær声学与振动测量公司的 8104型通用水听器录制，采样精度为16 bit，采样频率为 600 Hz。通过属性标注从中标注出了三类数据共 7 848条，其中包括了2 998条噪声数据、3 656条井孔渗流数据、1 194条水库渗流数据。

2.2 声呐信号预处理

声呐信号属于时间序列信号，故利用单位根检验(Augmented Dickey-Fuller Test, ADF)对其进行平稳性分析。由单位根检验可知用于训练的声呐信号为平稳序列，说明其围绕常数上下波动且范围有限，有常数均值与常数方差。由于声呐信号采样总点数较少，故将其帧长取为1 s。

首先，需去除原始声呐信号的直流干扰。其次，从时域谱、频域谱、功率谱与数据特征四个维度共提取出 36维声呐信号特征。其中，从时域谱提取的特征有平均值、峰差、峭度、偏度、脉冲因子、裕度因子等 15维特征。频域谱通过快速傅里叶变换(FFT)算法[10]获得，从频域谱提取的特征有振幅平均值、振幅峰差、重心频率、均方频率、均方根频率等11维特征。进行功率谱变换时，设声呐信号s( t)在时间段t∈ [- T / 2,T /2]上用sT( t)表示，且sT( t)的傅里叶变换为FT(ω)= F FT[sT( t )]，则功率谱P(ω)的表达式为

从功率谱提取的特征有功率最大值、功率最小值、信噪比等5维特征。从数据特征提取的特征有数据分类、声道数、采样总点数等5维特征。图2为一个声呐信号及其转换的不同谱图。

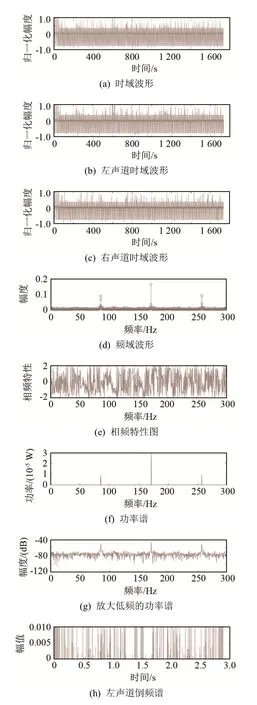
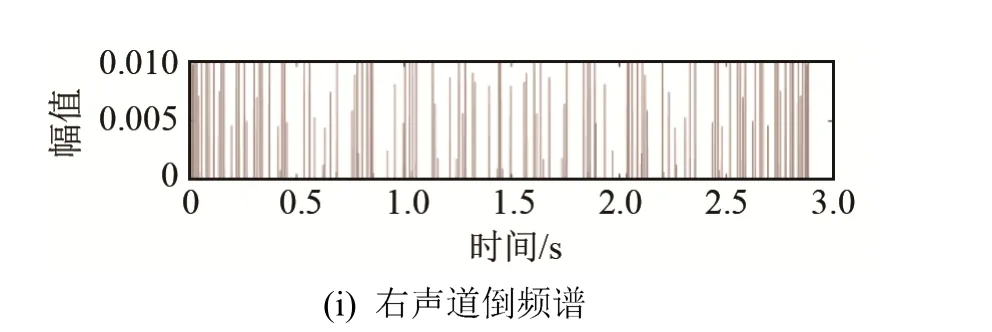
图2 一段典型的声呐信号分析图Fig.2 A typical sonar signal analysis diagram

由于不同维数据的量纲差距较大，为提高对比实验精度，对数据进行归一化处理。本文采用z-score归一化，表达式为

其中：σ为数据标准差，μ为样本均值。归一化后数据的平均值为0，方差为1。

2.3 特征选择

ReliefF算法[11]改进了Relief算法只能处理二分类特征选择的问题，使其能够处理多分类问题，而本文提出的分类模型本质上是一个多分类模型。设声呐数据集为 D，包含类别为 y，对于实例si，若它属于第k类，则先在第k类样本中寻找si的最近邻si,nh作为猜中近邻，然后在第k类之外的每个类别的样本中寻找实例si的最近邻si,l,nm，作为猜错近邻。则相关统计量对应于属性j的分量表达式为

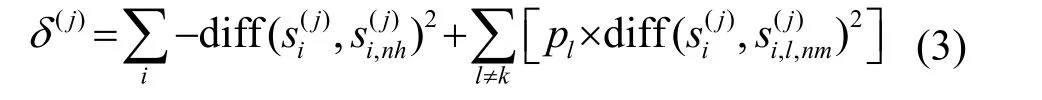
其中，pl为第l类样本在声呐数据集D中所占的比例，diff(a,b)为a与b两个特征的值的差。

3 训练分类模型

分类模型的训练模块包含预处理模块、训练模块、验证模块与输出模块四部分，模块具体内容如图3所示。

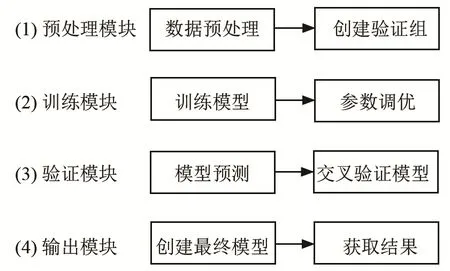
图3 分类模型训练模块Fig.3 Training modules of the classification model

决策树算法[12]具有良好的时间复杂度与模型易读性，但容易过拟合。梯度提升树基于 boosting思想对决策树算法进行了优化，其核心思想是利用损失函数的负梯度在当前模型的值作为残差的近似值，本质是对损失函数进行一阶泰勒展开，从而拟合回归树。

梯度提升树算法的计算流程如下：

(1) 输入：

4 实 验

4.1 实验环境

实验环境的操作系统为Windows 10，CPU为Intel i7-7700HQ，RAM大小为16GB。

4.2 实验结果

4.2.1 特征选择结果

通过ReliefF算法计算的贡献权重如图4所示，可以看出对区分渗流波形贡献最大的属性为功率平均值，对分类的贡献度达到了1.892。较为重要的属性包括了功率平均值、振幅平均值、振幅峰差、振幅最大值、振幅峰值阈值等。

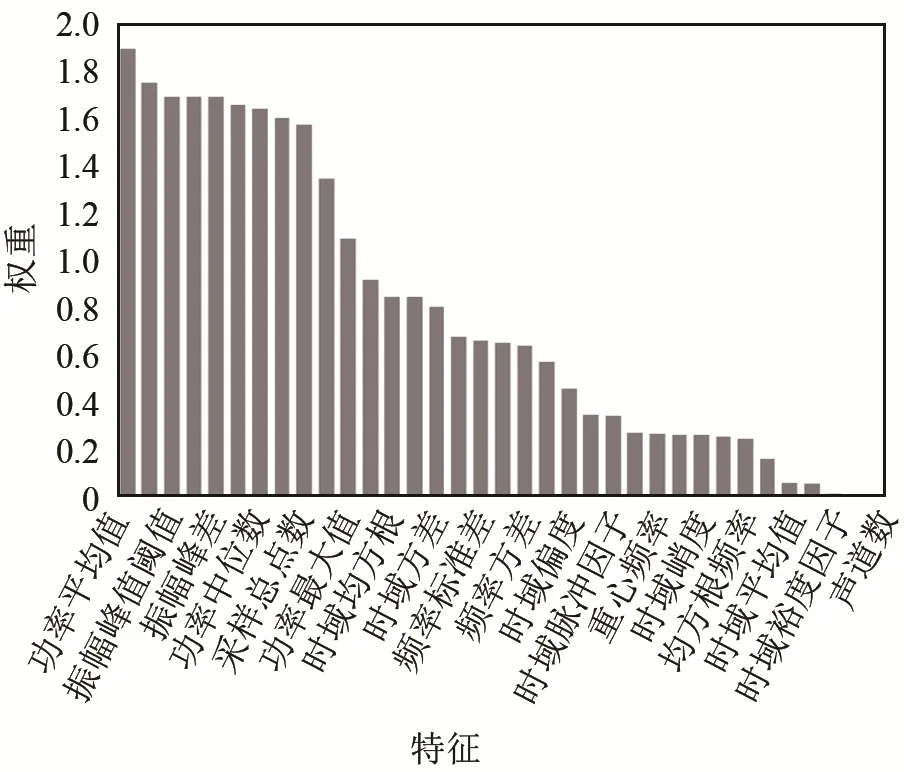
图4 ReliefF算法计算出的贡献权重Fig.4 The contribution weights calculated by ReliefF algorithm

为了选取合适的阈值并验证 ReliefF算法对结果的影响，对最大树数量为 5、最大深度为 5、学习率为 0.1的梯度提升树分别取不同阈值进行训练，训练数据集包括1 000条噪声数据、1 000条井孔渗流数据、1 000条水库渗流数据。阈值分别取0、0.2、0.4、0.6进行训练，从准确率、总时间、每千行训练时间进行比较，结果如表1所示。

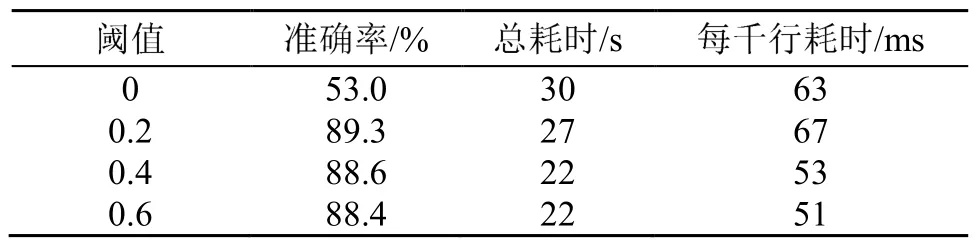
表1 不同阈值对算法结果的影响Table 1 The influence of different thresholds on the algorithm results

从表1能够看出，由于选取了更少的属性，随着阈值的增加，训练消耗的总时间在不断降低。准确率在阈值取0.2时达到最大，之后随着阈值的增大而减小。综合以上考虑，选择0.2为筛选ReliefF权重的阈值，去除6个属性，用排名前30的数据进行训练。

4.2.2 模型比较

不同模型的性能如表2所示，其中Marco-P为宏查准率，Marco-R为宏查全率，Marco-F1为宏F1值，这三者皆为多分类任务的评价指标。效果较好的模型包括梯度提升树模型、朴素贝叶斯模型、广义线性模型。由于朴素贝叶斯模型假设属性之间相互独立，故理论上准确率较高，但实际情况并非如此，主要因为声呐不同属性之间具有一定的相关性；广义线性模型对数据独立性要求较高，不独立的数据易导致标准差偏小，从而获得较高的理论准确率，但模型在实际使用时的准确率远低于理论准确率。而与梯度提升树模型相比，逻辑回归模型、快速大边界模型、决策树模型的各项指标较低。综上所述，梯度提升树模型在各项性能指标上均有较好的表现，说明本文提出的模型在声呐渗流检测结果分类方面具有良好的效果。

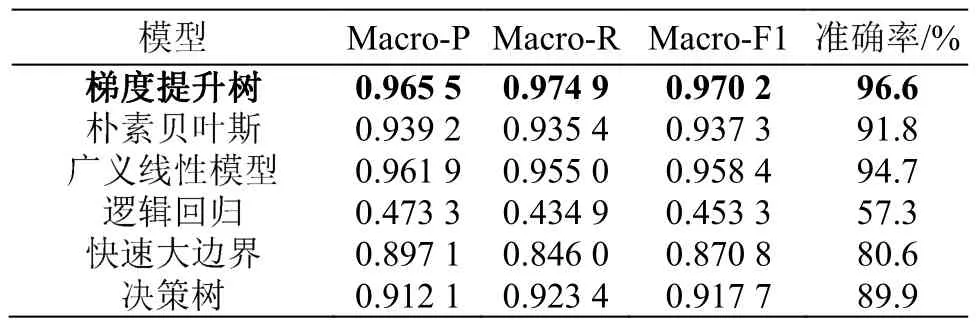
表2 不同模型的性能指标Table 2 Performance metrics of different models

4.2.3 模型分析

对得到的GBDT模型进行分析，可知不同属性对模型的贡献度不同，具体比例如图5所示。其中功率中位数占模型贡献度的 38.80%，振幅最大值占比 25.55%，时域整流平均值贡献占比 18.65%，振幅中位数贡献占比7.01%，其他属性对模型贡献度占比共为7%。

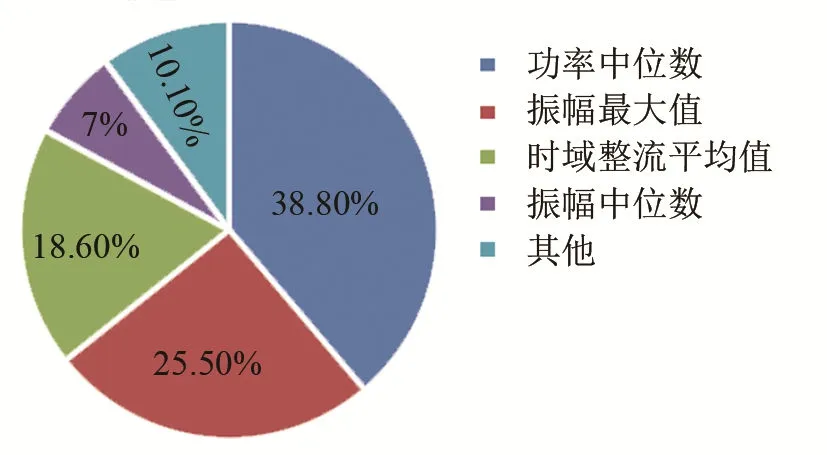
图5 不同属性对GBDT模型的贡献度Fig.5 The contribution of different attributes to GBDT model

功率中位数是声呐信号功率谱的直接体现；振幅最大值与振幅中位数可以较为准确地刻画出声呐信号频谱的振幅；时域整流平均值是声呐信号绝对值积分的平均值，能够较好地表现出声呐信号的时域的变化。利用决策树模型对上述属性进行分析，结果如图6所示，其中rl为水库渗流，pl为小孔渗流。

图6 GBDT模型分析过程Fig.6 Analysis procedure of GBDT model

综合看来，当阈值设置为0.384时，时域整流平均值能够区分水库渗流波形与其他两类渗流波形，其分布情况如图7所示；当阈值设置为0.005时，振幅中位数能够大致区分井孔渗流波形与噪声波形，其分布情况如图8所示。

由图7与图8可知，利用以上属性作为GBDT模型的分类指标具有较高的可信性，能够较好地区分三类波形。

图7 时域整流平均值分布情况Fig.7 The distribution of rectified mean values

图8 振幅中位数分布情况Fig.8 The distribution of the median amplitudes

5 结 论

本文提出了基于声呐信号与梯度提升树的声呐渗流检测结果分类模型。通过提取声呐数据的特征，对特征进行数据清洗与归一化，再利用ReliefF算法选取贡献权重大的特征，最后利用数据集训练出用于区分水库渗流、井孔渗流与噪声的梯度提升树模型。该模型在训练效率及分类精度方面有较好的表现。随着研究工作的深入和工程应用领域的扩大，我们将在更大的范围内采集到更多的工程应用声呐数据，在积累到一定程度后，尝试利用更好的大数据原解析手段与方法，使得声呐渗流测量技术的准确性、可靠性和抗干扰能力获得更大的提高，为众多渗流工程的风险控制与创新管理作出贡献。

致谢 感谢南京理工大学计算机工程学院为本文研究提供的技术支持。