声波作用下的单圆柱绕流及传热特性数值研究

姜 羽，姜根山，于 淼，杨延锋，孙建浩

(1. 华北电力大学数理学院，河北保定071003；2. 华北电力大学能源动力与机械工程学院，北京102206)

关键字：声波特性；圆柱绕流；漩涡脱落；强化传热

0 引 言

圆柱绕流是一种典型的绕流形式，具有广泛的工程实际应用背景，因此关于圆柱绕流和对流传热的问题也受到许多专家学者的关注[1-3]。

Saxena等[4]对比了稳定流和脉动流中矩形通道纵横比对圆管传热的影响，发现在低纵横比下圆柱会发生自然漩涡脱落和“锁定”脱落，抑制漩涡发散，换热效率下降。Mikheev等[5]对脉动流中圆柱绕流的漩涡脱落和换热进行了实验研究，分析了圆柱周围的流动模式，得到局部表面换热系数的分布与圆柱绕流流型和脉动振幅的关系，阐述了脉动流强化传热的机理。Gupta等[6]对中低雷诺数下幂律流体脉动流过加热圆柱时，层流强制对流的动量和传热问题进行数值模拟，得到幂律流体中，流体脉动对加热圆柱附近速度场及温度场的影响规律。Li[7]采用计算流体动力学的方法，研究了脉动流对错排换热管传热过程的影响，结果表明，低频和高振幅情况下传热系数较大，且脉动流对换热管的影响长度有限。Li等[8]还研究了单圆柱在脉动流中的传热特性，得到传热系数随脉动幅值、频率、斯特劳哈尔数以及雷诺数的变化规律。随着炉内声学技术的不断发展，对声波强化传热的研究也备受关注。许伟龙等[9]研究了强声波作用下单煤粉颗粒的传热特性，结果表明，声波的作用会促使颗粒表面时均努塞尔数增大。张东伟等[10]对超声强化传热进行研究，提出“空化链式反应”，解释了超声强化传热的机理，并通过数值模拟对产生强化传热的效果进行验证。

上述研究多是利用脉动流的机械作用或是超声波的作用强化传热效率，对可听声在圆柱绕流和传热中的研究还相对较少。崔淑媛等[11]利用数值分析的方法研究了管道绕流产生的声场特性，但没有研究声波对圆柱绕流的影响。于淼等[12]实验证明了声波可以诱导管内流场发生从层流到湍流的转化，该结果表明，声波对流场有明显的调制作用，但没有涉及对传热效率的影响。

本文对声波作用下单圆柱绕流和对流传热特性进行数值研究，分析层流状态下圆柱绕流漩涡的生长和脱落、圆柱表面压力系数、升阻力系数以及局部努塞尔数随声波频率和声压级的变化情况，得到声波参数对圆柱周围温度场和流场的影响规律，可以为声波在圆柱绕流和对流传热中的工程应用提供理论研究基础。

1 物理模型与控制方程

1.1 物理模型

考虑冷流体外掠单圆柱换热的情况，建立如图1所示二维数值计算模型。其中换热管管径D=40 mm，计算域高度为10D，宽度为27D。由于流体入口速度呈对称分布，为了触发涡流，在模型建立过程中将圆柱从流体流动中心做微小偏移，做不对称处理。采用正弦形式速度作为入口条件，U0是流体流速，Ug表示质点速度振幅。

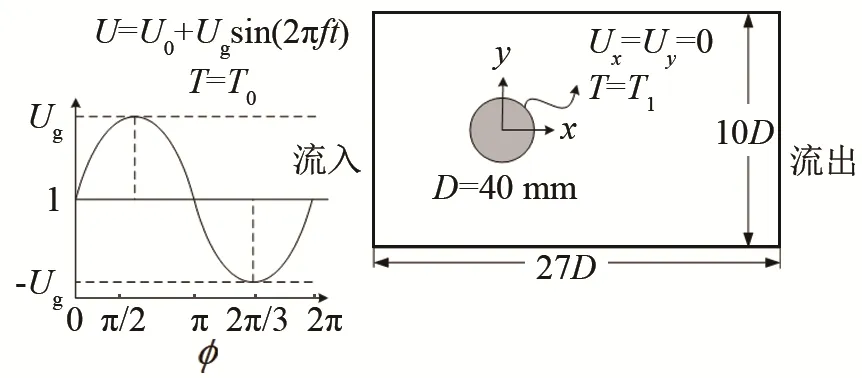
图1 数值计算模型Fig.1 Numerical calculation model

1.2 控制方程

对于二维不可压缩层流的对流传热问题，无声波作用时在柱坐标系下的连续性方程和动量方程如式(1)、(2)所示[13]:

1.3 边界条件

1.4 网格划分与独立性检验

利用COMSOL内置物理场控制的网格划分方法对模型进行网格划分，为保证数值计算结果的准确性，分别选取网格1、网格2、网格3、网格4四种不同类型的网格进行独立性验证，确保数值计算所选用的网格满足网格的独立性要求，对比四种网格下的平均阻力系数、斯特劳哈尔数Sr和平均努塞尔数Nu，计算结果如表1所示。

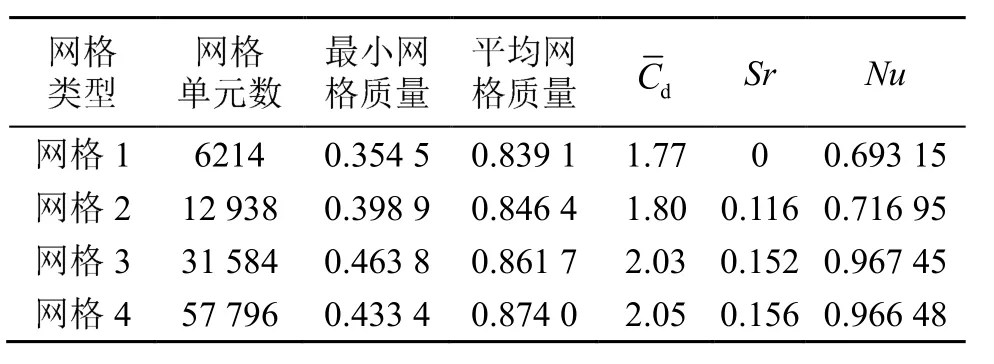
表1 网格独立性检验Table 1 Grid independence test

由表1可知，当网格密度达到网格3以上时，计算结果的误差缩小到 1% 以内，可以满足网格独立性要求。综合考虑网格质量以及节省计算资源，采用网格3的网格划分类型进行模拟计算。所得网格最大单元为 5.33 mm，小于所用声波波长的1/10，总单元数为31 584，最小网格质量为0.464，平均质量为 0.862，网格划分结果如图 2所示。图2(b)中色棒的数值越小表明网格质量越差，越接近1表明网格质量越好。

图2 网格划分结果Fig.2 Grid partition results

2 结果与讨论

2.1 声波特性对圆柱绕流漩涡分布的影响

图 3为有无声波作用时的漩涡分布图。由图3(a)可以看出，当无声波作用时，圆柱尾部有一个漩涡生成并按照一定的频率交替脱落；图3(b)可以看出当LSP=143 dB时，圆柱尾部产生两个漩涡，下涡拉拽迫使剪切层断裂，脱离圆柱体表面并发生破裂，同时形成新的上涡；图3(c)表明，当LSP=149 dB时，由于声能量的作用，漩涡刚产生便发生破裂，无漩涡交替脱落的现象产生。由图3可知，与无声波作用相比，声波作用使圆柱绕流剪切层变薄，Sr数减小，且声压级增大，圆柱绕流尾涡长度变短。

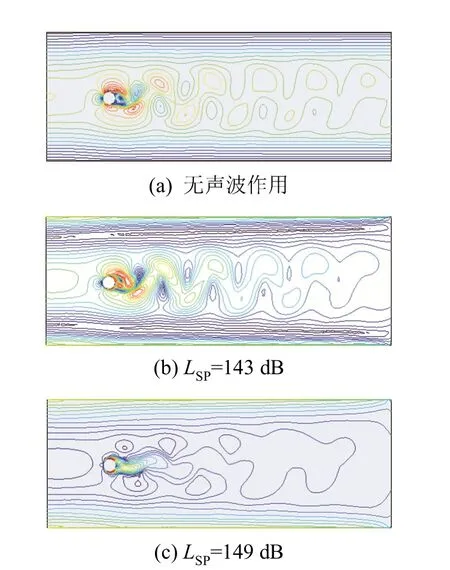
图3 不同声压级下圆柱绕流漩涡分布Fig.3 Vortex distribution around a cylinder under different sound pressure levels

图4为LSP=143 dB、f=30～80 Hz时，圆柱绕流漩涡分布。由图4(a)可以看出，当f=30 Hz时，圆柱尾部有稳定脱落的漩涡产生，上、下涡交替撕扯剪切层离开圆柱表面，尾涡形成的区域较长；在图4(b)中，f=50 Hz时，圆柱尾部仍然形成两列交替脱落的漩涡，漩涡破裂速度加快，尾涡长度变短；在图4(c)中，f=80 Hz时，漩涡尾迹仅为无声波作用时的一半。因此增大声波频率时，加快漩涡破裂，使漩涡尾迹变短。

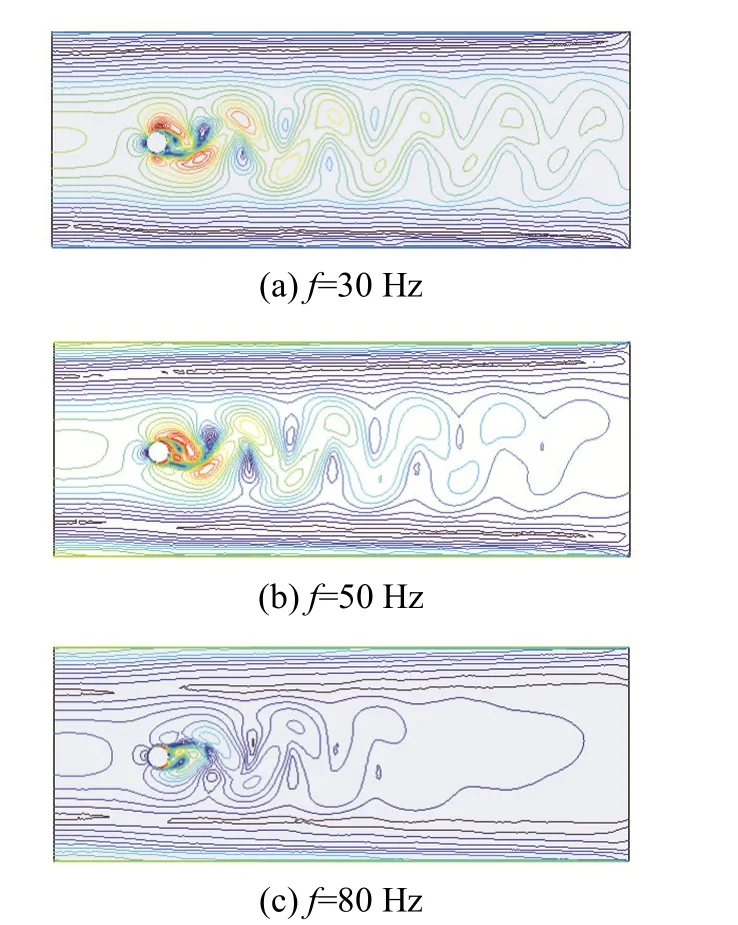
图4 不同频率下圆柱绕流漩涡分布Fig.4 Vortex distribution of flow around a cylinder at different frequencies

2.2 声波特性对圆柱表面压力系数的影响

流体绕圆柱运动时会对圆柱表面产生压力作用，利用压力系数Cp表示圆柱表面的相对压力分布，其定义为[6]

式中：P为圆柱表面压力；Pref为参考基准值(取θ=1 80°时的压力值)，θ=180°时，CP=0；ρ为流体密度。

图 5为无声波作用时圆柱表面压力系数分布图。A、C分别为圆柱上下表面流动分离点，沿迎流面顺时针方向取θ=0°为前驻点，θ=1 80°为后驻点。由图5中可以看出，无声场扰动时，圆柱表面最大压力系数为 5；在流动分离点之前，圆柱表面压力系数关于前后驻点呈对称分布，且由于流体流过圆柱导致流动截面缩小，流速加快，压力系数减小；在A、C点处边界层开始发生分离，压力系数出现回升；在75°≤ θ ≤ 2 85°范围内，是圆柱绕流尾迹区，该区域内尾涡发生脱离，由于逆时环量的存在叠加来流，导致上表面流速加快、下表面流速减慢，因此圆柱表面压力不再呈对称分布，而是以B点为分割点，圆柱下表面压力系数大于上表面压力系数，形成压强差。

图5 无声场作用圆柱表面压力系数Fig.5 Cylinder surface pressure coefficient without sound field

当对流体施加声波作用时，圆柱表面压力系数如图6所示，此时压力分布关于前后驻点对称，故取0°≤ θ ≤1 8 0°进行分析。图 6(a)为声波频率f=50 Hz、声压级LSP=123～149 dB时圆柱表面的压力系数。可以看出CP随声压级增大而增大。图6(b)为声压级LSP=143 dB、频率f=20～80 Hz时圆柱表面的压力系数，可以看出声波频率增大，CP同样增大。对比无声波作用下的压力系数可以发现，当存在声波激励时，声压作用于圆柱使圆柱表面压力明显增大，同时随着θ的增大，圆柱表面压力系数递减，在θ=1 80°处最小。

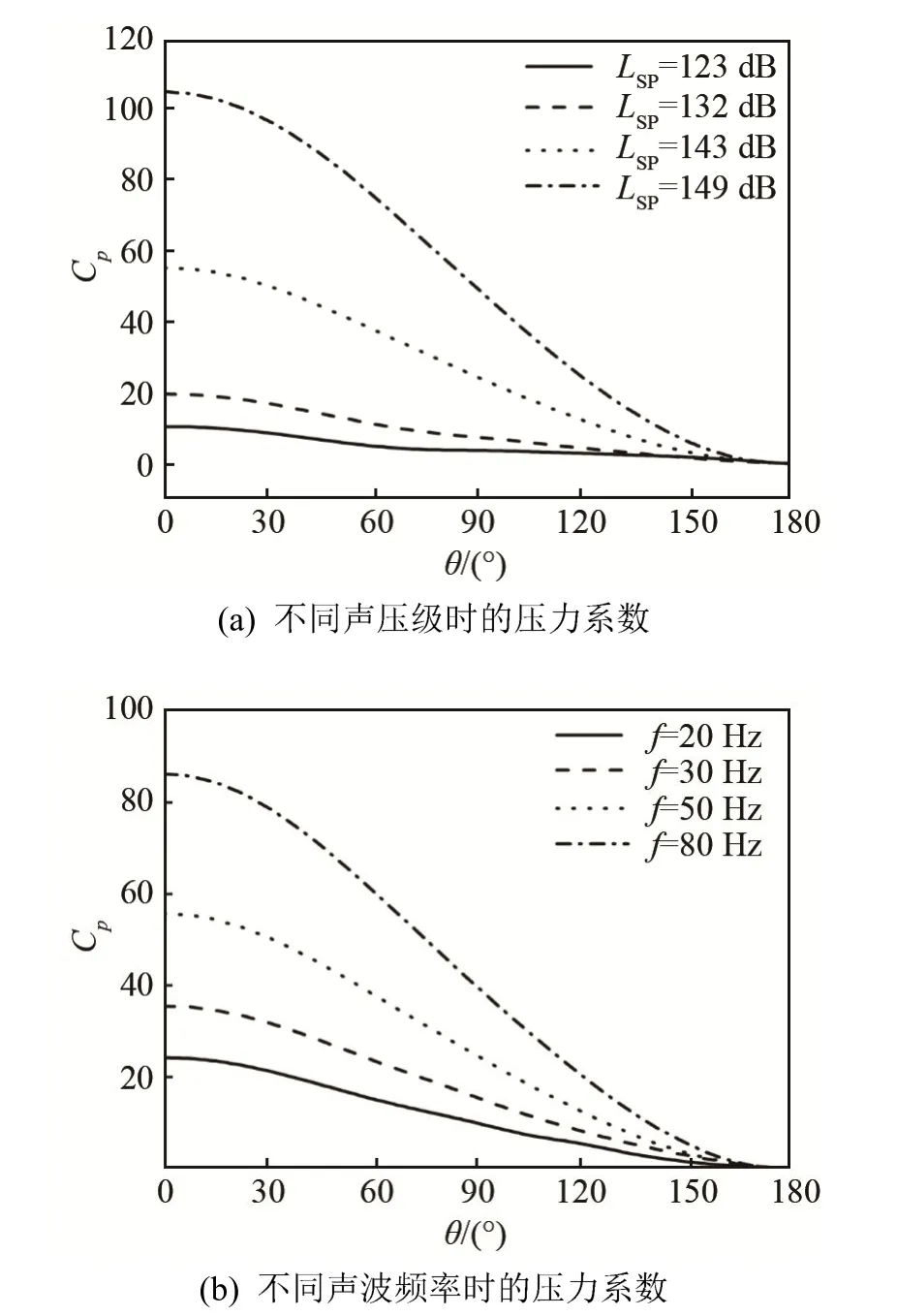
图6 声波作用下圆柱表面压力系数Fig.6 Cylinder surface pressure coefficient under the action of sound wave

2.3 声波作用对圆柱表面升阻力系数的影响

黏性流体绕物体运动时，物体表面会受到压力和摩擦力作用，两者合力可以分解为沿来流方向上的绕流阻力FDF以及垂直于来流速度U0方向上的绕流升力FDL，合力 FD= FDF+ FDL。S表示圆柱表面积，则绕流阻力系数和升力系数定义为

图7为有无声波作用圆柱表面阻力系数。从图7中可以看出，无声波作用时，圆柱绕流阻力系数最大值约为 2.7，呈正弦形式变化，当对流体施加LSP=143 dB、f=50 Hz的声波扰动之后，圆柱绕流阻力系数可达45，仍然呈正弦形式，频率与声波频率一致。图8为有无声波作用时升力系数的变化情况，可以看出声波的作用使升力系数由正弦形式变为非正弦的周期性变化，振幅增大。升力指圆柱表面垂直于流速方向的力，在无声波作用时由压力和摩擦力提供。当将声波作用于稳定流体之后，圆柱表面除了受流体压力和摩擦力的作用，还受声波压力作用，因此圆柱绕流升、阻力系数发生变化。

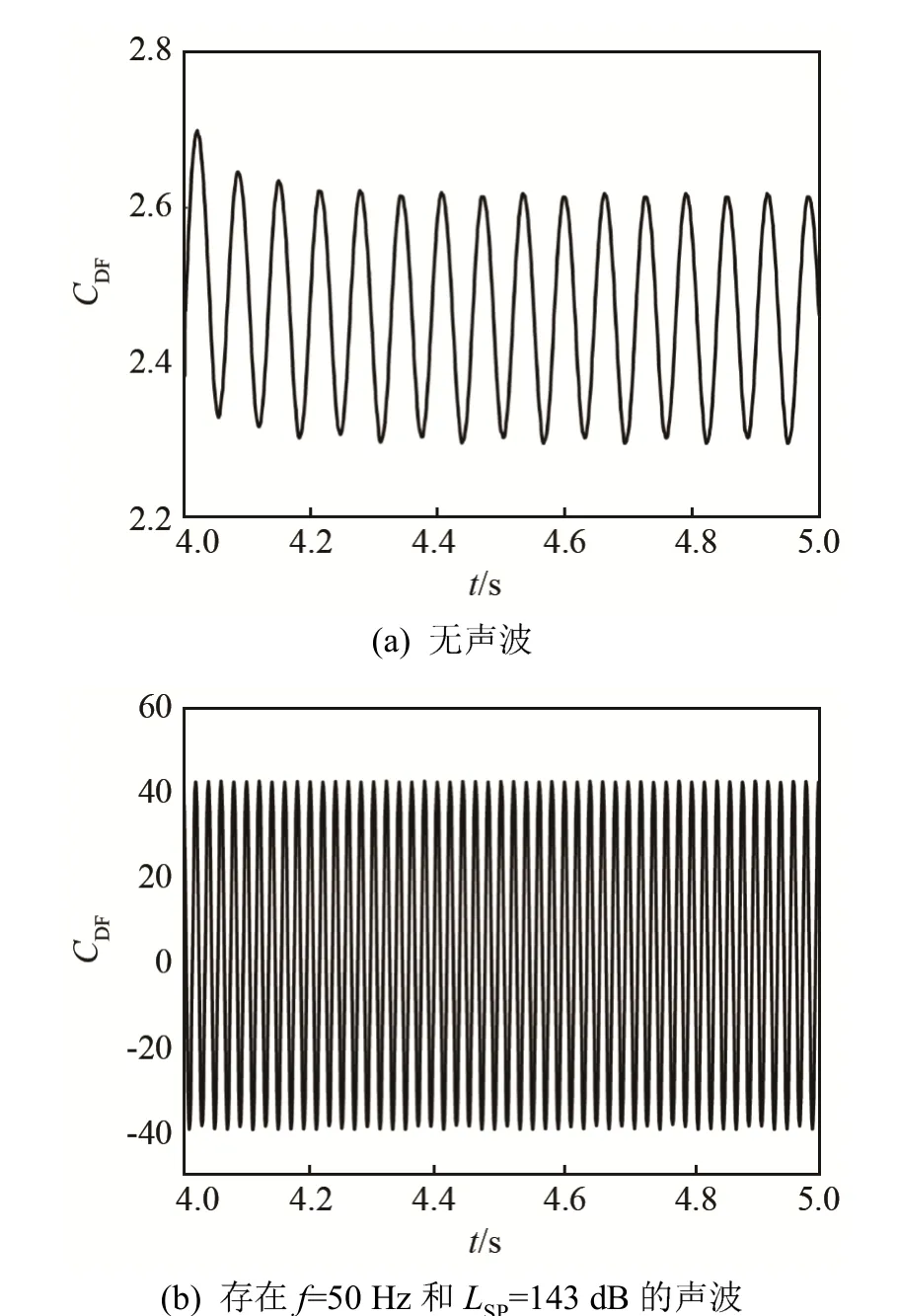
图7 圆柱表面阻力系数Fig.7 Cylinder surface resistance coefficient

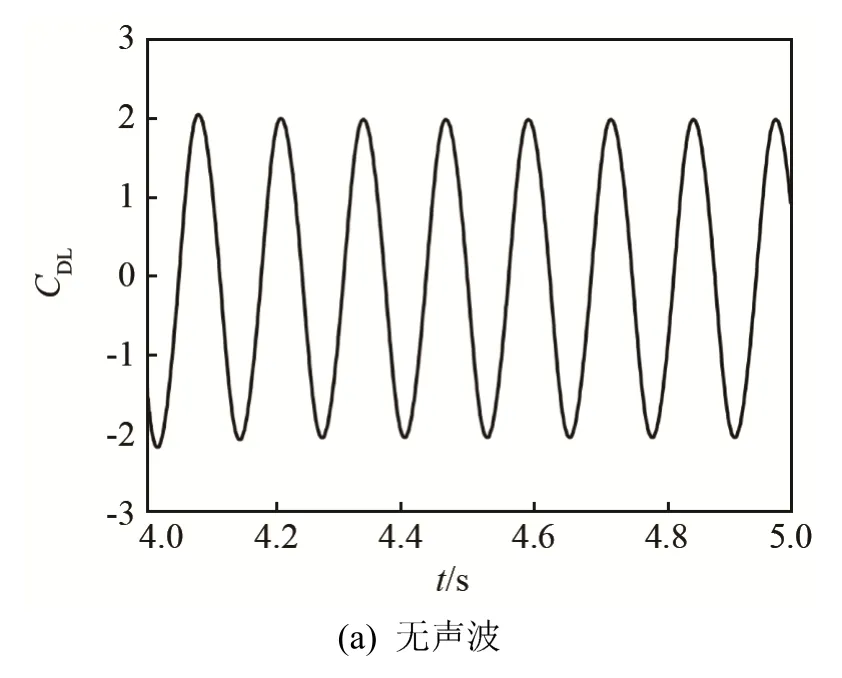
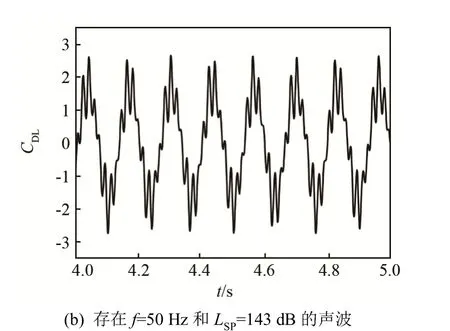
图8 圆柱表面升力系数Fig.8 Cylinder surface lift coefficient

2.4 声波特性对斯特劳哈尔数的影响

圆柱直径、漩涡脱落频率、来流速度之间的关系为

式中：D表示圆柱直径；fs表示漩涡脱落频率；U0表示流场来流速度。

图 9为f=50 Hz、不同声压级作用下圆柱绕流升力系数的频谱图。由图 9(a)可知，声压级LSP=123 dB时，圆柱绕流升力系数的频谱图只存在一个较明显的主频，即为漩涡脱落频率；由图9(b)～9(d)中可以看出，随着声压级的增大，升力系数频谱图出现多个高阶谱峰，其中振幅最大的主频为漩涡的脱落频率fs，其他频率为声波频率与漩涡脱落频率叠加所得。

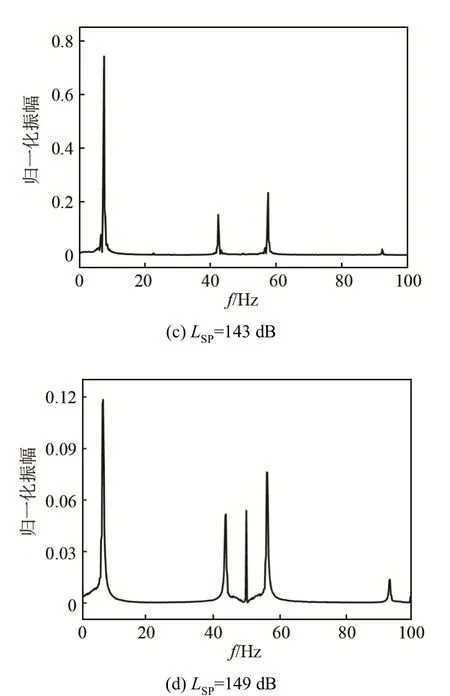
图9 不同声压级下升力系数频谱图Fig.9 Spectrograms of lift coefficient at different sound pressure levels

表2为各声压级下漩涡的脱落频率，从表2中可以看出，当f=50 Hz、LSP=123～149 dB时，Sr数随声压级增大而减小，这是因为声压级增大，声能量增大，加快漩涡的破裂，漩涡脱落频率减慢。同时漩涡破裂会破坏热边界层，可以提高圆柱绕流的对流传热效率。

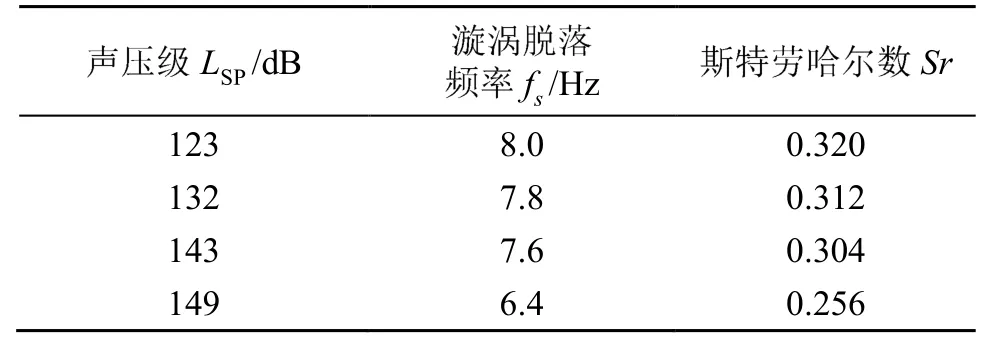
表2 不同声压级下漩涡脱落频率Table 2 Vortex shedding frequencies at different sound pressure levels

图10为LSP=143 dB、f=20～80 Hz时，圆柱绕流升力系数频谱图。由图 10中可以看出，除了漩涡脱落频率之外，同样存在高阶谱峰，且随着声波频率的增大而增大。将不同声波频率下的漩涡脱落频率记录在表3中，可以看出随着声波频率的增加，Sr增大，圆柱绕流漩涡的脱落频率加快，可以有效促进换热管壁与流体之间的热量传递。当声波频率f ＞100 Hz时，漩涡脱落频率fs与作用于流体的声波频率一致，说明此时漩涡的脱落主要受声波频率的影响。在此情况下会引起圆柱共振，造成管壁疲劳损伤，在实际应用中应避开相应的频率。

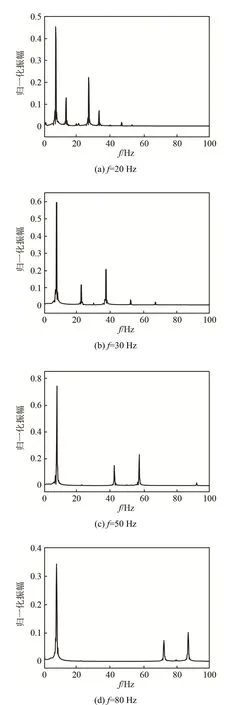
图10 不同声波频率下升力系数频谱图Fig.10 Spectrograms of lift coefficient at different acoustic frequencies

表3 不同声波频率下漩涡脱落频率Table 3 Vortex shedding frequencies under different acoustic frequencies

2.5 声波特性对圆柱表面局部努塞尔数的影响

为研究声波对圆柱对流传热的影响，设定圆柱管壁为恒温条件：

用垂直于圆柱表面的温度梯度表示局部努塞尔数Nuθ[6]：

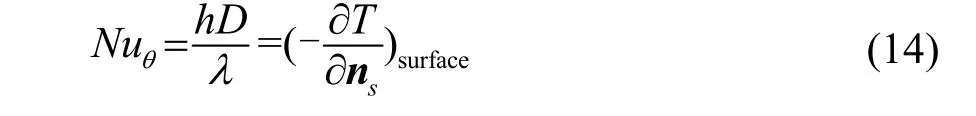
其中：ns为圆柱表面法向量，方向垂直于圆柱表面向外，h为表面传热系数，λ为流体导热系数。

图 11为声波频率和声压级对 Nuθ的影响。图11(a)为LSP=143 dB、f=20～1 000 Hz时圆柱表面局部对流传热系数Nuθ的分布情况。从图11(a)中可以看出，在前驻点处Nuθ的值最大，因为前驻点处流体对圆柱作用力最大，传热推动力最强；在绕圆柱运动过程中，随着热边界层的增长，Nuθ逐渐减小，在流动分离点处达到最小值；在流动分离点之后，由于漩涡的脱落，Nuθ变大，在θ= 1 80°时，Nuθ达到极大值。在流动分离点之前，局部努赛尔数Nuθ随频率增大而增大；在圆柱尾迹区局部努塞尔数随频率先增大后减小；频率达到1 000 Hz时，Nuθ明显增大，平均努塞尔数Nu较f=20 Hz时提高17%。图 11(b)为 f=50 Hz、LSP=123～149 dB时局部努塞尔数Nuθ分布情况。从图11(b)中可以看出，随着声压级的增大，在110°≤ θ ≤ 2 50°范围内，局部努塞尔数Nuθ先增大后减小。这是因为当有声波作用时，声能量对流体的激励作用会诱导其做周期性运动，破坏流动边界层和热边界层，同时形成漩涡促进边界层内部的对流。随着声压级的增大，声能量对流体的作用越强，促进尾迹区热量交换；但是当声压级LSP＞143 dB时，声波作用使流体流速大幅度增加，同时加快漩涡破裂，流体与管壁接触时间过短，传热效率下降。

图11 声波频率和声压级对Nuθ的影响Fig.11 The influences of sound wave frequency and sound pressure level on Nuθ

3 结 论

通过数值模拟研究了声波对单圆柱绕流及对流传热的影响，对计算结果进行分析可以得到如下结论：

(1) 在声波作用下，圆柱表面压力系数分布关于前后驻点对称，在0°≤ θ ≤1 8 0°范围内，圆柱表面压力系数Cp随的θ增加而递减，随声压级和声波频率的增大而增大。

(2) 当存在f=50 Hz、LSP=143 dB的声波时，与无声波作用时相比，声波作用于圆柱表面使圆柱绕流阻力系数CDF和升力系数CDL振幅变大；升力系数CDL由无声波作用时的正弦形式变化变为非正弦的周期性变化。

(3) 斯特劳哈尔数Sr随声压级增大而减小，随声波频率增大而增大；当声波频率f ＞100 Hz，漩涡脱落频率与声波频率一致。

(4) 声波频率和声压级的增加会促进圆柱周围流体与管壁的热量交换，但当声压级LSP＞143 dB时，局部努塞尔数Nuθ随声压级增大而减小，此时传热效率下降。