问渠那得清如许 为有源头活水来——从一道高考题的溯源与探究中谈解析几何题的命制

安徽 万 胜

(作者单位：安徽省芜湖市第一中学)

每年的高考真题都是命题者的智慧结晶，而每年的解析几何高考真题，一般都具有初等几何或高等几何背景.笔者对2020年高考全国卷Ⅰ理科中的解析几何第20题的题源进行分析与探究，分别从初等几何和高等几何的范畴思考本题，从具体实例中揭示研究圆锥曲线性质的初等几何与高等几何的两种思考方法，同时以此来观察高等几何与初等几何的联系，从该高考题背景中探寻规律，揭示试题题源，命制新题，以期对一般的解析几何试题的命制规律具有一定的指导作用，供教师参考.

一、试题呈现

(Ⅰ)求E的方程；

(Ⅱ)证明:直线CD过定点.

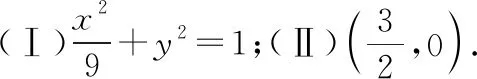
二、初等几何、变换溯源

事实上，题目1中体现了关于阿波罗尼斯圆的命题，是其在伸压变换下，由圆变为椭圆所对应的结论，其中有如下命题与结论：

命题1：如图1，设AB是圆O的一条直径，点P是与AB垂直且与圆O相离的定直线上的任意一点，设直线PA,PB与圆的另外两个交点分别为C,D，则直线CD过直径AB上的定点S.其逆命题也成立.

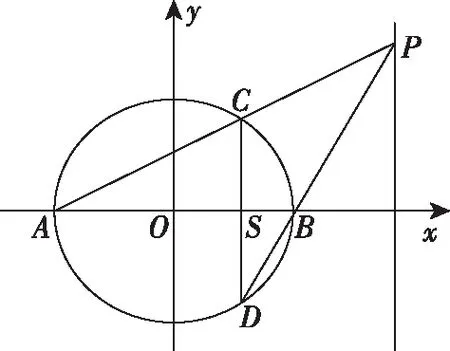
图1

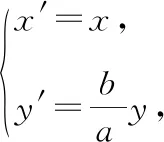
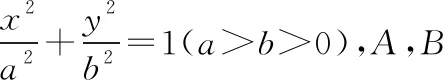
(注：为方便比较，引用上述命题与结论时，部分字母有所调整；同时为了符合人教版教材编写内容，本文中变换呈现方式也有所调整.)

显然，追根溯源，2020年全国卷Ⅰ理科第20题(Ⅱ)是本结论的特殊情况.这种基于椭圆与圆的伸压关系，回到圆这样的初等几何基本图形，利用平面几何中圆的性质衍生出椭圆相关结论(事实上还可以类比椭圆的性质，进一步类比产生双曲线与抛物线的类似性质)，不失为一种较好的研究圆锥曲线性质的方法.

三、延伸探究、思考本质

1.特殊到一般、实验探索

欣赏着如此美妙的初等几何性质与本题的关系，笔者仍然感到美中不足，该题中的A,B两点为椭圆长轴端点，能否推广到一般情形呢？如图2，即若AB为椭圆E的任意一条弦，PA与E的另一交点为C，PB与E的另一交点为D.直线CD过定点吗？

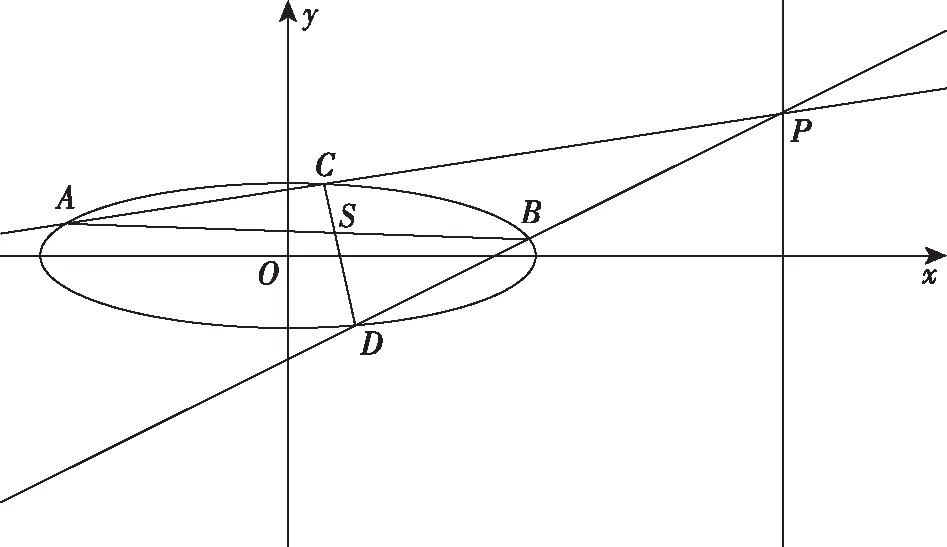
图2

能否从该椭圆伸压变换前所对应的圆出发，若AB为该圆的任意一条弦，得到性质，进而产生椭圆相关结论呢？

考虑到从圆的角度出发，用初等几何方法来推导的困难性，以及从椭圆出发运算的复杂性，况且该结论的正确性也具有未知性.

为此，笔者想到先用信息技术辅助验证，因而不妨选择椭圆用几何画板软件进行作图验证，如图3，从直线族CD的包络图形可知，直线CD并不过某定点.

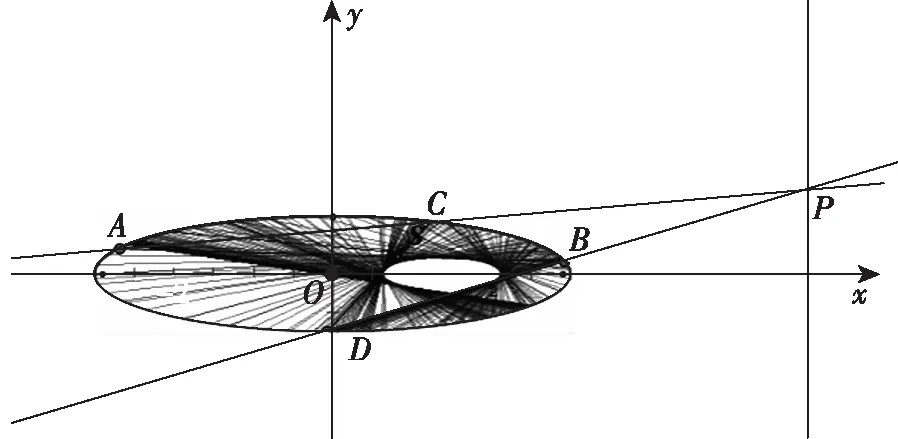
图3

2.高等几何、本质溯源

为了揭示本题所蕴含的内在规律，给出如下椭圆中的一般性质：

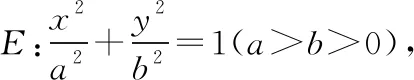
图4

由此易知，结论1为命题2的特殊情形.同时，易知AD,BC的交点Q也在该极线l上，从而可以仅仅利用直尺作出点S关于该椭圆的极线l(如图5及图6).

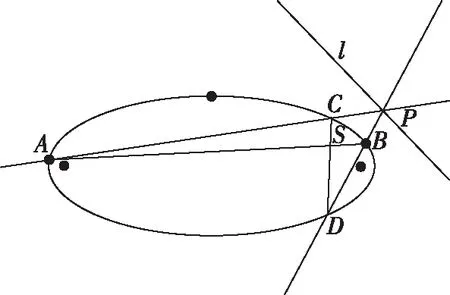
图5

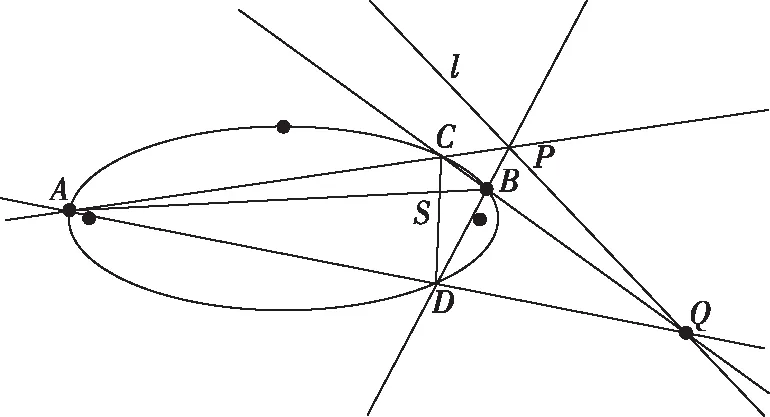
图6

3.理解本质、直尺作图

从高等几何的范畴看，点列与线束之间的射影是对应的.所以只需作出极线l上点列关于该椭圆所对应的极线束的交点，也是该极线l所对应的极点，即本题中的定点.当然考虑极线l上P,Q两点所对应的极线p,q的交点即可.

如图7，对于椭圆外一点P，仿照图5和图6作图方法：过点P作椭圆E的两条割线l1,l2交椭圆E于点A,B和C,D，设AC,BD的交点为T，AD,BC的交点为R，则点P关于椭圆E的极线p即直线RT.同理可以作出点Q的极线q，这样两直线p,q的交点即为所求极点.

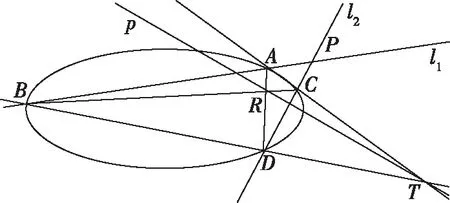
图7

更为奇妙的是，如图8，对于该椭圆外一点P，其极线p与椭圆E交于两点M,N.易知点M的极线必过点P，而由命题2可知椭圆上的点的极线即为该点处的切线，所以直线PM与椭圆E相切，同理：直线PN与椭圆E相切.这样，既给出了椭圆外一点P关于该椭圆的极线作法(只需过点P作出椭圆的两条切线，两切点连线即为极线)，同时该过程也给出了仅仅用直尺作出椭圆切线的方法.

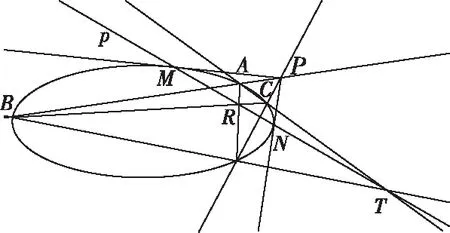
图8

这样，我们可以用高等几何知识为理论依据.如图9，用类似于图9的方法仅仅用直尺由圆外一点P作出该圆的两条切线PM,PN，进而得出点P关于该圆的极线MN；如图10，在直线l取异于点P的一点Q，作出其关于该圆的极线M1N1，则直线MN与直线M1N1交点S即为直线l关于该圆的极点.

图9 图10

四、理论实践、编制新题

基于以上论述，完善笔者的猜想，可将2020年全国卷Ⅰ理科第20题推广，进而可以编制新的试题.

对于题目1，我们试图修改题中已知直线AB的位置，利用潜在的极点与极线的对应关系，通过极线上动点P的运动产生动直线CD，进而由动直线CD所过的定点得到该极线所对应的极点.

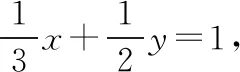
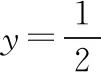
这样可以编制如下关于圆的试题.

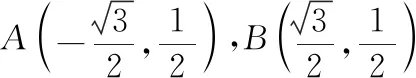
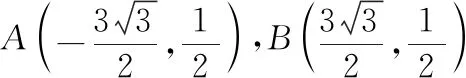
图11

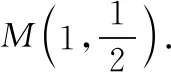
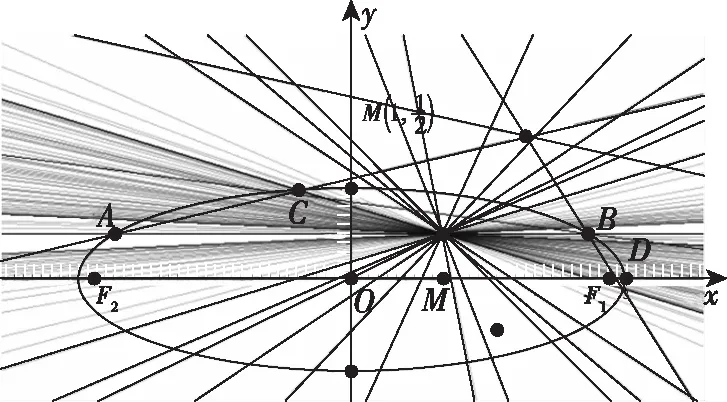
图12

当然，本题可推广至一般情形.

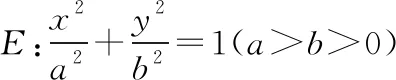
五、归纳过程、清晰规律

追根溯源，才能站得高，看得清晰.以上探究过程蕴含着2020年全国卷Ⅰ理科第20题的背景.同时，也揭示了高中平面解析几何试题的一类编制方法：一方面可以从初等几何图形的性质中衍生出圆锥曲线相关性质；另一方面可以用高等几何的知识作为理论依据，拓宽初等几何研究的思路，在更高的范畴内讨论问题，理解问题，加深对于初等几何的理解和概括，从而对于其中的问题理解更加清晰，再利用类比思想，恰当变换从而命制解析几何试题.