基于轨迹意识的试题研究
福建 黄清波 黄晓琳
(作者单位:福建省南安国光中学)
近几年各级各类考试轨迹问题的命题不再局限于解析几何,而是转变为在知识的交汇处命题,将平面几何与解析几何、三角函数、立体几何、平面向量等融为一体,从而使题目更加新颖、灵活,符合考试说明中提出的“以数学知识为载体,测量考生将知识迁移到不同情境的能力,从而检测考生已有的潜在学习能力”.本文结合典例从几个视角进行剖析,引导考生思考如何在解题中建立轨迹意识.
一、轨迹意识在解析几何中的应用
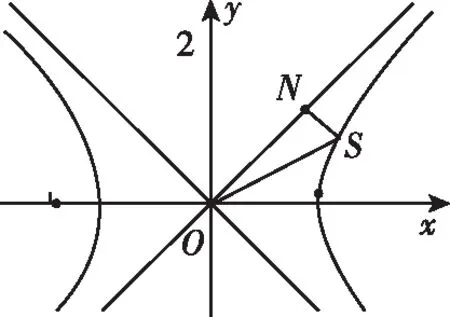
【典型例题】(2021·衡中全国第二次联考·12)在一张纸上有一圆C:(x+2)2+y2=r2(r>0)与点M(m,0)(m≠-2),折叠纸片,使圆C上某一点M′恰好与点M重合,每次折叠都会留下一条直线折痕PQ,设折痕PQ与直线M′C的交点为T,则下列说法正确的是( )
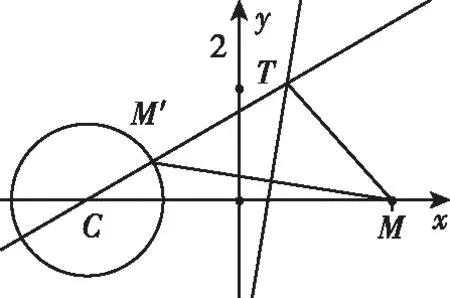
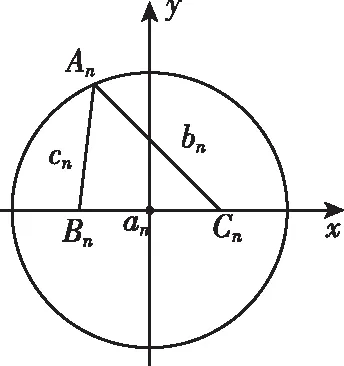
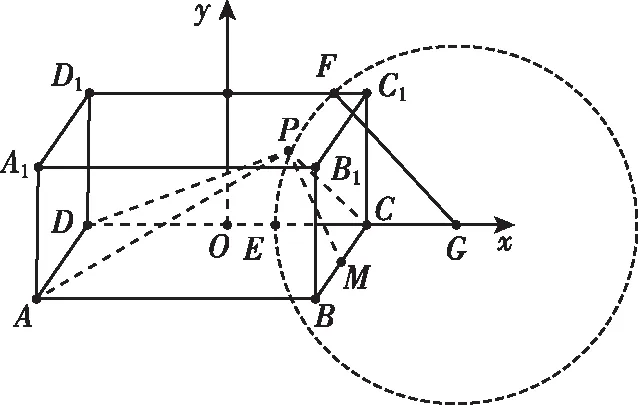
A.当-2-r C.当m=2,1≤r≤3时,点T的轨迹对应曲线的离心率取值范围为[2,4] 【命题意图】本小题考查轨迹问题、圆锥曲线的定义、圆锥曲线的性质与方程、命题真假判断等基础知识,考查抽象概括能力、推理论证能力,考查数形结合思想、函数与方程思想、化归与转化思想,考查数学抽象、直观想象、逻辑推理、数学运算等核心素养. 【思路探析】对于A:根据题意可得|TM|+|TC|=|CM′|=r>|CM|,则点T的轨迹是以C,M为焦点的椭圆,即可判断A是否正确; 对于B:根据题意可得‖TM|-|TC‖=|CM′|=r<|CM|,则点T的轨迹是以C,M为焦点的双曲线,其中2a=r=1,2c=CM=4,进而可得双曲线方程,即可判断B是否正确; 对于C:根据题意可得点T的轨迹是以C,M为焦点的双曲线及方程,进而可得离心率,即可判断C是否正确; 对于D:根据题意可得T的轨迹方程为x2-y2=2,即可判断C是否正确;设S(p,q),直线SN的方程, 它与y=x的交点N的坐标,即可计算S△SNO是否为定值,即可判断D是否正确. 解:当-2-r 【反思】一般情况下,在轨迹问题中,所有的动点等动元素都是在一个不变的背景或框架下运动的,或者说动点轨迹一般都是确定的,有的题目直接交代了,属于“显轨迹”,有的题目没有明确交代,可称为“隐轨迹”,发现这些轨迹路径,这类问题将不再无迹可寻. 破解此类问题的关键:一是对图形变化要有动态的认识——通过对图形结构的理解、探索,能够建立良好的形与数的联系,迅速挖掘隐藏的轨迹,找到轨迹就找到了要害,因此解题要树立用轨迹思想解决动态问题的意识,并且反复强化,达到熟能生巧的地步;二是熟练掌握求轨迹的方法,如熟悉几类特殊曲线定义的定义法、求出符合各条件对应点轨迹的公共部分的交轨法、含参的动点坐标消参的参数法、直接将条件翻译成等式并化简得到的直译法等. 所以A为BE的中点, 过C作CF⊥AB,垂足为F. 因此点E的轨迹方程为(x-1)2+y2=5. 【典型例题】已知△ABC中,角A,B,C对应的边分别为a,b,c,记△ABC的面积为S. 【命题意图】本小题以三角形为载体,主要考查正、余弦定理、面积公式、基本不等式等基础知识,考查逻辑推理、直观想象、数学运算等核心素养. 【思路探析】本题如果能够理解三角形中点、线的运动和静止的关系,利用轨迹的思想数形结合地解决问题,将能出奇制胜、化繁为简. 显然当A位于该弧的中点A′处时,△ABC面积最大. 此时,△ABC是正三角形, (Ⅱ)如图,以BC的中垂线所在的直线为y轴建立平面直角坐标系. 化简得(x-3)2+y2=8(y≠0). 【反思】解决这类问题的关键在于抓住边或角的某种定量关系,探索出三角形某个顶点运动的轨迹,用“形”的观点去解决所要研究的问题.这种数形结合的解题方法,使问题的求解更加直观形象. A.{Sn}为递增数列 B.{Sn}为递减数列 C.{S2n-1}为递增数列,{S2n}为递减数列 D.{S2n-1}为递减数列,{S2n}为递增数列 解:因为an+1=an,故数列{an}为常数数列, 所以bn+cn=2a,即{bn+cn}也为常数列. 在△AnBnCn中,BnCn=an=a,AnBn+AnCn=bn+cn=2a. 故An是以Bn,Cn为焦点,长轴长为2a的椭圆, 设An(xn,yn),由椭圆的焦半径公式有bn-cn=-2exn,其中e为椭圆离心率. 【命题意图】本小题以三角形为载体,主要考查平面向量及其应用、圆的相关知识等,考查逻辑推理、直观想象、数学运算等核心素养. 解:如图,以AB的中点O为坐标原点,AB所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系,则A(-1,0),B(1,0),设点P(x,y), 即(-1-x)(1-x)+y2-2λ+1=0. 化简得x2+y2=2λ(λ>0). 过点O作OM⊥AC,垂足为点M. 由题意知,线段AC与圆x2+y2=2λ有两个交点, 【命题意图】本小题以四棱柱为载体,考查点线面间的位置关系,涉及动点的轨迹问题等,考查化归与转化思想,考查直观想象、逻辑推理和数学运算核心素养,体现基础性与创新性,有一定难度. 解:如图,取B1C1的中点为E,BB1的中点为F,CC1的中点为G, 已知∠BAD=60°,直四棱柱ABCD-A1B1C1D1的棱长均为2, 又四棱柱ABCD-A1B1C1D1为直四棱柱,BB1⊥平面A1B1C1D1,BB1⊥D1E, 且BB1∩B1C1=B1,因此D1E⊥侧面BCC1B, 设P为侧面B1C1CB与球面的交线上的点,则D1E⊥EP, 【反思】解决这类问题主要有两种方法:一种是几何法,化立体为平面,通过几何证明或几何关系分析,由几何图形的定义,确定动点轨迹;另一种是代数法,化几何为代数,通过向量的表示和运算将原问题转化为代数问题,得到动点的轨迹方程,根据方程形式判断轨迹. 【变式】(2020·安徽省合肥市三模理·10)在长方体ABCD-A1B1C1D1中,AB=AD=6,AA1=2,M为棱BC的中点,动点P满足∠APD=∠CPM,则点P的轨迹与长方体的面DCC1D1的交线长等于( ) 【思路探析】依题意画出图形,由角的关系得到边的关系,建系后由求轨迹方程的方法求得P的轨迹,进而求得交线长. 解:如图,当P在平面DCC1D1内时, AD⊥平面DCC1D1,CM⊥平面DCC1D1, ∠APD=∠CPM. 在Rt△PDA与Rt△PCM中,AD=6,所以MC=3, 得PD=2PC. 在平面DCC1D1中,以DC所在直线为x轴,以DC的垂直平分线为y轴,建立平面直角坐标系, 则D(-3,0),C(3,0), 整理得(x-5)2+y2=16.所以点P的轨迹是以G(5,0)为圆心,半径为4的圆. 《普通高中数学课程标准(2017年版2020年修订)》提出“在高中数学的教学中,要注重数学的不同分支和不同内容之间的联系”,高考大纲也提出了数学整体性和综合性的要求,轨迹问题利用基本对象的几何要素、几何性质的转化,建立数与形的联系,将立体几何、平面几何与解析几何等融为一体,凸显了知识的应用性,更好地实现问题的解决.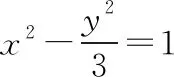
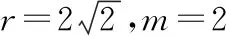



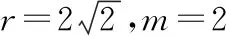
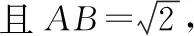


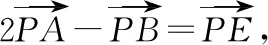

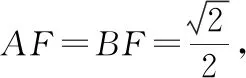
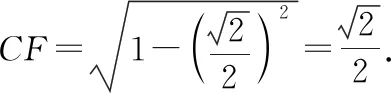

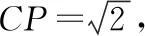

二、轨迹意识在解三角形中的应用


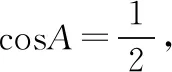
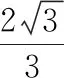
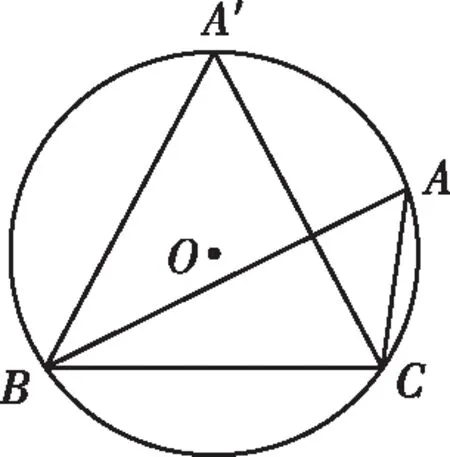
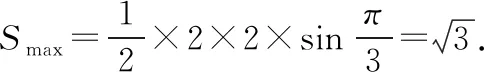
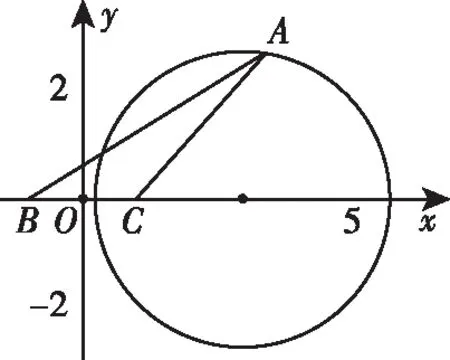
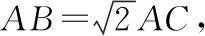

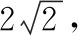
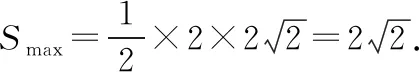
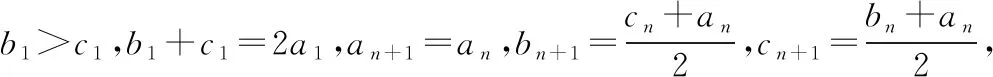
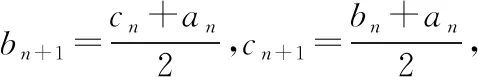

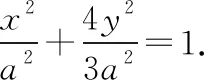
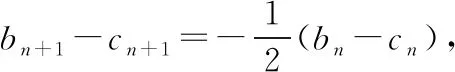

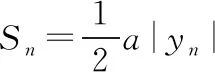
三、轨迹意识在平面向量中的应用



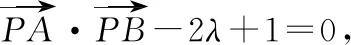




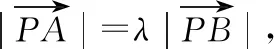


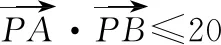

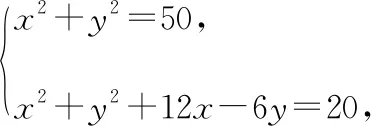
四、轨迹意识在立体几何中的应用

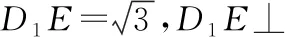




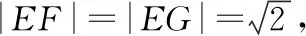
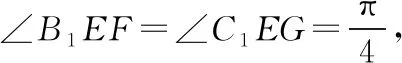



五、解题感悟


