新课标、新高考、新教材背景下教育质量检测工具的跨区域研发项目成果展示

山西 李小丽 江苏 胡道国 辽宁 闫海鹏

(作者单位：山西省平遥中学校 江苏省宿迁市沐阳如东中学 天津市翔宇力仁学校)

【试题一】对于函数f(x)，若存在常数a≠0，使得x取定义域内每一个值，都有f(x)=f(2a-x)，则称f(x)为准偶函数.下列函数中是准偶函数的是________(把所有满足条件的序号都填上).

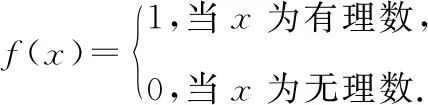
【试题解析】

剖析新定义：即函数f(x)是轴对称图形，且至少存在一条非y轴的对称轴.

①只有当a=0时，满足f(x)=f(2a-x)，所以f(x)不是准偶函数；

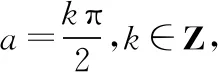
③设g(x)=-x2+2|x|，h(x)=-x2+2x-1+2|x-1|，易得h(x)=g(x-1)，因为g(x)是偶函数，关于y轴对称，所以p(x)=2g(x)也是偶函数，而f(x)可看成是由p(x)向右平移1个单位长度所得，所以f(x)的图象关于x=1对称，即f(x)=f(2-x)；

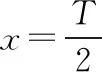
综上，满足条件的是②③④.

1.命题依据

【学科型专业依据】本题对应高考填空题中14、15题的位置，对知识点、难度的考查类似，基本初等函数以及以基本初等函数为载体的复合函数和分段函数的性质是高考中的高频考点.

【教育测量学依据】本题以山西省平遥中学高三年级学生为测试样本，难度系数0.7，符合高考题的难度区间，是一道很好的创新题.

【教学经验型依据】

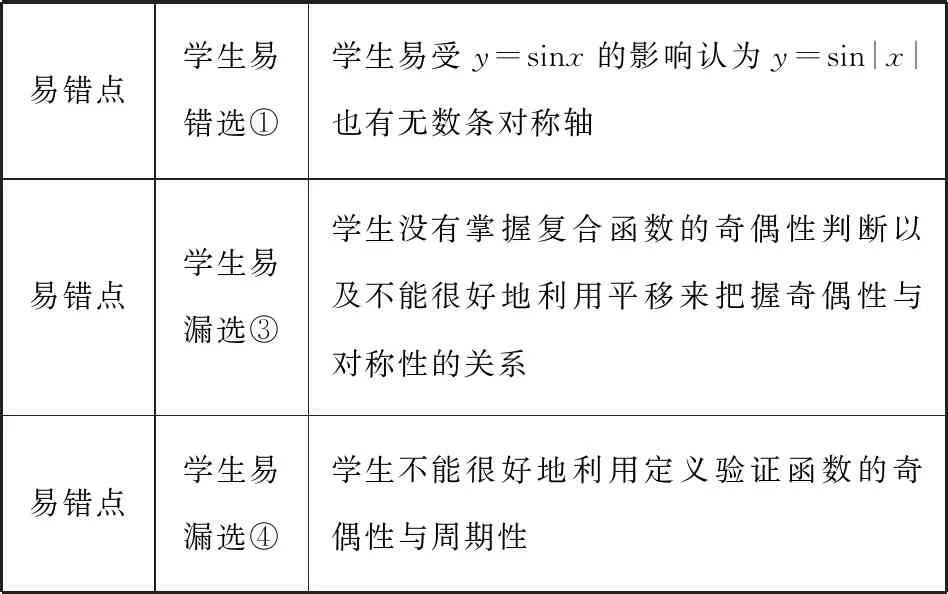
易错点学生易错选①学生易受y=sinx的影响认为y=sin|x|也有无数条对称轴易错点学生易漏选③学生没有掌握复合函数的奇偶性判断以及不能很好地利用平移来把握奇偶性与对称性的关系易错点学生易漏选④学生不能很好地利用定义验证函数的奇偶性与周期性

2.命题意图

本题以一个新定义为载体，考查学生获取新知识的能力和对新问题的探究能力，挖掘数学问题的本质：函数的奇偶性，对称性，把握奇偶性与对称性的区别与联系(可通过函数的平移实现转化)；奇偶性、对称性、周期性三者是知二推一的关系.考查二次函数、三角函数、指数函数等基本初等函数与以绝对值函数为代表的分段函数的图象与性质；考查复合函数的奇偶性与对称性；另外还引进高等代数中一个特别重要的分段函数——狄利克雷函数，由此让学生深刻体会奇偶性、对称性、周期性的严格定义.提高学生对知识的整合运用能力，考查了数学抽象与逻辑推理的学科素养.

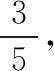
A.40 408 B.40 432

C.40 420 D.80 840

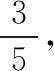
如果右焦点射出光线不沿长轴方向的话，经反射后汇聚到左焦点，相当于从左焦点再次射出光线，依然不沿长轴方向，经反射后汇聚到右焦点，即光线第一次回到右焦点经过的路程为4a即40 cm，故第2 021次回到该焦点所经过的路程长为2 021×40=80 840 cm；

如果右焦点射出光线沿长轴方向的话，分成两种情况：第一类是经右顶点反射直接回到该焦点，光线经过路程为2a-2c即8 cm，第二类是路过左焦点经左顶点反射回到左焦点再次回到右焦点，光线经过的路程为2a+2c即32 cm.若按照第一类情况，光线第2 021次回到该焦点所经过的路程1 010×32+1 011×8=1 010×40+8=40 408 cm；若按照第二类情况，光线第2 021次回到该焦点所经过的路程1 011×32+1 010×8=1010×40+32=40 432 cm，故选ABD.

1.命题依据

【学科型专业依据】

教无定法，考无定势，新高考下已无考试大纲，对学生的知识考查已回归课本，注重定义本质的理解，性质内涵的研读，知识链式的构建.命题的角度已呈现发散式、开放式、链条式等诸多特征.学科的核心素养要求学生不能靠单纯的刷题，而要去平心静气地感悟数学，理解数学，并能够应用数学.

【教育测量学依据】

新授课阶段容易忽视对教材中衍生内容(阅读部分等)的研究，重视概念、性质的解题应用；复习课阶段零散知识点容易遗漏；乃至实际形成学生的知识“盲点”，同时，重视章节所谓“重难点”教学，忽视概念的来龙去脉，导致学生对概念的一知半解.

【教学经验型依据】

易错点1：对教材阅读部分的圆锥曲线的光学性质，实际教学过程中很多教师会忽视，从而形成学生的知识盲点；

易错点2：学生容易借助不沿长轴方向的反射形成单一模式认知，形成D选项，忽视光线沿长轴方向的反射情况；

易错点3：意识到沿长轴方向的反射，但无法提炼出正确的运算形式导致结果出错.

2.命题意图

本题借助物理社团的光学实验发现椭圆的光学性质，注重对学生的劳动教育、实际动手能力的锻炼、发现问题、解决问题能力的培养；注重考查学生对椭圆基本性质、焦点三角形周长等的掌握，渗透分类讨论、化归与转化的数学思想，体现学生直观想象、数学运算、数学抽象学科核心素养，引导教师的教学要回归教材，要“接地气”，要重视对教材的研读、知识的拓展.

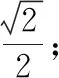
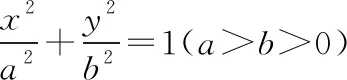
(1)求椭圆的方程；

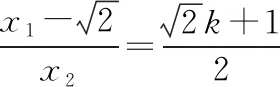
【试题解析】

(1)若选①.

若选②.

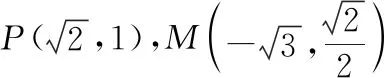
若选③.

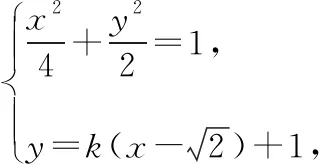
因为Δ≥0,

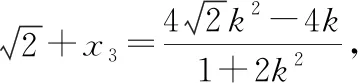
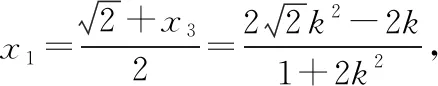
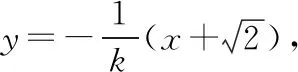
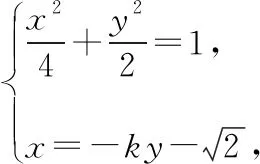
因为Δ>0,

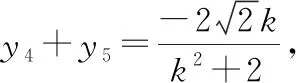
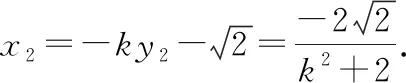
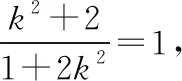
解得k=±1.

1.命题依据

【学科型专业依据】本题参照2020年新高考数学全国Ⅰ卷(供山东省使用)中的17题，命制为结构不良试题.圆锥曲线中直线与椭圆的位置关系是高考中的高频考点.

【教育测量学依据】本题难度系数为0.32，符合新高考20，21题的难度区间.

【教学经验型依据】

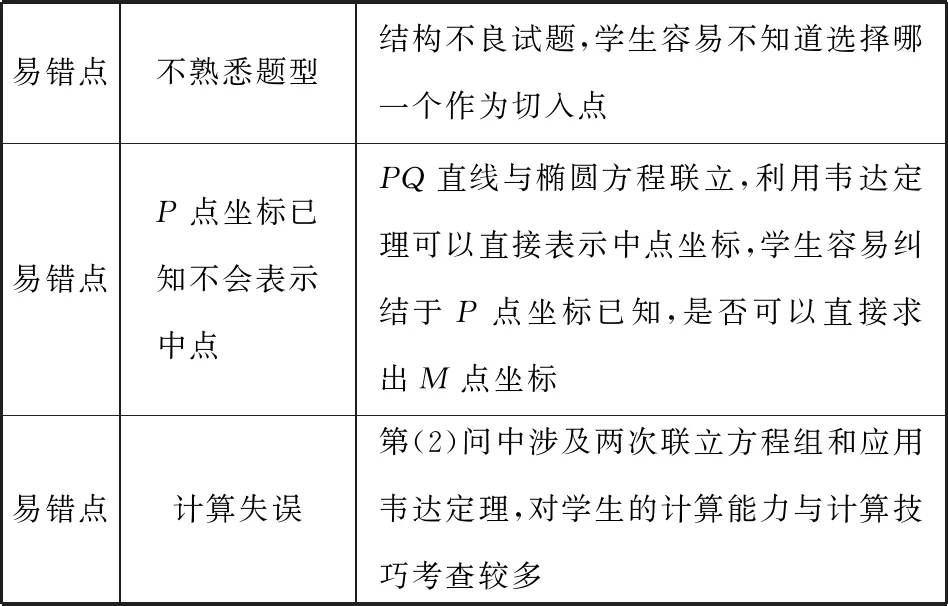
易错点不熟悉题型结构不良试题,学生容易不知道选择哪一个作为切入点易错点P点坐标已知不会表示中点 PQ直线与椭圆方程联立,利用韦达定理可以直接表示中点坐标,学生容易纠结于P点坐标已知,是否可以直接求出M点坐标易错点计算失误第(2)问中涉及两次联立方程组和应用韦达定理,对学生的计算能力与计算技巧考查较多

2.命题意图

本题基础性、应用性考查落实，以椭圆的相关知识点为背景，考查直线与椭圆的位置关系，考查学生的数学运算、逻辑推理的数学核心素养.