关于一维非线性晶格热传导的有限时间涨落定理

李金鸿，贺达海

（厦门大学 物理科学与技术学院，福建 厦门 361005）

1 研究背景

与平衡态的情况相比，非平衡统计力学缺乏统一的原理.因此，作为近年来非平衡统计物理的重要进展，涨落定理受到了大量关注.即使系统处于远离平衡态的情况下涨落定理也是成立的.任意时间窗口下熵产生的涨落关系首次在二维剪切流驱动的恒温流体粒子系统的数值模拟中发现[1]，并可基于混沌性假设给出证明[2].对于随机动力学涨落关系[3]，Kurchan[4]讨论了朗之万方程的情况，并且Lebowitz和Spohn[5]将此拓展到了广义马尔可夫过程.在这些早期工作中，涨落关系只在长时间极限下渐近成立，称之为传统SSFT,所考虑的物理量为环境中的熵产生（其等价于系统的热耗散），有着如下形式：

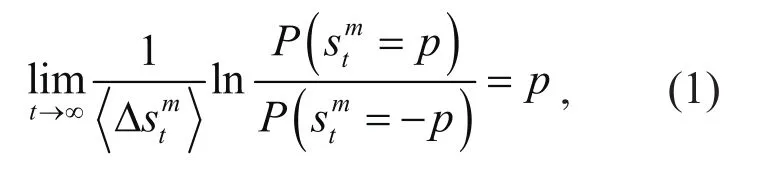
在前人的研究中，较少有人讨论在温度梯度驱动下的多体系统的SSFT.对于首末两端与不等温热库连接的一维链模型，简谐链热流的累积生成函数（CGF）满足特定的对称性[8]，事实上这种对称性在非线性链中也是满足的[9].根据大偏差定理[9]，如果CGF处处可导那么热流涨落的大偏差函数（LDF）可以经过CGF的勒让德变换得到，从而也可证明长时间极限下热流的涨落满足传统SSFT（1）.此外，与Nosé-Hoover热库耦合的FPUT-β模型的总热流的涨落符合传统的SSFT得到了数值验证[10].然而，还存在两个较少有人讨论的问题：（1）对于由温度梯度驱动的的多体相互作用系统，与Rt是否等价；（2）对于任意给定的温差和非线性，随着时间窗口的增加，的广义SSFT如何趋近于传统SSFT.本文研究了非平衡稳态下一维φ4链的主泛函、总熵产生与环境熵产生的涨落.首先，时间反演不具有对称性，从而与Rt不等价，使得在有限时间窗口下不满足涨落关系；对于任意给定的温差或非线性，随着时间窗口的增大，的广义 SSFT[7]均单调趋近于传统SSFT，而且对于一定的时间窗口，动力学过程不可逆性越强，广义SSFT与传统SSFT的差别越小.

2 理论分析

考虑一维非线性晶格，首末两端分别连接不同温度的郎之万热库.其动力学方程为：

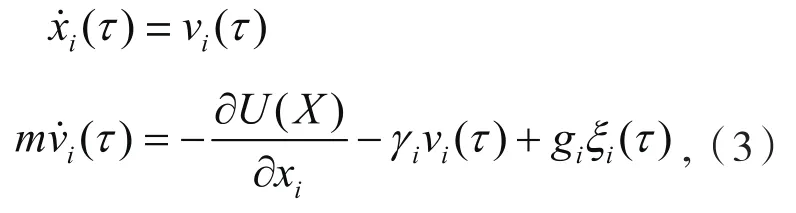
其中，所有粒子具有相同的质量m=1，它们与最近邻的粒子通过相互作用势进行耦合，且每个粒子上允许存在在位势，相互作用势与在位势均由势函数U(X)描述.x=(x1,x2,…,xN)和v=(v1,v2,…,vN)分别表示粒子偏离平衡位置的位移和粒子的速度（N表示系统尺寸或者粒子个数），则X=(x,v)表示系统在相空间中的状态.ξi(τ)是高斯白噪声，其满足〈ξi(τ)〉=0 和〈ξi(τ)ξi(τ')〉=2δ(τ-τ')，γi是的黏性系数 (γi=δi1+δiN)，噪声强度

接下来，我们考虑原始动力学的共轭动力学——时间反演动力学，其映射为：

任何时间窗口t下均符合稳态涨落关系的物理量是由共轭路径权重的对数比率给出的主泛函：

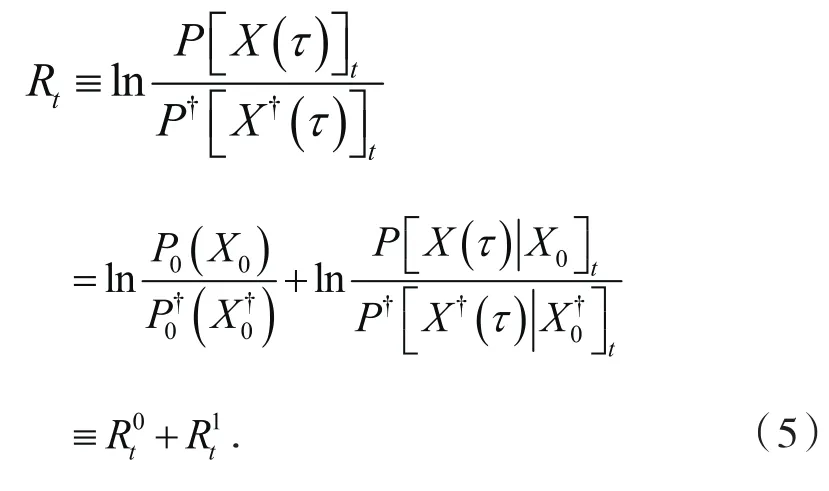
其由边界项和与过程相关的体项组成[6-7]，边界项为动力学轨道 [X(τ)]t和对应的时间反演轨道[X(τ)]t的两个初态的概率分布之比，方程（5）中P0表示系统的初始分布函数，且有P0=P1（P1表示系统的末态分布函数）.由Rt的定义（5）可知Rt[X(τ)]=-Rt[X(τ)]，即主泛函满足时间反演奇对称，那么根据广义涨落定理[7]可知，对于任意时间窗口，Rt应该满足如下涨落关系：

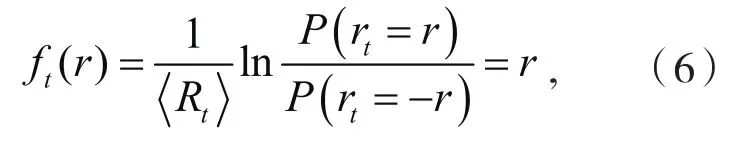
在郎之万方程路径积分表示中，体项能够容易地计算如下：

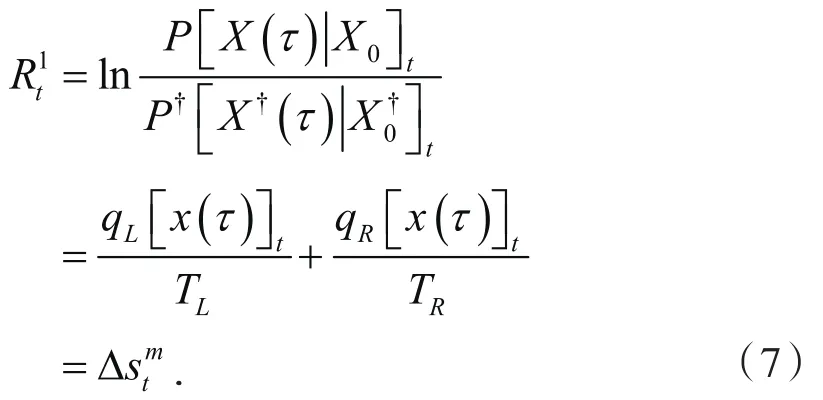
其中，qL、qR为系统热耗散，为环境熵产生，从而有

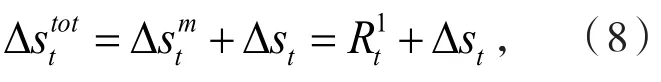
原始动力学对应的福克-普朗克方程为：

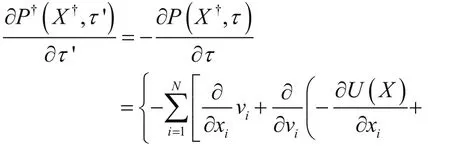
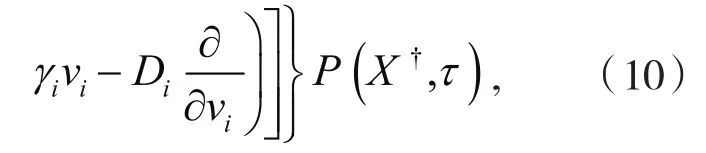
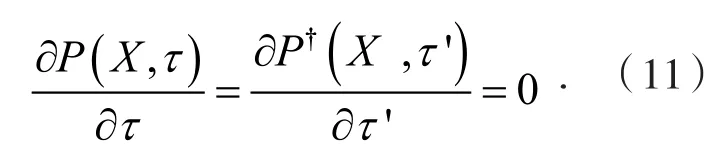
假设Ps(X)=Ps(X†)，由方程（9）（10）和（11）可知：

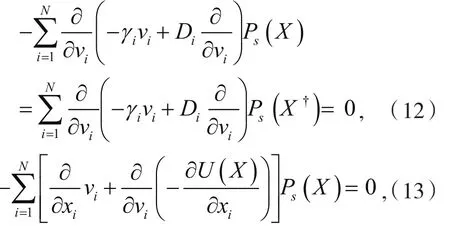
Ps(X)同时满足方程（12）和方程（13），但由于D1≠DN，方程（12）不具有关于v1和vN的置换对称性，说明除了平凡解（Ps(X)≡0）之外方程（12）的解Ps(X)不具有关于v1和vN的置换对称性，而方程（13）由于不含任何Di从而具有关于v1和vN的置换对称性，说明方程（13）的解Ps(X)具有关于v1和vN的置换对称性，前后互相矛盾说明系统的非平衡稳态分布不满足时间反演对称性（Ps(X)≠Ps(X†)）.因此对于由温度梯度驱动而处于非平衡稳态的一维非线性晶格，在有限时间窗口下ΔS ttot不满足时间反演奇对称性，同时也不满足涨落关系.我们的数值模拟结果证实了这点（见图1）.

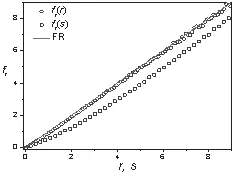
图1 关于rt或者的对数比率函数ft

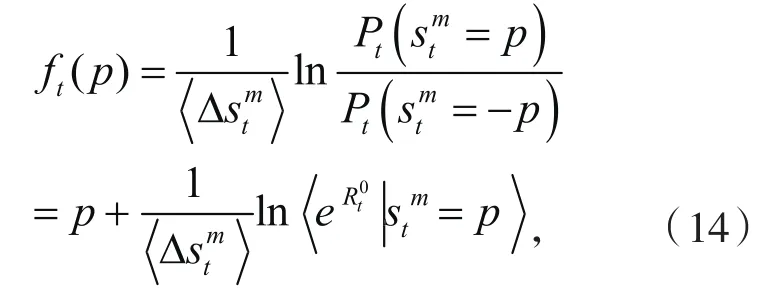
所以在有限时间窗口下ft(p)≠p，即不满足涨落关系，数值模拟的图2体现了这一点.根据大偏差定理[9-10]可知，在长时间极限下，应满足形如方程（1）的传统SSFT（或涨落关系），这与数值模拟给出的图2、图3和图4结果一致.

温差越大或者非线性越小，系统的热耗散速率越大（偏离平衡态的程度越大），这意味着动力学过程的不可逆性越强，关于的广义SSFT更快趋近于传统SSFT.

3 数值模拟

一维φ4链是非线性晶格的经典模型，本文将其作为物理模型进行数值模拟，证实了对于任意时间窗口，Rt满足涨落关系，而不满足.同时研究了的广义SSFT随着时间窗口的增加而趋近于传统SSFT的过程.

一维φ4链的运动方程（3）中的势能项U(X)应为：

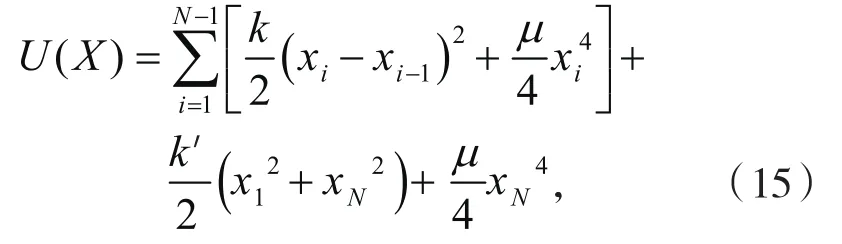
在以下计算中我们固定弹性系数k=1.并让k’=1以表示固定边界条件.

图2显示，对于任意给定的温差，有限时间窗口下的环境熵产生并不符合涨落关系，这与形如方程（14）的广义SSFT的预测一致.然而，当时间窗口逐渐增加时，环境熵产生的广义SSFT趋近于形如方程（1）的传统SSFT.

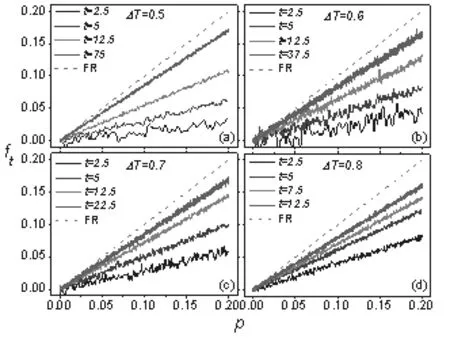
图2 不同相对温差下ft( p)对p的依赖关系图

为了描述的广义SSFT如何随着时间窗口增加而趋近于传统SSFT的过程，我们定义偏离函数（7）式给出了有限时间窗口t下广义SSFT与传统的SSFT的相对差别，其中pB表示环境熵取值的上限.从方程（1）可知

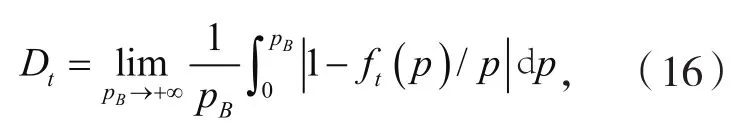
我们研究了不同温差和非线性对Dt的影响.由图3和图4可知，对于任意给定的温差或者非线性，的广义SSFT均随着t增加而单调趋近于传统SSFT，也意味着=0.此外，在一定的时间窗口下，温差越大或者非线性越小，平均环境熵产生速率

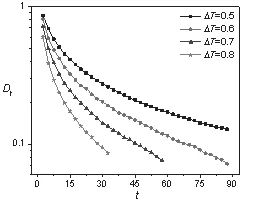
图3 不同相对温差下Dt对t的依赖关系图

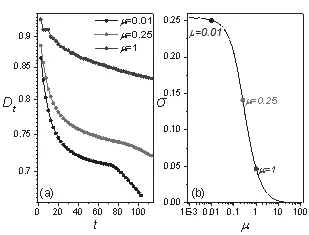
图4 非线性对Dt的变化行为的影响

越大（动力学过程的不可逆性越强），则Dt越小，亦即的广义SSFT与传统SSFT的差别越小，这与前文的理论分析结果一致.

4 总 结

本文研究了在温度梯度驱动下一维非线性晶格的主泛函、总熵产生与环境熵产生的涨落性质.首先，我们通过理论分析证实了系统的非平衡稳态分布时间反演不对称.这导致主泛函Rt与总熵产生不等价.我们进而用数值模拟验证了该理论分析，发现在有限时间窗口下一维φ4链的主泛函Rt符合涨落关系，而总熵产生并不符合.此外，通过数值模拟计算，我们发现对于任意给定的温差或者非线性，一维φ4链的环境熵产生的广义SSFT随时间窗口的增加均单调趋近于传统SSFT.结果表明动力学过程不可逆性越强，广义SSFT越快趋近于传统SSFT.