一类四次Hamilton函数Abel积分的零点个数估计

王彦杰，曹 勃，洪晓春

（1.宁波职业技术学院 数学教研室，浙江 宁波 315800；2.云南财经大学 统计与数学学院，云南 昆明 650221）

0 引 言

考虑扰动的Hamilton系统

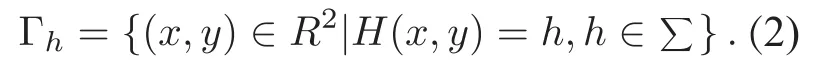
定义如下积分

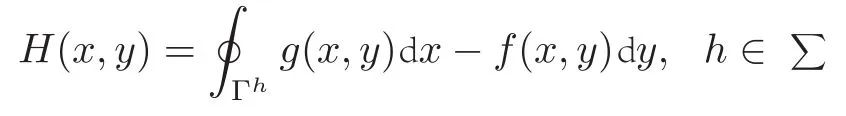
对于弱化的Hilbert16问题，Khovansky[2]和Varchenco[3]在1984年独立地证明了Z(m,n)的存在性，但都没给出Z(m,n)的具体表达形式[2-3].对于特殊形式的Hamilton系统H(x,y)=U(x)+V(y)，其中U(x)和V(y)分别是关于x和y的多项式，对此类Hamilton系统相关文献很多，例如，Petrov估计了H(x,y)=y2-x+x3,H(x,y)=y2+x2+x4和H(x,y)=y2-2x2+x4三类Hamilton系统相应的Abel积分零点个数[4-6].当时，其中degU(x)=4且使得(1)0至少有一个中心，赵育林和张芷芬证明了Z(m,n)≤7n+5[7]，对于四次Hamilton 系统H(x,y)=−x2+x4+y4和H(x,y)=x2+y2+ax4+y4，周鑫和李翠平得到了相应Abel积分零点个数的上界[8-9].对于Hamilton函数H(x,y)齐明辉和赵丽琴证明

对于Hamilton函数H(x,y)中含有xiyj时，这里i和j是正整数，目前研究结果很少，当m=2，未扰动系统含有周期环域时，其对应的Hamilton函数规范型可化为

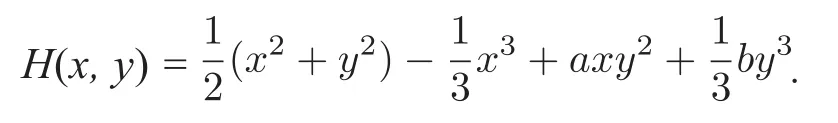
Horozov和Iliev应用Picard-Fuchs方程法证明了Z(m,n)≤5n+15[11].因此，针对原点是初等中心的Hamilton函数

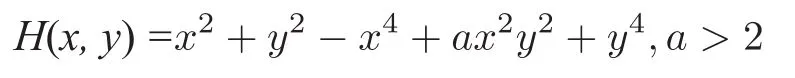
吴娟娟，张永康和李翠萍证明了Z(m,n)≤对于形如下面Hamilton函数

其中a≥0,a≠ 2，杨纪华和赵丽琴得到其Abel积分零点个数的上界[13].对于下面一类具有幂零中心四次的Hamilton系统

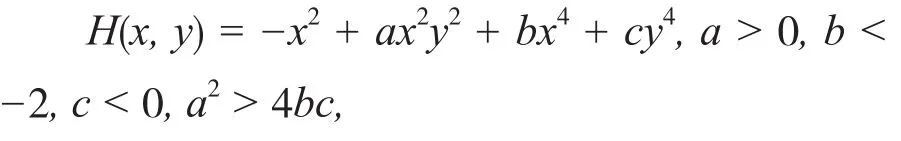
针对极限环问题，文献[15]研究具有m条切换线的扰动微分系统的极限环个数问题，文献[16]研究一类连续的分段线性Hamilton系统在一次多项式扰动下，周期闭轨族附近分支出极限环的个数问题.

受文献[7 − 17]的启发，本文研究如下的Hamilton系统.

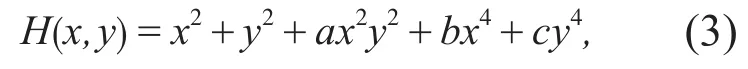
其中a2>4bc，a <2b，c <0，a <2c与之对应的向量场为

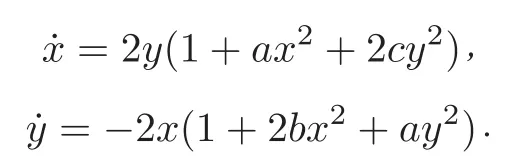
令

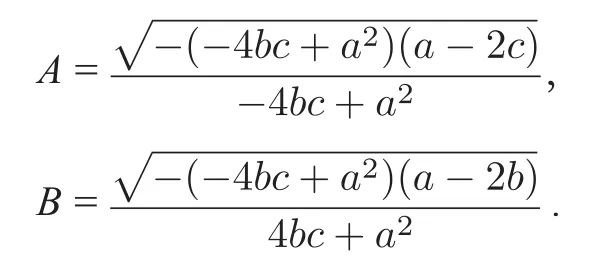
且该系统有一个幂零中点O(0,0)和四个鞍点Q1(A,B)，Q2(A,-B)，Q3(-A,B)和Q4(-A,-B).H(x,y)=0对应幂零中心对应于四个鞍点Qi(i=1,2,3,4)的多角环.且该系统只有一个围绕幂零中心O的有界周期环域，记其为且

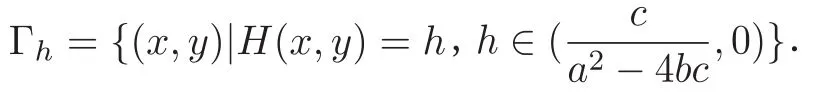
Z(n)为 Abel积分I(h)在上的零点个数(包括计重数)，

1 I(h)的代数结构

当h∈其中i和j是 自然数，由于Γh是关于坐标轴对称，因此Ii,2j(h)=0，I2i+1,2j+1(h)=0，所以我们只需考虑I2i,2j+1(h)=0即可.

引理1假设

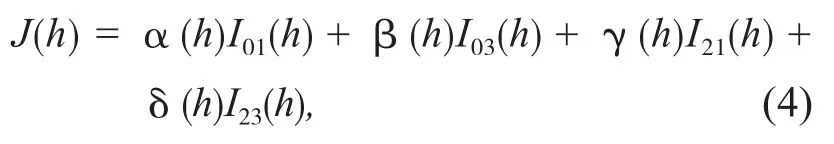
其中α(h)，β(h)，γ(h)和δ(h)是关于h的多项式，

证明根据Green公式可得

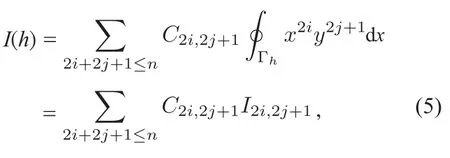
这里的C2i,2j+1是常数.

同时在(2)式两端对x求导可得

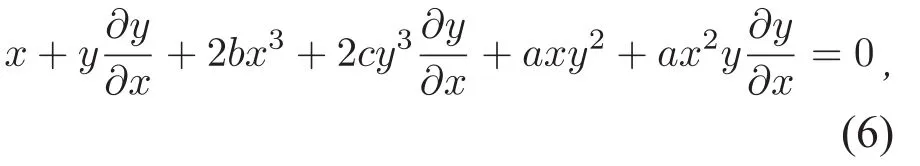
在(6)式两端同时乘以x2i一3y2j+1dx，然后沿Γh积分可得

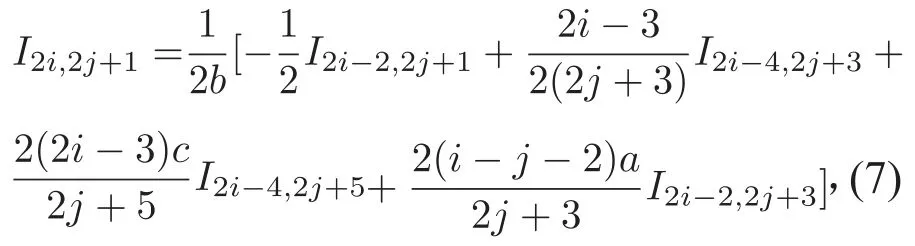
同样，在(3)式两端同时乘以x2iy2j一3dx，然后沿Γh积分可得

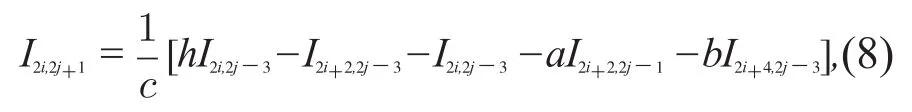
根据(7)和(8)可得

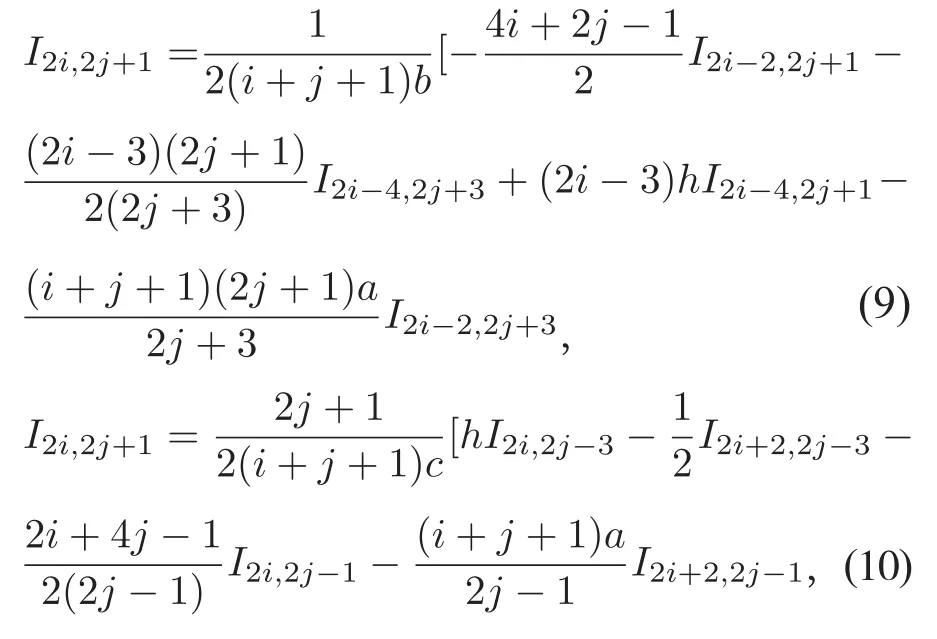
取i=2，j=0和i=0，j=2分别代入(9)式和(10)式，得到下面的等式

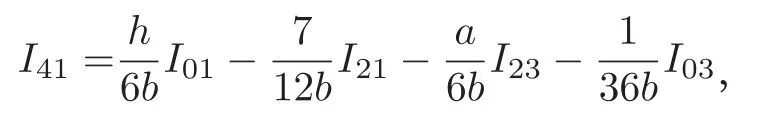
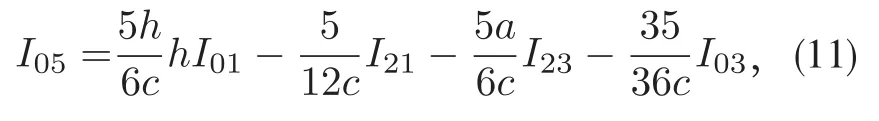
当n=5时，(4)式成立.设当2i+2j+1≤2k−1(k≥3)时，(4)式成立，则当(i,j)=(0,k),(1,k− 1),(2,k−2),…,(k− 2,2)和 (i,j)=(k− 1,1),(k,0)时，可推得

这里的A为

A是一个(k+1)× (k+1)阶矩阵，通过直接计算可得因此

这里的α2k-s，β2k-s，γ2k-s，δ2k-s，其中s=1,3 都是关于h的多项式，其中满足

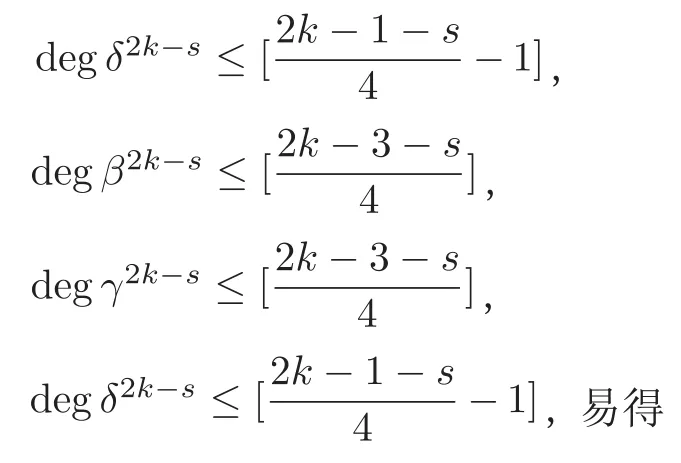
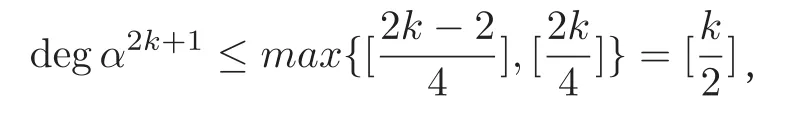
同理可得

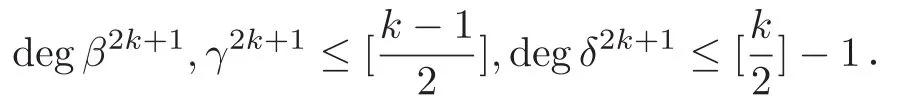
由以上证明可得，引理1成立.

2 Picard-Fuchs方程和Riccati方程

引理2记V=(I0,1,I0,3,I2,1,I2,3)T，这V满足下面的Picard-Fuchs方程

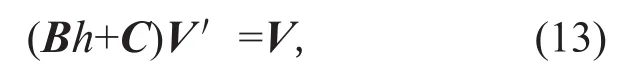
其中

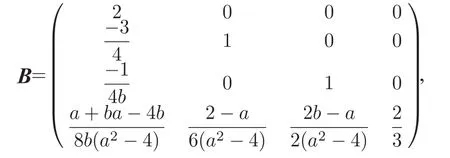
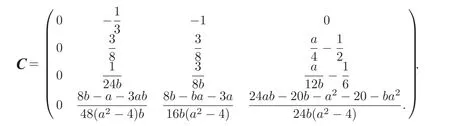
证明由(2)式可得

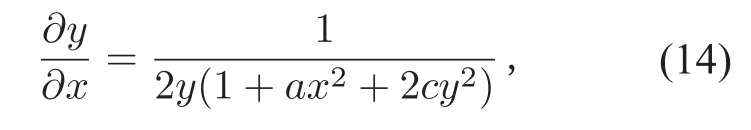
所以

因此

(15)式两端同时乘以h可得

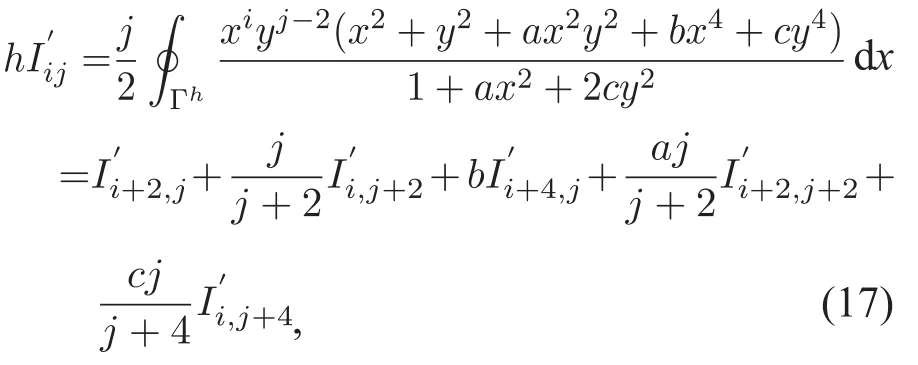
另一方面

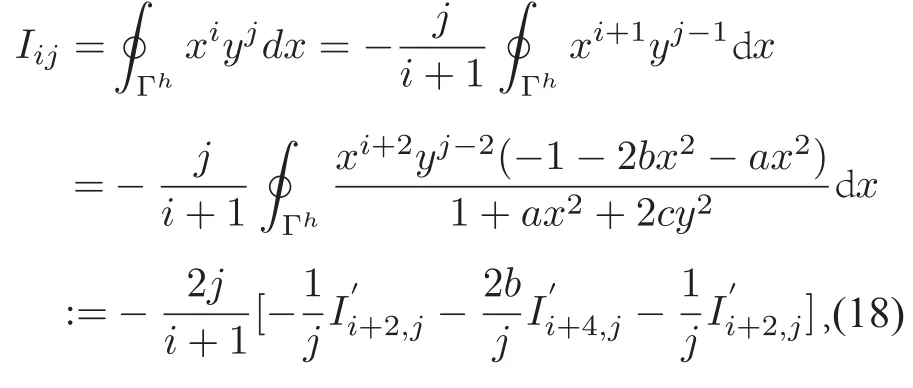
由(16)~(18)我们可以得到

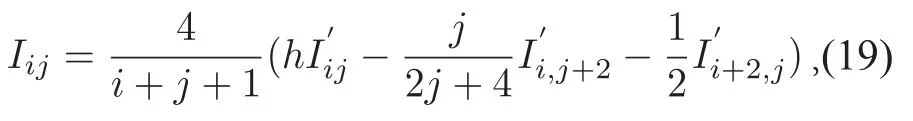
由(19)式可得

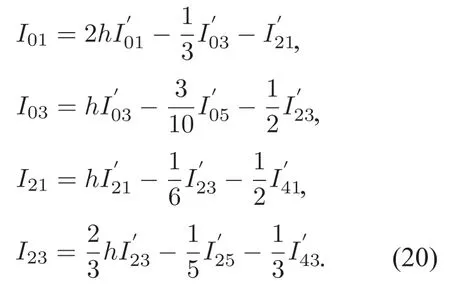
同时由(9)式和(10)式，即可推出引理2的结论成立.

取

我们可得如下引理

引理 3I01，I03，I21，I23和Z满足

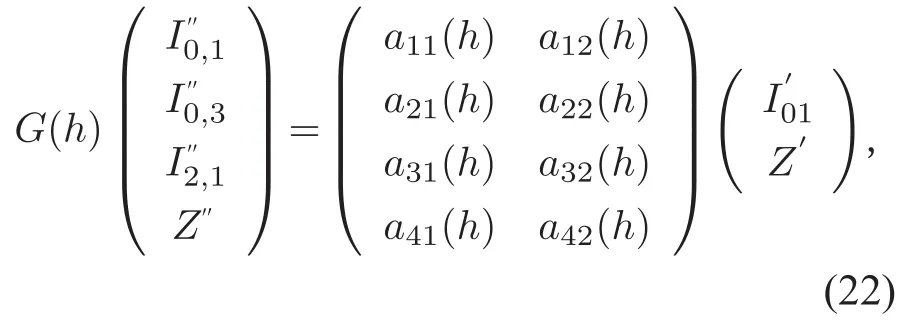
其中

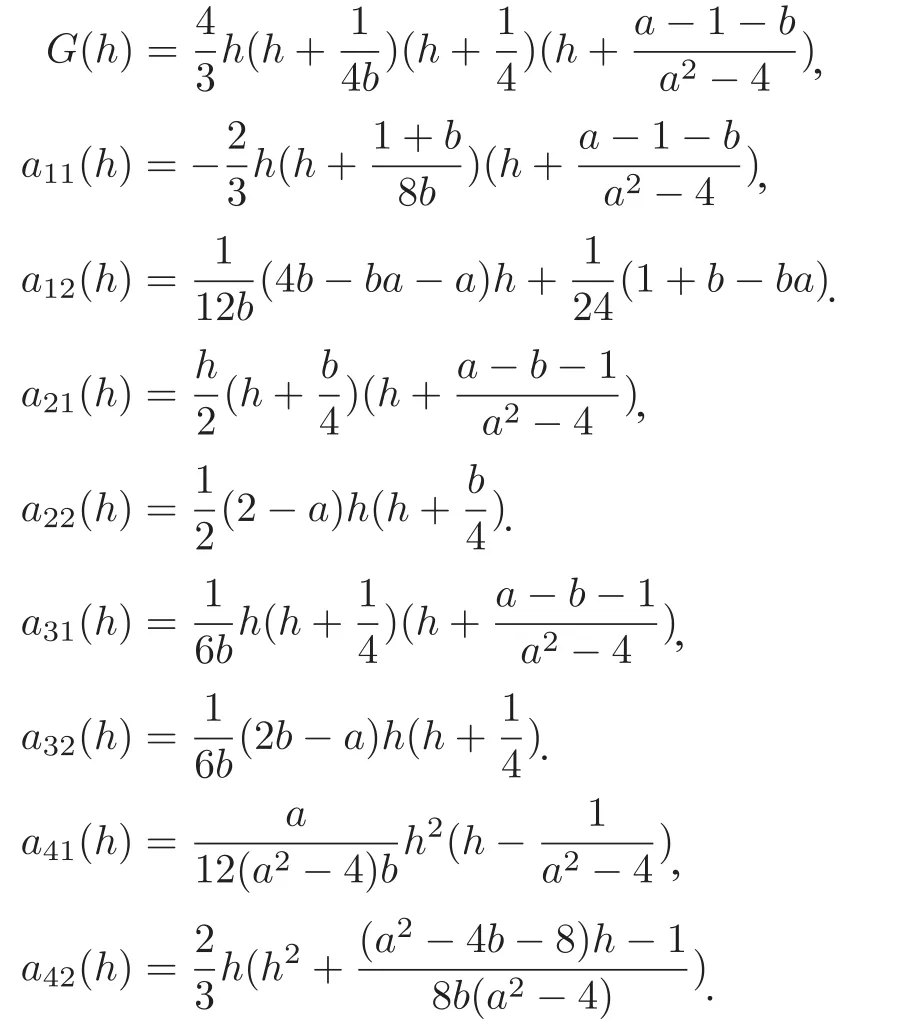
对(13)式两端的h求导得

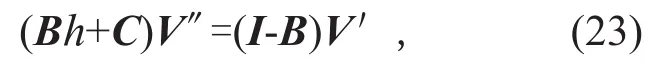
这里的I是4×4阶单位矩阵，然后把(21)式代入(23)式即可得到(22)式成立.

易知h∈∑时，所以可得如下引理:

引理4当h∈∑时，令则满足如下Riccati方程

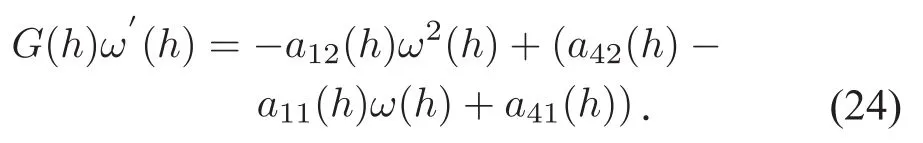
证明由(20)式中第一个和第四个方程既可得(24)成立.

3 主要结果和证明

由(4),(13)和(21)式得

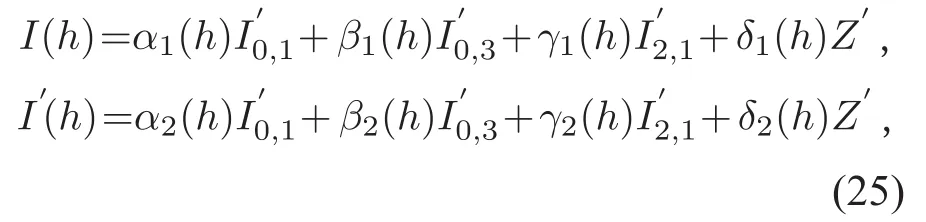
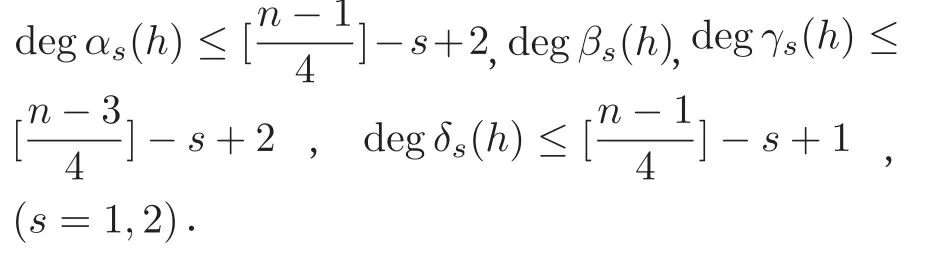
在 (25)式中消去I´2,1可得

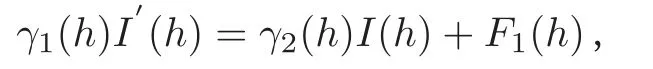
其中

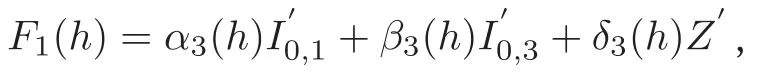
且

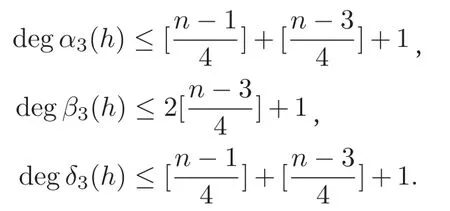
引理5[15]

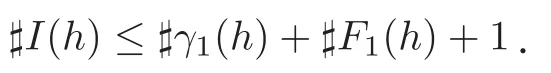
引理6设S是β3(h)和G(h)在 上的零点成的集合，则在上

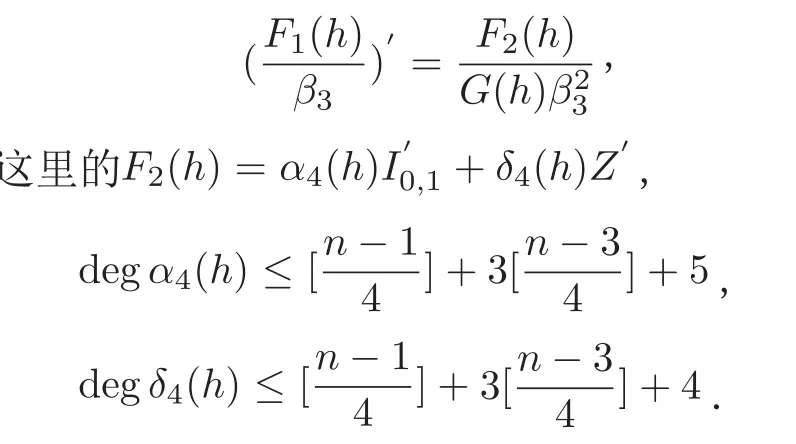
证明根据(20)式和F1(h)的定义可知，在上

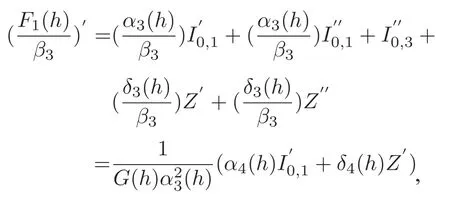
其中