基于深度学习的“3+1”数学解题教学策略

刘 俊,窦学芳,刘春燕,顾来芬,王丽萍,徐 晔,罗红英,杨静梅

（1.曲靖师范学院 应用数学研究所，云南 曲靖 655011；2.麒麟区第四中学，云南 曲靖 655011；3.麒麟区第七中学，云南 曲靖 655011； 4.马龙区第三中学，云南 曲靖655100；5.曲靖师范学院 数学与统计学院，云南 曲靖 655011)

0 引 言

为了落实“立德树人”的根本任务，当今研究最热的卓有成效的“深度学习”正是有力推进发展学生核心素养和基础教育课堂教学改革的重要实践途径.[1]为此，本文开展在深度学习引导下的“3+1”（理解、思考、探究+拓展）数学解题教学策略研究.通过改进数学解题教学，指导学生进行深度学习，不仅促进了学生的深度思考，而且培养了学生的数学核心素养，有力地推动了数学课堂的教学变革.本文提出的“3+1”数学解题教学,将课堂原来的以“教”为主改变为现在的以“学”为主，引导学生去发现问题，深度思考分析问题，运用所学知识去探究解决问题，对数学教学的本质更加关注，启发学生思维，提高课堂教学效率，让课堂以“学”为主的理念真正在深度学习的教学过程中得以落实.

1 “3+1”数学解题教学策略

本文提出的在深度学习引导下的“3+1”（理解、思考、探究+拓展）数学解题教学策略，就是为了克服和避免当前数学教学中存在的高耗低效问题、浅层学习问题和机械学习问题，教师对课标要求不熟导致教学目标笼统，对学科知识不厚导致教学内容含混，对教育理念方法掌握不够导致教学行为随意等问题.针砭时弊，目的是提高教师的教育教学理论水平，改变教师的课堂教学方式，改变学生的学习方式，培养学生自主学习能力，发展数学核心素养，促进学生深度学习数学.

深度学习引导下的“3+1”(理解、思考、探究+拓展)数学解题教学策略中，“理解”是指在设置的问题情景下去读懂题目，弄清题意，不仅仅是语言字面的意思，而是要分清楚未知量和已知量？有哪些条件？显性的条件是哪些？还要挖掘隐性的条件有哪些？本题的目的到底是要做什么？

“思考”是指寻找已知量与未知量之间的关系——直接或间接、显性或隐性？唤醒自己头脑中储存的相关知识，如何去建立数学模型或联想到类似的解题方法，根据学生自己的知识和经验背景,对新旧知识间的关系产生认知冲突，在反复的双向作用过程中主动建构起解题思路，对于学习数学而言，培养学生学会思考是很重要的.

“探究”是指在经过思考的基础上，对新问题重新认识，采用分析法、综合法、归纳法等数学思想方法，产生联想，以前是否做过此种相似题目，与该题有什么不同点？原来的解题方法是否还能适用？如果能适用，能运用到此题上吗？如果不适用了，又该如何改进方法呢？如果没有见过同种类型题目，那又该如何去寻找已知量与未知量之间的联系呢？探究解题的整个经历实际上就是一个探索知识发生、发展、演变和解决问题的过程，是培养学生数学思维和数学核心素养的过程.

“拓展”是指在回顾反思中向深度和广度两个方面拓展和提升.做完题后要养成总结反思的习惯，对所得的结果能否进行验证其正确性，一方面，此题还有不同的方法求解吗？拓展学生解题思路，开阔学生思维，这就是常说的“一题多解”.另一方面，提倡变式，在原型题的基础上进行变化，以不同的题目呈现，可以加大题目难度，也可以增加多个知识点在同一个题中，此时，还能用这种方法求解吗？如果不行，要在原解题方法的基础上作哪些改变？在做完这些题目后，要经过总结反思，会发现这一类题目实际上是源于同一种解题方法，这就是多题一解，是以一种解题方法为基准，去求解一类题目.

2 案例研究

为了能充分理解和运用深度学习引导下的“3+1”数学教学策略，我们选取中学数学教学中的案例之一来阐述.[2]以具体说明如何运用“3+1”数学教学策略的.

问题：从1～9这9个不同数字中组成两个2位数，每一个数字最多只能使用一次，怎么样组成才能使这两个数的乘积最大？

理解：是具体的数字，要组成两个2位数，注意到没有“0”，每一个数字最多只能使用一次，要达到这两个数的乘积最大.

思考：把所有符合要求的2位数全部找出来，然后依靠真正的具体数字运算来完成，就能找到最大数.

探究：采用穷举法，符合要求的两个2位数的乘积有个数，只需全部计算出来，再从中取最大数即可，这种方法虽然能达到目的，但计算量太大、太繁.那么，我们能否找到一个比较大小的一般规律（模型）？为了找到解题思路，我们有一个比较简单的公式也许能帮助理清解题思路，那就是

通过观察分析此公式，得到：

性质1：两个正数，当它们的和越大、差越小时，则这两个正数的乘积越大.

性质1其实就是两数的“算术—几何”平均值定理的推广，由此可知：若两数之和为定值时，则当此两数相等时，它们的乘积取最大值.

但问题是：无法直接运用性质1，那我们就从最简单的情形去寻找解题思路，当x、y均为1位数时，显然当x=9,y=8或x=8,y=9时，xy=72最大.但现在x、y均为2位数，为了使xy最大，x、y必定取1～9中的4个较大的数6～9，则有三种情形(x,y)=(98,76)，(x,y)=(97,86)，(x,y)=(96,87)，分别对应xy=7448,8342,8352.因此，当x=96，y=87时，xy=8352最大.

拓展1：能否有进一步的方法使我们在三个组合(x,y)=(98,76)，(x,y)=(97,86)，(x,y)=(96,87)中直接选(x,y)=(96,87)呢？我们有下面的性质2.

性质2：对两个2位数，十位数较大时在个位数选较小的，十位数较小时在个位数选较大的，则这两个2位数的乘积最大.

证明：不失一般性，设x1>x2>x3>x4，xi∈{1,2,3,4,5,6,7,8,9}，i=1,2,3,4，则两个2位数的乘积组合共有三种：

(10x1+x4)(10x2+x3)，(10x1+x3)(10x2+x4)，(10x1+x2)(10x3+x4).

可得

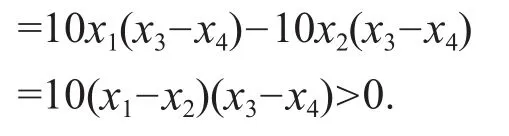
由于x1≥x2+1，x2≥x3+1，x3≥x4+1，x3≤9，x2x4＜ 100，有

因此，组合(10x1+x4)(10x2+x3)最大，性质2证毕.

根据性质2，立即可得出当x，y为2位数时，(x,y)=(96,87)最大.

拓展2：试用1～9这9个不同数字中取6个组成两个数，每个数字只能使用一次，怎样组成才能使这两个数的乘积最大？

从1～9这9个不同数字中取6个组成的两个数没有位数限制，会出现三种组合的乘积情况：3位数与3位数，4位数与2位数，5位数与1位数.若采用穷举法，符合要求的两个数的乘积有=30240+30240+30240=90720个数，显然穷举法的这种解题思路是行不通的.现在需要确定：3位数与3位数的乘积最大，还是4位数与2位数的乘积最大，还是5位数与1位数的乘积最大？我们得到下面的性质3：

性质3：从1～9这9个不同数字中取6个组成两个数，每个数字只能使用一次，则两个3位数的乘积最大.

证明：设a1，a2，a3，a4，b1，b2是从 1～9 中不同数字中取出的6个数字，组成的两个数字的乘积有三种情况：3位数与3位数，4位数与2位数，5位数与1位数.不失一般性，假设a1a2a3a4为4位数，b1b2为2位数，其中ai，bj∈{1,2,3,4,5,6,7,8,9}，i=1,2,3,4，j=1,2，则有

即3位数与3位数的乘积>4位数与2位数的乘积.

即3位数与3位数的乘积>5位数与1位数的乘积.故3位数与3位数的乘积最大，性质3证毕.

综合性质1、性质2、性质3，可知：当x，y取自1～9这9个不同数字中的6个数时，组合(x，y)=(964,875)使xy最大.

拓展3：试用1～9这9个不同数字中取8个组成两个数，每个数字只能使用一次，怎样组成才能使这两个数的乘积最大？

若采用穷举法，两个数字的乘积有四种情况：4位数与4位数，5位数与3位数，6位数与2位数，7位数与1位数.符合要求的两个数的乘积有725760个数，显然穷举法这种解题思路是行不通的.

但我们根据性质1、性质2、性质3，当x,y取自1～9这9个不同数字中的8个数时，组合(x，y)=(9642，8753)使xy最大.事实上，我们有：

性质4：从1～9这9个不同数字中取8个组成两个数，每个数字只能用一次，则两个4位数的乘积最大.

证明：设a1，a2，a3，a4，b1，b2，b3，b4是从 1～9中不同数字中取出的8个数字，组成的两个数字的乘积有四种情况：4位数与4位数，5位数与3位数，6位数与2位数，7位数与1位数.不失一般性，假设a1a2a3a4为4位数，b1b2b3b4为 4 位 数， 其 中ai，bj∈{1,2,3,4,5,6,7,8,9}，i=1,2,3,4，i=1,2,3,4，则有

即4位数与4位数的乘积>5位数与3位数的乘积.

即4位数与4位数的乘积>6位数与2位数的乘积.

即4位数与4位数的乘积>7位数与2位数的乘积.故两个4位数的乘积最大，性质4证毕.

拓展4：试用1～9这9个不同数字组成两个数，9个数字都用完，且每个数字只用一次，怎样组成才能使这两个数的乘积最大？

根据性质1～4，只有两种选组合(x,y)=(96421,8753)与(x,y)=(9642,87531)，只能在这两种情况中产生乘积最大，因此，只须比较96421×8753与9642×87531的大小.

96421×8753=843973013，9642×87531=843973902.

则当(x,y)=(9642,87531)时，xy=843973902为最大.

拓展5：能否找到判定96421×8753与9642×87531大小的一般性方法.

性质 5：若a>b>0，c>0，则a(10b+c)>b(10a+c).

证明：由于a>b>0，c>0，则

a(10b+c)-b(10a+c)=ac-bc=c(a-b)>0.

性质5证毕.

根据性质 5，取a=9642，b=8753，c=1，则a>b，

a(10b+c)=9642×(10×8753+1)=9642×87531，

b(10a+c)=8753×(10×9642+1)=8753×96421.

因此，由a(10b+c)>b(10a+c)知：9642×87531>8753×96421.

本案例如果没有前面的辅垫而直接解答拓展4，题目难度明显太大，学生将无从下手去做.从直觉上，用穷举法算出所有可能的乘积，就可以得到最大数，但这种解题思路明显是行不通的，组合情况太多，运算量太大了.但经过我们的“3+1”教学设计，用与学生认知相称的问题作铺垫，以激起学生的好奇心和求知欲，这样，用一些具有挑战性的、激励性的问题去引导学生深度思考和进行探究，遵循“理解→思考→探究→拓展”的思路解决问题，由简单到复杂，由易到难，方法由特殊到一般，又由一般回归特殊，引导学生进行深度学习，思维层次由具体到抽象、由低级到高级，逐步推进问题的深化，逐级化解难度，使拓展4的问题就容易求解了.这种基于深度学习的“3+1”数学解题教学方法培养了学生发现问题、分析问题和解决问题的能力，发展了学生的数学核心素养，[3]促进学生数学素养的提高.

3 总 结

本文在深度学习引导下提出的“3+1”(理解、思考、探究+拓展)数学解题教学策略，是对波利亚提出的怎样解题四步曲“理解题目、拟定方案、执行方案、回顾”的提炼和升华，[4]是对《全日制义务教育数学课程标准》第三学段（7～9年级）提出的“本学段的教学内容采用“问题情景—建立模型—解释、应用与拓展”的模式展开，让学生经历知识的形成与应用的过程，从而更好地理解数学知识的意义，掌握必要的基础知识与基本技能，发展应用数学知识的意义与能力，增强学好数学的愿望和信心.”的具体实施策略.[5]“3+1”数学解题教学策略经多所中小学校实践取得了明显效果，提高了学生发现问题、分析问题和解决问题的能力与水平，增强了学生学习数学的自信心，培养了学生的数学核心素养，[6]提高了教学质量.

本文对深度学习引导下的“3+1”数学解题教学策略进行了探索与实践，在教学过程中，突出了以“学生”为主体，以学生的“学”为主，学生运用所学知识去探索问题的求解，引导学生深度学习，从中获得解决问题的经验与策略，以掌握数学的学习方法和养成良好的思维方式.教学过程从简单到复杂，知识由浅入深，逐步引导学生去探索问题，难度逐步增大，整个过程体现了学生的认知规律，并能将具体问题抽象为一般问题，形成规律（性质），这正是“发现→猜想→论证”的数学思维过程.