∑1-SDD矩阵线性互补问题的最优误差界
李艳艳
(文山学院 数学学院,云南 文山 663099)
0 引 言
线性互补问题(Lcp(A,q))的模型是指求x∈ Rn,满足

其中A是实矩阵,x,q是实向量.
文献[1]指出,当Lcp(A,q)中的矩阵A是主子式都为正的实矩阵(P矩阵)时,能较容易得到该问题唯一解的误差界.
2006年,陈小军等在文献[2]中给出了Lcp(A,q)中的矩阵A是主子式都为正的实矩阵(P矩阵)时的线性互补的误差界

其中r(x)=min{x,Ax+q}, ,d=[d1,d2,…,dn]T(0≤di≤1).
本文研究目前少有文献研究的H矩阵的新子类∑1-SDD矩阵的线性互补问题的误差界估计.首先给出∑1-SDD矩阵A的逆矩阵无穷范数的上界.其次,利用严格对角占优矩阵经典的线性互补误差界估计式,得到了∑1-SDD矩阵A的线性互补问题的误差界,进一步对该误差界的最优值进行了详细地分析.同时借助数值算例对估计式的优越性进行了说明.
1 预备知识

Pena在文献[9]中首次给出了H矩阵的新子类∑1-SDD矩阵,定义如下:
定义1[9]对于矩阵A=(aij)∈Rn,n,如果存在非空子集S⊆N,使得:
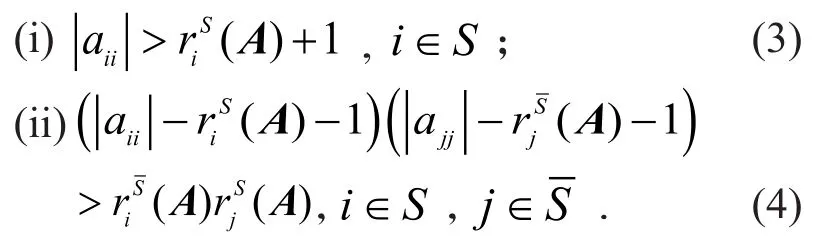
成立,则称A是∑1-SDD矩阵.
引理1[9]设A是主对角元素为正的∑1-SDD矩阵,X满足定义1.则存在对角矩阵且

对i∈N和γ∈Is,有

引理2[9]设矩阵A严格对角占优,则

2 ∑1-SDD矩阵无穷范数的上界估计
本部分利用构造的方法,给出∑1-SDD矩阵仅与矩阵元素有关的无穷范数的上界.
定理1设矩阵A=(aij)∈Rn,n是∑1-SDD矩阵,则

下面分类讨论:

接下来,研究∑1-SDD矩阵A的最小奇异值的下界.利用1-范数和∞-范数的关系,易得定理2,定理3.
定理2设矩阵,则
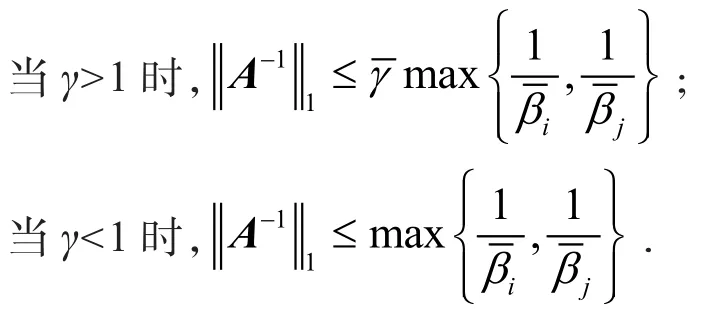
定理3设A=(aij)∈Rn,n,AT和A是∑1-SDD矩阵,则
当γ>1时,

当γ<1时,

3 ∑1-SDD矩阵线性互补问题的误差界
本部分研究∑1-SDD矩阵线性互补问题的误差界,同时对最优值进行详细地分析.
引理3[9]设A=(aij)∈Rn,n是对角元素为正的对角矩阵,且AX是严格对角占优矩阵,设

定理4设矩阵A=(aij)∈Rn,n是∑1-SDD矩阵,S⊆N,S≠∅,aii>0,令则对∀i,j∈N,有

证明直接应用引理便得结果.
下面分γ>1和γ<1讨论误差界的最优值.当γ>1时, 令若存在,则
定 理 5设 矩 阵A=(aij)∈Rn,n是 ∑1-SDD矩阵,S⊆N,S≠∅,aii>0,令=ID+DA=(),D=diag(di),0≤di≤1,γ>1,


定理6设矩阵A=(aij)∈Rn,n是∑1-SDD矩阵,S⊆N,S≠∅,aii>0,令=I-D+DA=(),D=diag(di),0≤di≤1,γ<1,,则

证明(1)若,且γ

因为g′(γ)< 0,则g(γ)在区间上为单调递减函数,于是

证毕.
4 数值算例
例1设,经验证当S={1}时,A1为∑1-SDD矩阵,且,应用定理5计算得
例2设经验证当S={1,2}时,A2为∑1-SDD矩阵,且应用定理5计算得
本文的研究将线性互补问题误差界研究的矩阵进行了扩充,填补了对于∑1-SDD矩阵该类问题研究的空白.得到的结果,不仅形式简单,且由于只与矩阵元素有关,易于计算.与已有关于线性互补误差界问题研究方法相比,定理5、定理6在定理4的基础上,利用函数的单调性讨论确定了含参数误差界的最优值.这也是对该类问题研究方法的进一步拓展和丰富.

