基于势能守恒的微低重力模拟系统

安小康， 牛博， 王兆魁， 危清清， 陈力

(1. 福州大学机械工程及自动化学院， 福建 福州 350108； 2. 清华大学航天航空学院， 北京 100084；3. 中国空间技术研究院北京空间飞行器总体设计部, 北京 100094)

0 引言

随着我国载人航天工程的不断发展和空间任务的不断涌现， 航天任务验证和航天员在地训练需求增大[1-4]. 在医疗领域， 低重力模拟技术可用于步行障碍患者的神经康复辅助训练和物理治疗及航天医学研究[5-8]， 因此， 研发多自由度、 低成本、 使用简单、 操作灵活的微重力模拟设备具有重要意义.

目前， 空间微重力环境地面模拟主要有落塔法[9-10]、 抛物线飞行[11-12]、 中性浮力水池[13-14]、 悬吊式重力补偿系统[15]、 气悬浮法[16-17]、 被动式外骨骼系统[18-20]、 虚拟现实技术[21-22]等. 落塔法能精确模拟空间微重力环境且可以进行三维空间的微重力实验， 但其制造成本高， 通用性差， 单次微重力模拟时间短； 抛物线飞行微重力模拟相比较于落塔法， 其模拟时间有所增加， 但成本仍然很高， 安全性较差； 中性浮力水池微重力模拟克服了时间、 空间的限制， 但制造、 维护成本极高， 对训练设备的密封性有严格要求， 且水的动态阻尼和粘滞效应会降低模拟精度[23]； 悬吊式重力补偿系统结构复杂， 悬吊绳必须经过被悬吊体质心， 但在实验过程中随着被悬吊体质心不断移动, 被悬吊体很难在三维旋转方向保持平衡， 此外悬吊式重力补偿对训练对象的自由度影响也较大； 气悬浮法相比较其他方法制造成本和维护成本较低， 但气悬浮法只能在平面上对被失重物体的重力进行补偿， 其运动自由度受到限制； 被动式外骨骼系统只能对物体局部进行重力补偿； 虚拟现实技术则无法提供低重力体感. 针对以上问题， 本研究研发一种低成本、 多自由的基于势能守恒的被动式低重力模拟系统.

研究首先基于Lagrange第二类方程， 推导出系统的动力学方程， 然后对系统的静力学、 动力学特性进行仿真分析. 对于低重力模拟系统模拟月面低重力环境工况， 仿真分析航天员在该模拟环境中跳跃时的动力学特性. 针对动态补偿不是很理想的问题， 提出摩擦补偿和惯性补偿思路.

1 系统原理

1.1 系统组成

如系统结构图(见图1)所示， 微低重力模拟系统由结构本体、 弹簧系统、 旋转台、 平行四边形系统、 升降系统、 人机接口系统等组成. 升降台及两平行四边形实现航天员的前后、 上下两个自由度方向的移动， 旋转台实现航天员的左右摆动. 航天员训练过程中， 机构重力势能及航天员重力势能与弹簧系统弹性势能间相互转换并保持总能量守恒， 实现任意位置的失重模拟. 该系统结构简单、 制造成本低、 可实现0～1g任意重力环境的模拟.

图1 系统总体结构图Fig.1 System structure diagram

1.2 重力补偿原理

微低重力模拟装置运动学参数如图2所示， 图中两个平行四边形机构处的弹簧刚度分别为k1、k2， 杆长分别为l1、l2， 杆质量分别为m1、m2， 杆质心与杆转动关节点距离分别为r1、r2， 杆与坐标系XOY的Y轴正方向夹角分别为θ1、θ2， 第一个平行四边形连杆转动中心高度为h1， 上下连杆距离为h2， 两弹簧上端连接点距两平行四边形上连杆转动中心分别为d1、d2， 第一、 第二平行四边形中间连接件质心在A2、A3中点位置， 其质量为m3， 人机接口质量为m4， 航天员质量为mb， 人机接口与航天员总质心与第二个平行四边形下连杆末端水平距离为r3， 竖直方向在上下两连杆末端点连线中垂线上.系统机构的总势能由重力势能和弹簧的弹性势能组成， 根据被动静平衡原则， 系统工作空间内任何工作构型下的总势能恒定.数学上表述为

图2 躯干被动重力补偿机构运动学参数Fig.2 Kinematic parameters of trunk passive gravity compensation mechanism

VTotal=VMG+VBG+VS=Constant

(1)

式中:VMG，VBG和VS分别代表系统机构、 人体和弹簧的总势能. 式(1)成立的条件是假设人体的重力全部得到补偿. 如果只是部分重力需要得到补偿， 则式(1)应改为

VMG+ρVBG+VS=Constant

(2)

式中: 因子ρ是被补偿的人体重力与人体所受重力的比值.ρ只是与人体势能有关的因子， 因为机构需要按期望比例补偿人体重力， 而机构自身重力在任何时候都需要百分之百被补偿， 这样受训者将不需要承受机构的重力.

根据图2中所定义的运动学符号， 整个系统的总势能可以用关节转角表示如下:

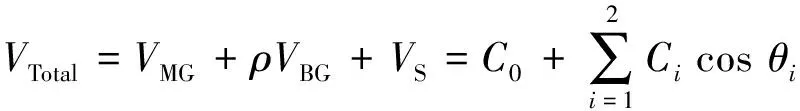
(3)

其中，

式(3)中， 为保证系统在任何构型总能量恒定， 必须使式(3)等式右边第二项恒为零， 即平衡的条件为

Ci=0 (i=1, 2,…)

(5)

此时， 由式(5)及已知的机构和人体质量及几何参数, 可计算出一组弹簧刚度值k1、k2如下:

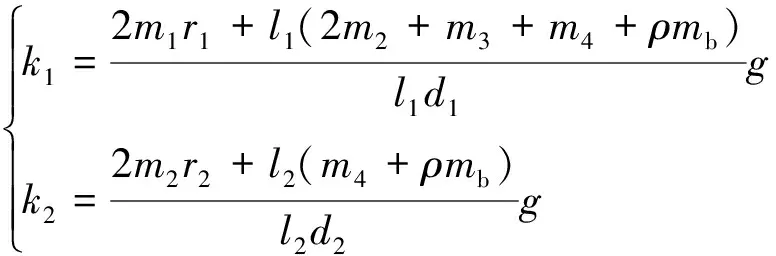
(6)

当失重装置和人体动力学参数确定后， 根据(6)式选择对应刚度的弹簧， 可使得总势能独立于构型变量θ1、θ2， 即在任意构型下均能满足总势能守恒. 若需要模拟不同的失重条件(如将ρ设置为1， 即实现100%人体重力补偿； 模拟月球活动需要设置ρ为0.83， 而模拟火星活动需要设置ρ为0.62)， 只需将对应的补偿因子ρ带入(6)式计算出相应弹簧刚度即可.系统设计中， 考虑到需要切换不同的重力模拟环境或航天员体质量有所变化， 将系统中弹簧的上端位置设计为可调, 即d1、d2可调， 当变化较小时， 由(6)式知， 可调整d1、d2达到相应目的， 当变化较大时， 可直接更换较大刚度的弹簧来实现.

2 系统建模

2.1 运动学建模

微低重力模拟系统运动学参数如图2所示， 设广义坐标为θ=[θ1,θ2]T， 航天员质心与人机接口质心位置在同一水平线上， 航天员质心位置P(xp,yp)可表示为

(7)

等式两边对时间求导并整理得

(8)

(9)

2.2 动力学建模

与运动学建模类似， 设广义坐标为θ=[θ1,θ2]T， 第一、 第二平行四边形连杆转动惯量分别为I1、I2， 弹簧刚度矩阵为k=[k1,k2]T， 其他动力学参数如图2， 不考虑弹簧自重， 则由Lagrange第二类方程， 可推导出系统的动力学方程为

(10)

(11)

式中

从动力学模型可知， 重力补偿比例由ρ决定.当ρ=1时，G(θ)=0， 无外力作用时，F=0， 其中0=[0, 0]T, 系统动力学模型变为

(12)

此时， 系统为典型完全失重系统， 人体重力和机构重力被完全补偿.

3 仿真分析

为验证微低重力模拟系统的动力学、 静力学特性， 设计两组仿真实验， 分别是： 航天员经该系统重力补偿后地面对其支撑力实验； 航天员经该系统重力补偿后自由落体实验. 仿真时， 设置系统惯性参数，m1=m2=6 kg，m3=16 kg，m4=18 kg，mb=90 kg，l1=l2=1 m，r1=r2=0.5 m，r3=0.4 m，I1=I2=0.5 kg·m2，h1=1.68 m，h2=0.45 m，d1=0.6 m，d2=0.4 m，g=9.8 m·s-2，f=5 N·m.

3.1 静力学特性仿真实验

为验证该系统模拟不同重力环境时系统对航天员的重力卸载性能， 仿真验证系统在模拟不同重力环境时， 挂载在末端的航天员站立在地面时地面对航天员的支撑力. 仿真中， 模拟的重力环境为0～1g， 即ρ∈[0, 1]. 不考虑关节静摩擦， 由系统动力学模型可知， 当航天员站立在地面并受力平衡时， 根据力平衡原理， 环境对整个系统的输入外力即为失重模拟系统未补偿的重力， 通过动力学模型计算得到的末端受力F就是航天员受到的地面支撑外力， 对比实验为航天员在该重力环境中站立时地面对其的理论支撑力， 结果如图3所示. 由图3可以看出， 在不同的重力补偿水平下， 地面支撑力的仿真结果与理论计算结果符合得非常好， 证明了该装置静力学补偿的有效性.

图3 不同重力补偿条件下航天员所受地面的支撑力 Fig.3 Supporting force of the ground under different gravity compensation conditions

3.2 动力学特性仿真实验

为验证重力补偿系统对航天员动力学特性的影响， 仿真在0.5g(ρ=0.5)重力补偿水平下, 经该装置重力补偿后航天员的自由落体运动过程, 包括航天员质心位置曲线和质心速度曲线.对比实验为航天员在0.5g重力环境中自由落体时理论的运动过程.

仿真实验结果如图4所示， 图4(a)、 (b)是经重力补偿装置补偿后及理论计算的航天员在竖直方向的位置和速度曲线， 仿真结果与理论结果具有相同的趋势， 但仿真结果与理论结果在竖直方向存在0.2 m的位置误差和1 m·s-1的速度误差； 图4(c)、 (d)为水平方向的位置和速度曲线， 理论位置和速度均保持不变， 但仿真结果中位置曲线与速度曲线有所变化， 位置误差为0.05 m， 最大速度误差为0.13 m·s-1. 分析其原因为： 理论计算仅采用宇航员的自由落体模型， 无其他附加质量， 但在实际的微低重力模拟装置中， 各运动构件存在质量， 关节存在摩擦力， 故航天员在该重力补偿装置作用下自由落体时， 航天员与设备间存在动力学与运动学耦合， 航天员的动力学特性会受到低重力模拟系统的运动构件附加惯性和关节摩擦力矩的影响.

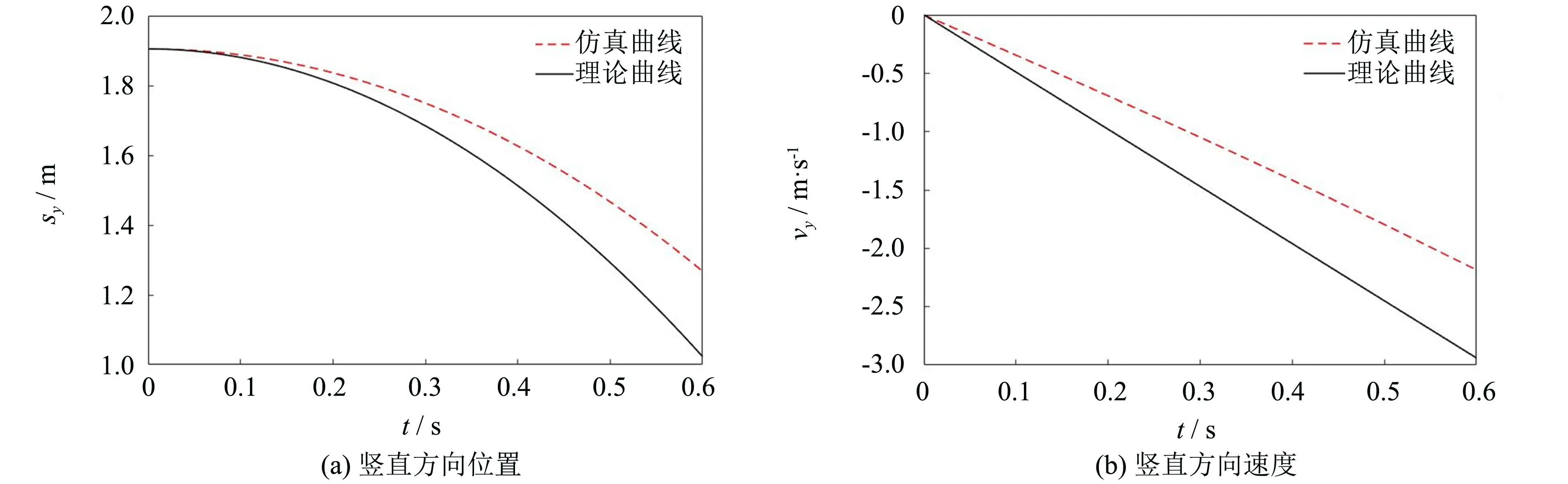
图4 0.5g重力补偿后航天员自由落体运动曲线Fig.4 Free fall motion curve of astronaut after 0.5g gravity compensation

为验证航天员动力学特性与微低重力模拟系统运动部件质量及关节摩擦力矩是否有关， 分别探究运动部件质量和关节摩擦对航天员动力学特性的影响， 设计两组仿真实验， 实验工况如表1所示. 为防止仿真系统动力学方程奇异， 系统质量及关节摩擦最低设置为原来的0.001倍， 仿真结果如图5所示.

表1 不同构件质量及关节摩擦工况设置

图(5)中， (a)、 (b)为系统各运动部件质量保持不变， 将关节摩擦变为原来的0.001倍后的仿真实验结果； (c)、 (d)为系统关节摩擦不变， 系统运动部件质量变为原来的0.001倍后的仿真实验结果； (e)、 (f)为系统关节摩擦和运动部件质量均变为原来的0.001倍后的仿真实验结果. 对比图5(a)、 (e)及图5(b)、 (f)可得， 关节摩擦对航天员动力学特性存在影响， 在竖直方向和水平方向均减缓航天员的运动， 但影响较小， 竖直方向约占总误差的1/5， 水平方向约占总误差的1/15. 对比图5(c)、 (e)及图5(d)、 (f)可得， 实验装置运动构件惯性对航天员动力学特性影响较大， 表现为减缓航天员竖直方向运动， 增加水平方向运动， 竖直方向误差约占总误差的4/5， 水平方向误差约占总误差的14/15. 从图5(e)、 (f)可以看出， 当重力补偿装置运动部件质量和关节摩擦变为原来的0.001倍时， 航天员经该装置重力补偿后， 其自由落体运动曲线与航天员在该重力条件下的理论自由落体运动曲线几乎吻合， 证明了系统运动部件质量和关节摩擦在一定程度上影响了失重模拟装置的动力学特性， 但总体上影响较小.

图5 构件质量及摩擦对航天员自由下落运动的影响Fig.5 Influence of component mass and friction on astronaut's free fall

针对重力补偿装置存在惯性导致动力学特性与理论存在差别这一问题， 提出以下几种解决办法.

1) 在安全许可范围内， 尽可能降低各运动部件质量， 如优化结构设计、 使用轻质材料等.

2) 通过外加主动系统的方法对系统存在的惯性和关节摩擦进行补偿， 如在关节处增加力矩电机并通过特定算法控制电机输出力矩， 实现系统惯性补偿和关节摩擦补偿.

3.3 航天员月面跳跃运动仿真

航天员在月球表面移动过程中， 主要通过跳跃的方式前进， 为保证航天员安全、 顺利完成在月任务， 需要对航天员在月球表面跳跃的运动情况进行模拟分析， 并验证重力补偿系统辅助完成航天员月面跳跃训练任务的可行性. 此次仿真以航天员在月球表面深蹲跳为例， 航天员在月面深蹲跳跃过程与地面深蹲跳跃过程一样， 有下蹲、 起跳、 腾空、 落地过程， 而且航天员的腿部发力方式也相同[24-25]. 为精确模拟跳跃过程， 需要知道航天员从下蹲到起跳过程中地面对航天员的支撑力， 在下蹲到起跳过程中地面支撑力、 重力和加速度关系式可表示为

式中：Fs为航天员与地面环境的交互力即地面支撑力，G为航天员所受重力，mb为航天员体质量，a为航天员从下蹲到起跳过程中的弹跳加速度， 该值仅与跳跃人员自身弹跳性能有关， 但不同人员间a相差不大， 可使用实验人员的弹跳性能初步代替航天员弹跳性能， 因为a仅与航天员弹跳性能有关， 在地面实验得到的弹跳加速度值适用于月球表面. 支撑力测量实验简图如图6所示， 实验过程中， 实验人员在压力传感器上做深蹲跳跃动作， 压力传感器实时记录支撑力值， 实验中实验人员体质量为77.5 kg， 重力加速度g=9.8 m·s-2.

图6 航天员支撑力测量实验简图 Fig.6 Schematic diagram of astronaut support force measurement experiment

经实验测量， 实验人员所受支撑力Fs及弹跳加速度a如图7(a)、 (b)所示， 为得到连续函数， 使用3次多项式对支撑力样本点进行拟合， 图7(c)、 (d)为实验人员质心速度与质心位置曲线. 由图7(a)、 (b)知， 实验人员在下蹲过程中， 属于部分失重状态， 地面压力减小； 从7(c)、 (d)图知， 当时间t=0.7 s时， 下降加速度为0， 航天员质心向下运动的速度达到最大，t=1 s时， 航天员速度为0， 航天员质心到达最低点， 此时进入起跳过程， 随着起跳时间增加， 地面支撑力增加， 当脚底离开地面时， 支撑力变为0， 随后进入腾空过程.

图7 地面深蹲跳实验Fig.7 Jump experiment on the earth

因航天员弹跳加速度a只与其弹跳性能有关， 故在月跳跃时， 其质心弹跳加速度与在地弹跳加速度a相同， 根据式(13)并结合月球重力加速度gy=1.633 3 m·s-2, 可计算得到航天员在月跳跃时地面对航天员的支撑力， 计算结果如图8(a)所示(仅绘出一个周期的图)， 从图中可以看出， 航天员在月跳跃时其受地面支撑力与在地跳跃所受支撑力具有相同的趋势， 但总体比在地球上跳跃受力小. 基于该受力曲线， 即可将该力带入式(11)的微低重力模拟系统动力学方程中进行动力学仿真， 仿真获取航天员在地模拟月面跳跃的整个运动过程. 仿真参数中， 设置航天员体质量为77.5 kg，ρ=0.83， 其他动力学参数与前文相同， 不考虑系统运动部件和关节摩擦与航天员间的动力学耦合， 设置系统的运动部件质量和关节摩擦为原来的0.001倍， 仿真结果如图8所示.

图8 失重模拟装置模拟航天员月面跳跃过程Fig.8 The weightlessness simulator simulates the astronaut's lunar jump process

图8(b)为失重模拟装置两关节转角变化曲线， 在跳跃过程中， 关节转角无突变； 图8(c)、 (d)中仿真曲线为航天员经失重模拟装置重力补偿后向上跳跃时竖直和水平方向的位移曲线， 理论曲线为航天员在月球重力条件下跳跃时竖直方向和水平方向的位移曲线. 从图中可知， 航天员首先下蹲， 其质心下移， 随后起跳并腾空， 在竖直方向上， 经失重模拟装置重力补偿后的航天员位移曲线与理论的位移曲线几乎重合； 在水平方向上， 因系统仍存在较小的惯性和关节摩擦， 故航天员垂直上跳时， 经重力补偿后的航天员水平位移值与理论值存在0.001 3 m的位移误差. 综上， 所有误差均在可接受范围内， 该失重模拟装置能很好地满足航天员月面跳跃训练， 为登月工作做好铺垫.

4 结语

研究设计了一种基于势能守恒的微低重力模拟系统. 该系统具有结构简单、 制造维护成本低、 可模拟0～1g任意重力环境且调节方便、 运动自由度不受限、 应用领域广等优点， 能满足未来繁多的空间任务验证和航天任务操作技能训练需求.

对低重力模拟系统重力卸载性能进行了仿真分析， 结果表明系统能很好地实现静态补偿， 较好地实现动态补偿.

针对动态补偿存在误差的问题， 分别对装置运动部件质量和关节摩擦对系统动态性能的影响进行仿真分析， 仿真表明， 在自由落体运动中， 竖直方向上关节摩擦导致的误差约为总误差的1/5， 部件质量导致的误差约为总误差的4/5， 水平方向上关节摩擦导致的误差约为总误差的1/15， 部件质量导致的误差约为总误差的14/15. 为消除误差， 提出了两种解决办法： 1) 优化结构设计； 2) 采用外部力矩输入的方式对关节轴承摩擦力和系统惯性力进行主动控制补偿.

对航天员月面跳跃任务工况进行仿真验证， 仿真结果表明， 经失重模拟装置重力补偿后的航天员跳跃时运动曲线与理论曲线误差很小， 能很好满足航天员月面跳跃训练需求.