广义Brandt半群的另一类Cayley图

李映辉 ， 王守峰

(1. 昆明学院教师教育学院, 云南 昆明 650204； 2. 云南师范大学数学学院, 云南 昆明 650500)

0 引言

研究半群Cayley图， 通常是利用图的组合性质刻画半群的结构， 或利用半群的代数结构刻画图的组合性质， 从而建立起图论与半群理论之间的联系. 半群Cayley图的研究可追溯到文献[1]， 2003年文献[2]中首次研究了半群上Cayley 图的点传递性. 受此启发和鼓舞， 众多学者展开了半群Cayley图的研究. 文献[3]研究了特殊半群(逆半群、 完全0-单半群)上的Cayley 图的结构和性质. Brandt半群是一类重要的半群， 是完全0-单的逆半群. Brandt半群上的Cayley图得到了许多学者的重视. 文献[4-6]研究了Brandt半群上以Geeen等价类为连接集的Cayley 图及其同构条件.

文献[7]首次给出了广义Brandt半群的代数结构， 是完全0-单的纯正半群. 本研究的目的是利用这一代数结构在文献[8]的基础上， 拓广Cayley图连接集及导出子集， 研究广义Brandt半群上分别以SIλ-、S-Jλ和SIλJλ为连接集的Cayley图. 通过对连接集为L-类、R-类和H-类等三类Green等价类在广义Brandt半群上的Cayley图间的同构条件的讨论， 刻画了这三类Cayley图的结构.

1 预备知识

对有向图Γ=(V，E)，V′⊆V，Γ=(V，E)的一个以V′作为顶点集， 以两个端点都属于V′的在原图Γ=(V，E)中的弧作为弧集的子图被称为V′导出子图， 记作Γ(V′).对于任意的正整数m，n， 完全图Km是指有m个顶点， 其中每个顶点都与其他顶点连接的图；nKm是n个完全图Km复制的不交并.一个r-部图是指一个图的顶点被分成r个子集V1，V2， …，Vr的不交并， 且在同一个子集中的任两点不连接； 完全r-部图是一个所有来自不同子集的任意两点均连接的r-部图.特别地， 完全二部图的顶点集是V=V1∪V2， 若|V1|=m，|V2|=n， 则记为Km， n， 而K1， n称为星图.对两个有向图Γ1=(V1，E1)和Γ2=(V2，E2)， 图同态φ:Γ1→Γ2是一个满足： (u，v)∈E1⟹(φ(u)，φ(v))∈E2的映射φ:V1→V2； 若映射φ:Γ1→Γ2是个双射， 且φ和φ-1都是图同态， 则称φ为图Γ1到Γ2同构映射， 此时称图Γ1与Γ2同构， 记作Γ1≅Γ2； 图同态φ:Γ→Γ称为自同态， 图同构φ:Γ→Γ称为自同构.文中未说明的术语和符号， 可参考文献[9-10].

设S是半群，A是S的子集， 定义Cayley图Cay(S，A)如下： 其顶点集V(Cay(S，A))=S， 对任意顶点u，v∈S， 称(u，v)(或者u～v)是Cay(S，A)的一条边， 如果存在a∈A， 使得v=au.即边集为：

E(Cay(S，A))={(s，as):s∈S，a∈A}

集合A称为Cayley图Cay(S，A)的连接集， 若A是空子集， 则Cayley图Cay(S，A)是空图.因此在本研究中设A是S的非空子集.据文献[10]， 半群S的以下Green等价关系成立.对任意的a，b∈S， 有：

aLb⟺S1a=S1b；aRb⟺aS1=bS1

记H=L∩R.易见， 对任意的a，b∈S，aLb当且仅当a=b或者存在x，y∈S， 使得a=xb和b=ya.对关系R和H也有类似结果.

完全0-单的纯正半群称为广义Brandt半群. Yamada在文献[7]中给出的这类半群的如下结构定理.

定理1[7]设G0是一个0-群(在群G上添加0元得到的半群).I和J是非空集，P=(pji)是一个J×I-矩阵， {Iλ:λ∈Λ}和{Jμ:μ∈Λ}分别是集合I和J的不交子集族(其中Λ是一个指标集)， 且满足下列条件：

2) 对任意的λ，μ∈Λ和j∈Jμ，i∈Iλ， 有：

则S=(I×G×J)∪{0}关于下列运算：

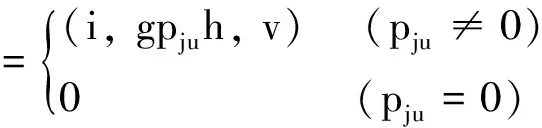
构成广义Brandt半群， 记之为S=M0(I，J;G;P;Λ).反之， 任何广义Brandt半群均可如此构造.

以下恒设S=M0(I，J;G;P;Λ)是广义Brandt半群.

2 主要定理与结果

本节讨论广义Brandt半群S关于L-类、R-类和H-类的Cayley图.对于给定的λ，μ∈Λ有Iλ，Jμ记:

S-Jμ={(i，g，j):i∈I，g∈G，j∈Jμ}，SIλ-={(i，g，j):i∈Iλ，g∈G，j∈J}

则S-Jμ，SIλ-分别是S的所有L-类和R-类.

2.1 广义Brandt半群关于L-类S-Jμ的Cayley图

命题1设A⊆S， (u，g，v)， (s，h，t)∈S， 且u∈Iλ， 则在广义Brandt半群S的Cayley图Cay(S，A)中， (u，g，v)～(s，h，t)当且仅当v=t且存在j∈Jλ， 有: (s，hg-1，j)∈A.

证明 充分性显然.

下证必要性： 设(u，g，v)～(s，h，t)，u∈Iλ， 则存在(i，x，j)∈A， 其中j∈Jλ， 使(s，h，t)=(i，x，j)(u，g，v)， 这表明pju=1，s=i，v=t且x=hg-1.于是有(s，hg-1，j)∈A.

推论1设(u，g，v)， (s，h，t)∈S， 在广义Brandt半群S关于L- 类S-Jμ的Cayley图Cay(S，S-Jμ)中， (u，g，v)～(s，h，t)当且仅当v=t，u∈Iμ， 而(u，g，v)～0当且仅当u∉Iμ.

命题2在广义Brandt半群S的Cayley图Cay(S，S-Jμ)中， 有以下结论：

① 对任意v∈Jμ， 由Iμ×G×{v}的导出子图是完全图K|Iμ||G|；

② 若λ≠μ(λ=μ)， 则由SIλ-导出的子图是空图(K|Iλ||G|)；

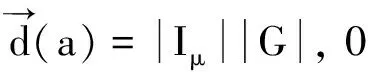
证明 ① 任取两点(s，g，v)， (t，h，v)∈Iμ×G×{v}， 因为v∈Jμ，s，t∈Iμ， 根据命题1， 总存在(t，hg-1，v)∈S-Jμ和(s，gh-1，v)∈S-Jμ， 使得pvs=1和pvt=1， 那么(t，h，v)=(t，hg-1，v)(s，g，v)和(s，g，v)=(s，gh-1，v)(t，h，v)成立.而|Iμ×G×{v}|=|Iμ||G|， 所以Cayley图Cay(S，S-Jμ)由Iμ×G×{v}的导出子图是完全图K|Iμ||G|.

② 如果λ≠μ， 对于任意的i1，i2∈Iλ， (i1，g，u)， (i2，h，u)∈SIλ-， 在连接集S-Jμ中找不到任何元使(i1，g，u)～(i2，h，u)成立， 所以Cayley图Cay(S，S-Jμ)由SIλ-的导出子图是空图； 如果λ=μ， 对于任意的(i1，g，u)， (i2，h，u)∈SIμ-， 由式(1)知， 总存在pj1i1=1和pj2i2=1， 且(i2，hg-1，j1)， (i1，gh-1，j2)∈S-Jμ， 使得: (i1，g，u)～(i2，h，u)和(i2，h，u)～(i1，g，u)成立， 所以Cay(S，S-Jλ)由SIλ-的导出子图是完全图K|Iλ||G|.

③ 当u∈Iμ时， 对任意(i，x，j)∈S-Jμ， 有pju=1， 这表明顶点a=(u，g，v)出度为:

=|{(i，y，v):i∈I，y∈G}|=|I||G|

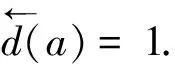
④ 考虑顶点a=(u，g，v)的入度， 首先pjs=1，有：

考虑0的入度， 由③的证明知只需讨论u∉Iμ的情形:

=|{(u，g，v):u∉Iμ，g∈G，v∈J}∪{0}|

=|{(u，g，v):u∉Iμ，g∈G，v∈J}|+1=(|I|-|Iμ|)|G||J|+1

定理2设λ，μ∈Λ， 则广义Brand半群S的两个L-类S-Jλ和S-Jμ的Cayley图Cay(S，S-Jλ)与Cay(S，S-Jμ)同构当且仅当|Iλ|=|Iμ|.

充分性： 若λ=μ， 显然成立.若λ≠μ， 由于|Iλ|=|Iμ|， 可设ψλ， μ:Iλ→Iμ是一个双射， 定义映射φ:S→S， 规定0φ=0， 对于任意的a=(u，x，v)， 有:

显然φ是一个双射， 下证φ是一个图同态.设a=(u，g，v)，b=(s，h，t)∈S且在Cayley图Cay(S，S-Jλ)中有a～b.下面分情况讨论.

情形1a=0，b=0.此时aφ=bφ=0， 在Cayley图Cay(S，S-Jμ)中自然有0～0， 即aφ～bφ.

情形3a≠0且b≠0.由于在Cayley图Cay(S，S-Jλ)中a～b， 必有u∈Iλ， 那么aφ=(uψλ， μ，x，v)，uψλ， μ∈Iμ， 而bφ=(s，y，v)φ=(*，y，v)， 再次根据推论1， 在Cayley图Cay(S，S-Jμ)中， 连接集中存在(*，yx-1，l)∈S-Jμ， 使得:(*，y，v)=(*，yx-1，l)(uψλ， μ，x，v).其中，pl， uψλ， μ=1， 即aφ～bφ.完全可以类似证明φ-1也是一个图同态.

综上所述， 有Cay(S，S-Jλ)≅Cay(S，S-Jμ).证毕.

2.2 广义Brandt半群S关于R-类SIλ-的Cayley图

命题3在广义Brandt半群S关于R-类SIλ-的Cayley图Cay(S，SIλ-)中， 下列结论成立：

Ⅰ) 对于任意顶点(u，g，v)， (s，h，t)∈S， 则(u，g，v)～(s，h，t)当且仅当v=t和s∈Iλ；

Ⅱ) 顶点0的出度是1.当|Λ|=1(|Λ|≥2)时， 顶点(u，g，v)的出度为:|Iλ||G|(|Iλ||G|+1)；

Ⅲ) 当|Λ|=1(|Λ|≥2)时， 顶点0的入度是1(|S|)；

Ⅳ) 若u∉Iλ(u∈Iλ)， 则顶点(u，g，v)的入度为0(|I||G|).

证明 Ⅰ) 由命题1立得.

=|{(i，x，j)(u，g，v):i∈Iλ，j∈Jμ，x∈G}∪{(i，x，j)(u，g，v):i∈Iλ，j∈Jγ，x∈G}|

=|{(i，y，v):i∈Iλ，y∈G}∪{0}|=|Iλ||G|+1

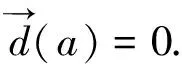
=|{(s，h-1g，v):s∈I，h∈G}|=|I||G|

定理3广义Brandt半群S的Cayley图Cay(S，Si-)由S-Jλ的导出子图Cay(S-Jλ，Si-)是同构于一个完全二部图Krn， n与一个星图K1， (m-r)n的并图Γ1.其中，m=|I|，r=|Iλ|，n=|G|.

证明 在广义Brandt半群S的Cayley图Cay(S，Si-)(i∈Iλ)由S-Jλ的导出子图Cay(S-Jλ，Si-)中， 依据命题3中Ⅰ)， 分两方面讨论：

一方面，u∈Iλ， 对任意(u，x，j1)∈S-Jλ， 存在(i，g，j2)∈Si-， 使得:(u，x，j1)～(i，gx，j1).根据命题3中Ⅱ)有:|{(u，x，j1):u∈Iλ，x∈G，j1∈Jλ}|=|Iλ×G×{j1}|=|Iλ||G|=rn， |{i}||G||{j1}|=|G|=n， 根据广义Brandt半群S的Cayley图定义， Cayley图Cay(S-Jλ，Si-)同构于一个完全二部图Krn， n.

另一方面，u∉Iλ， 对任意(u，x，j1)∈S-Jλ， 在广义Brandt半群S的Cayley图Cay(S，Si-)(i∈Iλ)由S-Jλ的导出子图Cay(S-Jλ，Si-)中， 均有: (u，x，j1)～0， 此时Cayley图Cay(S-Jλ，Si-)同构于一个星图K1， (m-r)n.

综上所述， Cay(S-Jλ，Si-)同构于一个完全二部图Krn， n与一个星图K1， (m-r)n的并图， 即:

Cay(S-Jλ，Si-)≅Krn， n+K1， (m-r)n=Γ1

定理4广义Brandt半群S的Cayley图Cay(S，SIμ-)由S-Jλ的导出子图Cay(S-Jλ，SIμ-)同构于t个完全二部图tKrn， n与一个星图K1， (m-r)n的并图， 即Cay(S-Jλ，SIμ-)≅tKrn， n+K1， (m-r)n=Γ2.其中m=|I|，r=|Iλ|，t=|Iμ|和n=|G|.

证明 在定理3的证明过程中， 注意到在Cayley图Cay(S，SIμ-)由S-Jλ的导出子图Cay(S-Jλ，SIμ-)中， |Iμ|=t， 当u∈Iλ时， 每个顶点的出度是在Cayley图Cay(S-Jλ，Si-)中的t倍.所以导出子图Cay(S-Jλ，SIμ-)同构于t个完全二部图tKrn， n与一个星图K1， (m-r)n的并图， 即:

Cay(S-Jλ，SIμ-)≅tKrn， n+K1， (m-r)n=Γ2

作为以上定理的推广， 有如下系列结论.

定理5ⅰ) 对于j∈Jλ，k∈Jγ， 那么Cayley图Cay(S，Si-)由S-j和S-l的两个导出子图Cay(S-j，Si-)与Cay(S-k，Si-)同构的充分必要条件是|Iλ|=|Iγ|;

ⅱ) 对于任意λ，γ∈Λ， Cayley图Cay(S，Si-)分别由S-Jλ和S-Jγ导出的两个子图Cay(S-Jλ，Si-)与Cay(S-Jγ，Si-)同构的充分必要条件是|Iλ|=|Iγ|;

ⅲ)对于任意λ，γ，μ∈Λ， 那么Cayley图Cay(S，SIμ-)分别由S-Jλ和S-Jγ导出的两个子图Cay(S-Jλ，SIμ-)与Cay(S-Jγ，SIμ-)同构的充分必要条件是|Iλ|=|Iγ|.

2.3 广义Brandt半群关于H-类的Cayley图

对于集合SIλJμ={(i，g，j):i∈Iλ，g∈G，j∈Jμ}， 若λ≠μ， 则不构成H-类， 所以本节讨论广义Brandt半群关于H-类SIλJλ的Cayley图Cay(S，SIλJλ).

命题4在广义Brandt半群S关于H-类SIλJλ的Cayley图Cay(S，SIλJλ)中， 设a=(u，g，v)，b=(s，h，t)∈S， 下列结论成立：

a) (u，g，v)～(s，h，t)当且仅当v=t，s，u∈Iλ， 而(u，g，v)～0当且仅当u∉Iλ;

b) 顶点0的出度为1， 当u∈Iλ时， 顶点a的出度为|Iλ||G|； 当u∉Iλ时， 顶点a的出度为1;

c) 顶点0的入度是:(|I|-|Iλ|)|G||J|+1.当u∉Iλ(u∈Iλ)时， 顶点a的入度为0(|Iλ||G|).

证明 a) 根据命题1直接得证.

=|{(i，y，v):i∈Iλ，y∈G}|=|Iλ||G|

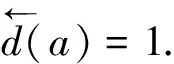
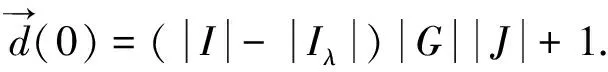
=|{(s，x-1g，v):s∈Iλ，x∈G}|=|Iλ||G|

同时，Pjs=1成立.

命题5广义Brandt半群S关于H-类SIλJλ的Cayley图Cay(SIλ-，SIλJλ)与一个左群Iλ×G的Cayley图Cay(Iλ×G，Iλ×G)同构.而左群的Cayley图Cay(Iλ×G，Iλ×G)同构于一个完全图Krn.其中， |Iλ|=r和|G|=n.

证明 在Cayley图Cay(SIλ-，SIλJλ)中， 因为对任意(u，x，j)， (v，y，j)∈SIλ-， 总存在(v，yx-1，j1)∈SIλJλ和(u，xy-1，j2)∈SIλJλ， 由于u，v∈Iλ，j1，j2∈Jλ，pj1u=1，pj2v=1使得:(v，y，j)=(v，yx-1，j1)(u，x，j)和(u，x，j)=(u，xy-1，j2)(v，y，j)成立.即(u，x，j)～(v，y，j)和(v，y，j)～(u，x，j)， 对应在一个左群Iλ×G的Cayley图Cay(Iλ×G，Iλ×G)中， 当且仅当对任意(u，x)， (v，y)∈Iλ×G， 在连接集中总存在(v，yx-1)， (u，xy-1)∈Iλ×G， 使得:(u，x)～(v，y)和(v，y)～(u，x).保持点的邻接关系， 所以映射:φ:(u，x，j)(u，x)是一个从Cayley图Cay(SIλ-，SIλJλ)到左群Iλ×G的Cayley图Cay(Iλ×G，Iλ×G)的图同构映射， 故Cay(SIλ-，SIλJλ)与Cay(Iλ×G，Iλ×G)同构.

而在左群Cayley图Cay(Iλ×G，Iλ×G)中， 对任一(u，x)∈Iλ×G， 因为|Iλ×G|=|Iλ||G|=rn总存在rn个点(v，y)∈Iλ×G， 使得: (u，x)～(v，y)， 所以Cayley图Cay(Iλ×G，Iλ×G)同构于完全图Krn.

定理6广义Brandt半群S关于H-类SIλJλ的Cayley图Cay(S，SIλJλ)与完全图Krn和星图Γ1， (m-r)n的并图同构.其中|Iλ|=r和|G|=n.

证明 因为指标集I=Iλ∪IIλ， 由命题5知Cay(SIλ-，SIλJλ)≅Krn， 所以下式成立：

Cay(S，SIλJλ)≅Cay(SIλ-，SIλJλ)+Γ1， (m-r)n≅Krn+Γ1， (m-r)n

定理7广义Brandt半群S的两个Cayley图Cay(S，SIλJλ)与Cay(S，SIμJμ)同构当且仅当|Iλ|=|Iμ|.

证明 设|I|=m， |Iλ|=r， |Iμ|=s以及|G|=n， 根据定理6有: Cayley图Cay(S，SIλJλ)≅Krn+Γ1， (m-r)n和Cayley图Cay(S，SIμJμ)≅Ksn+Γ1， (m-s)n.所以Cay(S，SIλJλ)≅Cay(S，SIμJμ)， 当且仅当r=s， 即|Iλ|=|Iμ|.

3 结语

本研究在文献[8]广义Brandt半群上分别以Si-,S-j和Sij为连接集的Cayley图的研究基础上， 拓广Cayley图连接集及导出子集， 讨论了广义Brandt半群上分别以SIλ-，S-Jλ和SIλJλ为连接集的Cayley图.通过对连接集为L-类，R-类和H-类等三类Green等价类在广义Brandt半群上的Cayley图间的同构条件的讨论， 刻画了这三类Cayley图的结构， 揭示了广义Brandt半群是一个完全0-单的纯正半群的本质特征， 突出了研究方法的系统化.