有向图最小圈长不大于4的一个充分条件

梁 浩, 徐俊明

(1. 西南财经大学 经济数学学院, 成都 611130； 2. 中国科学技术大学 数学科学学院, 合肥 230026)

设G=(V,E)是简单有向图(即不含环和平行边), 其中:V=V(G)表示G的顶点集;E=E(G)表示G的边集.

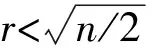
猜想1中, 对于r=n/3这一特殊情形受到了较多的关注： 当含有n个顶点的有向图中顶点的最小出度不小于n/3时, 图中一定存在长度不大于3的有向圈. 由于简单有向图不含环和平行边, 此时图中一定存在有向三角形. 这一简单猜想至今仍然未被证明, 于是人们考虑从另一个方向给出一些近似结果, 即寻找一个尽可能小的常数α, 使得当最小出度不大于αn时, 图中一定存在长度不大于3的有向圈, 即猜想1中的α=1/3. Caccetta等[1]证明了α<0.381 9时的结果, 之后文献[6-8]对其进行了改进. Hladk等[9]将该结果改进为α<0.346 5, 即任意含有n个顶点的有向图中顶点的最小出度不小于0.346 5n时, 图中一定存在长度不大于3的有向圈. 本文考虑尽可能小的常数α, 使得当最小出度不大于αn时, 图中必存在长度不大于4的有向圈, 猜想中α=1/4.

定理1若α≥0.288 66, 则n个顶点且最小出度不小于αn的有向图中一定存在圈长不大于4的有向圈.

对任意的顶点v∈V(G), 令N+(v)={u∈V(G): (v,u)∈E(G)}, deg+(v)=|N+(v)|称为v的出度；N-(v)={u∈V(G): (u,v)∈E(G)}, deg-(v)=|N-(v)|称为v的入度.

如果(u,v),(u,w),(v,w)∈E(G), 则称〈u,v,w〉是定向三角形. 其中(u,v)称为定向三角形的基, 顶点u称为定向三角形的源点. 如果(u,v),(v,w)∈E(G), 但u与w之间不连边, 则称uvw是长为2的导出子路. 对任意的(u,v)∈E(G), 令P(u,v)=N+(v)N+(u), 由定义可知p(u,v)=|N+(v)N-(u)|表示以(u,v)为第一条边长为2的导出子路的数目.Q(u,v)=N-(u)N-(v), 类似可知q(u,v)=|N-(u)N-(v)|表示以(u,v)为第二条边长为2的导出子路的数目.T(u,v)=N+(u)∩N+(v), 则t(u,v)=|N+(u)∩N+(v)|表示以(u,v)为基的定向三角形的数目.

引理1对任意的(u,v)∈E(G), 有

n>r+deg-(v)+q(u,v)+(1-α)r+(1-α)2t(u,v).

(1)

证明： 对(u,v)∈E(G), 当t(u,v)=0时, 不等式(1)简化为

n>r+deg-(v)+q(u,v)+(1-α)r.

(2)

在以N+(v)为顶点的导出子图中, 至少存在一个顶点w, 它在以N+(v)为顶点的导出子图中的出度小于αr. 否则由归纳假设可知, 在这个顶点数为r的导出子图中必存在长度不大于4的有向圈. 因此, |N+(w)N+(v)|≥r-αr. 再由假设条件,G中有向圈的长度都大于4, 可知N+(v),N+(w)N+(v),N-(v)及N-(u)N-(v)是两两不交的点集, 故有

n>|N+(v)|+|N-(v)|+|N-(u)N-(v)|+|N+(w)N+(v)|≥r+deg-(v)+q(u,v)+(1-α)r.

从而当t(u,v)=0时, 式(1)成立.

当t(u,v)>0时, 至少存在一个顶点w∈N+(u)∩N+(v), 在以N+(u)∩N+(v)为顶点的G的导出子图中,w的出度小于αt(u,v), 否则由归纳假设, 在此导出子图中必存在长度不大于4的有向圈, 故有

|N+(w)∩(N+(u)∩N+(v))|<αt(u,v).

(3)

另一方面,N+(w)包含于N+(v)N+(u)中的顶点数目满足

|N+(w)∩(N+(v)N+(u))|≤|N+(v)N+(u)|=p(u,v).

(4)

注意到t(u,v)=r-p(u,v), 综合式(3),(4)并代入

|N+(w)N+(v)|=|N+(w)|-|N+(w)∩(N+(u)∩N+(v))|-|N+(w)∩(N+(v)N+(u))|

可得

|N+(w)N+(v)|≥r-αt(u,v)-p(u,v)=(1-α)t(u,v).

(5)

由归纳假设,G中不含有向三角形, 故N+(w)N+(v),N-(u)N-(v),N-(v)是两两不交的点集. 考虑G中以N+(v)∪N+(w)为顶点的导出子图. 根据归纳假设, 存在顶点x∈N+(v)∩N+(w), 在此导出子图中,x的出度小于α|N+(v)∪N+(w)|. 于是N+(x)中落在N+(v)∪N+(w)以外的顶点数目满足

即

|N+(x)(N+(v)∪N+(w))|≥(1-α)r-α|N+(w)N+(v)|.

(6)

由于G中不含长为4的有向圈, 故N+(x)(N+(v)∪N+(w)),N-(u)N-(v),N-(v)也是两两不交的点集. 于是N-(v),N+(w)N+(v),N+(x)(N+(v)∪N+(w)),N-(u)N-(v),N-(v)为两两不交的点集, 其顶点数目分别为r,|N+(w)N+(v)|,|N+(x)(N+(v)∪N+(w))|,q(u,v)和deg-(v), 故

n>r+|N+(w)N+(v)|+|N+(x)(N+(v)∪N+(w))|+q(u,v)+deg-(v).

(7)

将式(5),(6)代入式(7)得

证毕.

下面证明定理1. 注意到t(u,v)=r-p(u,v), 将不等式(1)重写为

(2α-α2)t(u,v)>(3-α)r-n+deg-(v)+q(u,v)-p(u,v).

(8)

两端对所有的(u,v)∈E(G)求和, 可得

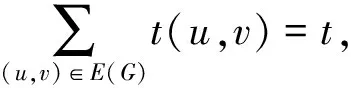
(9)

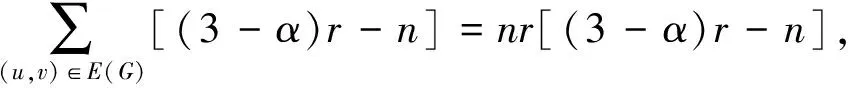
(10)

其中t表示G中定向三角形的数目. 再由Cauchy不等式得

即

(11)

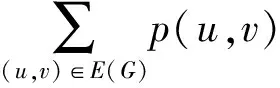
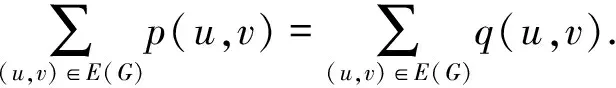
(12)

在式(8)两端对所有的(u,v)∈E(G)求和, 并将式(9)～(12)代入可得

(2α-α2)t>(4-α)nr2-n2r.

(13)

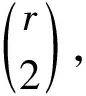
(14)

比较式(13),(14)有

(4-α)nr2-n2r<(nr2/2)(2α-α2).

(15)

[1] Caccetta L, Haggkvist R. On Minimal Digraphs with Given Girth [C]//Proc 9th S-E Conf Combinatorics, Graph Theory and Computing. Boca Raton: Utilitas Mathematica Publishing, Inc, 1978: 181-187.

[2] Hamidoune Y O. A Note on Minimal Directed Graphs with Given Girth [J]. J Combin Theory: Ser B, 1987, 43(3): 343-348.

[3] Hoang C, Reed B. A Note on Short Cycles in Digraphs [J]. Discrete Math, 1987, 66(1/2): 103-107.

[4] SHEN Jian. On the Girth of Digraphs [J]. Discrete Math, 2000, 211(1/2/3): 167-181.

[5] Sullivan B D. A Summary of Results and Problems Related to the Caccetta-Haggkvist Conjecture [J/OL]. 2006-05-24. http://arxiv.org/abs/math/0605646.

[6] Bondy J A. Counting Subgraphs: A New Approach to the Caccetta-Haggkvist Conjecture [J]. Discrete Math, 1997, 165/166: 71-80.

[7] SHEN Jian. Directed Triangles in Digraphs [J]. J Combin Theory: Ser B, 1998, 74(2): 405-407.

[8] Hamburger P, Haxell P, Kostochka A. On Directed Triangles in Digraphs [J]. Electronic J Combin, 2007, 14(1): 19.