基于分割的超树分解方法

王 涛, 王瑞芹, 李占山, 陈 超

(1. 长春工业大学 计算机科学与工程学院, 长春 130012；2. 吉林大学 符号计算与知识工程教育部重点实验室, 长春 130012; 3. 吉林大学 计算机科学与技术学院, 长春 130012)

约束满足问题(constraint satisfaction problem, CSP)[1]广泛应用于符号推理、 系统诊断、 配置和调度等问题中. 寻找一个约束满足问题的解是NP难问题[1], 目前已有很多优秀的CSP求解算法, 其中嵌入约束传播技术[2]的回溯算法[3]是一种应用较广泛的CSP求解算法. 为了处理CSP问题的高复杂性, 已产生了许多CSP分解方法, 其中超树分解是目前应用较多的一种方法. 它把CSP的结构表示成一个超图. 超图是一个图的泛化, 每条边都与一个变量集相关联. Gottlob等[4]提出了超图的超树宽度是对无环性的一个合适度量, 也是衡量对应计算问题是否为易处理问题的重要指标. 超树分解的宽度越小, 相应问题的处理效率越高. 决定一个超树分解的宽度是否为k是NP难题.

文献[4]指出, 对一个固定值k, 可在多项式时间内决定是否存在一个分解宽度为k的超树分解, 并提出了k-decomp算法[4]. 该算法可以构造一个极小宽度不大于k(k-bounded) 的超树分解(若这样的分解存在). 另一种计算极小宽度不大于k的超树分解方法是opt-k-decomp算法[5-9], 它是目前唯一能在多项式时间内精确构造k-bounded超树分解的算法, 但它即使对于小的超树也需要大量的存储空间和时间. Gottlob等[10]提出了一种基于回溯的超树分解算法det-k-decomp, 结合了精确算法和启发式算法的优点, 搜索空间和产生超树分解的宽度均由固定上限k限定, 即它可通过设置足够小的k找到具有极小宽度的超树分解. 该方法可以在产生的超树宽度和计算时间之间进行平衡. Subbarayan等[11]提出了基于回溯的超树分解算法, 并把部件同构的概念应用于算法中, 以加速算法的执行. 此外还提出了HyperSpread Decomposition和Connected HyperTree Decomposition算法, 并给出了实验结果, 证明了引入同构概念后Connected HyperTree Decomposition算法的优越性.

基于det-k-decomp算法思想, 本文把Sathiamoorthy的同构概念引入到det-k-decomp算法中, 提出一种新的易处理的分解方法： 基于分割的超树分解算法----sht-k-decomp.

1 定 义

一个约束满足问题(CSP)是一个三元组(X,D,C), 其中:X是一个有限变量集;D是一个有限值域集;C是一个有限约束集. 有限值域di∈D是变量xi∈X的取值集合, 每个约束ci∈C都对应一个X的子集si及一个关系ri, 其中ri是变量集si上的关系, 它限制了si中变量的取值范围. 若给si中所有变量一个赋值, 这些赋值的组合满足关系ri, 则称约束ci是可满足的. 一个CSP的解是对CSP中的所有变量赋值, 且这些赋值满足CSP中的所有约束.

一个CSP(X,C,D)的超图H是一个二元组(V,E), 其中:V是一个变量集, 对应于CSP的变量集X;E为超边的集合, 对E中的每个超边ei, 对应于CSP中的一个约束ci, 满足ei=si. 此外, 令vars(K)=∪e(e∈k), 其中K是超边集E的子集,K⊆E,

edges(L)={e|e∈E,e∩L≠Ø}, edgesvar(L)=vars(edges(L)),

其中L是变量集V的子集.

超图H(V,E)的超树是一个三元组(T,χ,λ), 其中T=(N,E)是一个树,N是T中节点的集合. 对超树T中的节点n∈N,χ(n)对应超图H中变量集V的一个子集,λ(n)对应超图H中超边集E的一个子集, 即

χ(n)⊆V,λ(n)⊆E.

T的子树

用root(T)表示T的根节点,T(n)表示T以n为根节点的子树.

一个超图H(V,E)的超树分解是一个超树(T,χ,λ), 其中T=(N,E), 满足如下条件[2]：

1) ∀e∈E, ∃n∈N满足e⊆χ(n);

2) ∀v∈V, 集合{n|n∈N,v∈χ(n)}可诱导出T的一个子树;

3) ∀n∈N,χ(n)⊆∪λ(n);

4) ∀n∈N, ∪λ(n)∩χ(T(n))⊆χ(n).

超树分解(T,χ,λ)的宽度为|λ(n)|, 其中n∈N是树T中包含超边数目最多的节点. 一个超图的超树宽度是该超图所有超树分解宽度的最小值, 记为htw(H). 若一个超图H的超树宽度htw(H)≤k, 则称超图H是k-decomposable的. 图1为一个超图及其宽度为2的超树分解.

对超图H=(V,E), 若存在超边e∈E, 满足x,y∈(∪e)W, 集合V′⊆V是[W]-connected的, 且V′中任意两个变量都关于W相邻, 则称变量x,y∈V关于变量集W⊆V相邻. 若一个[W]-component是一个极大的[W]-connected变量集V′⊆VW, 则称W为一个separator, 它对超图的超树分解十分重要. 本文用覆盖相应变量集的超边集合表示separator和[separator]-component.

定义1[4]若对T中的每个节点r及r的每个子节点s都满足以下条件, 则一个超图的超树分解(T,χ,λ)是规格化形式的:

1) 存在一个[χ(r)]-componentCr, 使得

χ(T(s))=Cr∪(χ(s)∩χ(r));

2)χ(s)∩Cr≠Ø, 其中Cr是满足条件1)的[χ(r)]-component;

3) ∪λ(s)∩χ(r)⊆χ(s).

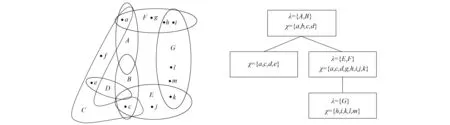
图1 一个超图及该超图宽度为2的超树分解示意图Fig.1 Example of a hypergraph and its hypertree decompositon of width 2

定义2[10]令(T,χ,λ)为超图的一个具有规格化形式的超树分解, 且s为T中的一个节点, 如果s满足下列条件, 则称s是极小标识的:

1) 若s=root(T), 则|λ(s)|=1;

2)s的父节点为r(存在相应[χ(r)]-componentCr满足

χ(T(s))=Cr∪(χ(s)∩λ(r)),

且满足对任意e∈χ(s),

∪edges(Cr)∩∪λ(r)⊄∪(λ(r){e})或(λ(r){e})∩edges(Cr)=Ø.

定义3[10]若一个超图的超树分解是规格化形式的, 且它的每个节点都是极小标识的, 则该超图的超树分解是强规格化形式的.

引理1[10]对超图H的任一个宽度为k的超树分解, 都存在一个相应强规格化形式宽度为k的超树分解.

2 Det-k-decomp算法

由det-k-decomp算法得到超图H的超树分解(若存在)是强规格化形式的.

算法1det-k-decomp(H).

FailSeps∶=Ø;

SuccSeps∶=Ø;

HTree∶=decompCov(edges(H),Ø);

if HTree≠NULL then

HTree∶=expand(HTree);

endif

return HTree.

算法2decompCov(Edges,Conn).

if |Edges|≤kthen

HTree∶=getHTNode(Edges,∪Edges,Ø);

return HTree;

endif

BoundEdges∶={e∈edges(H)|e∩Conn≠Ø}

for each CovSep∈cover(Conn,BoundEdges) do

HTree∶=decompAdd(Edges,Conn,CovSep)

if HTree≠NULL then

return HTree;

endif

endfor

return NULL.

算法3decompAdd(Edges,Conn,CovSep).

InCovSep∶=CovSep∩Edges

if InCovSep≠Ø ork-|CovSep|>0 then

if InCovSep=Ø then AddSize∶=1

else AddSize∶=0

endif;

for each AddSep⊆Edges s.t.|AddSep|=AddSize

do

Separator∶=CovSep∪AddSep;

Components∶=separate(Edges,Separator);

if ∀Comp∈Components.〈Separator,Comp〉∉FailSeps then

Subtrees∶=decompSub(Components,Separator);

if Subtrees≠Ø then

Chi∶=Conn∪∪(InCovSep∪AddSep);

HTree∶=getHTNode(Separator,Chi,SubTrees)；

return Htree;

endif

endif

endfor

endif

return NULL.

算法4decompSub(Components,Separator).

Subtrees∶=Ø

for each Comp∈Components do

ChildConn∶=∪Comp∩∪Separator

if 〈Separator,Comp〉∈SuccSeps then

HTree∶=getHTNode(Comp,ChildConn,Ø)

else

HTree∶=decompCov(Comp,ChildConn);

if HTree=NULL then

FailSeps∶=FailSeps∪ {〈Separator,Comp〉};

return Ø;

else

SuccSeps∶=SuccSeps∪{〈Separator,Comp〉};

endif

endif

Subtrees∶=Subtrees∪{HTree};

endfor

return Subtrees.

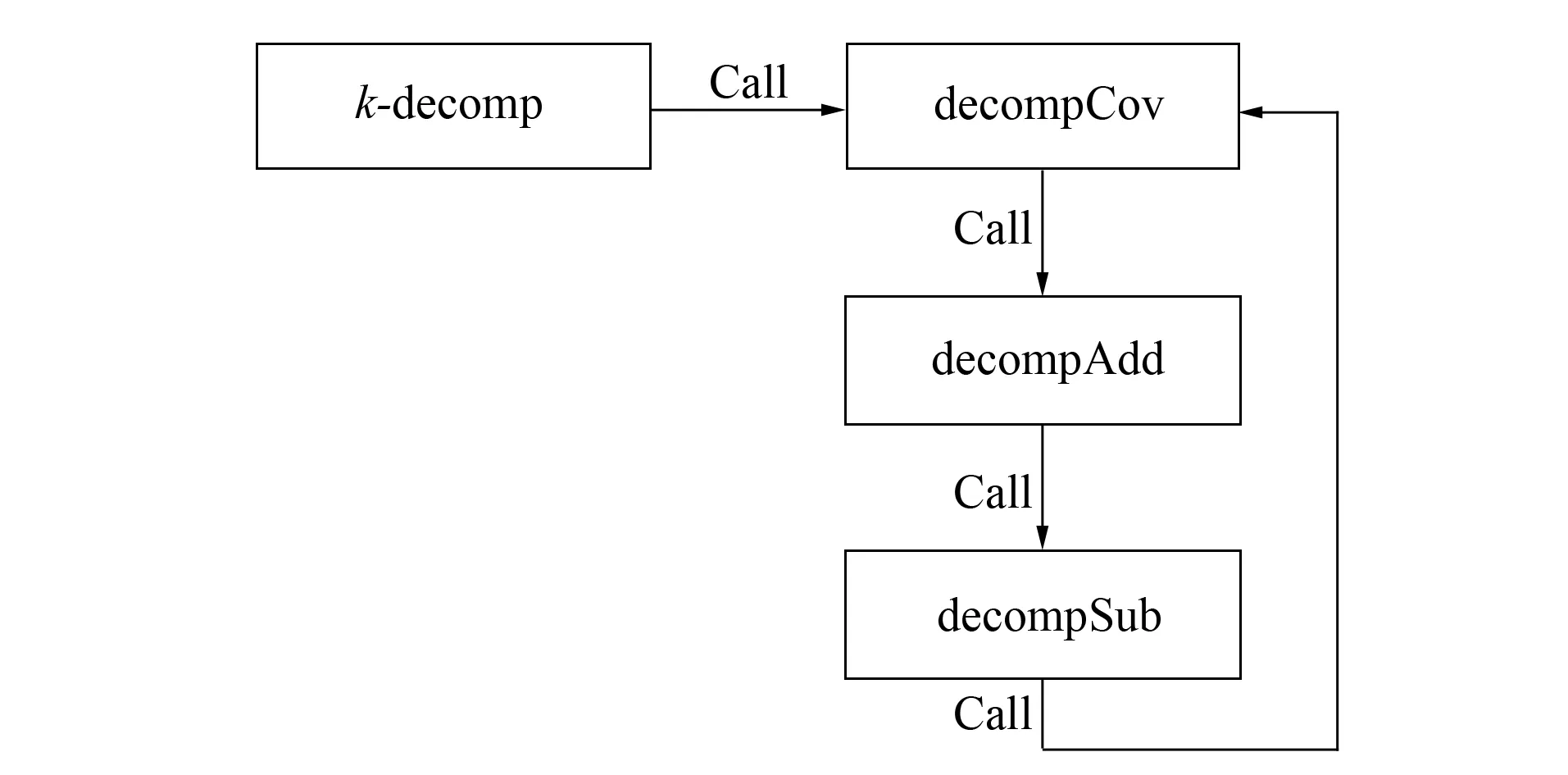
图2 Det-k-decomp各过程间的调用关系Fig.2 Procedure calls of det-k-decomp

算法1中, 集合FailSeps和SuccSeps中的元素是一个二元组〈Separator,Comp〉(这里称为待分解部件), 分别用于存放分解过程中分解失败的待分解部件和分解成功的待分解部件. 这样在分解过程中若已知当前待分解部件可成功分解, 则把当前待分解部件作为超树的截止节点； 否则, 返回, 不继续当前分解. det-k-decomp是主过程, 调用decompCov,decompAdd和decompSub过程对超图进行分解, 并返回分解得到的超树(若不存在, 返回空树). 在算法1的最后, 对分解得到的超树执行expand函数扩展分解过程中得到的截止节点. 算法2～算法4是递归调用过程, 完成对超图的分解. 各算法调用关系如图2所示.

该算法中, 最重要的是separator的选择. 对待分解超图, 先选择出作为分解基准的separator, 再找出待分解超图中所有的[separator]-component, 最后逐个迭代分解每个[separator]-component, 直到每个子超图都分解为宽度不大于k的超树为止.

每次选出的separator都应满足如下两个基本条件:

1) ∪Edges∩∪OldSep⊆∪separator;

2) separator∩Edges≠Ø.

其中: Edges是待分解超图(这里用超图的超边集合表示超图); OldSep是上次选出的separator. 算法4先对Childconn=∪Edges∩∪OldSep进行计算, 然后把Childconn作为参数传递给算法2. 算法2在超图中寻找与Conn(即Childconn)有共同变量的所有超边, 存放在集合BoundEdges中. 这样BoundEdges集合中就存放了所有与∪separator有交集的超边, 并且∪BoundEdges=∪separator. 因此, 可以考虑将超边集合BoundEdges中的超边作为separator, 以缩减separator的搜索空间. 首先, 从BoundEdges中选出一个最多有k个超边的子集CovSep, 使得Conn⊆∪CovSep, 且CovSep⊆separator. 该选择过程由Cover函数完成. Cover过程可返回所有的CovSep. 然后调用算法3, 在decompAdd过程中首先判断CovSep是否与待分解超图Edges有交集, 且是否|separator|≤k决定separator的最终取值, 得到的separator即满足上述两个基本条件.

选出满足条件的separator后, 在算法3中调用separate函数, 对待分解超图Edges进行分解, 并将分解得到的每个子超图Comp, 即[separator]-component, 放入集合components中. 然后判断components中是否存在已知不可分解的Comp, 若存在, 则重新选择separator； 否则, 调用decompSub过程对components中的所有Comp进行分解, 并调用getHTNode函数构造当前超树节点, 其中: Chi为此节点的χ标识; Separator为节点的λ标识; Subtrees为当前节点的子树集合.

算法4完成对当前分解得到的各个子超图的分解. 对每个子超图, 先计算出其与当前分解选出的separator的交集： Childconn作为分解该子超图时选择separator的依据; 再判断当前子超图是否已知可以成功分解, 若可以, 则把当前部件作为截止节点; 否则调用递归过程decompCov进行分解; 根据分解结果把当前部件存放到FailSeps或SuccSeps中; 最后返回分解得到的子树, decompSub过程结束.

在det-k-decomp算法中, Cover过程应用了一种启发式, 即首先按超边中包含的Conn中变量的个数给BoundEdges中的每条超边赋一个权值, 然后根据该权值, 从大到小进行排序, 最后基于这个顺序, 选择出所有可覆盖Conn的极小超边集CovSep.

由算法2可见, 在计算BoundEdges时, 是从超图的所有超边中选取. 但在许多超图例子中可以注意到： 对两个[OldSep]-component Edges和Edges′, ∪Edges∩∪OldSep∩∪Edges′≠Ø, 这样在对Edges进行分解时, 选取的separator可能会包含Edges′中的超边. 在多数情况下, Edges′的超边对Edges的分解没有实际作用, 甚至有时Edges′中超边的选取还会导致该次循环过程的失败返回. 因此, 本文提出了分割的超树分解----SHTD的概念.

3 分割的超树分解

定义4一个超图的分割的超树分解SHTD=(T,χ,λ), 满足如下条件：

1) 它是一个具有强规格化形式的超树分解;

2) 若对T中的每个节点r和r的子节点集合S, 满足∀si,sj∈S, 有

λ(si)∩λ(sj)⊆∪λ(r).

条件2)表明在选取下一个separator时, 只从OldSep和待分解的Edges中选取, 而不是从所有的超边中选取.

对det-k-decomp算法进行时间复杂度分析可知, 算法的时间主要是由decompCov算法的循环次数决定, 因此对BoundEdges集合的大小进行限制, 可减少InCover过程返回满足条件的CovSep数目, 进而减少CovSep的循环次数, 降低时间复杂度. 令超图H的分割的超树宽度为shtw(H), 可知htw(H)≤shtw(H). 若shtw(H)≤k, 则称超图H是s-k-decomposable的. 由于分割的超树分解是超树分解的一个子集, 因此分割的超树分解也是可处理的.

文献[8]中提出了同构的概念, 在其回溯的超树分解算法中, 待分解部分Comp是一个变量的集合, 而在det-k-decomp中则把该待分解部分Comp转化为edges(Comp), 这两种情况是等价的, 且

Comp=∪edges(Comp)∪OldSep.

若Comp=Comp′, 则称(OldSep,Comp)和(OldSep′,Comp′)是同构的. 文献[8]还证明了

Conn=∪edges(Comp)∩∪OldSep=∪edges(Comp)Comp

的选取与OldSep无关. 因为BoundEdges的取值是从所有超边中选取, 所以separator的选取也只与Conn和Comp有关, 与OldSep无关. 因此, 同构的两个部件可分解性也是等价的. 引入同构的概念, 可使递归运算极大减少.

基于上述分析, 本文提出基于分割的超树分解算法----sht-k-decomp算法. 该算法基于det-k-decomp算法思想, 并引入同构的概念, 舍弃一些对分解失败概率较大的子超图分解, 使分解效率得到提高. 需注意的是sht-k-decomp算法得到的超树分解并不一定是分割的超树分解.

4 Sht-k-decomp算法

算法5Sht-k-decomp(edges(H)).

FailSeps∶=Ø;

SuccSeps∶=Ø;

HTree∶=SdecompCov(vars(edges(H)),Ø,Ø);

if HTree≠NULL then

HTree∶=expand(HTree);

endif

return HTree.

算法6SdecompCov(Comp,Conn,OldSep).

if |edges(Comp)|≤kthen

HTree∶=getHTNode(edges(Comp),∪edges(Comp),Ø);

return HTree;

endif

InBoundEdges∶={e∈edges(Comp)∪OldSep|e∩Conn≠Ø}

for each CovSep∈Cover(Conn,InBoundEdges) do

HTree∶=SdecompAdd(Comp,Conn,CovSep,OldSep)

if HTre≠NULL then

return HTree;

endif

endfor

return NULL.

算法7SdecompAdd(Comp,Conn,CovSep,OldSep).

InCovSep∶=CovSep∩edges(Comp)

if InCovSep≠Ø ork-|CovSep|>0 then

if InCovSep=Ø then AddSize∶=1

else AddSize∶=0

endif;

for each AddSep⊆edges(Comp) s.t.|AddSep|=AddSize do

Separator∶=CovSep∪AddSep;

Components∶=separate(Comp,Separator);

if ∀SepComp∈Components.

〈Separator,SepComp〉∉FailSeps then

Subtrees∶=SdecompSub(Components,Separator,OldSep);

if Subtrees≠Ø then

Chi∶=Conn∪∪(InCovSep∪AddSep);

HTree∶=getHTNode(Separator,Chi,Subtrees);

return Htree;

endif

endif

endfor

endif

return NULL.

算法8SdecompSub(Components,separator,OldSep).

Subtrees∶=Ø

for each Comp∈Components do

ChildConn∶=∪edges(Comp)∩∪separator

if Comp∈SuccSeps then

HTree∶=getHTNode(Comp,ChildConn,Ø)

else

HTree∶=SdecompCov(Comp,ChildConn,separator);

if HTree=NULL then

FailSeps∶=FailSeps∪{〈OldSep,Comp〉};

return Ø;

else

SuccSeps∶=SuccSeps∪{Comp};

endif

endif

Subtrees∶=Subtrees∪{HTree};

endfor

return Subtrees.

本文算法基于det-k-decomp算法思想, 不同之处在于： 在sht-k-decomp算法中, 待分解部件是一个变量集合Comp, 而不是超边集合； 对separator的选择空间做了进一步限制, 主要体现在对与变量集Conn有公共变量的超边集(det-k-decomp算法中此集合为BoundEdges; sht-k-decomp算法中为InBoundEdges)的计算上. 此外, 在sht-k-decomp算法中本文引入了同构概念. 但在sht-k-decomp算法中, InBoundEdges的取值是与OldSep有关的, 所以separator的选取也与OldSep相关. 因此, 在sht-k-decomp算法中判断是否已知不为k-decomposable时, 就需要判断〈OldSep,Comp〉是否属于FailSeps, 而在判断是否已知是k-decomposable时, 可引入Sathiamoorthy的同构概念, 即只需判断〈comp〉是否与SuccSeps中的部件同构, 但这样得到的超树分解不一定是SHTD.

令由算法sht-k-decomp得到的超树分解宽度为sdhtw(H), 则htw(H)≤sdhtw(H).

定理1Sht-k-decomp返回一个基于分割的超树分解当且仅当sdhtw(H)≤k.

证明： sht-k-decomp是在det-k-decomp基础上进行改进的. 与det-k-decomp算法相同, sht-k-decomp是一个迭代过程, 在每次迭代中, 它会循环所有可能的分解情况, 即循环满足条件的separator并进行分解, 直到成功返回一个分解宽度至多为k的分割超树分解或在迭代循环完所有的separator后返回一颗空树. 因此, 若存在sdhtw(H)≤k的分割超树分解, sht-k-decomp过程则一定能找到这样的超树分解, 并成功返回.

表1列出了分别使用det-k-decomp算法和sht-k-decomp算法对图1中超图进行分解的对比结果.

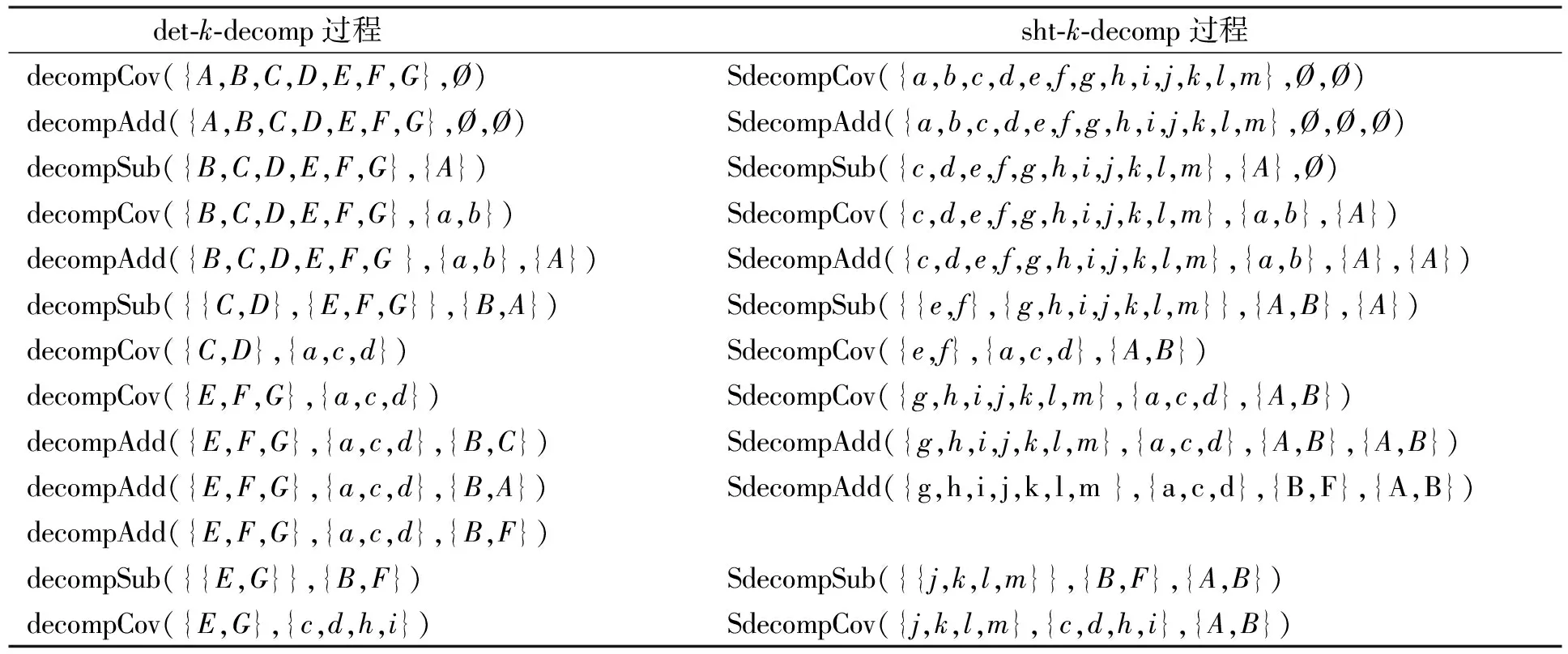
表1 Det-k-decomp和sht-k-decomp分解过程对比

由表1可见, 当Conn={a,c,d}时, det-k-decomp算法中计算得到的

BoundEdges={A,B,C,D,E,F},

其Cover函数可返回的CovSep顺序为{B,C},{A,B},{B,F},{C,E},{C,D},{A,E},{E,F}. 而对sht-k-decomp算法, 计算得到的InBoundEdges={B,E,A,F}, Cover函数可返回的CovSep顺序为{A,B},{B,F},{A,E},{E,F}. 对超图的分解, sht-k-decomp中会避免det-k-decomp中因CovSep取{B,C}而导致分解失败的情况. 这是较小的例子, 对较大的例子, 超边越多, 这种情况出现的几率就越大, 此时用sht-k-decomp会极大提高分解效率.

5 实验结果

本文使用文献[10]中的部分测试用例对det-k-decomp算法和sht-k-decomp算法进行对比. 测试环境为硬件DELL Intel Core 2 Duo 2.93 GHz CPU/2.0 Gb RAM； 软件Windows XP Professional SP2/Visual C++6.0. 每个用例测试10次, 取平均值作为最后结果.

在测试用例时, 本文设置时间限制为3 600 s, 并令k为不大于从det-k-decomp算法中已得到的最小分解宽度的值. 实验结果列于表2和表3. 表2和表3为在时间限制范围内得到的测试结果, 其中|V|和|E|分别为待分解超图包含的变量数和超边数. 对这两个算法, 用两组属性进行比较： 运行时间和最小分解宽度, 并把分解宽度作为最重要的对比标准. 在最小分解宽度相同的条件下, 运行时间越少, 算法运行效率越高.

表2 DaimlerChrysler和Grid2D标准库测试用例

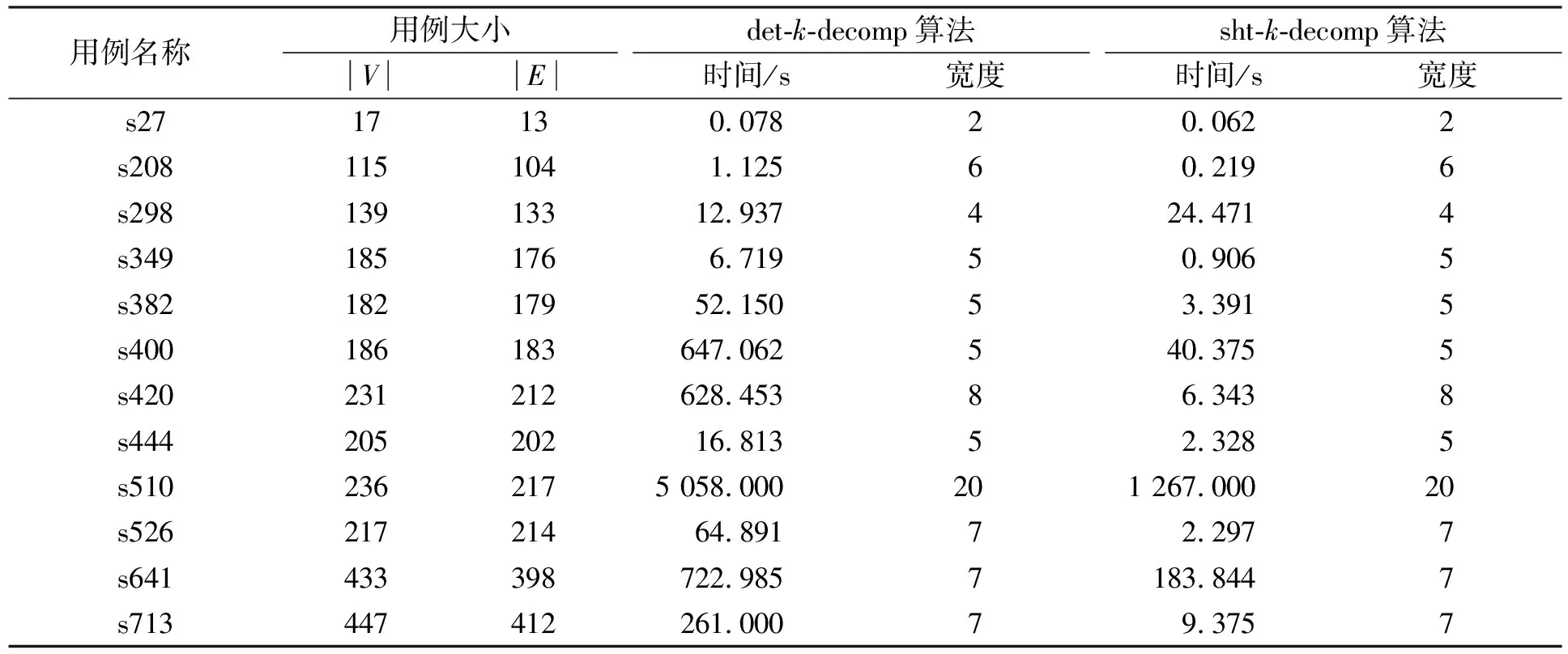
表3 ISCAS89标准库测试用例

由表2和表3可见, 对所有例子, sht-k-decomp算法得到的最小分解宽度与det-k-decomp算法的最小分解宽度相同, 且多数情况下sht-k-decomp算法的执行效率高于det-k-comp算法.

综上所述, 本文提出了一种新的超树分解方法： 分割的超树分解----SHTD, 并基于分割的超树分解所具有的特征提出了一种新的超树分解算法----基于分割的超树分解算法sht-k-decomp. 分割的超树分解是超树分解的子集, 它较易处理且htw(H)≤shtw(H). 算法sht-k-decompc通过进一步缩小separator的搜索空间和引入同构概念对算法det-k-decomp进行改进. 采用文献[10]部分用例进行测试, 结果表明在多数情况下, sht-k-decomp算法高于det-k-decomp算法的效率, 且对所有的例子它们的最优分解宽度相同.

[1] Freuder E C, Mackworth A K. Constraint Satisfaction: An Emerging Paradigm [C]//Handbook of Constraint Programming. Amsterdan: Elsevier, 2006: 13-27.

[2] Bessière C. Constraint Propagation [C]//Handbook of Constraint Programming. Amsterdan: Elsevier, 2006: 29-84.

[3] Beek P, Van. Backtracking Search Algorithms [C]//Handbook of Constraint Programming. Amsterdan: Elsevier, 2006: 85-134.

[4] Gottlob G, Leone N, Scarcello F. Hypertree Decompositions and Tractable Queries [J]. Journal of Computer and System Sciences, 2002, 64(3): 579-627.

[5] Gottlob G, Leone N, Scarcello F. On Tractable Queries and Constraints [C]//Proceedings of the 10th International Conference on Database and Expert System Applications (DEXA). London: Springer-Verlag, 1999: 1-15.

[6] Leone N, Mazzitelli A, Scarcello F. Cost-Based Query Decompositions [C]//Proceedings of the 10th Italian Symposium on Advanced Database Systems (SEBD). Portoferraio: [s.n.], 2002: 390-403.

[7] Scarcello F, Greco G, Leone N. Weighted Hypertree Decompositions and Optimal Query Plans [J]. Journal of Computer and System Sciences, 2007, 73(3): 475-506.

[8] Gottlob G, Leone N, Scarcello F. A Comparison of Structural CSP Decomposition Methods [J]. Artificial Intelligence, 2000, 124(2): 243-282.

[9] Harvey P, Ghose A K. Reducing Redundancy in the Hypertree Decomposition Scheme [C]//Proceedings of the 15th International Conference on Tools with Artificial Intelligence. LosAlamitos, CA: IEEE Computer Society, 2003: 474-481.

[10] Gottlob G, Samer M. A Backtracking-Based Algorithm for Hypertree Decomposition [J]. Journal of Experimental Algorimics (JEA), 2008, 13(1): Article No.1.

[11] Subbarayan S, Andersen H R. Backtracking Procedures for Hypertree, HyperSpread and Connected Hypertree Decomposition of CSPs [C]//Proceedings of the 20th International Joint Conference on Artificial Intelligence. Hyderabad, India: [s.n.], 2007: 180-185.