形式三角矩阵半环上的双导子

陈艳平， 庄金洪， 谭宜家

(1. 福建商学院信息工程学院， 福建 福州 350012； 2. 福州大学数学与计算机科学学院， 福建 福州 350108)

0 引言

作为模糊代数的推广， 半环理论已在数学的多个领域以及计算机科学、 系统理论分析与信号处理、 自动机理论、 开关理论与控制论、 优化理论等其他学科中有着广泛的应用， 这些学科领域中的许多问题可转化为某类半环上的相关问题[1-2]. 半环上的导子是半环理论中重要研究内容之一[3-5], 应用广泛[1-2, 6-7]. 文献[3]讨论了交换半环上的上三角矩阵代数的 Jordan 导子； 文献[4]研究了半环上某些特殊类型的矩阵半环的导子; 文献[5]讨论了多项式半环的导子.

形式矩阵环是一类非常重要的非交换环， 在有限维代数和算子代数研究中较常见， 是环和模中非对称性质的构造例子和重要反例来源， 也是近期矩阵研究中较活跃的方向之一. 文献[8]证明了非交换素环上的形式三角矩阵环的双导子必是内导子， 推广了文献[9]的结论; 文献[10]又将此结论推广到幺环上的形式三角矩阵代数上; 文献[11]得到了三角代数上满足广义恒等式的导子的结构.

1.2.1.2 患者方面:携带物品较多;文化层次普遍偏低,习惯物品乱堆放;对医院规章制度和病房管理了解甚少,部分病人认为与自己无关。

三角矩阵半环、 形式三角矩阵环都是特殊的形式三角矩阵半环. 本文在上述基础上进一步研究形式三角矩阵半环上的双导子， 探讨加法可消交换半环上形式三角矩阵半环的双导子的基本性质， 及其与两个半环的双导子及双半模同态之间的关系， 从而获得三角矩阵半环双导子的等价刻画.

1 预备知识

定义1[1]设R是一个非空集合， “+”与“·”是R的两个代数运算. 如果以下条件满足:

a) (R, +, 0) 是一个交换幺半群， 其中 0 为R的加法恒等元；

很多中小企业受到传统管理理念的影响，尚未构建科学完善的管理模式，在实际工作中仍然采用传统家族式的管理方法，因此造成对企业财务工作负责的工作人员多数是企业领导者的亲属，专业能力不强，无法结合市场动态变化对财务报告进行完善，也难以针对财务会计工作实施科学化的管理，导致在中小企业的建设和发展过程中，不能发挥出财务会计管理工作的效能，不仅会影响中小企业发展过程中经济效益的获取，甚至会制约和阻碍中小企业在当前市场经济背景下实现持续稳定发展的目标。

c )对任意的a,b,c∈R， 均有a·(b+c)=a·b+a·c， (b+c)·a=b·a+c·a；

d) 对任意的a∈R, 0·a=a·0=0成立；

e) 0≠1.

则称R为一个半环， 记为(R, +, ·, 0, 1) 或简记为R.通常，a·b简记为ab.

一个半环R称为交换的， 如果∀a,b∈R， 均有ab=ba.一个半环R称为非负的， 如果∀a,b∈R由a+b=0 可推出a=b=0.非负半环又称为反环或零和自由半环[1].显然， 任何带有单位元的环都是半环， 每一个布尔代数(包括二元布尔代数)、 模糊代数、 每一个有界分配格以及任何坡都是非负交换半环.另外， 非负实数集对于数的加法与乘法也构成一个非负交换半环.

一个半环R称为加法可消的， 如果∀a,b,c∈R, 由a+c=b+c可推出a=b.半环R中的元素a称为可反的， 如果存在b∈R， 使得a+b=0， 记b=-a， 称b为a的反元.∀c∈R, 定义c-a=c+(-a).易证， 若a是可反元， 则∀c∈R,ac与ca均是可反元且-(ac)=(-a)c， -(ca)=c(-a).若R中所有可反元的全体记作V(R)， 则V(R)非空且是R的一个理想.

定义2[1]半环R上的一个左半模(简称左R-半模)是一个交换幺半群(M, +, 0)， 并且存在一个映射R×M→M， (r,m)→rm， 满足对于任意r,r′∈R,m,m′∈M， 均有：

Ⅰ)r(m+m′)=rm+rm′； Ⅱ) (r+r′)m=rm+r′m；

Ⅲ) (rr′)m=r(r′m)； Ⅳ) 1Rm=m；

(2)网络贷款的现状。根据艾瑞咨询数据统计，2015年我国网络贷款行业的交易金额达到8000亿元，通过网络取得贷款的用户规模达到3970.1万人。在交易结构中，非消费类网络贷款大于消费类网络贷款。

Ⅴ)r0=0=0m.

类似地， 可定义半环S的右S-半模.一个交换半群(M, +, 0)如果既是左R-半模又是右S-半模， 则称其为(R,S)-双半模， 且满足∀r∈R，m∈M，s∈S均有(rm)s=r(ms).在没有特殊指明的情况下，R-半模是指左R-半模.左R-半模(右S-半模)称为忠实的， 如果∀r∈R(∀s∈S)， 当∀m∈M， 均有rm=0(均有ms=0)时，r=0(s=0).(R,S)-双半模M称为忠实的， 如果M既是忠实的左R-半模又是忠实的右S-半模.用V(M)表示半模M中所有可反元的全体， 易证， 若m∈V(M)， 则∀r∈R,s∈S， 均有rm,ms∈V(M)且-(rm)=r(-m)， -(ms)=(-m)s.

定义3设R是一个半环，d：R→R是一个映射且满足对于任意的x,y∈R, 均有d(x+y)=d(x)+d(y).d称为R上的一个导子[1]， 如果d(xy)=d(x)y+xd(y).

定义4设R是半环，d：R×R→R是一个映射且对于任意的x,y,z∈R, 均有d(x+y，z)=d(x,z)+d(y,z),d(x，y+z)=d(x,y)+d(x,z).d称为R上的双导子[9]， 如果d(xy，z)=d(x,z)y+xd(y,z)，d(x，yz)=yd(x,z)+d(x,y)z.

3.2 普通高校的师资力量有待提高，专业的定向运动制图人才需要大量培养，以满足学生对定向运动的专业人才需求。

定义5[9]设R是一个半环，M是左R-半模， 映射f：M→M称为左R-半模同态， 如果对于任意r∈R,m,m′∈M, 均有f(m+m′)=f(m)+f(m′),f(rm)=rf(m).类似可定义半环的右S-半模同态.设M是(R,S)-双半模， 若映射f：M→M既是左R-半模同态又是右S-半模同态， 则称f为(R,S)-双半模同态.

为了进一步提高区县级电视台专题节目的质量，在节目拍摄手段上要下功夫、创新拍摄手段，这样才能够让更多的观众产生新的兴趣点。中央电视台的新闻因具有权威性，所以专题节目用词精准，所表达的意思言简意赅。而区县级的观众从一定程度上来说，观众的文化水平以及专业素质相对较低，在拍摄手段上尽可能以简单直观的方式进行拍摄，这样便于地方观众理解，容易引起观众的共鸣，一定程度上拉近节目与群众之间的距离，吸引观众关注自己的节目。以普法为例，在剧本上以及人物讲述角度上，可以采取第一人称的拍摄手法，语言通俗易懂，镜头简单明了，这样观众就更容易理解和掌握法律知识。

设M是(R,S)-双半模.映射f：M×M→M称为(R,S)-双半模双同态， 如果对于任意的r,r′∈R,s,s′∈S,m,m1,m′∈M, 均有f(m+m1,m′)=f(m,m′)+f(m1,m′),f(m,m1+m′)=f(m,m1)+f(m,m′),f(rms,m′)=rf(m,m′)s,f(m,r′m′s′)=r′f(m,m′)s′.

四是优化综合利用。积极探索政府、合作社、农户3方利益联结机制，大力推广“秸秆全量深翻还田”“秸秆全覆盖免耕还田”“水田秸秆全量还田”“秸秆能源生态”等典型利用模式，因地制宜开展“五化”利用。加大秸秆收购点设置，缩短农户与企业之间的“距离”，减少秸秆田间源头数量。例如，沅江市南嘴镇在7个村设置回收点，安排专人负责收购，效果良好。

定义6[12]设R,S是两个半环，M是一个非零的(R,S)-双半模， 令

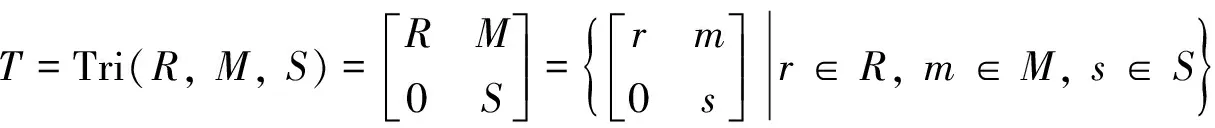
在当前社会中，为了能够促进乡村生态旅游在互联网+背景下得到更好的发展，那么当地的负责部门就可以充分发挥出培训机构的作用，选择合适的培训机构来为乡村生态旅游经营者们提高职业技能培训，并提供相应的平台来让他们互相交流和学习。与此同时，当地政府也可以积极地引进懂得生态旅游经营知识和电子商务的复合型人才，对乡村生态旅游经营者们定期进行网络信息化培训和现场指导，使他们都能够掌握相关的技能。

不难证明，T是一个半环, 称之为形式三角矩阵半环， 也称为半环上的广义三角矩阵半环.若无特别说明， 本研究中T均表示加法可消的形式三角矩阵半环.

2 主要结论

引理1设T=Tri(R,M,S)，d：T×T→T是双导子.则对于任意X,Y,U,V∈T， 均有：

1)p(m)∈V(M)， 并且d(rE11,mE12)=rp(m)E12,d(sE22,mE12)=-p(m)sE12,δ(r,r′)m+r′rp(m)=rr′p(m),mγ(s,s′)+p(m)s′s=p(m)ss′.

ⅱ)d(X,Y)VU+XYd(U,V)=d(X,Y)UV+YXd(U,V).

证明 ⅰ)d(0,X)=d(0·0,X)=0·d(0,X)+d(0,X)·0=0， 同理可证d(X,0)=0；d(I,X)=d(I·I,X)=I·d(I,X)+d(I,X)·I=d(I,X)+d(I,X)， 由半环T的加法可消性， 得d(I,X)=0， 同理可证d(X,I)=0.

ⅱ) 由于d(XU,YV)=Xd(U,YV)+d(X,YV)U=XYd(U,V)+Xd(U,Y)V+Yd(X,V)U+d(X,Y)VU， 同时,d(XU,YV)=Yd(XU,V)+d(XU,Y)V=YXd(U,V)+Yd(X,V)U+Xd(U,Y)V+d(X,Y)UV.于是，XYd(U,V)+Xd(U,Y)V+Yd(X,V)U+d(X,Y)VU=YXd(U,V)+Yd(X,V)U+Xd(U,Y)V+d(X,Y)UV， 由半环T的加法可消性可得:

d(X,Y)VU+XYd(U,V)=d(X,Y)UV+YXd(U,V)

(1)

证明 1) 设d(E11,mE12)=δ(m)E11+p(m)E12+γ(m)E22.利用d(E11,mE12)=d(E112,mE12)=E11d(E11,mE12) +d(E11,mE12)E11及T的加法可消性， 可得:δ(m)=γ(m)=0.于是存在映射p：M→M， 使得:

证明 设d(X,Y)=rE11+mE12+sE22，r∈R,m∈M,s∈S.在式(1)中， 取U=E11,V=m1E12，m1∈M， 利用XY=YX及T的加法可消性， 可得: (rE11+mE12+sE22)(m1E12)=0， 于是,rm1E12=0， 那么,rm1=0.由M是非零忠实的左R-半模， 得r=0.利用式(1)有:d(E11,m2E12)YX+E11(m2E12)d(X,Y)=d(E11,m2E12)XY+(m2E12)E11d(X,Y).利用XY=YX及T的加法可消性， 可得: (m2E12)(rE11+mE12+sE22)=0， 于是,m2sE12=0， 那么,m2s=0.由M是非零忠实的右S-半模， 得:s=0.于是，d(X,Y)=mE12,m∈M.

引理3设T=Tri(R,M,S)， 且M是忠实的(R,S)-双半模，d：T×T→T是一个双导子.则存在m*∈V(M)、R上的双导子δ和S上的双导子γ， ∀r,r′∈R，s,s′∈S， 均有:

a)rr′m*=r′rm*，m*ss′=m*s′s；

b)d(rE11,sE22)=d(sE22,rE11)=-rm*sE12；

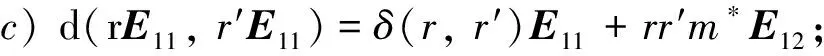
兵团城市的地域性设计策略研究——以十三师红星市中心城区城市设计为例 彭雄亮 姜洪庆2018/01 09

证明 a) 由引理2知， 存在m*∈M， 使得:d(E11,E11)=m*E12.由引理1中 ⅰ)可知，d(E22,E22)+d(E11,E22)=0，d(E11,E22)+d(E11,E11)=0， 所以m*∈V(M).再由T的加法可消性知，d(E22,E22)=d(E11,E11)=m*E12.再利用引理1 中ⅰ)可得:d(E11,E22)=d(E22,E11)=-m*E12.

⑨ ㉘ ㉜ Caronline Rogus，“Fighting the Establishment:The Need for Procedural Reform of Our Paternity Laws”，Michigan Journal of Gender＆ Law，67(21)，2014，p．79，p．98，pp．114 ～115．

b) 由于(rE11)(E22)=(E22)(rE11)=0， 由引理2知， 存在m1∈M， 使得:d(rE11，E22)=m1E12.于是，d(rE11，E22)=d((rE11)E11，E22)=(rE11)d(E11，E22)+d(rE11，E22)E11=(rE11)(-m*E12)+(m1E12)E11=r(-m*E12)=-rm*E12.由于 (rE11)(sE22)=(sE22)(rE11)=0， 由引理2知， 存在m2∈M， 使得:d(rE11，sE22)=m2E12.于是,d(rE11，sE22)=d(rE11，E22(sE22))=E22(m2E12)+(-rm*E12)(sE22)=-rm*sE12.

同理可证，d(sE22,rE11)=-rm*sE12.

(2)

下证δ：R×R→R是R上的双导子.

d) 类似于c)可证.

引理4设T=Tri(R,M,S)， 且M是忠实的(R,S)-双半模，d：T×T→T是双导子.则存在(R,S)-双半模同态p：M→M和q：M→M， ∀r,r′∈R,s,s′∈S,m∈M， 均有:

引理2设T=Tri(R,M,S)， 且M是忠实的(R,S)-双半模，d：T×T→T是双导子.若X,Y∈T满足XY=YX， 则存在m∈M， 使得d(X,Y)=mE12.

d(E11,mE12)=p(m)E12

(3)

由引理1中 ⅰ)知,p(m)∈V(M)， 且d(E22,mE12)=-p(m)E12.现设d(rE11,mE12)=δ(r,m)E11+p(r,m)E12+γ(r,m)E22.由rE11=(rE11)E11及式(3)， 可得:d(rE11,mE12)=(rE11)d(E11,mE12)+d(rE11,mE12)E11=rp(m)E12+δ(r,m)E11.又由mE12=(mE12)E22及引理3 中b)， 可得 :

本课程主要采取项目教学的方法和一体化教学的方式。以任务驱动、项目引领型课程为主体结构，按照实际工作任务、工作过程和工作情境来组织课程。从岗位需求出发，尽早让学生进入工作实践。以工作任务为中心来整合相应的知识和技能，实现理论与实践的统一，为学生提供体验完整工作过程的学习机会，从而改变以前电工电子的系统教学框架，使知识结构、技能要求、教学内容弹性化。教学过程主要在实验实训室完成，让学生边学边做，在学中做、做中学，将动手动脑紧密结合，相得益彰，即完成了一体化教学。

d(rE11,mE12)=d(rE11,mE12)E22+(mE12)d(rE11,E22)=rp(m)E12

(4)

类似可证d(sE22,mE12)=-p(m)sE12.下证， 映射p：M→M是(R,S)-双半模同态.

类似可证，ξ(m,m′)ss′=ξ(m,m′)s′s.

克氏综合征又称曲细精管发育不全症，其基本临床特征为：不同程度男性性成熟障碍、小睾丸、无精子症、青春期明显乳房发育、高促性腺激素水平[3]。生殖细胞减数分裂过程中染色体不分离导致性染色体二体生殖子产生，是本病的遗传病理机制[4]。此病在婴幼儿期不易发现异常，青春发育期睾丸小才被发现，出现某些女性体征才会引起注意，但大部分患者因婚后不育到医院就诊才能确诊。绝大多数的患者射出的外周精液中是没有精子的，但极个别报道精液中偶见精子[5]。本例患者不但精液中有精子，而且妻子自然受孕生育1胎，实为罕见。其原因可能是其中一条X染色体处于失活状态，但具体机制有待进一步研究。

2)类似于1)可证.

b) (R, ·, 1) 是一个幺半群， 其中 1 为R的乘法恒等元；

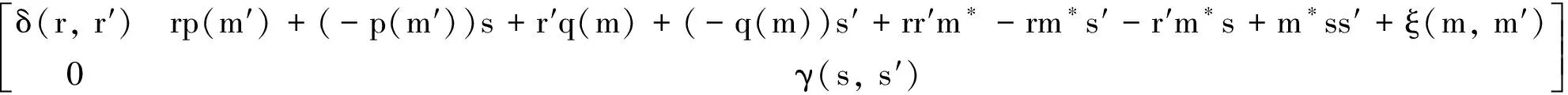
① 对于任意m∈M,p(m),q(m)∈V(M)；

② ∀r,r′∈R,s,s′∈S,m,m′∈M， 均有：

δ(r,r′)m′+r′rp(m′)=rr′p(m′),m′γ(s,s′)+p(m′)s′s=p(m′)ss′

δ(r,r′)m+rr′q(m)=r′rq(m),mγ(s,s′)+q(m)ss′=q(m)s′s
rr′ξ(m,m′)=r′rξ(m,m′),ξ(m,m′)ss′=ξ(m,m′)s′s.

证明 充分性： 通过直接计算可知d是T的双导子.下证必要性.

由引理4～5， 可得①～②. 证毕.

SF用它的经营理念更快帮助客户、对市场更快更好地做出反应：为了提高企业的市场竞争力不断地推出新产品，使服务周期能够缩短；调整竞争策略，使经营成本能够降低。SF为国民经济的持续健康发展贡献了税收做出了积极贡献，它的企业规模也在缓解社会就业压力上做出了应有的积极贡献。

经计算， 可知d：T×T→T是双导子.

经超声检查后，本组60例患者均明确诊断，诊断符合率100%，其中慢性阑尾炎急性发作7例、阑尾周围脓肿6例、急性化脓性阑尾炎14例、急性单纯性阑尾炎26例，急性坏疽穿孔性阑尾炎7例、。其中阑尾腔有粪石者11例。见表。

3 结论

本研究分析了形式三角矩阵半环双导子. 探讨了加法可消交换半环上形式三角矩阵半环Tri(R,M,S)的双导子的基本性质及判定方法， 给出了形式三角矩阵半环 Tri(R,M,S)的双导子与两个半环R与S的双导子及(R,S)-双半模同态之间的关系， 从而获得了三角矩阵半环双导子的等价刻画.