马尔可夫调制的双分数布朗运动环境下重置期权的定价

陆恬依

(南京财经大学 应用数学学院，江苏 南京 210023)

0 引言

随着经济的发展和人们生活水平的提高，人们开始拥有越来越多的资金用于投资，由此衍生出种种不同的期权定价模型.朱盛等[1]通过对金融市场的上大量实证分析证实了股票价格会受到过去价格的影响，利用偏微分方程得到了几何布朗运动环境下重置期权价格的数值解.董盈盈等[2]在假定股票价格满足分数布朗运动驱动的随机微分方程的条件下，得到了在分数布朗运动环境下重置期权的定价.张学莲等[3]在上述模型的基础上，给出了双分数布朗运动环境下重置期权的定价模型及公式.现在已经有更多的学者参与到双分数布朗运动的应用研究中来，研究了不同种类的期权定价问题[4-11].考虑到在实际金融市场上无风险利率、股票波动率等变量是随着时间变化的随机变量，1973年美国经济学家Black和Scholes通过假设股价概率服从正态分布，并假设其股价的走势服从马尔可夫链，利用随机微分方程推导出期权定价模型，从而得到了微分方程的解[12].同年，Merton和Scholes在《政治经济学杂志》上提出假定无风险利率并非常数[13]，而是随着时间变化的随机变量，从而建立了期权定价模型，减少了原有B-S模型的假设条件，使其更符合实际经济情况.宋瑞丽[14]、王伟[15]将现有的(双)分数布朗运动模型置于马尔可夫调制下，利用无套利定价的方法，分别计算出具有固定敲定价格的亚式看涨、看跌期权的定价公式.刘雪汝[16]研究了风险资产式由两因素马尔可夫调制的随机波动过程和两因素马尔可夫跳扩散随机波动过程驱动，对欧式期权和美式期权进行了定价估计,并求出了美式看跌期权关于欧式看跌期权和早期执行溢价的分解结果[17].目前，有关重置期权的定价方式有很多种，比如鞅方法、偏微分方程方法、蒙特卡洛方法、保险精算方法[18]等，其中保险精算方法[19]由Mogens Bladt于1998年首次提出，以范围广、操作便捷著称.

本文在前人研究的基础上，建立马尔可夫调制的双分数布朗运动模型，运用连续时间的马尔可夫链来描述不同经济周期中的不同状态，再利用保险精算方法得到符合实际金融市场的定价公式.将重置期权定价模型进一步推广.

1 模型假设

在金融市场中，市场的利率变化、股票平均回报率和股票的波动率随时发生变化，因此，其时间状态可以由连续时间的马尔可夫链{Xt}描述，状态空间可表示为X：=(X1,X2,…,XN)，那么{Xt}t∈Γ只取有限个值(e1,e2,…,eN)，其中ei=(0,…,1,…,0)∈R，其中市场利率r(t)，股票平均回报率μ(t)和股票波动率σ(t)可分别表示为

r(t)=,r=(r1,r2,…,rN)∈RN，

μ(t)=<μ,Xt>,μ=(μ1,μ2,…,μN)∈RN，

σ(t)=<σ,Xt>,σ=(σ1,σ2,…,σN)∈RN.

且〈·,·〉表示内积，内积的值会因马尔可夫链{Xt}t∈Γ状态变化而变化.

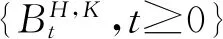
假设股票价格{St,t≥0}满足方程

(1)

引理1[3]随机微分方程(1)的解为

对于任意的随机方程，由于r(t)=,μ(t)=<μ,Xt>,σ(t)=<σ,Xt>均为随机变量，则可定义在时间t∈(0,T)，可得

(2)

定义2 股票价格{St,t≥0}在[t,T]上的期望回报率为β(u),u∈[t,T]定义为

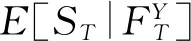
引理2 股票价格{St,t≥0}在[t,T]上的期望回报率为

β(s)=μ(s),s∈[t,T].

证明由引理1可知

则

故

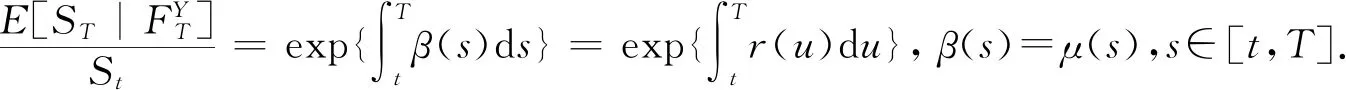
定义3 用保险精算方法将c(Y,T)，p(Y,T)定义为看作是看涨期权与看跌期权在t时刻的资产价值，其中Y为执行价格，T为到期日，表示如下：

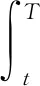
2 马尔可夫调制的双分数布朗运动环境下重置期权的定价

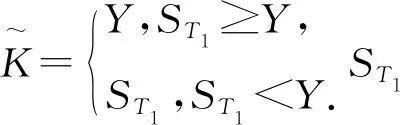
定理1 双分数布朗运动环境下，到期日为T，执行价格为Y的欧式看涨期权在时刻t的保险精算定价为

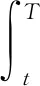
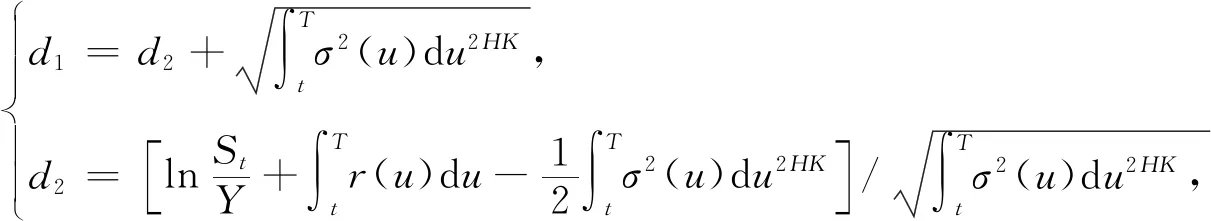
其中N(·)为一元标准正态分布函数.

证明因为

和

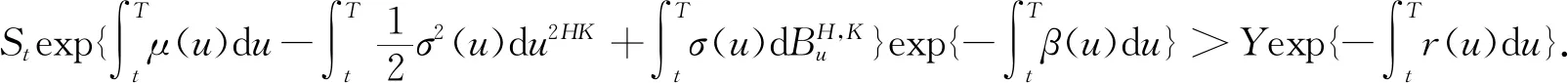
又因为

β(s)=μ(s),s∈[t,T].

记

经化简得

由于

则

故

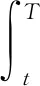
1)当0≤T1≤t时，即t∈[T1,T]时，C(t,T1,T)=C(t,T,Y)IST1≥Y+C(t,T,ST1)IST1≤Y；

2)当t≤T1≤T，即t∈[0,T1]时，

证明1)当0≤T1≤t时，即t∈[T1,T]时，由欧式期权的定价公式易得结论;2)当t≤T1≤T，即t∈[0,T1]时，先假设

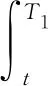
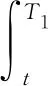
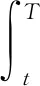
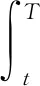
则

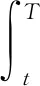
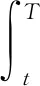
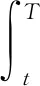
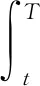
I1-I2+I3-I4.

先计算I1,由于

经化简得

则

再计算I2

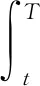
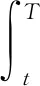
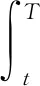
然后计算I3.由于

经化简得

则

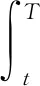
通过等量代换,得

代入上述积分得

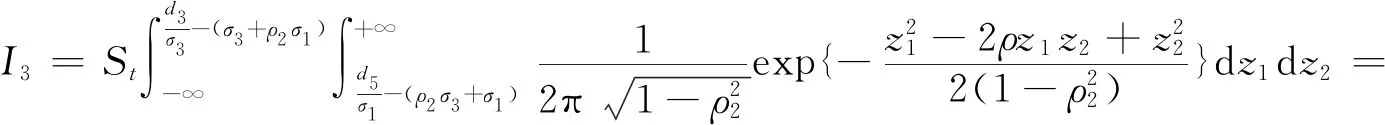
最后计算I4

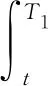
合并上述计算式可得定理2.

注1 1)当K=1时，可得马尔可夫调制的分数布朗运动环境下重置期权的定价公式；2)当T1=T时，可得马尔可夫调制的双分数布朗运动环境下标准欧式看涨期权的保险精算定价公式.

推论1 马尔可夫调制的双分数布朗运动环境下标准欧式看跌期权的保险精算定价公式：

(a)当t∈[T1,T]时，P(t,T1,T)=P(t,T,Y)IST1≤Y+P(t,T,ST1)IST1>Y；

(b)当t∈[0,T1]时，

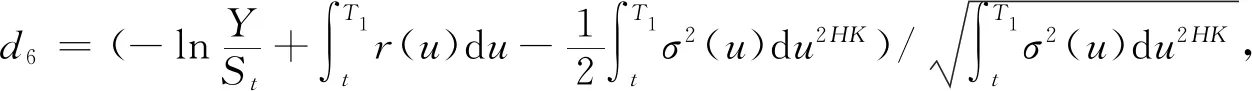
3 数值算例

为便于分析引入连续时间的马尔可夫链对双分数布朗运动模型下重置期权的影响，选取双分数布朗运动环境下欧式重置看涨期权为例，假设存在一只股票S1，在t=0时刻S1(0)=35，指数H=0.55，K=0.65，并假设金融市场的经济状态只有两个状态e1、e2，当经济状态处于e1时，市场利率r1=0.04，股票波动率σ1=0.4；当经济状态处于e2时，市场利率r2=0.03，股票波动率σ2=0.3，同时，假定马尔可夫链的转移概率矩阵为

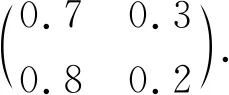
假设t=0时，初始状态为e1，执行价格K为45到65，步长为5，借助Matlab蒙特卡洛模拟10 000次，分别得到以下双分数布朗运动模型环境下欧式看涨重置期权价格和马尔可夫调制的双分数布朗运动模型下欧式看涨重置期权价格.

注2C1表示双分数布朗运动模型下欧式重置看涨期权价格；C2表示马尔可夫调制的双分数布朗运动模型下欧式看涨重置期权价格.

由表1和图1可知双分数布朗运动模型下得到的期权价格比马尔可夫调制的双分数布朗运动模型下得到的期权价格大.由此可见，如果在实际金融市场中不考虑状态会发生变化这一现实情况，将会严重高估期权的价格.

表1 两种不同模型下欧式看涨重置期权数值结果

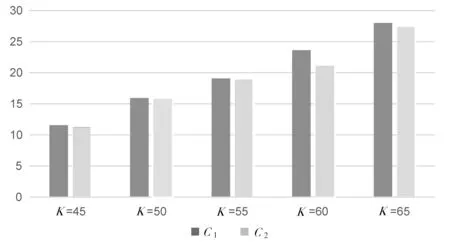
图1 两种不同模型下欧式看涨重置期权数值结果比较

4 结论