含过程噪声Wiener系统的递推两阶段参数估计
景绍学
(淮阴师范学院 物理与电子电气工程学院,江苏 淮安 223300)
0 引言
近年来,非线性系统的辨识与控制引起了研究人员的广泛关注.模块化非线性系统是非线性系统的一种类型,因结构简单、实用性强,在非线性系统建模中获得了广泛应用[1].Wiener系统是一种典型的模块化非线性系统,由一个线性动态模块后面串联一个非线性静态模块组成的.目前,Wiener系统已经成功应用于许多的工业过程建模中,如pH值中和过程、热交换器、蒸馏塔等[2-3].
Wiener系统的辨识问题引起了系统辨识研究人员的持续关注,大量的研究成果得以发表.其中主要的算法包括:Pawlak等[4]在非参数辨识方面提出一种两部算法,先用非线性最小二乘估计线性模块的脉冲响应函数,基于得到的线性参数用非参数核回归得到非线性模块的参数估计值;Bai[5]提出了一种非参数方法用于确定辨识线性环节参数所需的最少的非线性先验知识;Michalkiewicz[6]基于改进的神经网络算法对一类Wiener系统进行了辨识;Tang等[7]先用一系列幅值不等的阶跃信号激励Wiener系统以获得非线性模块的结构形式,然后基于粒子群优化算法对一类Wiener系统的参数进行了辨识;Duwaish等[8]基于遗传算法对一类Wiener系统的参数辨识问题进行了研究;对于时变参数Wiener系统,Kobayashi等[9]在不需要估计中间变量的情况下,基于一种神经网络结构对一类Wiener系统进行了辨识.Nordsjo等[10]运用EKF算法将Wiener系统的辨识问题转换为带不等约束的非线性优化问题,并提出了一种CEKF算法;在Wiener系统的频域辨识方面,Giri等[11]针对由非参数线性模块和间隙非线性模块构成的Wiener系统,运用正弦激励提出了一种频域辨识算法,可以得到参数的一致估计;非线性形式的表达方面,研究人员也提出了相应的方案,如:Totterman等[12]利用支持向量机回归辨识非线性模块,Kozek等[13]用最优局部线性模型表达分段线性表示的非线性函数,Voros[14]用多段线性表示非线性模块;在收敛性分析方面,Hu等[15]给出了一种针对递推辨识算法的强收敛性结果,Li等[16]分析了一种定点迭代算法的收敛性.
然而,Wiener系统的辨识问题远未得到解决.目前存在的主要难点有:
1)在模型结构已知的情况下,大多数辨识算法首先参数化系统,然后利用传统的算法辨识含有参数乘积项的过参数系统,随后再进行参数的分离工作以得到待辨识的单个参数向量.由于含参数乘积项,导致待辨识参数向量的维数较高,算法的计算量较大,辨识代价较高,实时性较差.
2)相当一部分算法在辨识时没有考虑全噪声的问题,或仅考虑了输出噪声的影响,对于工业上存在的过程噪声下的Wiener系统的辨识问题,相关文献较少.
为解决上述问题,本文提出一种含过程噪声Wiener系统的递推两阶段参数估计算法.主要内容包括:用有限脉冲响应函数和一种多项式函数分别表达系统的动态环节的传递函数和静态环节的反函数;提出一种两阶段算法以消除过程噪声的影响;基于递推思想以减小算法的计算量.
1 问题描述
考虑离散非线性Wiener系统(图1).图1中u(k)和y(k)分别为系统的输入、输出信号,v(k)为均值为零的高斯白噪声信号.其中,噪声v(k)作用在线性子模块和非线性子模块的中间,即该噪声为过程噪声.B(z-1)为线性动态子模块的传递函数,N(x2(k))为非线性静态函数.x1(k)和x2(k)为不可测中间变量.过程噪声v(k)在较大程度上增加了辨识的难度.

图1 过程噪声扰动的Wiener系统
系统的线性动态传递函数可用一个阶次为nb的有限脉冲响应函数表示,即:
(1)
其中
θb=[b1,b2,…,bnb]T∈nb×1,φb(k)=[u(k-1),u(k-2),…,u(k-nb)]T∈nb×1
(2)
为了描述连续非线性静态函数,多项式函数被广泛采用.图1中非线性函数N(x2(k))的反函数可用如下的阶次为nβ的多项式逼近:
(3)
其中
θβ=[β1,β2,…,βnβ]T∈nβ×1,φβ(k)=[y(k),y2(k),…,ynβ(k)]T∈nβ×1
(4)
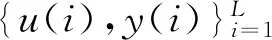
2 递推两阶段参数估计算法
对于过程噪声扰动的Wiener系统,考虑式(1),有
(5)
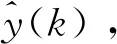

(6)
(7)
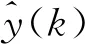
(8)
不失一般性,令式(8)中β1=1,由式(7)和(8)得
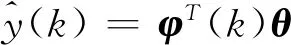
(9)
其中
(10)
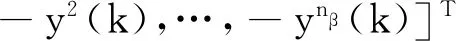
(11)
定义并最小化如下的准则函数
(12)
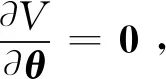
(13)
将式(12)改写成二次型的形式
(14)
其中
(15)

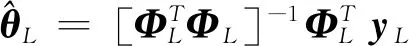
(16)
对于式(16)给出的参数估计值
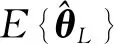
(17)
由于式(11)和式(15)中的信息向量φ(k)中包含了受噪声v(k)污染的系统输出y(k),导致式(17)中的等式右边第二项中Φ中包含噪声项,因此式(16)给出的最小二乘估计是有偏估计.
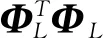
(18)
为此,可采用辅助变量法[17].根据辅助变量的选取规则,选择由上述最小二乘估计计算出的线性动态模块的输出估计值作为辅助变量.即:
(19)
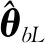
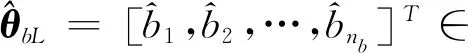
(20)
(21)
于是,式(16)变为
(22)
其中
(23)
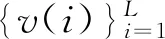
(24)
其中θ0表示参数的真实值.
证明在式(22)的两边同时取数学期望,当L→∞时
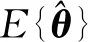
(25)
为减小计算量,推导算法的递推形式.将式(22)改写成
(26)
定义
(27)
由于
(28)
由式(26)可得
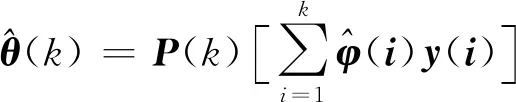
(29)
则
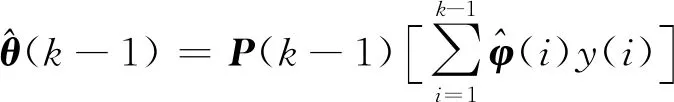
(30)
在式(30)两边同乘以P-1(k-1)
(31)
考虑到式(27)和(31)和,式(29)变为

(32)
令
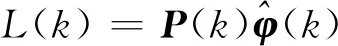
(33)
式(32)可写成
(34)
进一步把P(k)改成递推形式,由式(28)
(35)
运用矩阵求逆公式,得
(36)
将式(36)代入式(33)得
(37)
综合式(34),(36)和(37)得到基于辅助变量的参数估计递推公式如下:
(38)
至此,所提估计算法的步骤归纳如下:
Step1:设置辨识初值
Step2:收集输入、输出数据u(k)和y(k);
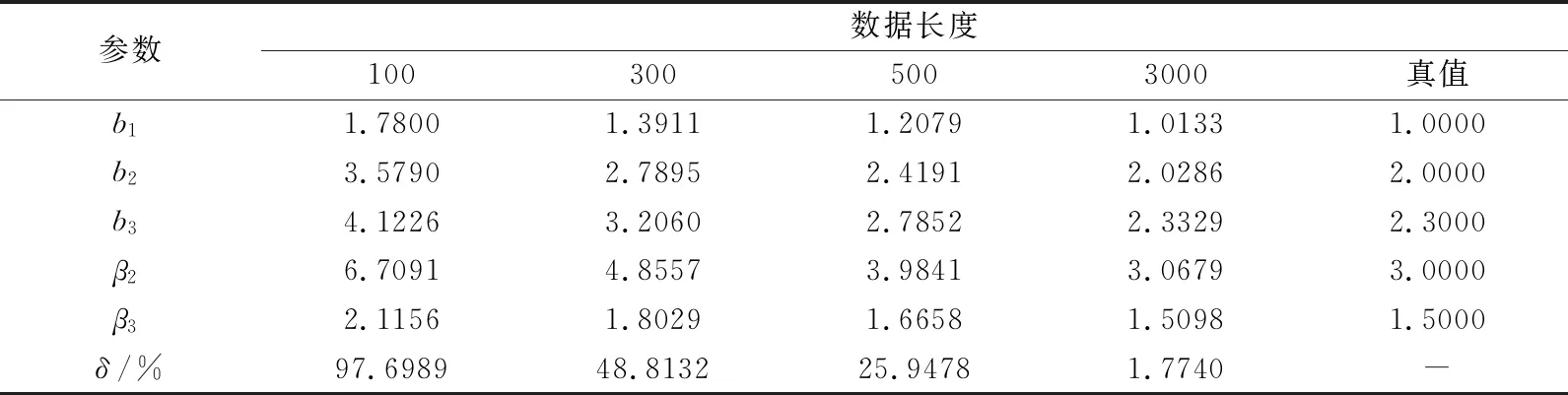
Step6:令k=k+1,如果k 由于算法在参数估计时分Step3和Step7两个阶段递推进行,因此所提的算法被称为递推两阶段估计算法(recursive 2-stage algorithm,R2S).与此相对应,两个阶段均采用一次完成算法的辨识算法被称为一次完成两阶段算法(One-shot 2-stage algorithm,O2S). 所提算法的计算复杂度如表1所示.由于一般情况下n远小于L,所以所提的递推算法R2S的计算量远小于一次完成算法O2S,仿真例的运行时间也证实了该结论. 表1 R2S和O2S算法比较 考虑图1所示的Wiener系统,可得: (39) 其中,输入幅值在[1,2]之间且服从均匀分布,噪声为零均值高斯白噪声. 所提算法R2S对算例的辨识结果如表2所示,参数估计误差随数据长度变化情况如图3所示,其中噪声方差为0.012.从表2和图3中可以看出,随着辨识的进行,估计误差逐渐减小并趋于稳定,当数据长度为3 000时,估计误差为1.77%,表明所提算法具有较高的辨识精度. 表2 R2S算法辨识结果 作为比较,O2S算法的参数估计误差如表3所示.不难看出,在数据长度和噪声水平相同的情况下,递推算法和一次完成算法的估计误差相差较小,说明两种算法的精度基本一致,而所提递推算法的计算量远小于传统O2S算法. 表3 不同噪声水平下R2S和O2S估计误差 为了显示所提算法的优越性,用单阶段RLS算法对仿真例进行了辨识,参数估计误差如图2中虚线所示,图中实线为R2S算法的估计误差曲线.对比两条曲线不难看出,在同等条件下,所提算法的估计误差要远小于对比的RLS算法,印证了单阶段RLS算法给出的参数是有偏的. 图2 R2S与RLS算法估计误差 图3 不同噪声水平下R2S算法估计误差 运用所提算法,在不同噪声水平下对所给仿真例进行了辨识,图3显示了所提算法在不同噪声水平下的估计误差曲线. 从图3中可以看出: 1)随着辨识数据的增加,3种噪声水平下估计误差均有下降,表明不同噪声水平下估计误差均随辨识数据的长度的增长而减小; 2)在辨识的初始阶段,3条曲线参数估计值均出现了较大的波动,随着辨识的进行,参数估计误差逐渐稳定,表明所提算法能给出较稳定的参数估计值; 3)随着噪声水平的提高,曲线波动的幅度变大,表明噪声对辨识的影响在增加,并且最终的估计误差也在变大,说明噪声水平的升高导致辨识精度变差,估计误差与噪声水平呈正相关. 为了辨识一类过程噪声扰动的Wiener系统的参数,在用FIR函数和多项式分别逼近待辨识Wiener的线性动态传递函数和非线性反函数的基础上,提出了一种递推两阶段参数估计算法.在参数化系统的基础上,分别使用最小二乘算法和辅助变量法进行参数辨识,得到参数的无偏估计.在进行参数估计时,为了减小算法的计算量,两个阶段均采用了递推算法.数值仿真表明所提算法是有效的.
3 算法验证
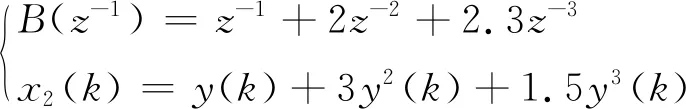

3.1 R2S与O2S的辨识结果比较

3.2 R2S算法与RLS算法的辨识结果比较

3.3 不同噪声水平R2S算法的辨识结果比较
4 结束语

