对数伽玛分布变点模型的估计

程贝丽,周菊玲

(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)

0 引言

对数伽玛分布是一种重要的寿命分布,广泛应用在生物学、金融及新型农村合作医疗住院费用等可靠性领域[1-4].由于对数伽玛分布具有向右偏斜的特点,所以在非寿险精算中也得到了一定的应用.Zhang等[1]从生物学角度研究了对数伽玛分布的模型;Amini等[5]研究了对数伽玛分布族的性质;王成元等[6-8]研究了不同损失函数下对数伽玛分布尺度参数的贝叶斯估计,并对不同的贝叶斯估计做出比较;金秀岩[9-10]分别探讨了对数伽玛分布和负对数伽玛分布条件概率的封闭性、Pearson-χ2距离和渐进性;熊福生[11]研究了对数伽玛分布和负对数伽玛分布的再生性,得到了一些与再生性、准再生性相关的结果.在近几年的研究中,变点问题一直是统计学中的热点问题.变点问题一般的研究方法有最小二乘法、贝叶斯方法、极大似然方法、累次计数法和非参数法.陈希孺[12]结合概率变点问题,介绍了极大似然音乐方法、累计次数法和贝叶斯方法;黄月兰[13]分别用极大似然方法、贝叶斯方法和最小二乘法讨论了单参数指数分布的变点问题.沙雪云等[14]用极大似然方法和贝叶斯方法讨论了单参数Parato分布的变点问题;陈杰[15]分别在非贝叶斯场景下和贝叶斯场景下对变点进行检测.但是，用不同的方法研究对数伽玛分布变点问题的文章还比较少，本文用极大似然估计和贝叶斯估计研究单变点对数伽玛分布的参数估计问题.

1 对数伽玛分布单变点模型

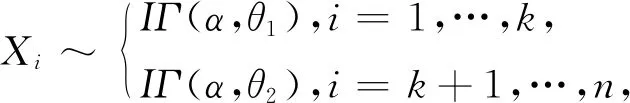
下面分别用极大似然估计方法和贝叶斯估计方法对单变点对数伽玛分布的参数进行估计.

2 对数伽玛分布的极大似然估计

设随机变量X1,X2,…,Xn为来自对数伽玛分布模型中的一个样本,则对其n个独立观测值x1,x2,…,xn得到的似然函数为

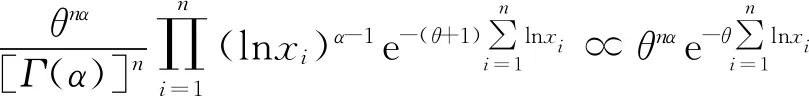
(1)

令γ=(θ1,θ2,k),则单变点对数伽玛分布的似然函数为

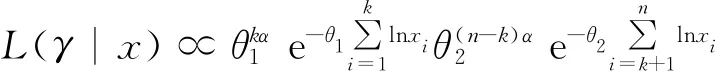
(2)

固定k,对θ1,θ2求极大,得

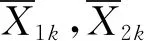
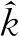
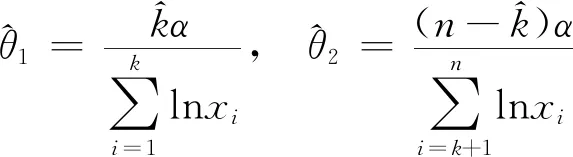
(3)

3 对数伽玛分布的贝叶斯估计

在统计推断中,样本的状态固然重要,但历史的经验也同样举足轻重.故为了提高统计推断的质量,应注意先验信息对整个统计推断的影响,没有先验分布或取不恰当的先验分布都可能使统计推断的结果产生误差.

首先确定各参数的先验分布:

1)变点k的先验分布为无信息先验分布:π(k)∝1；

2)尺度参数θ1,θ2的先验分布分别取无信息先验分布和共轭先验分布.

讨论尺度参数θ1,θ2的先验分布取无信息分布时参数的贝叶斯估计,假定θ1,θ2,k之间相互独立.

引理1 设随机变量X服从对数伽玛分布,参数θi的先验分布π(θi)为无信息先验分布,X1,X2,…,Xn为服从对数伽玛分布的一个样本,记X=(X1,X2,…,Xn),T=(t1,t2),则θi的后验分布服从Ga(nα,T).

证由式(2)可知,x1,x2,…,xn是样本X1,X2,…,Xn的n个独立观测值的似然函数,又已知参数θi的先验分布为无信息先验分布,即π(θi)∝1.则参数θi的后验概率密度函数为

于是θi|x～Ga(nα,ti),故θi|X～Ga(nα,T).

则当参数θi的先验分布为无信息先验分布时,对数伽玛分布单变点模型的似然函数为

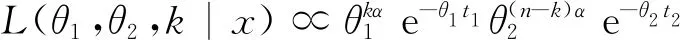
(4)

得到各参数的满条件分布如下：

讨论尺度参数θ1,θ2的共轭先验分布为伽玛分布时参数的贝叶斯估计,假定θ1,θ2,k之间相互独立.

引理2[3]设随机变量X服从对数伽玛分布,参数θi的先验分布π(θi)为伽玛分布Ga(ai,bi),X1,X2,…,Xn是服从对数伽玛分布的一个样本,记X=(X1,X2,…,Xn),T=(t1,t2),则θi的后验分布服从Ga(nα+ai,T+bi).

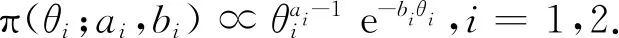
则参数θi的后验概率密度函数为

于是θi|x～Ga(nα+ai,bi+ti),故θi|X～Ga(nα+ai,bi+T).

则当θi的先验分布为伽玛分布时,对数伽玛分布单变点模型的似然函数为

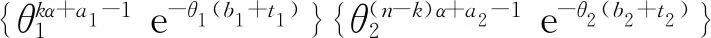
(5)

得到各参数的满条件分布如下：

尺度参数θ1,θ2满条件分布的形式较为简单,可直接用Gibbs抽样,而变点k的满条件分布较为复杂,不再适合Gibbs抽样方法,则利用MH算法进行抽样.

MCMC算法可分为如下几个具体步骤.

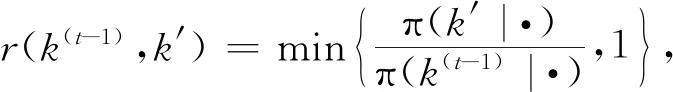
为了确保抽样的收敛性,在模拟过程中,先进行10 000次的预迭代,再进行20 000次的Gibbs迭代,即从10 001次开始到30 000次结束.假设Gibbs样本的容量为M,如果第B次以后逐渐收敛,则把后M-B个样本的均值作为各未知参数的估计值.

4 随机模拟

4.1 极大似然估计

根据对数伽玛分布的概率密度函数和极大似然估计式(3),利用MATLAB软件对未知参数θ1,θ2,k进行估计,结果如表1所示.

表1 参数θ1,θ2,k的极大似然估计

模拟结果显示,极大似然方法能够估计未知参数的值,但参数θ1,θ2,k的极大似然估计值与真值相差较大,精度不高.

4.2 贝叶斯估计

取超参数ai=bi=1,i=1,2,取B=10 000,M=30 000,根据各参数的满条件分布进行MCMC模拟,将20 000个样本的均值作为各未知参数的估计值.

1)当先验分布取无信息先验分布时,参数θ1,θ2,k的参数估计如表2所示.

表2 无信息先验分布情况下参数θ1,θ2,k的参数估计

2)当先验分布取共轭先验分布时，参数θ1,θ2,k的参数估计如表3所示.

表3 共轭先验分布情况下参数θ1,θ2,k的参数估计

图1、图3是变点k抽样迭代图,是判断Gibbs样本是否收敛的重要依据.用MCMC方法模拟时,会同时产生两条迭代链,若这两条迭代链逐渐稳定并趋于重合,则说明Gibbs抽样是收敛的,变点k的两条迭代链如图2、图4所示.

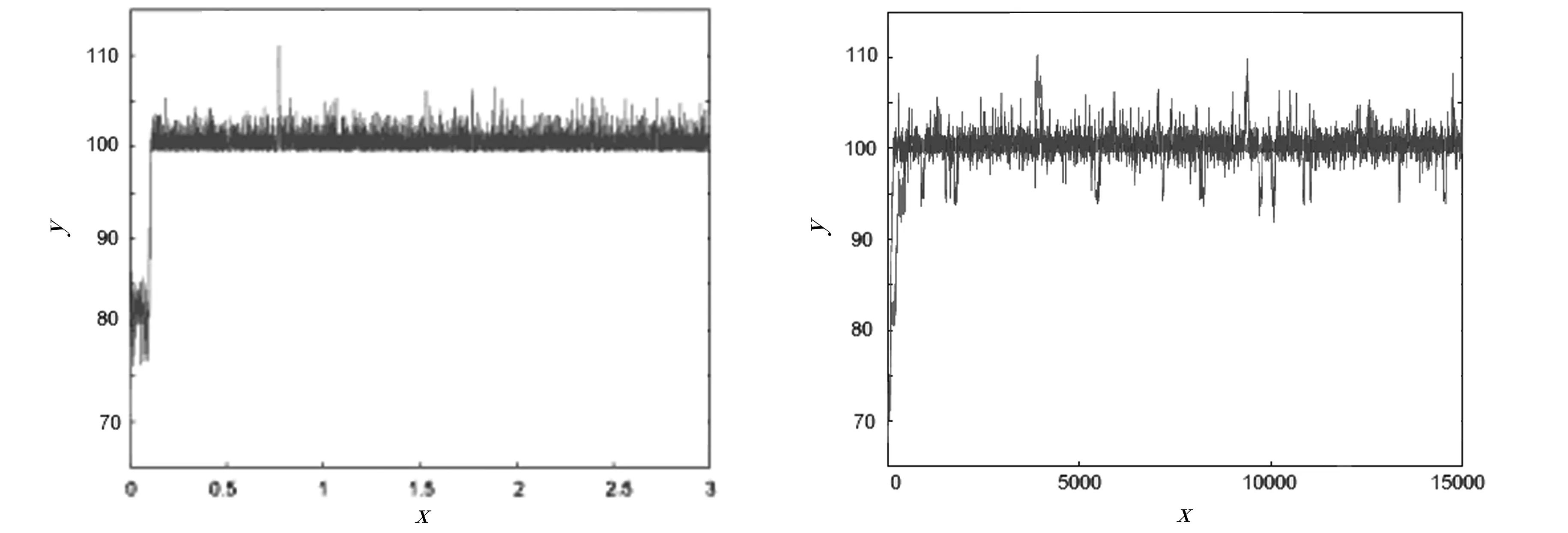
图1 变点k的抽样迭代图 图2 变点k的两条迭代链

图3 变点k的抽样迭代图 图4 变点k的两条迭代链

下面对模拟的结果进行分析,从表1、表2中可以看到θ1,θ2,k这3个参数的均值与真值都较为接近,且MC误差都小于2%,即各参数的贝叶斯估计精度较高;各参数的标准差也比较小,说明数据比较稳定;各参数置信水平0.95的区间[2.5%分位数,97.%分位数]的长度也较短,即得到的区间估计效果较好.由图1和图3可以看出Gibbs抽样基本在变点附近波动,呈现出一定的规律性.其次,观察图2和图4,可以发现产生的两条马尔科夫链稳定且趋于重合,说明收敛性较好.综上所述,对数伽玛分布变点问题可以用MCMC方法实现,且在不同先验分布下,估计值的精度不同.

5 总结

本文主要研究对数伽玛分布尺度参数存在变点时的参数估计问题.随机模拟的结果表明:两种方法都能够有效地对未知参数进行估计.在相同条件下,贝叶斯估计所需要的时间远远大于极大似然估计,但是相比于极大似然估计,贝叶斯估计的值更稳定,也更接近真实值.通过比较可知,共轭先验分布下的贝叶斯估计值优于无信息先验下的贝叶斯估计值.这说明了选取恰当的先验分布可以提高统计推断的质量.因此,基于本文中单变点对数伽玛分布的模型,先验分布取共轭先验分布时,未知参数的贝叶斯估计是最优的.