辅助函数法和Cole-Hope变换法求STO方程的精确解
张 静
(南京财经大学 应用数学学院,江苏 南京 210023)
0 引言
非线性偏微分方程广泛应用于应用数学和物理学的各个分支,尤其在流体力学、高分子物理学、固体物理学等领域应用广泛.Sharma-Tasso-Olver(简称STO)方程最初由Sharma和Tasso在研究Burgers方程族时提出[1-2],目前已有不少学者对其进行了深入研究.杨立娟等[3]利用推广的Hirota双线性方法研究了(1+1)维STO方程的新精确解,并进一步讨论其局域孤子结构.Dai等[4]使用了修正的简单方程法对STO方程精确解以及Hirota-SatsumaKdV系统进行阐述.Zhang等[5]着重分析了STO方程的对称约化及精确解.此外,学者们通过G′/G2展开法[6]、Auto-Bäcklund变换法[7]、exp-函数法[8-9]同样获得STO方程新的精确解.最近,杨健等[10]提出了辅助函数法,借助此方法获得了许多非线性偏微分方程的精确解.李伟[11]借助Cole-Hope变换获得了(2+1)维Burgers方程和Kdv方程的n-孤子解.
受以上研究启发,本文主要研究如下Sharma-Tasso-Olver(简称STO)方程
(1)
其中u=u(x,t),α为任意常数.
接下来,借助辅助函数法和Cole-Hope变换法方法来构造STO方程的精确解.
1 辅助函数法
对于方程(1),作行波变换,
u(x,t)=u(ξ),ξ=kx-ct
(2)
其中k、c是非零常数.
将式(2)代入式(1),有
-cu′+3αk2(u′)2+3αku2u′+3αk2uu″+αk3u‴=0
(3)
假设方程(3)有如下形式的精确解
(4)
其中ai为待定系数,而幂级数的最高次幂n可通过平衡常微分方程的非线性项和最高阶导数项来确定.
f(ξ)满足如下辅助常微分方程
f(ξ)′=f(ξ)2+λf(ξ)+μ
(5)
对辅助方程(5)的λ、μ分情况讨论,并求解该方程可以得到f(ξ)的7组不同精确解[10-12].
由方程(3)中的u2u′和u‴,得到n=1,则方程(1)的解可以表示为
u(ξ)=a0+a1f(ξ)
(6)
将式(5)和式(6)代入式(3),合并f(ξ)的同次幂项系数,得到非线性代数方程组
(7)
求解式(7)得到两组解分别如下:
情形1:
(8)
其中a0、k为任意常数.
将式(8)代入式(6)中可得到STO方程的形式解
u(x,t)=a0-kf(ξ)
(9)
再将f(ξ)的7组不同精确解分别代入式(9),可获得方程(1)的如下7组解:
①当λ=0,μ=0时,有

②当λ=0,μ>0时,有
③当λ=0,μ<0时,有

④当λ≠0,μ=0时,有
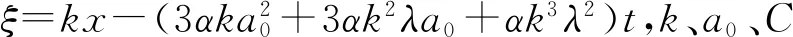
⑤当λ≠0,μ≠0,λ2-4μ>0时,有
⑥当λ≠0,μ≠0,λ2-4μ<0时,有

⑦当λ≠0,μ≠0,λ2-4μ=0时,有

情形2:
(10)
其中k为任意常数.
将式(10)代入式(6)中可得到STO方程的形式解,
u(x,t)=-λk-2kf(ξ)
(11)
再将f(ξ)的7组不同精确解分别代入式(11),同样可获得方程(1)的如下7组解:
①当λ=0,μ=0时,有
其中ξ=kx,k、C为任意常数.
②当λ=0,μ>0时,有
③当λ=0,μ<0时,有
其中ξ=kx+4αk3μt,k、C为任意常数.
④当λ≠0,μ=0时,有
其中ξ=kx-αk3λ2t,k、C为任意常数.
⑤当λ≠0,μ≠0,λ2-4μ>0时,有
⑥当λ≠0,μ≠0,λ2-4μ<0时,有
其中ξ=kx-(αk3λ2-4αk3μ)t,k、C为任意常数.
⑦当λ≠0,μ≠0,λ2-4μ=0时,有
其中ξ=kx,k、C为任意常数.
2 Cole-Hope变换法
设
u=k(lnf(x,t))x
(12)
其中k为待定常数.
本文只解决k=1时的情形,后续对于k的不同取值可以进一步研究.下面将式(12)代入方程(1)并化简可得
(fxt+αfxxxx)f-(fxft+αfxfxxx)=0
(13)
将式(13)两边同时除以f2,得
(14)
对式(14)积分,并令积分常数为零,得
ft+αfxxx=0
(15)
若f为式(15)的解,则通过式(12)即得到方程(1)的解.
设f(x,t)=px3+rt为式(15)的拟解,并代入式(15)得r=-6αp,所以式(15)有如下形式的解,
f(x,t)=p(x3-6αt)
(16)
这里p为任意常数.将式(16)代入式(12),得
(17)
式(17)即为方程(1)的新的精确解.
对于式(13),也可令
(18)
考虑其孤子解,可设
f=1+eθ,θ=p1x+r1t
(19)
将式(19)代入式(18),得
(20)
其中p1为任意常数.
将式(19)和式(20)代入式(12),可获得方程(1)的单孤子解为
在上面得到的两组解中,取系数为一些确定的值,可以得到具体的结构,利用mathematica画图,结果如图1和图2所示.
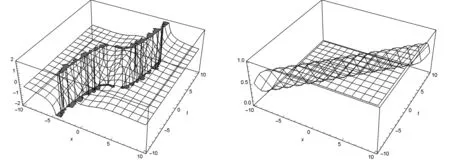
图1 α=1时的精确解 图2 α=1,p1=1时的单孤子解
3 结束语
本文通过行波变换、齐次平衡原理,运用辅助函数法求出了STO方程的7组行波解,利用Cole-Hope变换法对k=1的情况进行研究得到了方程新的精确解和单孤子解,后续对k的不同取值,有待进一步研究.两类方法也可用于求解其他具有类似性态的非线性偏微分方程.

