玩转轴对称，感受数学之美

施琦

【摘 要】《轴对称图形》是苏教版数学三年级上册第六单元的内容，重点是掌握辨别轴对称图形的方法。本文在梳理教材的基础上对教材进行再加工、再整合，学生通过“认”“辨”“做”“赏”四个环节，丰富对轴对称图形的体验。

【关键词】轴对称图形 对称轴 对称美

本节课初步教学对称现象和轴对称图形。新版教材一共分五步呈现：

（1）仔细观察，感知对称。

（2）启发思考，找出特征。

（3）抽象图形，引导发现。

（4）尝试探索，描述特征。

（5）动手操作，丰富体验。

教材的编写紧扣学生生活实际，精心挑选了学生熟悉且感兴趣的材料，例1让学生观察体会图形中的对称现象，学生对于对称现象已经不陌生，甚至很多人在幼儿园时期就已经会对折之后剪出对称的图形。因此，学生能够初步感知生活中这些物体都是对称的。接着通过“对折”这一活动，引导学生初步认识轴对称图形的基本特征。然后例4通过剪松树的图形，以及用折、画、剪等方法做出不同的轴对称图形，进一步积累感性认识，丰富对轴对称图形的体验。

基于对教材的理解以及对学生已有认知经验的了解，学生虽然不知道什么是“轴对称图形”，但是部分学生对于“对称”两个字，已经有了初步的感知。出示一些生活中的图片，学生通过观察能够一眼看出其中的对称现象，同时有少部分学生甚至有过剪纸经验，已经能独立做出一些图案。

轴对称图形给人的感觉是美的，因此设计本节课时，笔者就想着能否让学生在学习的过程中感受到数学课也可以是很美的。同时这节课注重学生的体验，因此在教学设计时，笔者通过几个具体的活动来丰富学生的操作体验，通过“认”“辨”“做”“赏”四个环节丰富学生的认知体验。

一、丰富素材，感知生活中的对称之美

【片段一】  “认”轴对称图形

师（导入）：同学们，昨天是西方的一个节日，知道是什么节吗？瞧，施老师把圣诞老爷爷请到我们课堂上来和我们一起上课。再过几天就是我们中国的传统节日了，知道是什么节吗？

生：春节。

师：是的，春节到了，家家户户都要贴上美丽的窗花做装饰。

师：瞧，圣诞老人给我们带来了我国古老的民间艺术——剪纸。让我们一起来欣赏吧。

数学课程标准指出，“教师要积极开发、利用各种教学资源，为学生提供丰富多彩的学习素材”。基于此，这一段的导入设计，笔者从学生的生活实际出发，再结合本课的上课时间正好是圣诞节前后，于是以这样一个场景导入教学，同时作为PPT的背景，为后面让学生寻找生活中的对称提供素材。同时为了弘扬我国的优秀传统文化，在课始引入我国传统的剪纸艺术，通过上下对称和左右对称两种对称现象，引导学生初步感知生活中的对称。

二、抽象感知，体会模型中的对称之美

【片段二】“认”对称轴

师（提问）：瞧，圣诞老爷爷还给我们带来了蝴蝶、北京天坛和飞机模型。这些图形还是对称的吗？

生：通过对折才能判断。

师：这个方法不错，在小组里试一试吧——有什么发现？

生：对折以后一模一样。

师：什么是一模一样？

生：重合得没有一点缝隙。

师（小结）：我们把像这样对折之后两边能够完全重合的图形叫作轴对称图形。

师（提问）：那么，轴对称图形的“轴”在哪呢？请你来指一指。

师（小结）：是呀，这条折痕就是轴对称图形的“轴”，一般我们用点画线表示。

这部分内容是本节课的教学重点，轴对称图形的判断标准就是“轴”，学生通过思考以及结合已有的认知经验，得出可以通过对折来判断的结论，但是学生不能充分地理解“完全重合”，只能用自己的语言说出“一模一样”“没有一点点多余”这样类似的描述，这时就需要教师及时将“完全重合”的意义在学生理解的基础上加以解释，通过对学生嘴里说出来的词语加以总结，更能加深学生对知识的理解，从而顺势揭示出“轴对称图形”的含义。

三、操作体验，感受图形中的对称之美

【片段三】“辨”轴对称图形

师（谈话）：同学们，通过刚才的研究我们认识了一个新朋友——轴对称图形，圣诞老爷爷还给我们带来了一些老朋友，这几个图形是轴对称图形吗？

师（要求）：先观察，在学习单的这个位置填上自己的猜想。

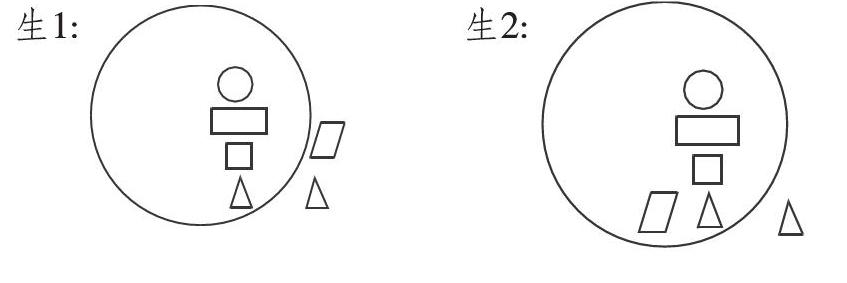
师：老师这有一组放大后的图形，形状相同，大小不同，请把你认为的轴对称图形放到圆圈里，不是的放到圆圈外面。

生1：                                         生2：

师：出现了两种声音。俗话说“实践出真知”，大家在小组里想办法验证一下吧。

师（明确）：看来我们判断一个图形是否是轴对称图形，关键是看这个图形对折后能否完全重合。

在这一环节的教学中，让学生先通过肉眼判断，請不同想法的学生到黑板上呈现自己的猜想，再通过对折的方式验证以前学过的图形中哪些是轴对称图形、哪些不是轴对称图形。在这一过程中，有学生对于长方形、正方形、圆形有不同的折法验证，笔者请用不同方法的学生加以示范，为之后找出图形中有几条对称轴的学习埋下伏笔。数学课程标准明确指出，要“感悟数学思想，积累数学活动经验”，让学生通过将轴对称图形移进“大圆”里，也是渗透了数学中的集合思想。

四、动手设计，创造图形中的对称之美

【片段四】“做”轴对称图形

材料准备：各种大小、颜色不同的彩纸。

师（谈话）：学会了认识、辨别轴对称图形，你想自己做一个轴对称图形吗？你想做什么？

生：我想做一棵松树。

师（追问）：能说说你想怎样做吗？

生：先对折，再在纸上将画好的松树的一半剪下来。

师（小结）：原来我们要想做出一个轴对称图形，我们只需要对折纸，再画出其中的一半，然后沿着边剪下来就可以了。赶紧试试吧！

在这一环节中，笔者为学生提供了足够多的纸张，给予他们足够多的时间进行创作，在同学相互引导和启发下，学生几乎都能做出一些简易的轴对称图形。在学生的创作过程中，笔者挑选其中一部分充实本节课的板书，把学生心中的对称现象做成具体的对称图形，通过图像表征丰富学生的认知。学生都争前恐后地想要展示自己的作品，对于班级同学的作品，笔者在班级黑板报上留了一块位置专门展示学生的作品，落实了数学课程标准中“关注学生情感态度发展”的目标。

五、学会欣赏，享受生活中的对称之美

【片段五】“赏”轴对称图形

师：刚刚我们用双手创造出了美丽的事物，生活中还有哪些轴对称图形呢？对称是一种创造作品的重要方法，也是自然界中常见的一种现象。

师（谈话）：古今中外的许多著名建筑也是对称的，对称使得它们看起来更加雄伟、壮观。自然界中也有许多对称的现象。对称不仅是为了美观，还有一定的科学道理。蝴蝶、蜻蜓等昆虫能在空中自由地飞行，是因为它们都有一对或几对对称的翅膀。

师（小结）：掌握对称的奥秘，不仅可以帮助我们发现感受自然界的美妙与和谐，还能使我们获得一些有趣的数学知识。

通过前面的学习，学生已经对轴对称图形有了初步的认识，也能尝试自己做出简单的轴对称图形，这一环节主要结合课本中“你知道吗”的内容，结合古今中外建筑中的对称以及自然界中的对称现象，引导学生体会数学与生活之间的联系，感受数学的价值，从而愿意学、喜欢学。

注：本文为南京市教育科学“十三五”规划课题（L/2018/246）“图像表征支持儿童数学学习的实践研究”的研究成果。