PDSA视域下基于教师学习的中学数学课例研修研究
伍春兰
PDSA视域下基于教师学习的中学数学课例研修研究
伍春兰
(北京教育学院数学系,北京 100120)
针对培训中数学教师参与“课例研究”不足的现状,构建了两轮PDSA课例研究框架,并在几个中学数学教师长期培训项目中开展行动研究.结合因式分解的课例研究,阐释了主要研究过程及效果.研究结论:依托两轮PDSA研究框架,及提炼的教学设计“六三”对话支架,助力了数学教师基于课例的学习与研究,达成了在大单元背景下,以学生、教师及编者的角色,从知识技能、数学思考、问题解决和情感态度4个维度将数学教学内容激活,实现了数学学术形态教学内容向教育形态的深层转化.
教师学习;课例研究;课例研修;因式分解
1 问题提出
近几年,中共中央、国务院颁布了一系列有关教师教育的文件,确定了按照“四有好老师”的标准,建设“高素质专业化创新型”教师队伍的愿景,并对教师培训做出指示.《关于全面深化新时代教师队伍建设改革的意见》提出了“改进培训内容,紧密结合教育教学一线实际,组织高质量培训,使教师静心钻研教学,切实提升教学水平”的培训要求[1].《中国教育现代化2035》指明了“夯实教师专业发展体系,推动教师终身学习和专业自主发展”的培养路径[2].《关于深化教育教学改革全面提高义务教育质量的意见》揭示了培训切入点“强化课堂主阵地作用,切实提高课堂教学质量”[3].“课例研究”是以课堂教学为载体的教师参与的一种研修活动,许多学者的研究[4-7]表明“课例研究”可助推教师专业发展,特别是学科教学知识丰盈的有效途径.因此,“课例研究”作为一种研修手段,体现了上述文件的精神.
在研究者承担的若干中学数学教师培训需求和满意度调研,数据都显示“课例研究”是参训数学教师首选的研修方式,这一统计结果在实际培训的相关活动中也得到印证.尽管“课例研究”在培训中广受青睐,但许多培训项目受限于某些主客观因素,仅把“课例研究”简单地视作一次课例观摩活动,对“课例”的前期分析及后期的互动交流不足,针对性的专业提升缺位,教学改进的行为难觅等.按照Kirkpatrick的培训效果四层次评估(反应、学习、行动、效果)模型[8],这样的“课例研究”止步于学了什么(第二层次),忽略了参训者实际教学中态度或行为改变(第三层次)及学校整体教学质量提升(第四层次)的跟进.已发表的相关成果和文献综述[9-10]显示,已有研究集中在“课例研究”概念的辨析,已有模式的介绍、评析及应用,而从教师学习的视角基于学科的教学改进的研究不足.近十多年,中小学教师培训转向教师学习已成趋势[11-13],“研训一体”也成常态[14],这就意味着教师培训理应遵循教师学习的内在机制,从教师学习的需求出发,强化沉浸式现场教学与研究.PDSA(Plan-Do-Study-Act)是改善工作质量的行动框架,其间还包括3个基本问题[15]:要完成什么改善?怎么知道变化是一种进步?能做出什么改变来改善?
正是在上述背景下,研究者提出了PDSA视域下基于教师学习的中学数学课例研修研究.
2 研究框架
该课题中的课例研修,是以“课例研究”为中介的研修,即由专家与一线教师构建的学习共同体,在前期课例研磨的基础上,从教育现场出发,通过展示、表达和对话,实现沟通交流,达成共识,再经过实践反思,内化成教师的个体信念和知识的循环渐进过程.
2.1 指导:社会建构主义学习观和观察学习论
社会建构主义认为学习不仅是学习者以自己原有的知识经验为基础完成的个人认知活动,更主张学习是一个社会文化互动过程,即学习者借助一定的文化支持,参与某个共同体的实践活动,内化有关知识的意义建构过程[16].
班杜拉(Bandura)的观察学习,就是在一定情境中观察榜样的行为及其结果,获得新行为的象征性表象.所谓榜样就是观察学习过程中观察学习的对象,其本质就在于示知新行为的途径,引导学习者做出与之相应的行为.观察学习包含4个密切相关的心理活动过程:注意、保持、复制和动机[17].
研究者以社会建构主义学习观和班杜拉的观察学习论为指导,主张教师学习要在一个专业发展社群中,通过榜样示范引发落差,促进教师反思及教学改进.
2.2 依据:PDSA循环理论
PDSA循环理论源自Walter A. Shewhart,1950年美国质量管理专家戴明(Deming W. Edwards)将此循环简化为PDCA(Plan-Do-Check-Act),20世纪90年代又提出了PDSA循环结构.PDSA建立在一个组织持续不断完善和研究的假设之上,其循环是不断发现问题和解决问题的过程,同时每一个循环体内环环相扣,即上一环节是下一环节的依据,下一环节又是上一环节的落实和具体化[18].
PDSA/PDCA在国内外各领域得到广泛应用,但在国内教师培训层面上还未引起普遍关注.Stigler和Hiebert认为课例研究可以从PDSA的范式中获益[19],Catherine Lewis阐述了课例研究的PDSA的应用和展望[20],韩笑等学者也指出PDSA在教育改进实践中值得推广和应用[21].该研究构建并实施了两轮PDSA循环结构,以期达成Kirkpatrick四层次评估模型的第三和第四层次的培训效益.
2.3 借鉴:课例研究典例
作为术语的“课例研究”,兴起于20世纪五六十年代日本的“授业研究”(jugyoukenkyuu),其研究步骤可概括为提出问题、制定计划、上课观课、研讨反思、修改计划[22].香港的“课堂学习研究”(learning study)以“变易理论”(variation theory)为框架,基于课堂教学的行动研究.上海的“行动教育”(action education)是以课例为载体的“三阶段两反思”的教师教育模式,即在原行为、新设计、新行为的3个阶段间有两轮反思与调整[23].
上述3个“课例研究”的典例,虽然名称相异,模式也有差别,但本质上都指向如何改进课堂教学、提高教师专业水平,其流程基本都暗合PDSA的行动框架.
2.4 建构:研究框架
在社会建构主义学习观和观察学习论指导下,借鉴3个“课例研究”的典例,以及一些职后教师培训模式[24-45],构建了课例研修的两轮PDSA研究框架,并赋予了PDSA新内涵.
第一轮PDSA指向教学范例的打磨,引发教学改进之念.(1)计划P:聚焦研究问题;选择执教者和课题;设计教师和学生问卷或访谈提纲.(2)实施D:教学设计;教师和学生问卷或访谈.(3)研究S:初始课的研磨.(4)行动A:教学设计修改完善.
以教学设计的基本理论为纲,在实践中提炼出教学设计的“六三”对话支架(表1),其中“六”指6个维度,包括标准、文献、教材、学生、同伴或专家及自己;“三”指每个维度的3个视角.

表1 教学设计的“六三”对话支架
凭借前测或访谈,达成与学生的对话;通过磨课和交流,实现与同伴或专家的对话;依托教学设计的修改完善,完成与自己的对话.
第二轮PDSA旨在教学反思的深入,推动教学改进之举.(1)计划P:确定观察要点及观察量表.(2)实施D:教学范例观察.(3)研究S:教学范例研讨.(4)行动A:教学反思及改进.
当学员进入范例执教者的课堂,个体观察与合作观察同步.个体观察,即以同课异构的心态带着问题观摩:如果是我,怎样上这节课;有哪些借鉴;有哪些困惑;有哪些建议.合作观察,即依照团队的研究主题分工合作地观察.
研究者认为课堂教学并存着两个主体及其共同活动:教师以学习的组织者、引导者与合作者的身份主导教学,学生以学习的主体身份学习发展,而师生的每个活动又以问题情境为中介.问题情境要围绕目标展开,关注社会生活、其它学科和数学,能激发学生学习动机.学生的3个参与(行为、认知、情感)因需而定,以调动认知特别是思维参与为主,兼顾情感和行为参与.教师在课堂教学中不越位、缺位,以合宜的教学策略追求教育价值的最大化.为此研究者开发了“三三”课堂观察量表(表2).第一个“三”指3个维度(问题情境、学生学习和教师教学),第二个“三”指每个维度的3个视角,并对细目做了约定.观察记录以课堂环节为单位,团队研讨后再给出各环节和整节课的观察结论.

表2 课堂环节观察量表
与教学范例对比研究中发现“落差”,即从教学设计、教学实施、课堂观察、说课议课的过程中,发现自己与同伴、专家在观念、实操及细节等的差距,以确定改进的方向和策略.将反思具体化,一是撰写反思,明确改进方向;二是鼓励行动研究,改进教学.
3 实践案例
以因式分解的课例研究,阐释主要研修过程.
3.1 调研分析
采用焦点团体访谈法,就因式分解教学,分别对北京市3个区县共计36名初中数学教师(基本情况见表3)做了开放性问题的调研,得到下面4点结论.

表3 教师基本情况统计(%)
(1)教师能关注到因式分解对学习分式、二次根式、一元二次方程、二次函数等的作用,但系统设计的意识不够,缺少全面规划.比如,在学习初始阶段会让学生做一些超过学生现有水平的题目,挫伤了学生的学习积极性.又如,在后续学习中需要用到因式分解时,没有创设学习进阶的机会,反而抱怨学生的“无能”.其实,因式分解是贯穿中学代数的一个重要内容,因为它是代数式的计算、化简、求值及论证4类问题中恒等变形的重要手段之一,也是思维品质培养的极佳载体.因此,从数学学科和学生学习的逻辑,因式分解的学习理应螺旋上升、不断深化,一蹴而就的心态不可取.
(2)教师有单元设计的理念,但习惯于遵从现行教材顺序,每节新授课仅学习一种分解方法.由于教学内容单一,缺乏一定的挑战,教学方式又以教师主导为主,学生虽然学时轻松,思维却没有得到相应的锻炼,综合分解技能还需再加课时训练.认知负荷理论表明[46],学习者处理加工相宜难度的高交互性学习材料时,会促进思维发展和能力提升.因此适度提高相关认知负荷,如增强学生的自主学习活动,或整合单元学习内容,可提高认知效率并发展智能.
(3)教师知道数与式的类比,整式乘法与因式分解的对比,不同分解方法的概括与选择,思想方法的运用(特殊与一般、局部与整体、转化与化归等)及思维品质的培养中能体现因式分解教学的价值,但教师仅是表层地类比、对比、概括、选择、运用和培养.比如,仅由整数分解为几个因数的积的形式,类比整式得出因式分解概念,而忽视分解的目的、分解的作用的类比.事实上,通过对整数分解为几个质数积的目的(了解数的结构)、作用(化简、巧算等)的提升,不仅易推得因式分解的目的、作用,从而增强学习的内在动机,也为各因式要分解到不能再分为止(隐性知识)找到理据.
(4)教师反映的学生问题及原因主要有:①态度上轻视,一是认为因式分解简单,二是不清楚为什么要学习;②做题易错,一是负迁移影响,二是分解不彻底;③学习效果持续不长,一是理解肤浅,二是螺旋上升的机会错失.
3.2 发现落差
针对因式分解教学的主要问题:学生思维参与不足,每节课的认知负荷不及,研究者的设计和实施主要有两点
改善.
3.2.1 前测利用

研究者设计了前测(表4),不仅了解了学生学习的现状,也成为教学引入的切入点.
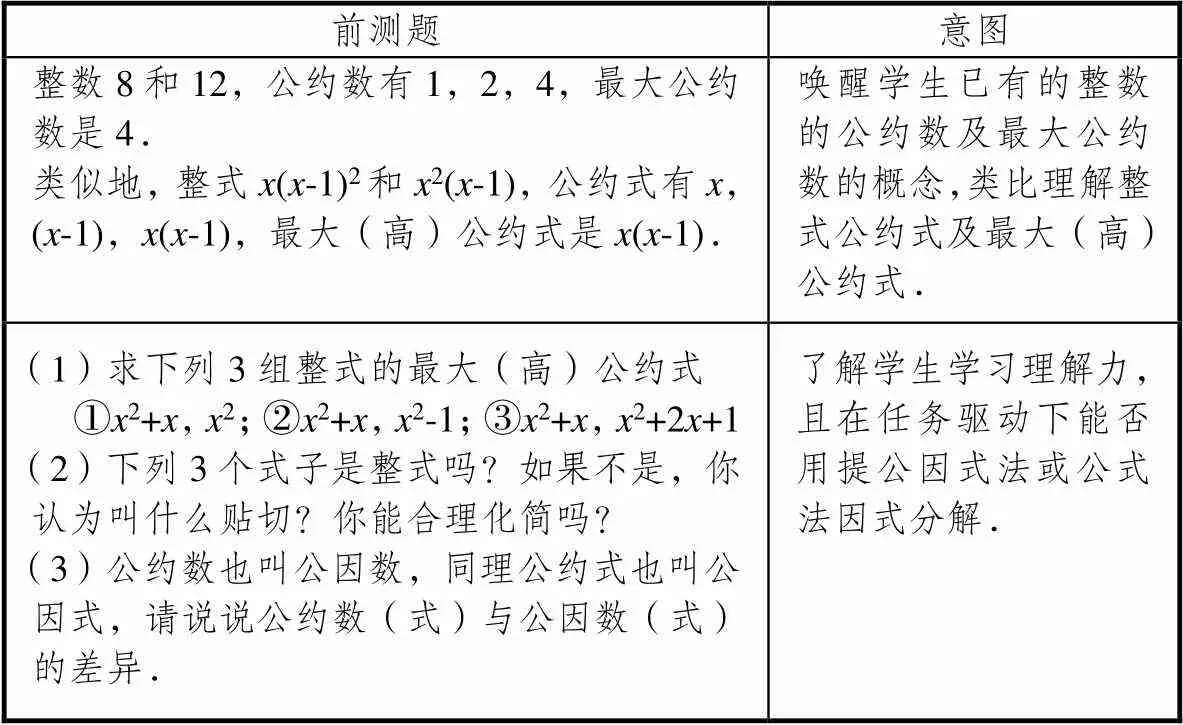
表4 前测题
尽管整式除法、分式概念学生还没有学习,但由前测的题(1),以及分数的性质,多数学生能顺畅合理地解决前测的题(2),至于算理暂且“难得糊涂”,待到分式学习时再去深究.这样的设计既为分式的学习埋下了伏笔,也为因式分解的学习注入了意义,同时初步感受了因式分解的基本方法——提公因式法和公式法.
3.2.2 单元重构
按照符合学生思维规律的“整体—部分—整体”的原则,设计两个改进方案,单元课时计划见表5.方案1提供了更多挑战任务,强调学生思维品质的培养.比如,公式法教学时,不仅从算理、乘法公式、几何意义上理解(第一节课),而且在第二节课复习时,让学生从分组分解法上再认公式:
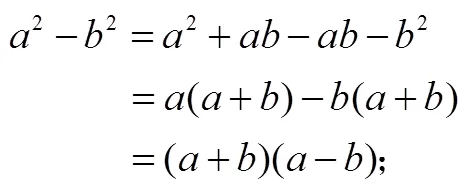
再认有机地勾联了分组分解、提取公因式和公式法,点燃了学习兴趣,开阔了认识视野.方案2学习公式法时,创设了学生以公式(平方差和完全平方)自主编制因式分解题目的思维活动,并用对比方式学习平方差公式法和完全平方公式法,激活了学习热情,突破了学习难点.

表5 单元课时计划
3.3 教学改进
学员甲,在北京市生源较好的某校任教,教龄12年.看到多数学生对前测问题(表4)基本能应用因式分解得到正确答案,特别是观摩了教学范例,促使她有了教学改进的动力,选择了方案1实施.她发现与过往教学比较,学生学习的积极性明显提升,他们更愿意思考,布置的找题、编题及做题(有关因式分解)的作业完成的质量很高;学习相同内容原来需要4课时,现在3课时就够了,而且学生的思维参与活动还增加了.同时她还感受到了远期效益,比如分式的计算、化简,以及解方程等问题中,多数学生能主动应用因式分解求解.这次教学改进经历,也影响了她后面的教学.
学员乙,在北京市生源一般的某校任教,教龄19年.因式分解教学,她一直是按照教材编写顺序线性展开.观摩了教学范例后受到触动,于是做了一个对比实验研究:对比班保持原来的设计教学,实验班选择了方案2.分别在3节课后、学完因式分解一周后做了后测(4个题目),解题正确率见表6.
学员乙所任教的两个班,学生学业水平基本相当,而且她还是对比班的班主任.两次后测的统计结果令她吃惊,也坚定了她不断学习、研究,单元设计改进教学的信念.
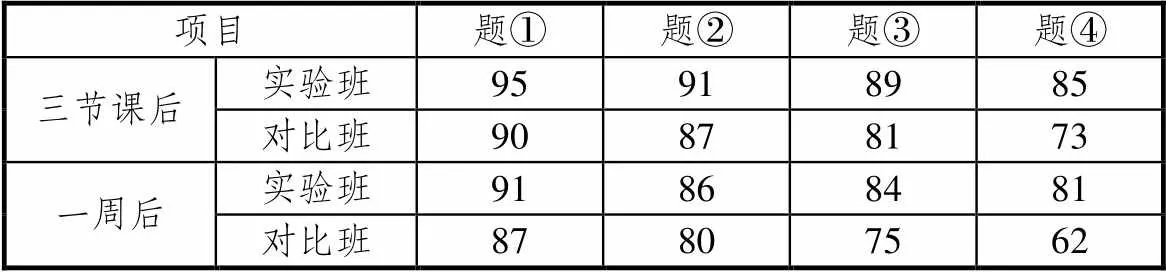
表6 两次后测正确率(%)
4 研究结论
近几年,研究者在几个中学数学教师长期培训项目中建立了专家为首席,基于教师学习的课例研修共同体.依托两轮PDSA研究框架,引导共同体的教师在教学范例的观察中发现“落差”,激发学习.教学范例背后反映出的数学学科统领性观念,以及特定学习内容学生理解和误解的知识、组织架构的知识和教学策略知识[47],经过学习共同体的互动研讨,逐渐获得群体认同,提升了教师对相关内容的数学本质的深度理解,推动了教师从数学学科核心素养的培养和单元系统设计的视角,对自我教学的审视与改进.每次教学设计和实施的改进都记录了蕴含其中的变化,这些变化使教师感受到自己的进步,体验到学习研究的乐趣,也彰显出课例研修的价值.
4.1 “六三”对话开启教师学习之旅
以往的教学设计,教师更多依赖教参和下载的他人设计,缺少自己的主张,自主学习、研究的意识不足.“六三”支架通过与标准、文献、教材、学生、同伴或专家及自己的对话,助力了教师学习与研究,达成了在大单元的背景下,以学生、教师及编者的角色,从知识技能、数学思考、问题解决和情感态度4个维度将数学教学内容激活,实现了数学学术形态教学内容向教育形态的深层转化.
4.2 教学范例刺激教师学习之需
在学习共同体内,发现“落差”是教师学习的前提,也是教学改进的动力,因为相仿的教学对象、日常的教学内容、创意的教学设计会刺激教师学习之需.因此,作为教学范例的课例,选取于数学课程标准所规定的核心内容,或学生数学学习的难点内容,亦或数学教育价值体现不足的内容.教学范例的执教者,需遴选有学习研究意识、善于表达的成员.通过与自己和他人(同伴或专家)多次反复研磨,以期能吸引观摩学员的注意并易于互动,从而产生认同感和学习心理与行为.
4.3 教学改进落实教师学习之效
教师研修的核心目标除了激发教师学习的动机,还应促使教师教学行为的变化[48].根据嬗变学习理论,教师学习的目标不仅是学科教学知识的累积,而且是教师的理念、角色、气质等多方面的实质性变化,以及由教师的发展所带动的学生的成长[49].因此,基于教师学习的课例研修的显性目标是课堂教学改进,隐性目标是实践智慧形成.当然,教师通过学习实现嬗变,需要经历一个复杂的过程,其中专业引领与自主反思及成员之间相互影响,相互促进的社会认同至关重要.
[1] 新华社.中共中央国务院关于全面深化新时代教师队伍建设改革的意见[EB/OL].(2018-01-31)[2021-03-01].http://www.gov.cn/zhengce/2018-01/31/content_5262659.htm.
[2] 新华社.中共中央国务院印发《中国教育现代化2035》[EB/OL].(2019-02-23)[2021-03-01].http://www.gov. cn/xinwen/2019-02/23/content_5367987.htm.
[3] 新华社.中共中央国务院关于深化教育教学改革全面提高义务教育质量的意见[EB/OL].(2019-07-08)[2021-03-01].http://www.gov.cn/zhengce/2019-07/08/content_5407361.htm.
[4] 顾泠沅,王洁.教师在教育行动中成长——以课例为载体的教师教育模式研究[J].全球教育展望,2003,32(1):44-49.
[5] 郑毓信.“问题意识”与数学教师的专业成长[J].数学教育学报,2017,26(5):1-5,92.
[6] 陈蓓.课例研究与教师数学学科教学知识(MPCK)的发展[J].数学教育学报,2016,25(4):74-78.
[7] 肖春梅.课例研究:数学教师学科教学知识发展的有效途径[J].教学与管理,2015(18):100-103.
[8] 赵德成,杜屏,杜育红.参与式教学培训效果:基于四层次评估模式的分析[J].教师教育研究,2009,21(6):47-52.
[9] 张虹,何宇恒,朱惠莲.国内外课例研究述评(2009—2019)——现状与展望[J].中国外语,2020,17(3):55-62.
[10] 王允,黄秦安.中国数学教师继续教育的发展轨迹与动态趋势——基于《数学教育学报》(1992—2018年)的文献计量与内容分析[J].数学教育学报,2020,29(1):81-85,97.
[11] 陈霞.以教师学习为中心的教师培训课程重构路向[J].教育发展研究,2017,37(18):58-64.
[12] 郑文芳.教师哲学视域下教师学习解析[J].教育理论与实践,2020,40(11):31-34.
[13] 陈莉,刘颖.从教师培训到教师学习:技术支持教师专业成长的途径与策略[J].中国电化教育,2016(4):113-119,127.
[14] 胡庆芳.中小学教研活动课程化的思考与实践[J].教育理论与实践,2014,34(29):6-8.
[15] GERALD J L, RONALD D M, KEVIN M N, et al. The improvement guidea-practical approach to enhancing organizational performance [M]. San Francisco, CA: Jossey-Bass, 2009: 23-25.
[16] 陈琦,刘儒德.教育心理学[M].北京:高等教育出版社,2005:156-157.
[17] 戴尔H 申克.学习理论:教育的视角[M].韦小满,译.南京:江苏教育出版社,2003:76-85.
[18] POPESCU C R, POPESCU V A. The Assessment methodology PDCA/PDSA-A methodology for coordinating the efforts to improve the organizational processes to achieve excellence [J]. Challenges of the Knowledge Society, 2015, 5 (1): 693-696.
[19] STIGLER JW, HIEBERT J. Lesson study, improvement, and the importing of cultural routines [J]. ZDM, 2016, 48 (4): 1-7.
[20] LEWIS C. What is improvement science? Do we need it in education? [J]. Educational Researcher, 2015, 44 (1): 54-61.
[21] 韩笑,陈唤春,李军.教育改进学的创建与中国探索:方法论[J].清华大学教育研究,2020,41(3):34-41,65.
[22] National Association for the Study of Educational Methods. Lesson study in Japan [M]. Tokyo: Keisuisha co., Ltd., 2011: 1-15.
[23] 杨玉东.日、港、沪三种教学研究活动及启示[J].教育发展研究,2006(11):43-47.
[24] 齐健,李秀伟.教师课例研修的理论视野与实践要义[J].中国教育学刊,2012(12):77-80.
[25] 陈欣,李高峰,许桂芬.课例研修模式的特点、操作要素及建议[J].课程·教材·教法,2015,35(10):115-119.
[26] 徐晓东,何小亚,周小蓬,等.专家进课堂项目促进教师专业发展的研究[J].中国电化教育,2016(1):95-102.
[27] 廖晶,王光明.中小学数学教师“五高”培训模式的建构与应用[J].数学教育学报,2017,26(5):17-19.
[28] 沈威,陆珺.数学教学课例研究的若干形态[J].数学教育学报,2018,27(3):76-80.
[29] 陈沫.乡村数学教师“TOP+X”培训模式的建构与应用——以贵阳学院乡村数学教师“国培计划”实施为例[J].数学教育学报,2018,27(2):87-92.
[30] 陈向明.跨界课例研究中的教师学习[J].教育学报,2020,16(2):47-58.
[31] 徐晓东,李王伟,赵莉.专家引领下现象为本的课例研修模式及其效果研究[J].电化教育研究,2020,41(10):106-113.
[32] 韩冰.新高考等级赋分制在教学管理中的应用研究[J].天津师范大学学报(基础教育版),2021,22(2):27-30.
[33] 成丽宁,李晓华.民族地区中小学教师专业素养结构模型研究[J].民族教育研究,2021,32(1):129-135.
[34] 李让美,郭衎,曹一鸣.学生合作问题解决过程中的教师注意——基于15位职前数学教师的眼动研究[J].数学教育学报,2021,30(2):42-47.
[35] 赵思林,潘超.中学数学教师核心素养及构成要素[J].数学教育学报,2021,30(2):48-54.
[36] 陆珺,胡晴颖.论数学解题教学的教学[J].数学教育学报,2021,30(2):55-60.
[37] 刘喆,练飞芸.数学师范生信息化教学能力发展研究——基于实证分析的视角[M].数学教育学报,2021,30(1):91-96.
[38] 郑毓信.新一代数学教育研究者的成长[J].数学教育学报,2020,29(6):1-6.
[39] 尹瑶芳.小学数学教师图形与几何知识状况调查——以上海市浦东新区为例[J].数学教育学报,2020,29(5):46-51.
[40] 李卓,鲍建生.论设计研究:“内涵”“类型”“过程”与“应用”[J].数学教育学报,2020,29(5):52-57.
[41] 刘桂宏,饶从满.职业生涯视角下初中数学教师PCK发展趋势及特征[J].数学教育学报,2020,29(5):58-63.
[42] 李昌官.元指导:基于素养与单元的学习指导范式[J].数学教育学报,2020,29(5):64-68.
[43] 叶志强,张旭.基于E-Prime的职前小学教师口算素养测评研究[J].数学教育学报,2020,29(5):69-74.
[44] 罗成禹.夯实学科基础 突出能力考查 打造高素质教师队伍——中小学教师资格考试数学学科知识与教学能力“学科知识”模块考情分析与测评[J].数学教育学报,2020,29(3):51-56.
[45] 吴琼,高夯.教师专业知识对高中数学教师教学实践影响的调查研究[J].数学教育学报,2020,29(3):57-62.
[46] 连四清,伍春兰.认知负荷理论与数学教学样例设计[J].数学通报,2005,44(11):24-26.
[47] GROSSMAN P L. The making of a teacher: Teacher knowledge and teacher education [M]. New York: Teachers College Press, 1990: 7-9.
[48] 汤丰林.不堪重负的教师培训:反思与出路[J].当代教师教育,2016,9(1):78-83.
[49] 裴淼,李肖艳.成人学习理论视角下的“教师学习”解读:回归教师的成人身份[J].教师教育研究,2014,26(6):16-21.
Research on Advanced Study of Middle School Mathematics Lessons Based on Teacher Learning under the PDSA Perspective
WU Chun-lan
(Mathematical Department, Beijing Institute of Education, Beijing 100120, China)
In view of the insufficiency of trainees’ participation in “lesson case study” during current training of mathematics teachers, this study constructed two rounds of the framework for the PDSA lesson case study framework and studied the process in several long-term training projects of middle school mathematics teachers. Using an example on the topic of factorization, the main research process and effect are explained. Supported by two rounds of the PDSA lesson case study framework, this study refined the “Six-Three” dialogue framework of teaching design; contributed to the study and research of mathematic teachers based on lesson cases using the background of big unit; taking the roles of students, teachers, and author, activated mathematics teaching content from four dimensions of knowledge and skills, mathematical thinking, problem solving, and emotional attitude; and realized a deep transformation from teaching content of mathematics academic form to educational form.
teacher learning; lesson study; advanced lesson study; factorization
G420
A
1004-9894(2021)03-0078-05
伍春兰.PDSA视域下基于教师学习的中学数学课例研修研究[J].数学教育学报,2021,30(3):78-82.
2021–05–11
中国教育学会一般规划课题——PDSA视域下的课例研修对数学教师专业发展影响研究(201900312201B)
伍春兰(1963—),女,广东台山人,副教授,主要从事数学教育研究.
[责任编校:周学智、陈隽]
——评《批判教育学的当代困境与可能》

