分数概念表述和分数除法运算的比较研究及其对教学的启示
赵 莉,王春英,史宁中
分数概念表述和分数除法运算的比较研究及其对教学的启示
赵 莉1,王春英2,史宁中1
(1.东北师范大学 数学与统计学院,吉林 长春 130024;2.东北师范大学附属小学,吉林 长春 130024)
分数教学的难点在于概念表述和除法运算,重点在于关注分数与整数教学的一致性.选取部分国家和中国主要版本的小学数学教材,对“分数的概念与大小”和“分数除法”两方面内容进行比较研究,探究分数意义的表述以及分数除法算理与算法的逻辑联系.在比较研究的基础上提出“分数概念”与“分数除法”教学的新设想,并进行了教学设计和实施,发现实验班的学生能够接受逻辑支撑的算法与算理.作为研究的结论,重新构建了分数除法的教学框架,希望能够为中国小学数学教学改革提供有益借鉴.
小学数学;分数概念;分数除法;比较研究;逻辑推理
在小学数学教学中,分数意义的理解与分数除法的把握一直都是教学的重点与难点,也是数学教育研究的热点,近些年的研究主要围绕分数定义表达[1]、分数意义理解[2]、分数除法编排[3]等问题展开.
事实上,分数教学的研究更应当关注与整数、小数教学的整体性和一致性[4].为了把这个问题讨论得更清楚,这里对新加坡、日本、美国加州和中国主要版本的“分数的概念与大小”和“分数除法”两方面内容进行比较研究,在研究结论的基础上重新构建了基于整数、分数和小数一体化思想的分数教学,特别是分数除法的教学框架,并进行了教学设计和实施,得到了探索性结论,希望能够为中国小学数学教学改革提供有益借鉴.
1 研究问题与研究对象
研究问题是“分数的概念与大小”和“分数的除法”两个方面教学内容的表述,研究对象选取了4个国家适用范围广、学制6年的主要版本教材,版本如下.
国内教材,人民教育出版社出版的《小学数学(三~六年级)》;国外教材,日本东京书籍株式会社出版的《新算数(二~六年级)》、新加坡Marshall Cavendish Education出版的-、美国The McGraw-Hill Companies出版的.
4套教材的比较,关注3个具体问题:分数的概念与大小的表述;分数的意义与分数除法的关联;分数除法算法与算理的逻辑联系;分数的意义与分数除法的关联.
2 分数的概念与大小比较
分数概念源于分数的意义,大体有5种构想[5],部分/整体、比率、商、度量和运算,或者5种形式表达[6]:部分/整体、子集/集合、数轴上两个整数间的一点、除法运算的结果、两个量的比.弗赖登塔尔认为:“通过等分和测量引入分数,目的在于体现分数的直观形象……事实上,测量产生的是小数而不是分数.”[7]也可以认为:“分数的本质是一个无量纲的数.虽然可以把分数看成除法运算的一种表示,但分数本身是数而不是运算.分数的本质在于真分数,这样的分数有两个现实背景,一个是表达整体与等分的关系.一个是表达两个数量之间整数的比例关系.”[8]因此,可以把分数理解为两个数量之间倍数关系的表达.
综上所述,分数概念的表达具有多重性,只有确切把握分数的本质特征、各种表达的相互关联,才能保证分数概念述说的逐渐深入,体现概念形成过程的抽象性.
分数的认识需要同时关注分数大小的比较.这是因为“与研究对象的存在性相比,研究对象之间的关系更为本质”“在现实生活中,数量关系的核心是多与少,人们把这种关系抽象到数学内部,这就是数的大与小”[9].事实上,也只有通过大小关系的比较才能真正理解分数的意义.下面分析4套教材“分数意义”的表述.
2.1 分数意义表述的相同之处
(1)都体现分数意义的多样性,都进行分数大小的比较.
关于分数的意义,都是通过等分一个整体的物体认识几分之一和几分之几,拓展到等分一个集合的物体认识子集所占比例,都是用数线上的点表示分数,用分数表示整数除法的商,但侧重点有所不同.认识分数的同时都比较分数的大小,大体采用等分图形、数线上的数比较同分母分数,然后通分比较异分母分数.
(2)直接给出分数与除法的关系,都没有论证其中的道理.
2.2 分数意义表述的不同之处
(1)强调的重点不同.
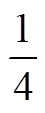
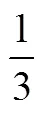
加州教材强调等分.用文字语言定义分数,说明分子分母各自的含义,借助图形说明;由一个物体拓展到一个集合,仍然强调部分与整体之间的关系.对于分数的其它意义比较弱化.
(2)与除法关系表述不同.
人教版教材通过实例解释除法与分数的关系,把整数除法问题分为两种情况,一种情况是平均分,如“把3个月饼平均分给4人,每人分得多少个?”另一种情况是数量比,如“小新家养鹅7只,养鸭10只.鹅的只数是鸭的几分之几?”说明两种情况分别表示整体与等分关系和数量的比例关系,结合画图解释可以用分数表示除法的商.
日本教材借助图形解释平均分,用语言解释除法算式的商可以用分数表示,并将数量关系统一为倍数关系,强调分数倍与整数倍的意义一样,因此用分数表述原来大小的倍数时,要用除法.

加州教材用分数表示整数除法的商,突出分数可以转化为小数,即任何一个分数都可以通过分子除以分母的方式转化为小数,并且用竖式计算的方法把假分数转化为带分数.
3 分数除法的算法与算理
分数除法算理的解释一直备受关注, 关键是如何使得算理与算法实现数学化的一致性.数学化是弗赖登塔尔提出来的,张奠宙更是强调数学学习的过程就是数学化的过程[10].下面,基于数学化的一致性分析4套教材中分数除法的表述.
4套教材分数除法的表述路径相似,都是结合具体问题,通过画图解释算式的步骤,然后归纳分数除法的算法,即除以一个分数等于乘以这个分数的倒数.但编写理念与表述形式各不相同.
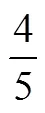
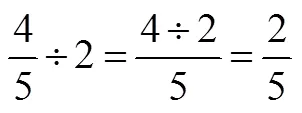
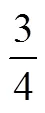
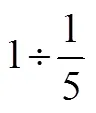
上面的表述,都是就个案解释除法的意义,均没有呈现现实问题数学化的过程,即没有讨论分数除法与整数除法之间的关联,也没有讨论除法是乘法的逆运算.
4 结论与启示
4.1 分数的认识要突出分数单位
参考4套教材的表述,关于分数的认识,分多层次多年级进行教学是合理的.无论是哪个层次的教学,都要突出分数单位,这可以为认识假分数做铺垫,与整数和小数的认识保持一致.通过后面讨论可以看到,设计3个层次比较合理.
4.2 要关注分数与整数除法的关系
虽然4套教材都用相当多的篇幅解释分数除法算法的理由,但都没有引导学生认知分数与整数除法之间的关系.事实上,虽然可以把整数除法、分数以及比表示成相同的形式,但3者之间存在本质差异,是需要进行转换的[11].通过后面讨论可以看到,一个合理的方法,应当在学习分数除法运算之前,专门设置“整数除法可以表示成分数形式”这样的教学内容,进而体现分数除法表述的数学化.这是因为,虽然“除以一个分数等于乘以这个分数的倒数”这个算法对分数成立,但首先是对整数成立,即“除以一个数等于乘以这个数的倒数”.
4.3 确立倒数概念是必要的
人教版教材和加州教材都明确了倒数概念,并且安排一定的课时引导学生理解倒数,这是非常必要的.这不仅是因为分数除法的算法表达中涉及倒数,更重要的,是因为倒数概念使得用乘法运算定义除法运算成为可能,进而使得整数除法可以表示为分数形式,如后面的讨论,倒数可以构建整数除法与分数除法之间的桥梁.
5 重新构建分数的教学框架
基于对4套教材的分析,采纳合理的表述,修订不合理的表述,重新构建分数的教学框架;虽然主要是针对分数认识和分数除法的内容进行阐述,但也涉及到分数教学的其它内容.
5.1 分数的教学分3个层次
本质是理解分数,3个层次依次为:通过情境认识分数;通过加减法认识分数;通过乘除法认识分数.无论是哪个层次,都要突出分数单位,使得无论是分数的认识还是分数的运算,都与整数、小数保持一致,进而让学生感悟数学的整体性,数学不是各说各的理.具体内容安排如下.
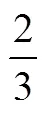
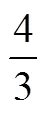
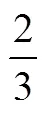
5.2 讲授分数除法要回顾整数除法
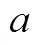
因此,分数除法教学的关键是说明上式第一个等式成立.为了简单明了,用数字表述推理过程如下.
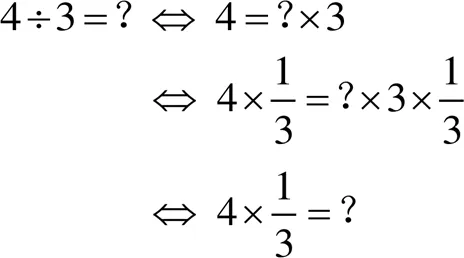
第一个等价关系成立是根据“除法是乘法的逆运算”,第二个等价关系成立是根据“等式的基本性质”,第三个等价关系成立是因为已经学习了分数的乘法;最后,根据“等量的等量相等”这个基本事实得到结论.这种完全基于符号和基本事实的说明就是数学化的过程.因为在上面的说明中可以把除数换为分数,这样,分数除法运算就是整数除法运算的延伸,这就是反复强调的运算的一致性.然后回归现实,用合适的案例进行说明.
可以看到,要实施这样的教学,需要倒数的概念,如前面所强调的那样;此外,还需要低年级的教学有所铺垫,比如,需要逐渐但明确地让学生知道“减法是加法的逆运算”“除法是乘法的逆运算”,事实上,广大的一线教师也是这样教的,比如“算减法想加法”“算除法想乘法”,现在需要用等式明确表达.
问题的关键是,小学生是否能够接受这样的说理,或者更确切地说,需要知道这样构想的分数除法的教学效果,研究者进行了相关内容的教学设计,并且进行了教学实验.
6 分数除法教学的教学实验
教学实验的目的是考察上一节设想的教学是否能被五年级学生接受,效果如何.教学实验的对象是东北师范大学附属小学五年级同一位数学教师的两个班级.把其中一个班级设定为实验班,一个班级设定为对照班,学生人数分别为42人和41人.教学实验由研究者本人担当,这样可以忽略教师的差异.实验内容是“分数与除法”教学,对照班按传统的教学方式,利用画图的方式解释除法算式可以用分数表示的道理,观察学生的接受程度和表现;实验班在学生画图理解的基础上,运用逻辑说理的方式解释除法运算的商可以用分数的形式表示,观察学生的接受程度和表现.具体教学设计和效果如下.
6.1 教学实验设计
在进行教学实验前,学生已经学习了分数的意义(一),都是原数学教师授课.在教学中,把分数的意义从一个物体的整体扩充到多个物体的集合,通过集合中的元素所占比例认识分数,体会单位“1”的不同,以及分数表示量的不同.
教学实验分为两个课时,第一课时讲分数的意义(二),第二课时讲分数与除法,都是教材要求的内容.两个班级的这两个课时都是研究者授课.
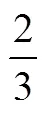
第二课时讲授分数与除法,首先让学生经历分物过程,运用不同方法把除法运算结果用分数表示,得到分数与除法的关系.
设计3个平均分的问题,背景是分披萨.问题情境分别为“把1个披萨平均分给2个小朋友”“把2个披萨平均分给3个小朋友”“把5个披萨平均分给3个小朋友”,提出的问题都是“每个小朋友可以分得多少个披萨”.
可以看到,第1问得到的结果是分数单位,这个结果可以为后面两个问题做铺垫;第2问得到的结果不是有限小数,启发学生思考整数除法与分数之间的关系;第3问作为教学效果的测试题目.
6.2 教学实验过程
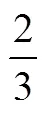

图1 学生完成第1问的情况
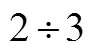

后半段教学进入实验阶段,两个班级采用不同的教学方法,教学目的都是让学生理解“整数除法可以表示成为分数的形式”.
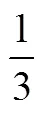
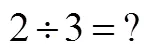
6.3 教学效果分析
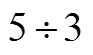
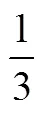
学生不确信所有的除法运算都可以转化为乘法的计算,因此对假分数形式的分数表达缺乏信心.
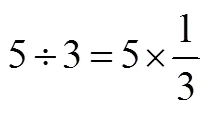
实验班学生经历了数学化的过程,通过逆运算理解除法与乘法的关系,得到除以一个数等于乘以这个数的倒数的算法,然后通过具体的例子解释数学结论的现实意义,有利于学生把握算理与算法的逻辑联系.对照班的大部分学生仍然停留在具象思维的阶段,没有上升到数学的一般.教学实验的结果表明,对于“整数除法可以表示为分数形式”的教学,适当引入逻辑说理的方法学生是可以接受的.
6.4 课后访谈情况
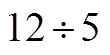

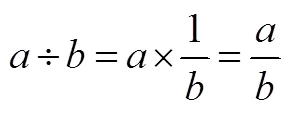
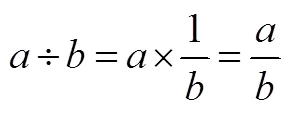
[1] 蒲淑萍.“中国美国新加坡”小学数学教材中的“分数定义”[J].数学教育学报,2013,22(4):21.
[2] 张丹,孙京红.整体建构分数意义的教学行动研究[J].数学教育学报,2015,24(2):22-26.
[3] 张平,彭亮,徐文彬.大陆与台湾小学数学教材中分数除法的编排比较[J].数学教育学报,2018,27(6):38-43.
[4] 史宁中.关于除数是分数或者小数除法的一个注[J].数学教育学报,2019,28(5):1.
[5] 刘儒德,杨伊生.儿童分数概念发展研究综述[J].内蒙古师范大学学报(教育科学版),2008(6):130-134.
[6] 张睆,辛自强.分数概念的个体建构——起点与机制及影响因素[J].数学教育学报,2013,22(1):29-32.
[7] 弗赖登塔尔.作为教育任务的数学[M].陈昌平,译.上海:上海教育出版社,1995:185.
[8] 史宁中.基本概念与运算法则:小学数学教学中的核心问题[M].北京:高等教育出版社,2013:5.
[9] 史宁中.数学基本思想18讲[M].北京:北京师范大学出版社,2016:3.
[10] 张奠宙.数学教育纵横[M].南宁:广西教育出版社,2018:100-101.
[11] 史宁中,娜仁格日乐.小学数学教科书中的比及其教学[J].数学教育学报,2017,26(2):1-5.
A Comparative Study of Fractional Conceptual Representation and Fractional Division and Insights for Teaching
ZHAO LI1, WANG Chun-ying2, SHI Ning-zhong1
(1. School of Mathematics and Statistics, Northeast Normal University, Jilin Changchun 130024, China;2. Primary School Attached to Normal University, Jilin Changchun 130024, China)
The difficulty of fraction teaching lies in conceptual representation and division operation, with a focus on the consistency of fraction teaching and integer teaching. This paper presents a comparative study of fractional concept and size and fractional division of major editions of elementary school mathematics textbooks from some selected countries and China as well as a further investigation of the representation of the meaning of fractions and the logical connection between fractional division arithmetic and algorithms. Based on the comparative study, we propose a new idea of “fractional concept” and “fractional division” teaching and conduct its instructional design and implementation. It was found that the students in the experimental class were able to accept the algorithms and arithmetic supported by logic. As a conclusion of this study, the teaching framework of fractional division was reconstructed in the hope that it can provide useful reference for the reform of elementary school mathematics teaching in China.
elementary mathematics; fractional concept; fractional division; comparative study; logical reasoning
G622
A
1004-9894(2021)03-0046-06
赵莉,王春英,史宁中.分数概念表述和分数除法运算的比较研究及其对教学的启示[J].数学教育学报,2021,30(3):46-51.
2021-05-10
国家社会科学基金教育学重大课题——新时代中国教育高质量发展的路径和对策研究(VFA190004)
赵莉(1990—),女,吉林松原人,博士生,主要从事数学课程与教学论研究.
[责任编校:周学智、陈隽]

