数学教师合作学习的效能研究——一个语义会话的分析

陈肖颖，章勤琼，Shin Bomi

数学教师合作学习的效能研究——一个语义会话的分析

陈肖颖1，章勤琼2，Shin Bomi1

（1．韩国全南大学 数学教育系，韩国 光州 61186；2．温州大学 教师教育学院，浙江 温州 325035）

合作学习对教师专业发展有积极作用，话语是教师合作学习过程中必不可少的要素之一．以“三角形重心”的教学知识为例，结合内容分析与时间序列分析两种方法，对教师通过合作学习所分享或更新的知识以及在这一过程中的话语线索进行分析．分析材料包括两个部分：一是教师在进行合作学习前后写的课堂录像观察反馈报告，二是在合作学习中讨论的话语．结果表明，合作学习能帮助教师对三角形重心的教学知识产生新的理解，研究还揭示了教师在合作学习过程中的话语线索：寻求信息或意见，建立观点，提供理由或证据，以及挑战观点或重新关注话题．

合作学习；教师专业发展；话语分析；时间序列分析

合作学习吸引了来自各个国家教师的高度关注，它能将教育创新纳入日常的教学实践，对教师的专业发展有重要作用．国际经合组织在2015年的报告中推荐将“鼓励教师通过专业发展或课堂实践进行合作”作为政策[1]．新加坡和美国的诸多研究结果表明，合作学习可以帮助教师提高对教学和学科内容知识的理解[2-4]，部分研究认为教师关于课堂行为的讨论与他们的专业理解有关[5]．这些研究为教师专业发展探索出一条可行的途径．然而，以往的研究大多采用了相当结构化的研究模型进行分析[6]，没有对过程中的细节进行深入挖掘．因此，教师在合作学习中的具体互动过程仍值得进一步研究．

教师学习的结果通常与概念化的干预特征相联系，如知识、技能或态度，而很少与教师的学习过程联系．以过程的视角进行研究可检验教师专业发展的有效性[7]，但单一地调查研究教师的讨论过程也不足以评价教师对专业知识的理解是否提升[8]．尽管Bakkenes等人[9]通过内容分析得出教师在合作学习中主动和自我调节的结果，并将教师的学习活动分类，但并没有揭示教师学习过程中具体有贡献的行为．而合作学习的时间性被明确认为是分析合作活动的一个重要视角[10-13]，如果忽视时间因素，仅靠内容分析不足以揭示教师知识提升的有效线索．结合内容分析与时间序列分析，对教师合作学习的过程进行研究，探讨合作学习是如何对教师、对专业知识理解产生效果的．

1 问题提出

1.1 文献综述

1.1.1 合作学习话语中的知识构建

知识构建是以合作学习为核心，致力于共享知识对象的建构与提升[14]．专业团体在认知活动中常常能提供友好的环境或社会结构，从而促进和维持专业发展[15]．现有研究表明，合作学习能对教师的工作或学习产生多方面的影响，如教师在工作或学习中的信念与个性、数学教学知识以及教学实践都会在合作情境下发生变化[16]．其中，教师的专业知识在合作学习情境下的变化尤为突出．Heller等人[17]对基于合作的专业发展项目的影响进行了比较研究，并发现了教师概念知识的增加．Huang和Shimizu[16]的研究认为课例研究是引起教师专业知识变化的背景因素．教师可以通过有效的合作学习方式，相互分享和构建知识，并利用持续的、动态的和互动的话语来进行支持[18]．

合作的特征体现了互动的力量，小组成员在互动中进行了思想交流，为教师专业发展带来了优势．Vygotsky[19]指出人的内部心理（intramental）功能是通过与他人的社会互动和交流形成的．这是合作学习的一个共同特征，特别是对于类似教师群体这样具有共同目标的专业团体．从这一概念出发，合作学习被视为教师专业知识的交流和构建的一个途径，分析其交流的内容或质量则可以提供一个可行的方法来揭示某些生产性学习成果或效果的细节[8]．在合作交流中，话语常扮演重要的角色．大量的研究将话语作为一种工具，去理解他人的知识，并促进人产生创造性的想法[20]．从最初的提议开始，人们可以通过澄清或比较不同的想法来引发讨论；当小组成员有疑问时，为了积极推动该提议，成员们的讨论和话语便是重要的特征和支持条件[21]．然而，在合作学习情境中，教师知识构建的细节和特征需要更为清晰的证据．以往研究大多采用定量的方法，如调查法[22-23]或在教师合作专业发展项目中进行实验[24]．而跟踪合作学习的过程有多种途径，其中包括了话语等大量丰富的信息，但很少有研究能从繁多的数据中解析出与教师知识构建相关联的明确标志或线索．

1.1.2 内容分析与时间序列分析

如何理解和分析面对面或在线环境下的学习过程中所出现的话语和动作是合作学习研究中的关键问题[25]．在线系统中收集操作日志并不困难，线下的录像、录音也有迹可循．其中文本或语言等材料常出现在研究中，包括各种类型的解释和主题[14]．内容分析对日志、语言的应用是相对流行和行之有效的[27]，它可以在确定的时间点上评估群体知识．通常使用统计方法进行定量分析，也可从定性角度挖掘文本内容．相对简单和客观的形式是考虑主题或词语的频率，且具有明确的特征性．然而，定量的测量和分析很少能考虑群体间产生的共享知识，也无法得出有助于知识构建的动态和互动过程[26]．Mercer[28]倡导合作学习等共同的智力活动，提倡定性和定量方法的互补，提出了社会文化话语分析（SCDA）来研究课堂话语．利用SCDA的理念，Vrikki和Warwick[29]还编制了具有较高可靠性的用于识别教师学习话语的编码表．然而，话语的有效性仍很难厘清，仅靠内容分析而不考虑时间性，很难得出有帮助的结论．

有关合作学习的时间性近年来得到诸多研究关注，如关于在线讨论中知识构建的时间模式[30]．应用最为广泛的方法是时间序列分析，它有助于准确把握学习者的潜在行为模式，从行为视角阐释学习效果产生的原因[36]．例如Chen等人[26]运用该方法探究出识别产生知识构建的话语线索的序列模式，并倡导应该更多地利用学习的时间性来进行分析．这种对学习过程中与学习者行为或互动相关的数据、学习者的个人信息以及学习环境的分析与解释[31]的方法能更加深入理解和分析合作学习，揭示不同形式的学习行为模式，挖掘合作学习中知识构建的过程．例如，确定与内容、同伴和导师的互动之间转变的显著性，并得到学生的学习行为模式和时间变化[32]；通过收集和分析教师与学生的讨论活动来确定学生行为的转变，从而展示出在课堂上实施的特定教学策略的干预效果[33]；在以证据为中心的设计框架中，序列分析可用来分析学生的行为模式，为评估学生的特定能力提供微观层面的探索方向[34]；也能确定不同学习形式下的学生行为模式，如在线互动平台、面对面同步同伴辅导系统等[35]．但这些研究多集中在学生的合作学习或师生的互动行为上，对教师群体的合作学习的研究明显不足．因此，可利用时间序列分析等可深度挖掘学习过程的方法，来获得如话语线索等特征作为观察合作学习过程中知识构建的指标，并测定和分析教师群体在合作学习过程中的效果．主要应用时间序列分析探索教师在合作学习的互动讨论情境中专业知识的变化情况．

1.2 研究问题

合作学习在教师专业发展中的应用与研究愈加流行，但仍然缺乏形成这种发展的过程中的证据．群体中的教师学习对教师知识的发展有积极影响，但在某种程度上这种效果也不一定会产生[29]．由于中学数学内容中的三角形的重心常被用做课堂探究活动进行教学，而其定义和性质常被中学数学教师误解[37]．因此，选取中学数学三角形重心的教学为例，对教师在合作学习下讨论的特定数学内容的过程进行探讨．具体来说，需要解决以下问题．

（1）教师在合作学习前后对三角形重心的课堂教学的相关知识理解有何变化？

（2）在合作学习过程中，教师讨论三角形重心的教学知识时的话语有什么特点？

2 研究方法

课堂录像学习有助于教师对教学过程的理解，并对教师专业发展有积极影响[38]．通过对教师观看课堂教学视频后与合作学习后的反馈报告进行内容分析，以检测教师对三角形重心的相关教学知识的理解是否有变化；然后进行合作学习并利用时间序列分析对教师在讨论过程中的话语进行深入挖掘，探寻引起教师对三角形重心的相关教学知识变化的话语线索．

2.1 研究设计

2.1.1 被试

参与研究的被试是4名韩国中学在职数学教师（男性1名，女性3名），平均年龄30岁，均在韩国国立大学师范学院数学教育系参加过数学教育硕士专业课程，有近十年的中学数学教学经验．

2.1.2 研究框架与过程

实验分为两部分进行．在第一部分中，4名教师先观看关于“三角形重心”的课堂教学视频，对这堂课的相关教学知识的理解各自写反馈报告（pre-report）；在第二部分中，4名教师就所观看的视频中教师的教学进行40分钟左右的讨论，讨论结束后再写一次反馈报告（post-report）．教师们所观看的视频是以三角形重心为主题的探究活动课的课堂录像，主要探究了三角形重心的定义和性质（视频来自2012年韩国京畿道教育研究院优秀课视频，详细介绍见附录）．教师们所写的反馈报告是基于自己对三角形重心及其教学的认识与理解对视频中教师的教学的判断或意见．教师们的讨论过程以音频和视频两种形式全程录制保存，并进行脚本记录．实验的具体实施步骤可分为：（1）观看课堂教学视频；（2）撰写反馈报告；（3）进行小组讨论；（4）再次撰写反馈报告．研究框架呈现如图1所示．

图1 研究框架

2.2 研究工具

2.2.1 用于分析教师反馈报告的框架

采用Margaret等人[39]提出的中学教师几何评估工具（GAST）来分析教师对几何教学的理解．GAST给出了中学几何教学知识评估框架（表1），它将几何教学知识分为3类：中学几何知识，高等几何知识（即超出中学几何范围的相关知识，具体内容见表1），以及几何教学知识．由两位具有一定数学教育研究经验的专家对4名教师的反馈报告中的内容进行分析、分类，并统计各分类观点出现的频次．如果报告中出现有关中学几何或中学课程标准中所要求教授的几何内容，则这些反馈意见则被分类到中学几何知识；如果涉及了中学之后的几何知识，则被分类到高等几何知识；而有关几何教学的内容则被分类到几何教学知识．

表1 中学几何教学知识评估框架

2.2.2 用于分析教师话语的编码表

Vrikki和Warwick[8]的研究提供了一个可靠度较高的编码表，它通过描述和解释来表现合作学习过程对教师个体学习的影响．改编此编码表分析4名教师在合作学习时的话语，包含了4个独立的编码（表2）：寻求信息或意见，建立观点，提供理由或证据，挑战观点或重新关注话题．在进行实验之前，先对3名编码人员进行编码工作的培训，由这3位编码人员根据编码表对讨论过程的脚本内容进行编码，其间的Kappa系数为0.95，再用专门用于进行交互行为分析的软件GSEQ（General Sequential Querier）处理编码所得的数据．应用GSEQ软件分析的主要过程是：（1）按格式输入所有行为编码；（2）进行系统编译；（3）检验行为编码的一致性系数（Kappa）；（4）进行行为序列分析，得到行为转换频率表和调整后残差表；（5）根据调整后的残差表选取具有显著意义（残差值-score≥1.96）的行为序列来绘制行为转换图[40]．根据教师实际讨论的情况，根据讨论中的主要问题（表3）将讨论过程分为5个片段进行分析．

表2 教师合作学习的话语编码

表3 教师合作学习时实际讨论的主要问题

3 研究结果

3.1 对教师的反馈报告分析结果

两位专家根据表1对4名教师前后两份反馈报告中的内容进行分析、分类，统计各类观点出现的频次并记录在表4中．根据教师各自前后的观点频次，比较其观点的更新情况（updated）．若post-report中没有提及相应类别的观点或观点与pre-report中相同，则视为观点未更新，updated记为0；若post-report中提及了同类别的观点，且与pre-report中的观点不同或pre-report中未提及，则视为观点更新，因此可得出两种更新类型．

表4 4名教师各自反馈报告的观点出现频次

第一种是在前后反馈报告中在同一分类下有不同程度的意见或评论，如教师A在S2-b的观点：

教师A（pre-report）：这没找到重心的真正含义．学生们只知道用一根手指放在3条中线的交叉处，三角形就会竖立起来．（S2-b）

教师A（post-report）：……中线将原三角形分成了两个面积相等的三角形，这样的三条中线的交点就是重心，这种逻辑是不正确的．（S2-b）

在教师A的两份反馈报告中都对重心的含义表达了意见，是对高等几何知识中识别无效论点的能力的表现，归类于S2-b．而pre-report更关注学生的行为，post-report更偏向对重心性质的理解，即对数学内容的理解，从数学的角度对知识的进一步理解以及对无效论点的识别．

第二类仅在post-report中指出观点，但在pre-report中没有提出．例如，教师B的pre-report中没有关于S2-b的任何观点，但在post-report中教师B提到她学到了关于重心的知识：

教师B（post-report）：我发现我对重心不是很了解，听了教师C的发言后，我才知道“用中线平分面积来定义重心”并不是很好的解释．（S2-b）

通过教师们的小组讨论，教师B对与重心相关的无效论据有一定的认知与收获．此外，教师A在post-report中表达出对重心理解的拓展：

教师A（post-report）：……如果在本课结束时设计一个寻找圆或正方形的重心的环节，可能比将其设置为家庭作业要好．（S3-d）

教师A的上述观点将重心的讨论范围扩大到了圆和正方形，并给出了教学设计的具体建议．由此可以推断，合作学习有助于教师A对重心的教学设计，从而影响和激励了教师A对几何教学知识的理解．

3.2 对教师合作学习中话语的分析结果

根据教师合作学习时记录的脚本，编码人员根据表2对教师们的话语进行编码，利用GSEQ分析编码得到调整后的残差表（表5），表中的列表示起始话语的对应编码，行表示起始话语结束后随即发出的话语的对应编码．根据序列分析理论（Hou，2012），如果残差值Z-score≥1.96则表明该话语路径具有显著意义，所以表5中的显著的路径有D1→D2（2.33）、D2→D3（2.51）、D4→D4（5.97）．根据这些具有意义的话语数据绘制出话语转换图（图2），图中的箭头表示从一个编码到另一个编码的转换．从话语转换图可确认话语路径的典型逻辑：寻求信息或意见→建立观点→提供理由或证据，即D1→D2→D3．而D4→D4说明挑战他人观点或重新聚焦谈话主题在教师们讨论期间有高频次的表现．

表5 调整后的残差

图2 话语转换

从话语线索（D1→D2→D3）可以看出，教师可根据自己的先前知识，对所观看的课堂录像提出自己合理的看法．从记录的脚本中也可以找到以下证据：

教师A：让我们来谈谈重心的性质吧！（D1）

教师C：这太糟糕了．如果提前试一下会更好，但这一次是……实际上可以简单地确认的，但它变成了这样．（D2、D3）

此外，D4→D4表明教师在讨论过程中提出挑战性的想法或重新聚焦谈话的近乎辩论的场景，脚本中也有所呈现：

教师D：如果不那么统一地让学生做小组活动，不是更好吗？实际上，给学生更多的时间会更好，但显然不可能．（D4）

教师A：我们以后再谈这个问题．我只是觉得深入研究“重心”会更好．（D4）

针对教师们讨论的主要问题分成5个片段，将每个片段单独进行序列分析，得到了各自的话语转换图（如图3所示）．片段1的话语转换路径与图2中的主话语路径一致，片段3和片段5中没有出现大于1.96的残差值Z-score，无法绘制话语转换图，而片段2的话语路径D3→D1（1.96）和片段4的D3→D4（2.49）．这非常值得注意，因为D3之后出现了两种话语转换．换言之，教师的话语是以寻求信息或意见、建立观点、提供理由或证据为主话语路径，并有重复进行挑战或重新聚焦主题以及再次寻求信息或意见作为支线话语路径．

图3 各片段话语转换

在片段2中，教师们阐述了对该课堂录像中重心教学的理解．教师C表明了她自己关于重心的观点，并对视频中教师的解释方法表示赞同，但教师D对视频中的方法提出质疑，要寻求更多的确认，随后教师C进一步澄清．教师们通过话语来共享与建构知识，其对话过程如下：

教师C：（视频中的教师）对三角形的解释可能是正确的．但是，将多边形的面积分成两半的线的交点并不是多边形的重心．重心是旋转力为零的点，就像杠杆原理中的支点一样．（D3）

教师D：在一个多边形里？这里不是指这个意思吧？（D1）

教师C：是的．当你要确定一般图形的重心时，把图形分成两半的想法有点误导……（D2）

这部分脚本内容教师B在post-report中所写的关于重心的解释内容完全一致，这是教师在合作学习中知识共享和构建中很明显的证据．除了D3→D1这一支线之外，挑战或重新关注话题也可以是加深讨论和解释的富有成效的路径，如片段4的脚本所示：

教师C：……我认为它们是相似三角形，但我会让学生写下具体的长度并指出来，但（视频里的）教师没有提到……（D3）

教师A：（打断教师C）她提到了．（D4）

教师B：视频中教师确实提到“可能会有一些错误，不一定只是2∶1的比例”．（D3）

教师C阐述了她对视频中教师教学的看法，并给出了具体原因，她认为教师没有给出相似三角形的细节条件．但教师A直接打断了教师C的讲话，并指出教师C提供的证据不准确，质疑教师C的推理．随后教师B提供了明确的信息，并直接陈述了视频中教师的话．通过展示教师对相似三角形性质识别的具体证据，也说明了教师B对教师C的解释有异议．教师们通过提出质疑或重新关注话题可以澄清推理证据中错误的思路，而直接表达质疑或挑战有助于营造讨论的氛围，从而分享信息、构建知识．跟随合作学习中话语的转换路径，可以确定教师们在合作学习中对教学重心有了不同的或新的理解．

4 讨论与启发

尽管合作学习已被许多国家所认可，但仅有的研究结果还不足以阐述教师合作学习的具体发生过程，大多数采用单一分析方法，仅强调合作学习的结果或效果．这里利用GAST框架对教师观看课堂视频后的反馈报告内容进行挖掘，对教师在前后反馈报告中对三角形重心的教学知识的变化情况进行内容分析；运用时间序列分析从时间性的角度呈现话语转换路径，在一定程度上揭示了教师获取信息和开展讨论的细节要素，从而探究到教师拓展专业知识，加深对三角形重心教学相关知识的理解的发生过程．

具体来说，研究中分析了教师们进行合作学习前后的反馈报告．从GAST的框架来看，在合作学习之后，教师对如何进行重心教学的理解确实得到了更新，特别是关于高等几何知识和几何教学内容的部分．教师A和教师B的变化尤为显著，教师A增加了对几何教学内容的认识和感悟，并尝试进行课后扩展的教学设计，这是非常明确的证据；教师B在合作学习中并没有太多表达，但在其反馈报告中展示出在合作学习过程中的投入与参与，并表达了合作学习对自己专业知识的提升和帮助，尤其让她发现了自己在高等几何知识方面的不足．从片段2的脚本可知，在合作学习之后，教师B的反馈报告中有一个观点与合作学习之前教师A提供的观点一致，这也足以说明教师的讨论促进了知识共享和创意的产生[20]．

教师们在合作学习中进行了对话和讨论，其话语包括了寻求信息或意见、建立观点、提供理由或证据、挑战观点或重新关注话题．Vrikki等人[8]在忽略时间因素的情况下提出了这些话语特征[26]．这里用时间序列分析法来强调讨论期间的话语转换．通过序列分析揭示了话语路径D1→D2 →D3，表明了寻求信息、建立观点和提供证据的典型话语逻辑，而D4→D4显示了挑战观点或重新关注话题的重要性．此外，在D3之后或有两种话语转换，也提供了在提供理由或证据之后的两条支线路径：（1）D3→D1，寻求更多的信息或意见；（2）D3→D4，继续挑战观点或再次回到话题．

以往的研究采用了大量的脚本材料和文件，它们涉及了相当庞大的信息量[14]，这里通过将教师的反馈报告和话语分析联系起来，分析教师的专业知识通过合作学习产生的变化，从而以微观视角揭示数据的意义．混合使用内容分析和时间序列分析两种方法是将质性分析和量化分析结合的实践探索．针对教师合作学习的过程，选择两种数据处理方式：一是对话脚本，这是质性研究中常用的数据类型，并对脚本内容加以分析；二是将对话内容进行时间序列分析得到教师的话语线索，用量化的方法对教师讨论中的话语进行分析．由此对同一过程进行不同资料来源和分析比较，将分析结果加以整合，可以更加深化对研究的认识或修正，也是对质性研究效度的保证和检验．两种方法互相补充，扬长避短，是混合研究方法在实践中的重要特征．研究中印证了混合研究方法中的并行三角互证策略[41]，以反馈报告和话语分析两种形式呈现教师在合作学习中产生的知识变化，既为混合研究提供了一个数据分析整合的实证案例，也为合作学习效能的深度挖掘提供了一条能与质性研究相互验证的量化证据．

合作学习可以给教师共享和构建知识创造良好条件．教师们的反馈报告中反映出，合作学习为教师提供了获得更深层次几何教学知识的机会，拓宽了相关设计课程的思考范围，有利于教师的专业发展，也激发了教师的创造力．合作学习中教师们的话语路径勾画出他们讨论的逻辑．除了主话语路径，挑战观点和寻求信息在路径中起着重要的作用，也体现了近乎辩论的情境能给教师们带来更多的启发，经历头脑风暴似的观点碰撞，加深对关键概念和知识的理解，从而有助于教师的专业发展．

[1] SCHLEICHER A. Schools for 21st-century learners strong leaders, confident teachers, innovative approaches [C] // Proceedings of the International Summit on the Teaching Profession. Paris: OECD Publishing, 2015: 56-60.

[2] 沈威，陆珺．数学教学课例研究的若干形态[J]．数学教育学报，2018，27（3）：76-80．

[3] 陈蓓．课例研究与教师数学学科教学知识（MPCK）的发展[J]．数学教育学报，2016，25（4）：74-78．

[4] LEWIS J M, FISCHMAN D, RIGGS I, et al. Teacher learning in lesson study [J]. The Mathematics Enthusiast, 2013, 10 (3): 583-620.

[5] WARWICK P, VRIKKI M, VERMUNT J D, et al. Connecting observations of student and teacher learning: An examination of dialogic processes in lesson study discussions in mathematics [J]. ZDM Mathematics Education, 2016, 48 (4): 555-569.

[6] HORN I S. Attending to problems of practice: Routines and resources for professional learning in teachers’ workplace interactions [J]. American Educational Research Journal, 2010, 47 (1): 181-217.

[7] DESIMONE L M. Improving impact studies of teachers’ professional development: Toward better conceptualizations and measures [J]. Educational Researcher, 2009, 38 (3): 181-199.

[8] VRIKKI M, WARWICK P, VERMUNT J D, et al. Teacher learning in the context of lesson study: A video-based analysis of teacher discussions [J]. Teaching and Teacher Education, 2017 (61): 211-224.

[9] BAKKENES I, VERMUNT J D, WUBBELS T, et al. Teacher learning in the context of educational innovation: Learning activities and learning outcomes of experienced teachers [J]. Learning and Instruction, 2010, 20 (6): 533-548.

[10] DYKE G, KUMAR R, AI H, et al. Challenging assumptions: Using sliding window visualizations to reveal time-based irregularities in CSCL processes [C] // van AALST J, THOMPSON K, JACOBSON M J, et al. The future of learning: Proceedings of the 10th international conference of the learning sciences. Sydney: ISLS, 2012: 363-370.

[11] KAPUR M. Temporality matters: Advancing a method for analyzing problem-solving processes in a computer-supported collaborative environment [J]. International Journal of Computer-Supported Collaborative Learning, 2011, 6 (1): 39-56.

[12] MERCER N. The seeds of time: Why classroom dialogue needs a temporal analysis [J]. Journal of the Learning Sciences, 2008, 17 (1): 33-59.

[13] WISE A F, CHIU M M. Analyzing temporal patterns of knowledge construction in a role-based online discussion [J]. International Journal of Computer-Supported Collaborative Learning, 2011, 6 (3): 445-470.

[14] SCARDAMALIA M, BEREITER C. Knowledge building and knowledge creation: Theory, pedagogy and technology [C] // SAWYER K. Cambridge handbook of the learning sciences. New York: Cambridge University Press, 2014: 397-417.

[15] WEBSTER-WRIGHT A. Reframing professional development through understanding authentic professional learning [J]. Review of Educational Research, 2009, 79 (2): 702-739.

[16] HUANG R, SHIMIZU Y. Improving teaching, developing teachers and teacher educators, and linking theory and practice through lesson study in mathematics: An international perspective [J]. ZDM Mathematics Education, 2016, 48 (4): 393-409.

[17] HELLER J I, DAEHLER K R, WONG N, et al. Differential effects of three professional development models on teacher knowledge and student achievement in elementary science [J]. Journal of Research in Science Teaching, 2012, 49 (3): 333-362.

[18] ERYILMAZ E, van DER POL J, RYAN T, et al. Enhancing student knowledge acquisition from online learning conversations [J]. International Journal of Computer Supported Collaborative Learning, 2013, 8 (1): 113-144.

[19] VYGOTSKY L S. Mind in society: The development of higher psychological processes [M]. Cambridge: Harvard University Press, 1978: 79-120.

[20] MERCER N. Words and minds: How we use language to think together [M]. London: Routledge, 2000: 131-165.

[21] NEMTH C, ROGERS J, BROWN K. Devil’s advocate versus authentic dissent: Stimulating quantity and quality [J]. European Journal of Educational Psychology, 2001, 31 (6): 707-720.

[22] DOPPENBERG J J, DEN BROK P J, BAKX A W E A. Collaborative teacher learning across foci of collaboration: Perceived activities and outcomes [J]. Teaching and Teacher Education, 2012 (28): 899-910.

[23] RONFELDT M, FARMER S O, MCQUEEN K, et al. Teacher collaboration in instructional teams and student achievement [J]. American Educational Research Journal, 2015, 52 (3): 475-514.

[24] SAUNDERS W M, GOLDENBERG C N, GALLIMORE R. Increasing achievement by focusing grade-level teams on improving classroom learning: A prospective, quasi-experimental student of Title I schools [J]. American Education Research Journal, 2009, 46 (4): 1 006-1 033.

[25] LOSSMAN H, SO H J. Toward pervasive knowledge building discourse: Analyzing online and offline discourses of primary science learning in Singapore [J]. Asia Pacific Education Review, 2010, 11 (2): 121-129.

[26] CHEN B, RESENDES M, CHAI C S, et al. Two tales of time: uncovering the significance of sequential patterns among contribution types in knowledge-building discourse [J]. Interactive Learning Environments, 2017, 25 (2): 162-175.

[27] de WEVER B, SCHELLENS T, VALCKE M, et al. Content analysis schemes to analyze transcripts of online asynchronous discussion groups: A review [J]. Computers & Education, 2006, 46 (1): 6-28.

[28] MERCER N. Sociocultural discourse analysis: Analysing classroom talk as a social mode of thinking [J]. Journal of Applied Linguistics and Professional Practice, 2005, 1 (2): 137-168.

[29] WARWICK P, VRIKKI M, VERMUNT J, et al. Connecting observations of student and teacher learning outcomes: An examination of lesson study discussions in mathematics [J]. ZDM Mathematics Education. 2016, 48 (4): 555-569.

[30] WISE A F, CHIU M M. Analyzing temporal patterns of knowledge construction in a role-based online discussion [J]. International Journal of Computer-Supported Collaborative Learning, 2011, 6 (3): 445-470.

[31] HWANG G-J, CHU H-C, YIN C. Objectives, methodologies and research issues of learning analytics [J]. Interactive Learning Environments, 2017, 25 (2): 143-146.

[32] CHENG H N H, LIU Z, SUN J, et al. Unfolding online learning behavioral patterns and their temporal changes of college students in SPOCs [J]. Interactive Learning Environments, 2017, 25 (2): 176-188.

[33] CHIANG T H-C. Analysis of learning behavior in a flipped programing classroom adopting problem-solving strategies [J]. Interactive Learning Environments, 2017, 25 (2): 189-202.

[34] HU Y, WU B, GU X. Learning analysis of K-12 students’ online problem solving: A three-stage assessment approach [J]. Interactive Learning Environments, 2017, 25 (2): 262-279.

[35] TSUEI M. Learning behaviours of low-achieving children’s mathematics learning in using of helping tools in a synchronous peer-tutoring system [J]. Interactive Learning Environments, 2017, 25 (2): 147-161.

[36] 杨现民，王怀波，李冀红．滞后序列分析法在学习行为分析中的应用[J]．中国电化教育，2016（2）：17-23，32．

[37] SHIN B. A study about the characteristics of teachers’ viewpoint in analysis of an instruction: Focused on a centroid teaching-learning case [J]. Journal of Educational Research in Mathematics, 2016, 46 (3): 421-442.

[38] ALSAWAIE O N, ALGHAZO I M. The effect of video-based approach on prospective teachers’ ability to analyze mathematics teaching [J]. Journal of Mathematics Teacher Education, 2010, 13 (3): 223-241.

[39] MARGARET M, ROBERT N R, SUSAN P, et al. Predicting student achievement using measures of teachers’ knowledge for teaching geometry [J]. Journal for Research in Mathematics Education, 2017, 48 (5): 520.

[40] HORN I, LITTLE J. Attending to problems of practice: Routines and resources for professional learning in teachers’ workplace interactions [J]. American Educational Research Journal, 2010, 47 (1): 181-217.

[41] CRESWELL J W, CLARK V L P. Designing and conducting mixed methods research [M]. CA: SAGE Publications, 2011: 51-99.

2012年韩国京畿道教育研究院优秀课视频链接：

http://good.edunet4u.net/classMovie/player/pop/frame.jsp?movieID=178170&startTime=0&endTime=0

实验观看的课堂录像的内容流程

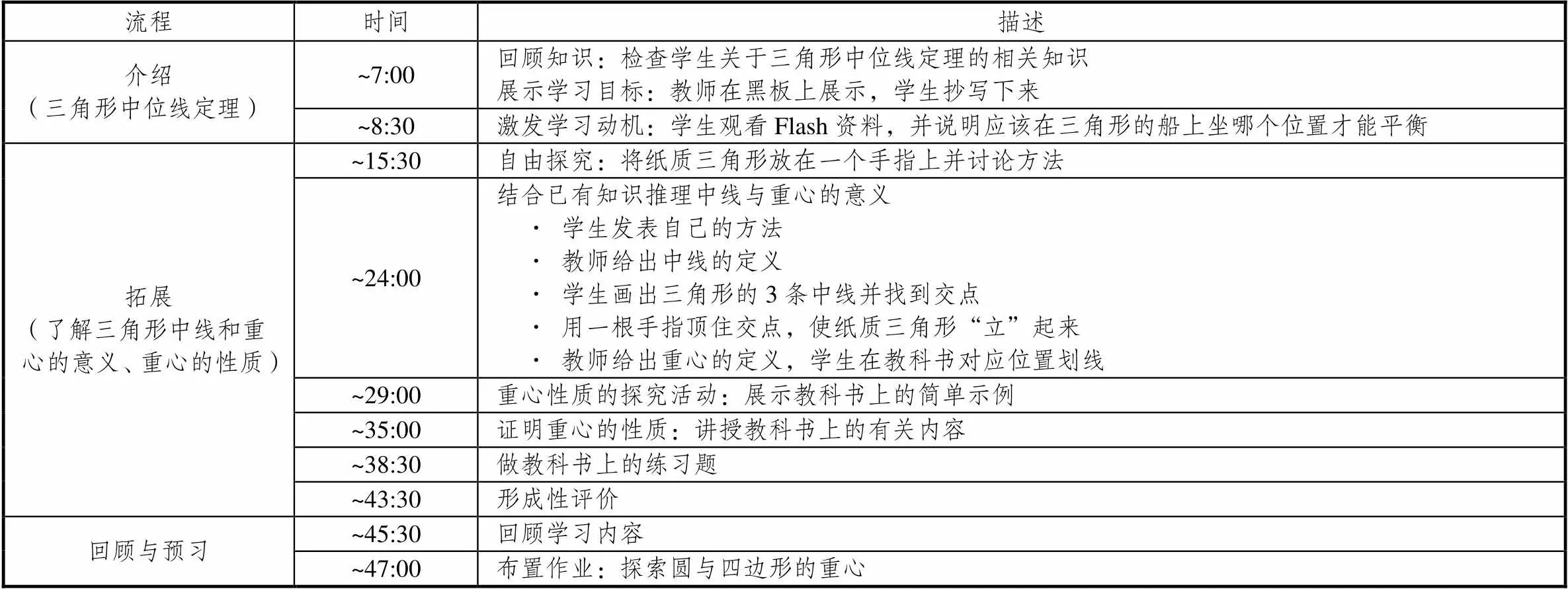
流程时间描述 介绍（三角形中位线定理）～7:00回顾知识：检查学生关于三角形中位线定理的相关知识展示学习目标：教师在黑板上展示，学生抄写下来 ～8:30激发学习动机：学生观看Flash资料，并说明应该在三角形的船上坐哪个位置才能平衡 拓展（了解三角形中线和重心的意义、重心的性质）～15:30自由探究：将纸质三角形放在一个手指上并讨论方法 ～24:00结合已有知识推理中线与重心的意义· 学生发表自己的方法· 教师给出中线的定义· 学生画出三角形的3条中线并找到交点· 用一根手指顶住交点，使纸质三角形“立”起来· 教师给出重心的定义，学生在教科书对应位置划线 ～29:00重心性质的探究活动：展示教科书上的简单示例 ～35:00证明重心的性质：讲授教科书上的有关内容 ～38:30做教科书上的练习题 ～43:30形成性评价 回顾与预习～45:30回顾学习内容 ～47:00布置作业：探索圆与四边形的重心

Study of the Effectiveness of Collaborative Learning of Mathematics Teachers: A Discourse Analysis

CHEN Xiao-ying1, ZHANG Qin-qiong2, Shin Bomi1

(1. Chonnam National University, Gwangju 61186, Korea;2. College of Teacher Education, Wenzhou University, Zhejiang Wenzhou 325035, China)

Collaborative learning has been highlighted as an effective method of teachers’ professional development in various studies. To disclose teachers’ discourse threads in the process of collaborative learning for developing their knowledge, this paper adopted two methods, including “content analysis” and “time-sequential analysis” of learning analytics. Such analyses were implemented for mining teachers’ updated knowledge and the discourse threads in their discussion during collaborative learning. The materials for analysis involved two aspects: one was from the video-taped lesson observation reports written by teachers before and after discussion, and the other was from their discourse during the discussion process. The results showed that teachers’ knowledge for teaching the centroid of a triangle was updated in the collaborative learning period and also that the discourse threads of teachers’ collaboration included “requesting information or opinions” “building on ideas” and “providing evidence or reasoning” with the emphasis on “challenging ideas or re-focusing talk”.

teacher collaborative learning; teachers’ knowledge; content analysis; time-sequential analysis

G40-03

A

1004-9894（2021）03-0018-07

陈肖颖，章勤琼，Shin Bomi．数学教师合作学习的效能研究——一个语义会话的分析[J]．数学教育学报，2021，30（3）：18-24．

2021-05-06

2020国家社科基金一般项目——大数据支持下的中小学合作型课堂组织形式建构研究（20BGL127）；浙江省高等教育“十三五”第二批教学改革研究——师范类专业认证背景下的《名师大讲堂》课程改革与实践研究（jg20190403）

陈肖颖（1991—），女，四川资阳人，韩国全南大学数学教育系博士生，主要从事数学教育、小学教育研究．章勤琼为本文通讯作者．

[责任编校：周学智、陈汉君]