基于数字栅格的河网小流域水质数学模型构建与应用

尹海龙，林夷媛，赵东华，石泽敏

（1.同济大学环境科学与工程学院，上海200092；2.中交上海航道勘察设计研究院有限公司，上海200120）

我国南方河网地区河流纵横，降雨丰富。随着污水收集率的不断提高，在城镇点源污染排放得到有效治理的情况下，村镇小流域地区的点源、面源污染排放成为水环境治理关注的问题。为此，需要建立耦合点源、面源排放与河道水质的数学模型，评估小流域内各类污染排放造成的水质动态响应，为污染物减排方案的制定提供科学依据［1-4］。

由于河网模拟范围较大，大多数情况下只能采用数值方法进行模拟［5］。河道水动力水质模型可以全面描述水体中的水动力—水质过程，但是难以准确获得面源污染的动态输入。因此，非常有必要将降雨产汇流模型和河道水动力水质模型耦合，以此建立河流和流域间的水力联系。Liu等［6］集成运用HSPF模型和EFDC模型模拟圣路易斯湾河口的水力水质情况，发现圣路易斯湾河口对密西西比河的水质具有重大影响；Li等［7］采用SWAT和EFDC耦合方法，研究了长潭水库1952—2010年间58年降水资料的频率响应与水质模拟分析；Thompson等［8］将水文模型MIKE SHE和水力学模型MIKE11进行耦合，每个时间段都进行数据的交换和迭代计算，通过这种模拟方式反映了坡面与河道洪泛区之间的相互作用关系；Narasimhan等［9］基于SWAT和WASP建立了水库水质评价综合管理模型，结果表明需要削减35%的TN和TP才能明显减少水库叶绿素a的浓度；朱瑶［10］等耦合运用SWAT与WASP模型，模拟苕溪流域面源污染负荷与水质响应情况。然而，物理性分布式水文模型还存在水文过程描述的过参数化问题，对空间信息的精度要求也很大程度上限制了模型的整体效果。

为了克服水文过程过参数带来的不确定问题并提高空间尺度上的模拟精度，本文采用栅格基础的数字高程模型（Raster-based Digital Elevation Model，DEM）构建方法，自动提取水系和划分子流域，以DEM栅格单元为基本模拟单元进行产流和产污计算，精细化描述降雨径流导致的面源污染排放与受纳水体间的空间响应关系，且应用方便。在自主研发的栅格化径流污染模型的基础上耦合开放式的河道水动力水质模型。开放式模型的优势在于有助于克服传统商业软件建模面临的智能通讯和系统集成性能差的问题，可进一步耦合智能算法，为实现参数自动率定、污染物精准溯源等奠定基础［11-12］。以常州市武进港小流域为例开展实证研究，对河网水质进行日尺度的动态模拟和精准预测。

1 模型的基本原理

1.1 水动力水质模型

1.1.1 一维非恒定流模型

对于河网地区而言，河道纵向长度远大于其宽度和深度，可将河网概化为一维问题。根据质量守恒和动量守恒定律，可建立描述河网水动力过程的一维圣维南方程组，如下所示：

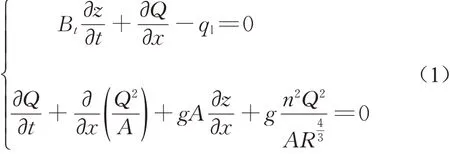
式中：z为河道水位；x为河道纵向距离；t为时间；Q为断面过流流量；A为横断面面积；Bt为河道横断面的非流动调蓄面积；ql为单位长度上的旁侧入流量，包括点源产生的污水排放量和降雨径流入河量，其中降雨径流入河量由栅格化降雨径流污染模型计算确定，如1.2节所述；g为重力加速度；R为河道横断面的水力半径；n为河道粗糙系数。

1.1.2 水质模型

河网水质模型控制方程由如下公式描述：

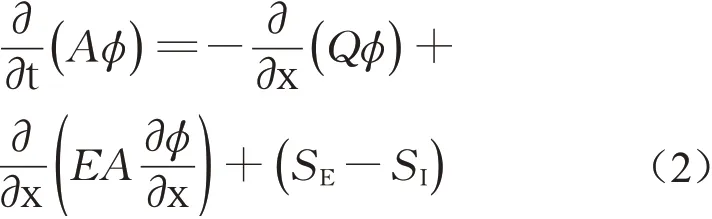
式中：φ为水质组分质量浓度；E为纵向离散系数；SE为点源和面源污染负荷排放汇入，其中面源污染负荷由栅格化面源模型计算确定，如1.2节所述；SI是描述水体中生物化学反应动力学过程，其作用机理架构如图1所示。

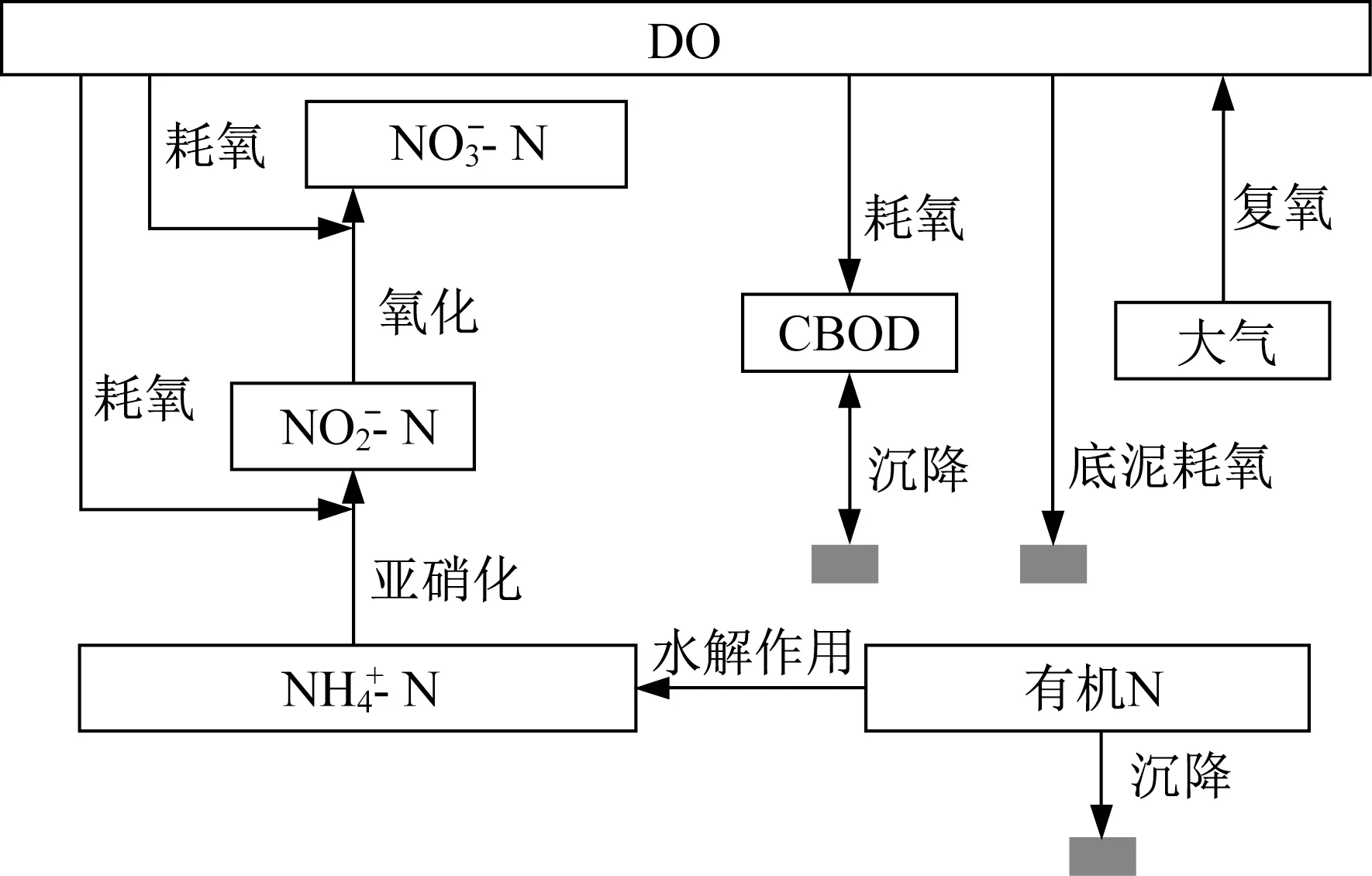
图1 水质模拟组分的耦合作用关系描述Fig.1 Description of coupling effect of components in water quality simulation

在图1中，水质模型描述了水体溶解氧平衡为核心的模型组分之间的相互作用关系。溶解氧的消耗考虑了含碳有机物生化降解耗氧和氨氮硝化作用耗氧以及河道底泥有机质分解耗氧；溶解氧的补充考虑了大气向水体中的复氧过程。其中氨氮的转化又涉及到氮的循环过程，即有机氮、氨氮、硝酸盐之间的转化。因此，水质模拟组分主要包括碳化BOD（CBOD）、有机氮、氨氮、硝酸盐和溶解氧及其之间的降解、转化速率等。

考虑到水动力和水质模型的开放性以及将来进一步建立智慧水务平台的需要，水动力和水质模型的模拟计算由开放式的模拟工具HEC-RAS模型系统（Hydrologic Engineering Center’s River Analysis System）实现［13-14］。在此基础上实现与自主开发的栅格化降雨径流污染模型的集成，满足河网地区水质动态模拟和水质动态达标分析的功能。

1.2 栅格化降雨径流污染模型

栅格化降雨径流污染模型以数字等高模型（Digital Elevation Model，DEM）为基础，自动提取水系和划分子流域，然后以子流域为基础计算降雨径流产流、产污量，并最终分配到对应的河道计算单元。模型的主要功能包括栅格降雨量插值计算提取、栅格径流深度计算、栅格径流污染物量计算和栅格水流汇流计算4个模块，计算思路如图2a所示。

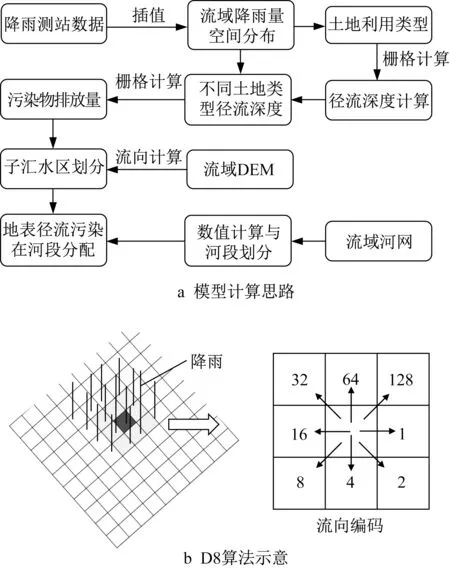
图2 栅格化降雨径流污染模型原理Fig.2 Principles of precipitation-runoff nonpoint pollution model based on DEM raster

（1）降雨量栅格分布计算。由于降雨量站点的实测数据仅为站点所处位置的降雨量，采用反向距离加权法（IDW）进行插值获得整个流域内每个栅格的降雨量［15］。

（2）降雨径流深度栅格分布计算。采用SCS曲线值法计算对应不同用地类型的栅格径流深度。SCS法为降雨径流关系法，能反映不同土壤类型、不同土地利用方式及前期土壤含水量对降雨径流的影响，具有参数少、简单易行等特点［16］。SCS曲线值法的方程为

其中

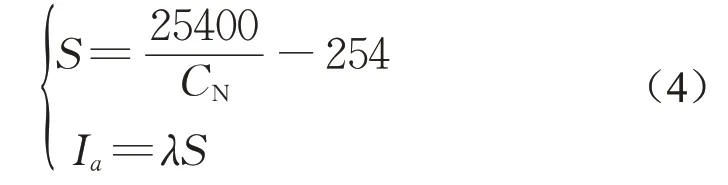
式中：S为潜在最大入渗量；P为一次降雨总量；Q为实际径流深；CN为该日的曲线值；Ia为由于地表储存、截留和下渗而导致的地表径流的初始损失量，与S呈一定的正比关系，通常可取λ为0.2。

（3）降雨径流污染物栅格分布计算。进一步，栅格像元上的降雨径流携带污染物量采用如下公式计算：

式中：L是栅格像元的污染物排放量；Cland为栅格像元的对应土地利用类型污染物径流质量浓度。

（4）栅格径流和污染物汇流计算。采用8点重力流向算法（deterministic eight-node，D8），基于数字地形高差进行汇流流向判断，自动提取水系，划分汇水区域［17］。为避免汇流过程模拟的失真，确定水流方向前需要进行DEM数据无凹陷处理。D8算法的基本思想是：在3×3窗口中，计算中心网格与邻域8个格网之间的距离权落差，具有最大权落差值的邻域格网方向即定义为水流方向，并且规定一个栅格单元的水流方向用一个特征码表示，如图2b所示。距离权落差计算公式如下：

式中：Δhi是中心栅格与邻域栅格的高程差值，栅格间的距离d与方向有关，在对角线方向为2倍栅格间距，在其他方向为1倍栅格间距。

根据流向计算结果分析每一栅格单元对应的上游汇水面积值。通过从上游到下游的汇水面积累加，建立河道计算单元与汇水面积的对应关系。结合栅格径流量和污染物计算结果，将降雨径流污染分配到对应的河道计算单元。

自主开发的降雨径流污染模型优势在于：①产流计算基于栅格式SCS模型，同时考虑了降雨和下垫面条件的空间不均匀性，具有空间尺度上计算精度高的特点；②产污计算基于输出系数模型，避免了面源污染形成机理的复杂性，所需参数少、操作简便。

2 模型的建立与率定

2.1 研究区域概况

武进地处长三角地理中心，位于常州、无锡及宜兴三市交界处。武进港是太湖梅梁湾的主要入湖河流之一，是连通京杭大运河和太湖的主要水上通道。武进港全长29 km，水深2～3 m，河宽25～30 m，流入太湖水量枯水年为2.72×108m3·a-1，丰水年为4.36×108m3·a-1。

本文将模型从武进港干流扩展到整个流域范围内的河网地区，研究区域土地利用类型以农业用地、居住用地、工业用地为主。概化河道包括武进港及武进港两岸采菱港、武南河、永安河、锡漂漕河、雅浦港5条主要河流，另外还有礼嘉大河、小留河、虎臣河、政平河、东阳岸河等28条支流。武进港及其流域概况如图3所示。

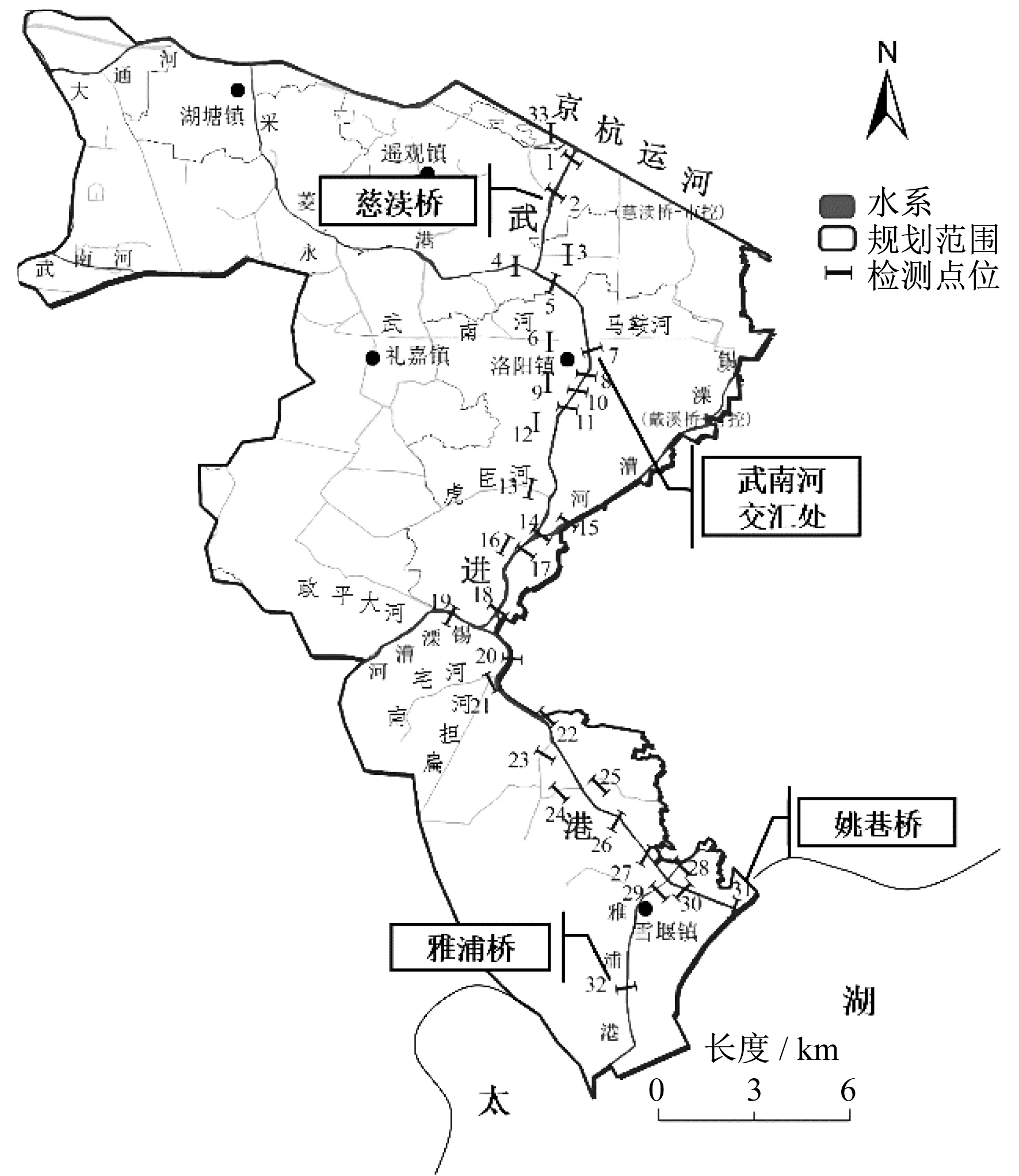
图3 研究区域概况Fig.3 Description of the site studied

2.2 模型边界条件

水动力模型上游和下游边界均采用水位过程线，数据来自坊前、常州、百渎口等水文站2018年日监测数据。

水质模型边界条件包括点源和面源污染负荷的输入，点源又可分为集中式点源和分散式点源。研究区域内集中式点源主要包括7座城镇污水处理厂尾水排放。分散式点源主要包括未经处理直排的农村生活污水和畜禽养殖废水，依据《太湖流域主要入湖河流水环境综合整治规划编制技术规范》［18］，采用排污系数法对分散式点源的化学需氧量（COD）、氨氮（NH3-N）、总氮（TN）、总磷（TP）负荷量进行估算，计算公式如下：

式中：W为分散式点源污染负荷量；Np为人口数；NL为畜禽养殖量；αp为农村生活污水排污系数，其中COD取27 g·人-1·d-1，NH3-N取4 g·人-1·d-1，TN取6 g·人-1·d-1，TP取0.2 g·人-1·d-1；αL为畜禽养殖排污系数，换算成生猪计算，COD取40.55 g·头-1·d-1，NH3-N取1.31 g·头-1·d-1，TN取3.05 g·头-1·d-1，TP取0.38 g·头-1·d-1；βP为农村生活污水入河系数，取0.7；βL为畜禽养殖入河系数，取0.6。

面源边界条件输入采用降雨径流污染模型的模拟结果，降雨径流污染模型中污染排放系数取值如表1所示。需要注意的是，污染负荷统计参数COD需与水质模型输入参数CBOD进行换算，换算系数依据经验取值：取5日生化需氧量BOD5与碳的生化需氧量CBOD的比值为0.70，BOD5与COD的比值为0.50，可 推 算 得CBOD与COD的 比 值为0.71［19］。

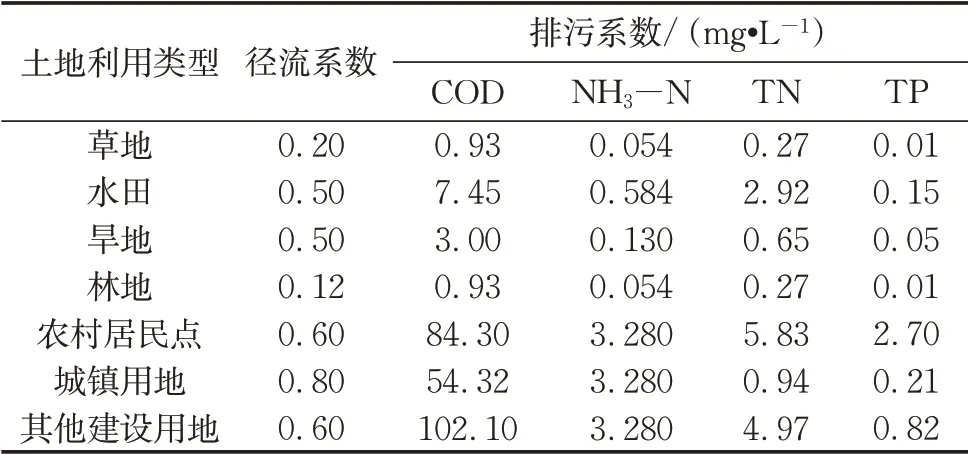
表1 研究区域不同土地利用类型径流面源污染输出系数Tab.1 Runoff nonpoint pollution export coefficients from different land use types in the catchments studied

计算得研究区域排放总流量为1.6×108t·a-1，COD、NH3-N、TN、TP污染负荷排放总量分别为9 024.1 t·a-1、621.4 t·a-1、1 275.8 t·a-1、80.8 t·a-1，图4给出了集中式点源、分散式点源和径流面源污染的负荷排放占比。可见虽然分散式点源排放流量很小，但排放污染负荷量占比却很高，COD、NH3-N、TN、TP占 比 分 别 为42.1%、46.3%、58.5%、45.2%。对于NH3-N，降雨径流污染占比也较高。

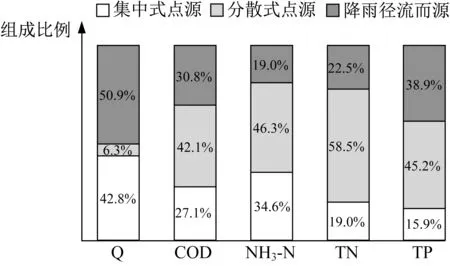
图4 研究区域各污染类型组成比例Fig.4 Discharge and proportion of each pollution type in the catchments studied

图5进一步展示了武进港流域以高精度DEM 5m分辨率栅格为单位的氨氮产生量以及不同河段的污染物空间分布，可以看出，雨季（8月）的降雨径流污染负荷入河量明显高于旱季（1月）。

2.3 模型率定验证

水质模型率定包括以下几个步骤：①输入上下游水动力边界及旁侧入流量，通过圣维南方程建立河道水动力模型；②输入点源和面源污染负荷以及各水质参数以模拟河道中水质的时空变化；③比较河道断面水质的实测值和模拟值，必要时调整水质参数。

分别采用纳什效率系数（Nash-Sutcliffe efficiency，NSE）和决定系数（R2）来评价水动力模型和水质模型质量的好坏，计算公式如下：

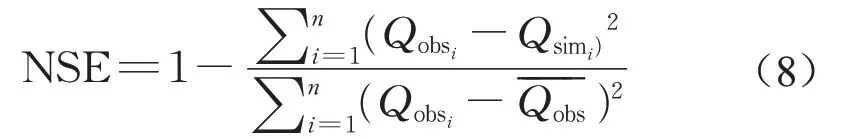
式中：Qsimi、Qobsi分别为日均流量模拟值和实测值；为日均流量实测值的平均值；n代表总共匹配的天数。NSE取值为负无穷至1，NSE越接近1，表示模型质量越好，模型可信度高。通常认为NSE达到0.75以上代表模拟结果很理想，NSE值在0.75～0.36之间模拟结果也是可以接受的，当NSE低于0.36代表模拟结果不理想［20］。

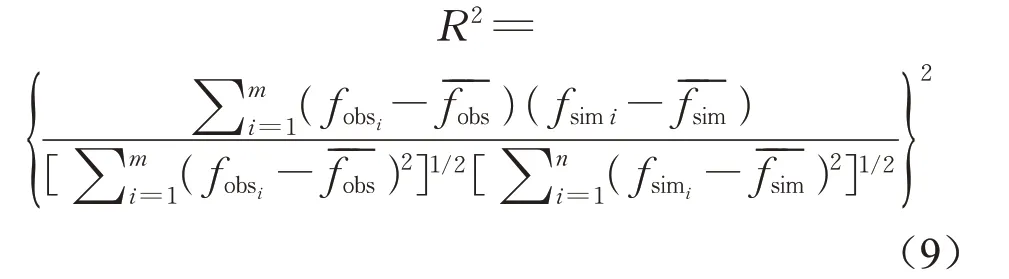
式中：fsimi、fobsi分别为月均水质浓度模拟值和月水质浓度实测值分别为月均水质浓度模拟值和实测值的平均值；m代表计算时间段内的月份数。R2取值为0至1，R2越接近1，表示模拟精度越好。通常认为R2大于0.6代表模拟结果理想，R2在0.6～0.5之间认为模拟结果总体上可以接受［21］。

研究区域河网水动力模型采用黄埝桥水文站2018年1—12月的日监测流量数据进行率定，如图6所示。可以看出，模拟值与实测值吻合情况较好，计算得NSE值为0.71，模拟误差在允许范围之内，率定后的河道粗糙系数取值为0.030～0.035。

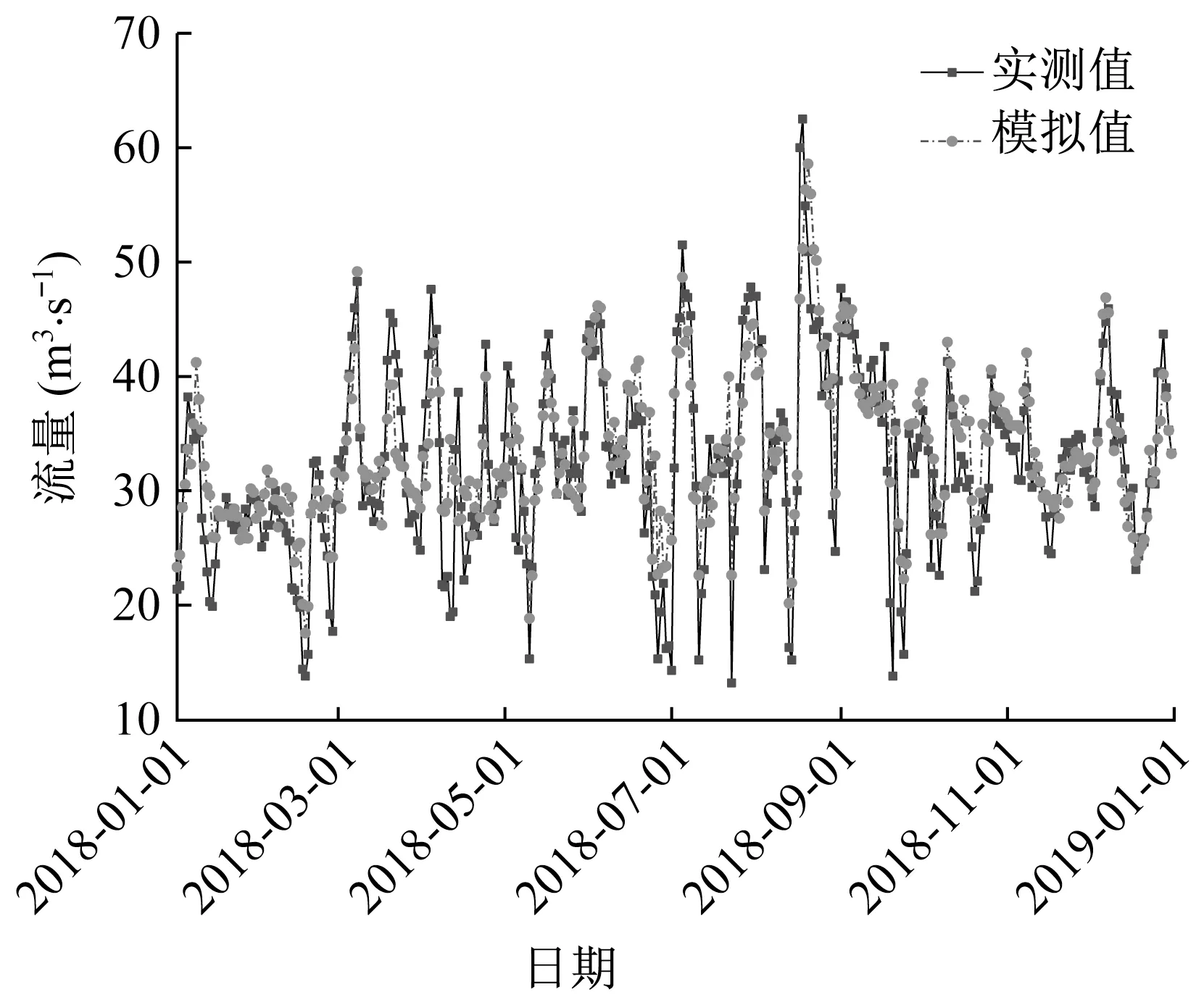
图6 黄埝桥断面流量率定结果Fig.6 Modeling calibration result for flow discharge at Huangnian Bridge station

水质模型采用武进港月采样监测数据（2018年4—12月），率定溶解氧（DO）、氨氮（NH3-N）、高锰酸盐（CODMn）和总磷（TP）4个水质指标，同样水质监测指标CODMn需与水质模型中的率定参数CBOD进行换算，取BOD5/CBOD=0.70、BOD5/CODMn=0.89，可推算得：CODMn/CBOD=0.79［22］。选取慈渎桥（CDQ2）和武南河下游（WN7）2个典型断面进行年尺度模拟。CDQ2断面位于武进港上游，主要污染源为上游客水，未受支流汇入污染影响；WN7断面位于武南河和武进港交汇处，水质受采菱港、武南河等汇入支流污染影响，总体而言水质差于CDQ2断面。由率定结果（图7）可以看出，模拟值与实测值吻合情况较好。依据式（9）计算得：①针对CDQ2断面，DO、NH3-N、CODMn和TP的R2值分别为0.82、0.69、0.61和0.71；②针对WN7断面，DO、NH3-N、CODMn和TP的R2值 分 别 为0.88、0.63、0.59和0.66，说明模拟误差均在允许范围之内，水质模型中主要参数率定结果如表2。率定结果显示，降雨强度较大时，受降雨径流汇入负荷的冲击，河道断面水质短时间内会出现急剧升高的现象，降雨结束后又恢复至常态。

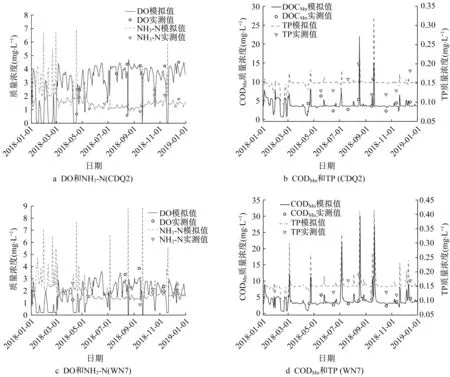
图7 CDQ2、WN7断面水质参数率定结果Fig.7 Calibration results of parameters for water quality modeling at CDQ2 and WN7 station

表2 水质模型主要参数率定结果Tab.2 Calibrated results of main parameters for water quality modeling

3 水质改善方案评估

3.1 污染削减方案比选

针对流域内分散点源占比高的特点，提出优先削减分散实点源污染排放，分析污染削减效果与入湖考核断面之间的水质响应关系。

由2.2节讨论可知，虽然分散式点源排放流量很小，但排放污染负荷量占比却最高。因此优化考虑农村分散式点源污染的削减方案，并评估污染削减前后的河道水质动态达标频次。

3.2 畜禽养殖污染控制

通过全面清理整顿非法和不符合规范标准的养殖场，进行养殖专业化，可实现畜禽养殖接近“零排放”。模拟研究片区内畜禽养殖全部关停或通过还田再利用实现畜禽污染零排河，即片区内畜禽养殖污染负荷削减率100%的情况下姚巷桥断面水质的响应情况，模拟结果见图8和表3。

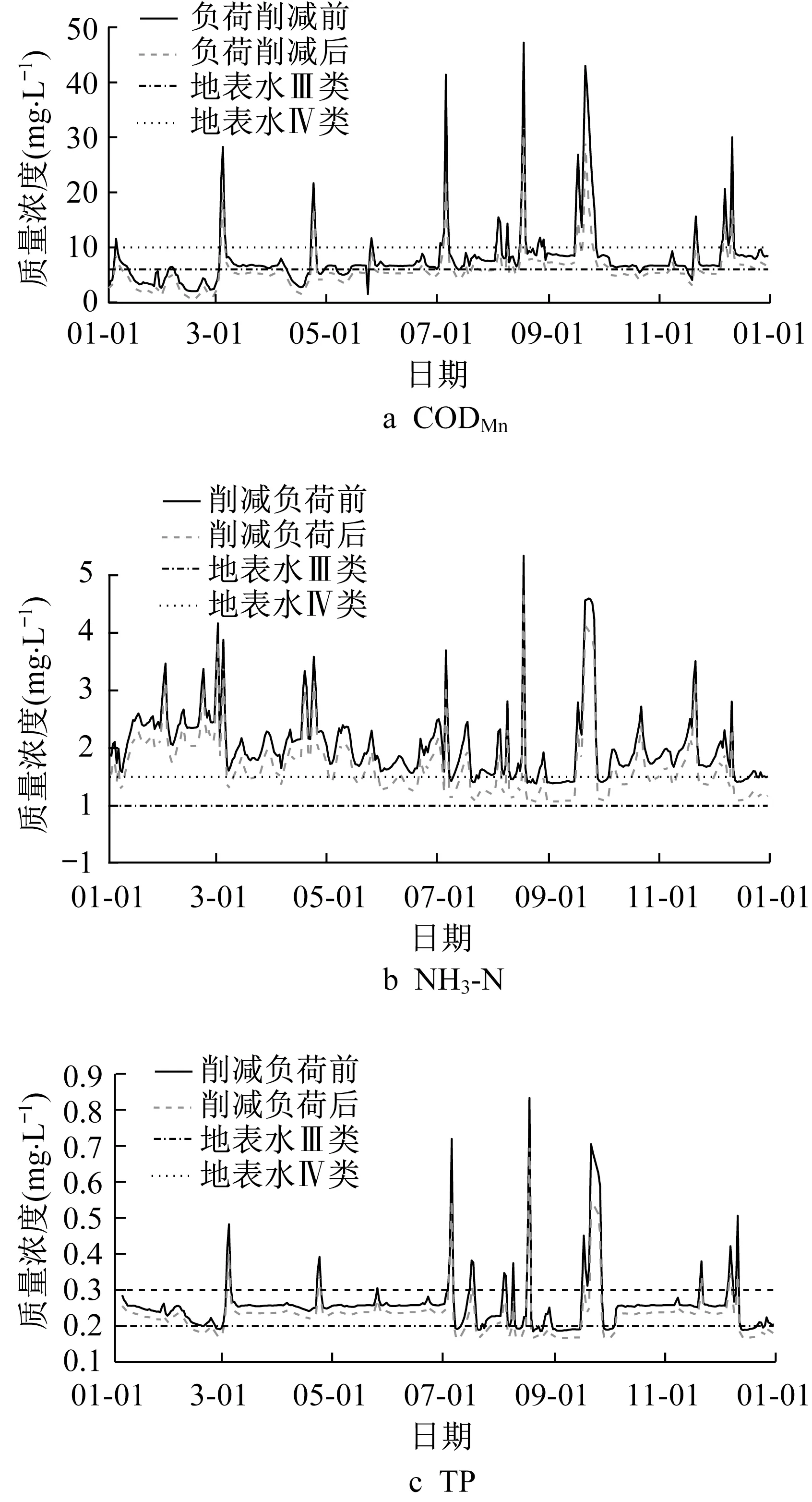
图8 畜禽养殖负荷削减前后入湖断面水质响应情况Fig.8 Predicted water quality at lake inflow station before and after livestock pollution reduction

削减畜禽养殖负荷后水质得到了一定程度的提升，特别是CODMn改善显著，年达标频次（地表水III类标准，简称III类）从23.0%提升至64.9%，但是NH3-N仍无法达标。

3.3 农村污水处理

收集未经处理的农村生活污水，经处理后以一级A标准排放。在畜禽养殖“零排放”基础上，结合流域内污染物空间分布特征，比选出对水质影响大的污染优先控制村落群，优先削减该村落群80%农村生活污水，以期进一步提高水质年达标频次。

共设计了3种污染优先控制村落比选方案：①工况1。选取片区内农村生活污水排放量最高的区域7个村落为污染优先控制村落，共削减COD 2 591.7t·a-1、NH3-N 120.4 t·a-1、TP 12.9 t·a-1；②工况2。在工况1的基础上，增加排入武进港干流的10个 村 落，共 削 减COD 3 330.4t·a-1、NH3-N 178.9 t·a-1、TP 30.3 t·a-1；③工况3。在工况1的基础上，增加排入上游来水京杭大运河的7个村落，共削 减COD 3 205.4 t·a-1、NH3-N 170.9 t·a-1、TP 29.1 t·a-1。分别模拟3种工况下姚巷桥断面水质的响应情况，模拟结果见图9和表3。

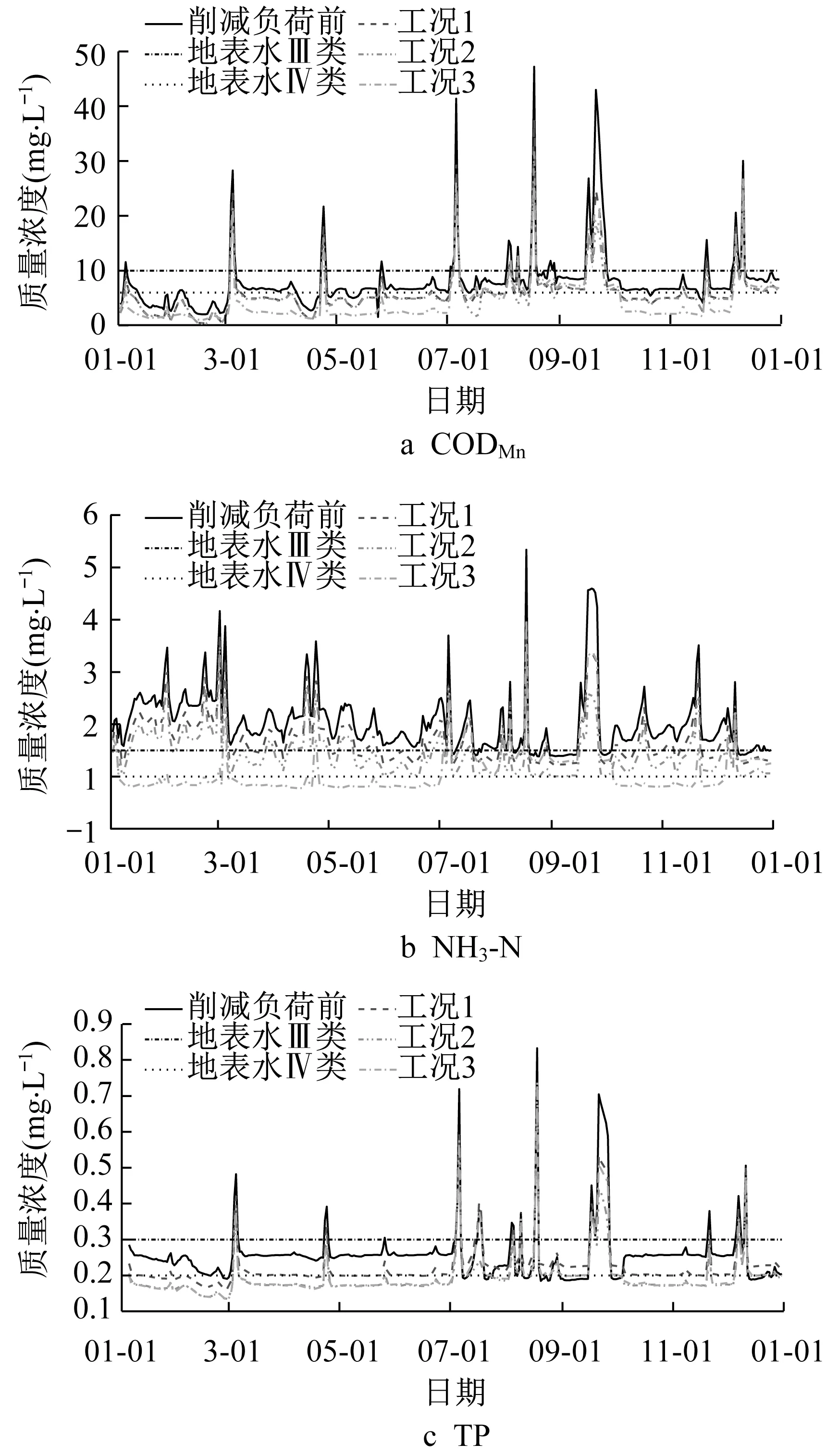
图9 不同农村污水削减工况下入湖断面水质响应情况Fig.9 Predicted water quality at lake inflow station of different rural sewage reduction schemes

表3 不同负荷削减工况下姚巷桥断面水质达标情况分析Tab.3 Annual attainment rates of NH3-N,CODMn,and TP at Yaoxiang Bridge station of different load reduction schemes

模拟结果可知，进一步削减污染优先控制村落相应农村生活污水后，姚巷桥断面水质得到明显改善。针对工况1，CODMn和TP改善效果较明显，CODMn年均值降至5.86 mg·L-1，年达天数（III类）从84 d提升至252d；TP的年均值降至0.22 mg·L-1，年达天数（III类）也从60 d提升至142 d，但是NH3-N仍无法达到地表水III类标准。工况2、3在工况1基础上分别削减排入武进港和京杭大运河村落群的入河负荷，针对CODMn和TP，工况2、3模拟结果相差不大；但是针对NH3-N，工况3的模拟结果明显优于工况2，NH3-N年均值降低至1.06 mg·L-1，年达标频次（III类）达66.3%，年达标天数（III类）达242 d。综上可得工况3为相对最优工况。

综上，改善客水水质、加强农村生活污水处理设施建设以及分散畜禽养殖污染治理可有效改善武进港水质；其中改善上游来水京杭大运河对提高姚巷桥断面年达标率效果尤为显著。相对最优工况下仍存在不达标天数主要是因为雨天受降雨径流汇入负荷的冲击，河道断面水质短时间内会出现急剧升高的现象。因此从水质动态达标的角度考虑，若要实现考核断面全面、稳定达标，需进一步加强对农田径流和地表径流污染的控制，如推进面源污染的河道生态拦截等工程措施，从而确保在雨后一段时间内能尽快恢复水质。

4 结论

建立了适用于河网小流域水环境系统模拟的水文—水动力—水质耦合数学模型，并在常州市武进港流域进行了实证研究。

（1）建立的耦合模型中，降雨径流污染模型采用自主开发的模型系统，以DEM栅格单元为基本模拟单位，可以对降雨径流导致的面源污染时空分布和汇流去向进行精准模拟。在此基础上，河道水动力水质模型采用开源模型HEC-RAS，构建了流域污染物排放与河道水质的响应关系，实现河网地区日尺度的水质模拟和动态预报。模型系统同时具有开放性，能够为小流域智慧监管平台提供技术支撑。

（2）针对武进港小流域分散式点源污染负荷高、部分汇入支流水质较差、长期难以达标的问题，将水动力水质模型从武进港干流扩展到整个流域范围内的河网地区，从而能够对武进港流域内的污染总量控制进行定量评估。结合流域内入河污染源组分和空间分布特点，模拟不同负荷削减工况下入湖考核断面姚巷桥的水质响应情况。从动态达标角度分析考虑，对不同水质方案进行评估。最优工况下，针对水质指标CODMn、NH3-N和TP，考核断面姚巷桥的年达标频次（III类）分别从23.0%、0、16.4%升高至71.8%、66.3%、75.9%。

作者贡献说明：

尹海龙：数学模型建立、论文撰写。

林夷媛：数学模型建立、论文撰写。

赵东华：技术和材料支持。

石泽敏：技术和材料支持。