考虑桩-土相互作用的高墩桥梁抗震性能

陈 旭，李春祥

（1.东北大学（日本）灾害科学国际研究所，仙台980-8576；2.上海大学力学与工程科学学院，上海200444）

随着近年来的经济发展，我国西部地区建设了大量的桥梁。为了跨越深山峡谷，这些桥梁的最大墩高往往超过40m，在某些极端情况下甚至会超过100m［1-2］。西部又是我国地震最为频发的地区之一，近20年内经历了例如汶川地震（2008年，M8.0）、玉树地震（2013年，M7.1）等重大灾害。考虑到上述这些高墩桥梁通常在当地的交通网络中处于枢纽地位，是震后救灾的生命线，因此需要对它们的抗震性能进行深入研究，确保其在震后能够迅速恢复一定的功能，允许应急车辆通过。

与常规中低墩桥梁不同，由于桥墩自身质量接近甚至大于上部结构，高墩桥梁的地震响应会受到墩身惯性力及高阶振型的显著影响［3］。现有关于高墩桥梁的数值分析及振动台实验研究表明，由于墩身高阶振型作用：①高墩墩身中部会在强震作用下产生第2个塑性铰，与现行规范假设不一致；②地震剪力及弯矩响应沿墩高的分布情况会比常规桥墩更加复杂，规范中的能力保护设计不再适用；③墩顶位移与墩底曲率不再同步变化，无法继续使用现行基于位移的方法进行抗震设计［4-6］。但上述这些研究，均未探讨土层特性及桩土相互作用对高墩桥梁地震响应的潜在影响，例如在振动台实验中，研究人员假设墩底固结，未考虑桩基础可能的破坏及对结构抗震性能的影响。

Chen等［7］在对高墩桥梁的研究过程中采用非线性p-y、t-z和q-z弹簧模拟了土层对桩基础的约束作用；并基于有限元分析结果指出，在强震作用下，土层确实会进入非线性状态，采用弹性弹簧（如m法）模拟基础刚度会对结果造成一定误差。但该项研究中，主要将土层作为桩基础的非线性约束，并未考虑其对地震动输入的影响，即未考虑地震波从基岩传递至地表的变化情况。

本文重点研究桩土相互作用对高墩桥梁地震响应的影响。首先基于OpenSees平台建立桥梁结构的非线性有限元模型，分别采用p-y等非线性弹簧和基于m法的线性弹簧对桩基础进行模拟。随后选取适当的地震动记录作为输入，通过对比不同工况的结果，分析土层对地震输入及结构响应的影响，并在此基础上，对实际工程的设计工作提出建议。

1 有限元模型及分析工况

1.1 原型介绍

选取如图1所示的西部地区典型高墩桥梁作为原型。该桥上部结构为4×30 m一联T型混凝土连续梁，位于高50 m的空心桥墩之上；墩梁之间采用10个GJZ 300×300×61叠层橡胶支座。每个桥墩横桥向宽度及截面壁厚沿墩高保持不变，分别为5.0 m和0.6 m；纵桥向墩顶宽度为2.1 m，沿墩高向底部按1/80倾斜度扩大，如图2所示。每个桥墩均位于由4根直径1.8 m、长30 m钢筋混凝土钻孔灌注桩支撑的承台上。

图1 桥梁原型立面（单位：m）Fig.1 Elevation of bridge prototype(unit:m)

1.2 数值模型

由于桥梁原型的质量及刚度分布较为均匀，因此为了简化分析过程、提高运算效率，研究过程中选取其中一个桥墩作为对象建模，如图1中阴影部分［6］。在现行抗震设计策略中，通常将上部结构（主梁及盖梁）作为能力保护构件，要求在地震中不发生破坏。因此建模时，将主梁简化为位于墩顶的质点，其质量等于一跨（30 m）主梁的质量（Ms），

采用弹性梁柱单元对盖梁进行模拟，如图3所示。从图1可以看出，纵桥向存在多个桥墩，因此模拟时限制墩顶质点绕横桥向的转动自由度；与之类似，由于梁底沿横桥向布置有多个桥墩，且盖梁设置有横向挡块，因而在简化模型中同样限制主梁绕纵桥向及竖向的转动自由度。亦即，图3中所示的墩顶质点，仅考虑沿纵桥向和横桥向的平动自由度，而不允许其发生转动。

由于桥墩在强震作用下会产生非线性反应，因此采用非线性纤维梁柱单元对其进行模拟。如图3c所示，根据材料及约束程度将截面细分为核心/保护层混凝土纤维和钢筋纤维。混凝土和钢筋材料的本构关系分别根据Kent-Scott-Park模型［8］和双折线模型［9］定义（如图4），混凝土本构关系参数中的下标cover和core分别对应保护层和核心混凝土。叠层橡胶支座采用如图4c所示的双折线模型进行模拟［7］；其中Gb、Ab和tr分别为橡胶层的剪切刚度、面积和总厚度，数值分别为1.0 MPa、9×104mm2和61 mm；其余参数可按图中公式计算。

图4 材料本构模型Fig.4 Constitutive relations of materials

1.3 桥梁基础模拟

如前所述，在Chen等［6］的振动台实验中，高墩模型直接固定于振动台上；而在实际工程中则通常基于m法，将土层和混凝土桩组成的基础等效为线弹性平动及转动弹簧，以提高运算效率。由于土体的非线性特性，这2种方向显然都无法考虑桩土相互作用，不能对桩基础进行准确模拟。而p-y曲线法是目前较为公认能够有效捕捉土体非线性性能的模拟方法［10-12］。在众多建立非线性p-y曲线的方法中，API（American Petroleum Institute）［13］方法是较为简单直接、应用广泛的一种。因此本文采用该方法，分别采用OpenSees软件中的PySimple1、TzSimple1和QzSimple1材料模拟非线性p-y、t-z和q-z弹簧，考虑土层效应。如图3a所示，这些非线性弹簧沿桩基础间隔2.0m分布。根据实际场地情况，计算相关弹簧参数时考虑3层土层，相应的内摩擦角分别为36°、40°和40°，m值分别取为1.2×104kN·m-4、1.5×104kN·m-4和2.5×104kN·m-4。此外，研究过程中还采用m法建立了线弹性空间6弹簧基础，以便与p-y弹簧模型进行对比，呈现桩土相互作用对高墩桥梁结构抗震性能的影响，如图3b所示。

1.4 分析工况

研究过程共考虑了如下3个工况：①工况1：考虑土层对于基岩地震动的影响，采用合适的地震记录作为输入加载于p-y弹簧模型，将所得到的结构反应作为比较基准；②工况2：直接将基岩地震动输入6弹簧模型；③工况3：将工况1中的地震动输入6弹簧模型。对比上述工况1和工况3的结果，可以明确采用6弹簧模拟桩基础体系的适用性；对比工况2和工况3的结果则可以获得基岩地震动经土层传递后对高墩结构地震响应的影响。

2 地震动选择及加载

2.1 地震动选择

为了避免地震动选择不当导致的结构反应偏差，Baker［14］提出了一种CMS-ε方法来选择合适的地震输入。这种方法通过采用ε刻画反应谱形状，同时根据场地条件确定目标反应谱（conditional mean spectrum，CMS），随后选择匹配该目标谱的地震动记录作为输入［15］。基于Lei等［16］对西部地区进行的地震灾害分析结果构建相应目标谱，并据此从太平洋地震工程研究中心（PEER）的强震数据库中选择了8条实际记录作为后续分析的地震动输入。

表1列出了所选地震动未经调幅的原始信息。从中可以看出，所有记录的震中距（Rjb）均小于10 km，地面加速度峰值（PGA）分布范围为0.190g至0.874g。图5给出了通过CMS-ε方法建立的目标谱以及所选择地震动的加速度反应谱。从图中可以看出，这8条地震动的平均加速度反应谱与目标谱非常吻合，表明这些地震记录能够有效表征西部地区的地震灾害情况。

图5 所选地震动加速度反应谱Fig.5 Acceleration spectra of selected motions

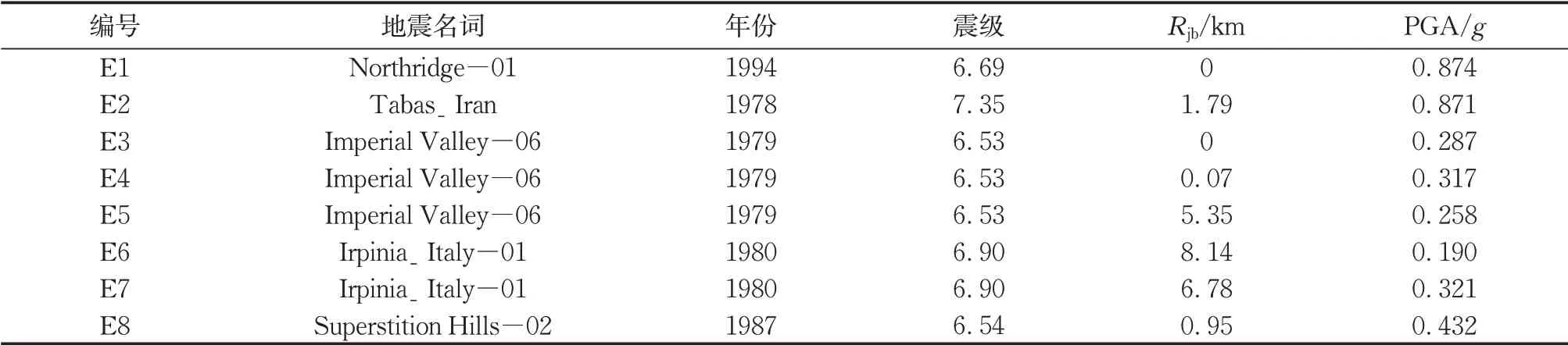
表1 所选地震动信息Tab.1 Selected input motions

2.2 地震动加载

为了充分考虑桩土相互作用对结构地震反应带来的影响，通常需要建立基岩及土层的半空间有限元模型，采用p-y弹簧模拟土层与桩基础的连接，随后将地震动施加于基岩底部进行时程分析。尽管这种方式所得到的结果相对较为精确，但会导致运算耗时过长［17］。Shang等［18］通过数值模拟及实验研究表明，将基岩传递至地表处的地震动作为一致输入，施加于桩基础节点处，可以获得较为精确的结构地震响应。因此为了简化有限元模型、提高分析效率，利用DEEPSOIL软件［19］考虑土层作用，获取地表处的地震反应，并将其作为动力分析时的输入（如图3所示）。图6以E1及E3地震动为例，对比了其在基岩和地表的时程，为便于比较，图中基岩地震动的峰值均已调整至1.0 m·s-2。从图中可以看出，在土层中传递之后，地震动的PGA都有所上升，E1、E3地震动从1.0 m·s-2分别上升至1.62 m·s-2、1.30 m·s-2；其余地震动的情况也与此类似。由此可见，若在分析过程中忽略土层的作用，可能导致结构输入地震动强度有所偏差，从而对分析结果造成显著影响。

图6 基岩地震动与地表地震动比较Fig.6 Comparisons of motions recorded at bedrock and ground surface

需要注意的是，尽管表1中所列出的地震动并非记录自基岩，但为了研究土层及桩土相互作用对高墩桥梁结构地震反应的影响，本文分析过程中将其视为基岩震动，在工况2中施加于基岩和承台底。而对于工况1和工况3，则将从DEEPSOIL软件中获得的地表地震动分别施加于各个非线性土弹簧节点和承台底部节点。

3 结果分析

采用增量动力分析（incremental dynamic analysis，IDA）方法对结构进行分析。首先根据目标反应谱选取实际地震动作为输入；随后将这些地震动从较小强度开始逐渐放大，在每一强度等级都对结构进行非线性时程分析；最后将所得到的结构响应与地震动强度呈现在同一张图上，研究结构的抗震性能［20］。

3.1 墩底内力响应

现有数值模拟及振动台试验研究表明，高墩桥梁的墩身最大剪力及弯矩需求通常仍然出现在墩底区域［5-6］，因此图7给出了3种工况下不同地震动输入强度时墩底剪力及弯矩的响应情况。图中空心标记表示不同地震动记录的结果，实心标记表示各工况的平均值。

从图7a中可以看出，当地震输入强度较小时（PGA小于0.8g），工况3的墩底剪力平均值与工况1较为接近，表明此时在实际工程中，可以将地表地震动输入该简化模型对高墩桥梁结构的地震响应进行分析。但随着地震强度不断上升，工况3得到的地震响应则会显著高于工况1；当PGA达到2.0g时，工况3模型的墩底剪力平均值分别比工况1偏大16.1%。这是由于较强的地震动会引起土体的非线性反应；而6弹簧模型则假设土体始终保持弹性，无法有效捕捉土-桩基体系由于非线性引起的刚度下降现象，从而高估了结构的地震内力反应。由于墩底剪力的大小还与能力保护设计中桩基础的受力需求密切相关，因此若此时采用工况3的结果进行实际设计，会对桩基础截面强度提出过高的要求，从而导致工程造价上升，降低经济效益。

另一方面，从工况2和工况3的结果可以看出，若忽略了土层导致的基岩与地表地震动差异，会始终低估墩底剪力需求，如果据此进行桥墩截面的抗剪设计，会得到偏于不安全的结果。并且较小的墩底剪力需求会导致较小的桩基础能力设计值，从而有可能导致桩基础在地震过程中发生破坏，无法实现基于能力保护理念的抗震设计。

需要注意的是，当地震动从基岩通过土层传递至地表时，其长周期成分基本保持不变，而短周期部分则有所放大。因此，上述不同工况下墩底剪力响应的差异与墩身的高阶振型效应密切相关。为了说明这一现象，图8以E1和E3地震动为例，给出了DEEPSOIL软件中基岩及地表地震动所对应的加速度反应谱。从图中可以看出，在长周期（T＞1.0 s）部分，2条地震动在基岩和地表处的反应谱基本重合；而在短周期部分，地表记录的加速度谱值则显著高于基岩记录。而既有研究表明，高墩墩身的剪力会受到高阶（尤其是2阶）振型的显著影响［4］。因此图7a中3种工况墩底剪力响应之间的差异主要是由高墩墩身高阶振型导致的。

图7b结果表明，3种工况的墩底弯矩反应基本保持一致；亦即如何模拟桩基础（工况1与工况3）、是否考虑土层的影响（工况2与工况3）对高墩底部弯矩响应的影响并不显著。出现这种现象的原因在于，墩底弯矩主要由一阶振型控制［4］；而图8表明，基岩和地表处地震动加速度反应谱在长周期部分的谱值几乎一致，因此墩底弯矩基本相同。

图7 不同工况下墩底内力响应Fig.7 Comparisons of internal forces at pier base

图8 基岩及地表处E1、E3地震动加速度反应谱Fig.8 Acceleration response spectra of E1 and E3 motion at bedrock and ground surface

为了更好地说明不同工况下墩身内力响应沿高度的分布情况，图9以E1地震动为例，分别给出了3种工况在PGA分别为0.8g和2.0g输入情况下的剪力和弯矩分布，图中各工况响应均以工况1底部响应值为基准进行了归一化处理。从图9a可见，地震动强度较小时（0.8g），工况1和工况3的剪力分布基本保持一致，显著高于工况2；而当PGA上升至2.0g后（图9c），尽管工况3在墩身中上部区域的剪力响应依然与工况1基本保持一致，但在墩底附近则明显偏大。该现象与图7a的情况相一致，即PGA较小时采用地表地震动输入6弹簧模型，能够有效模拟高墩结构的剪力响应，而在PGA较大时，则会导致较大的误差。另一方面，不同工况下弯矩响应（图9b和9d）的差异则明显小于剪力响应；尤其在墩底区域内，3种工况所得到的结果基本保持一致。

图9 E1地震动下不同工况墩身内力分布Fig.9 Seismic internal forces of pier column under E1 motion

3.2 承台地震响应

桩基础通常埋置于地表以下，一旦在地震中发生破坏，难以检查和修复。因此在目前的桥梁抗震设计方法中，均将桩基础作为能力保护构件，要求其在地震作用下保持弹性、不发生损伤。相关研究表明，承台质心位置处的位移是一种能够有效表征桩基础震后性能的损伤指标［21］。根据Chen等［7］的工作，对于本文中所选用的高墩桥梁，当承台质心位移达到1.30 cm时，桩基础中的纵向钢筋即会发生屈服；而当质心位移达到5.17 cm时，桩基中的纵筋会拉断，导致完全破坏。

图10中给出了在不同强度输入情况下3种工况承台质心的最大位移响应。从中可以看出，当采用6弹簧模型模拟基础时（工况2及工况3），不论采用何种地震动输入，都会极大低估承台质心处的位移反应，从而低估桩基础可能出现的损伤。以平均值为例，p-y模型（工况1）表明当输入地震动PGA大于0.8g时，桩基础就会发生屈服，出现一定程度的损伤；但根据工况2的结果，桩基础则始终会保持弹性，而工况3也只有当PGA上升至1.8g时，桩基础才会出现一定的非线性反应。这些现象表明，采用基于线性假设的6弹簧模型，对于高墩桥梁的桩基础抗震设计是一种偏于不安全的方法。

图10 不同工况下承台质心位移Fig.10 Comparisons of displacement at centroid of pile cap

4 结论

分别采用p-y、t-z、q-z非线性弹簧和基于m法的线性弹簧对桩基础进行了模拟，通过对比采用这2种基础的有限元模型分析结果，研究了桩土相互作用对高墩桥梁地震性能的影响。研究结果表明，当地震动强度较小时，将基岩传递至地表的地震动输入6弹簧模型，能够得到较为精确的墩身剪力需求响应；但随着地震动强度上升，6弹簧模型无法捕捉土层的非线性反应，从而会高估墩身的剪力需求。另一方面，墩身弯矩则可以通过6弹簧模型进行较好的估计。由于地震动从基岩传递至地表时，长周期成分（T＞1.0 s）基本保持不变，而短周期成分会发生明显变化。因此高墩墩身的高阶振型效应是导致上述现象出现的主要原因。

但是，6弹簧模型始终会极大低估承台质心的地震位移响应，这意味着利用这种模型对高墩桥梁桩基础进行设计，会得到偏于不安全的结果。需要注意的是，这一点对于常规中低墩桥梁的抗震设计并不关键，因为这类桥墩桩基的安全性可以通过能力保护设计得到保证。但是在高墩桥梁中，由于能力保护设计策略失效，因此必须要通过承台位移来判断桩基础的损伤状况，这就要求设计人员在实际工程中对此特别加以注意。

综上所述，在实际工程中对高墩桥梁进行较小地震下的设计时，采用地表地震动记录作为输入，利用6弹簧模型可以得到较为精确的墩身剪力和弯矩需求；随着地震强度的上升，该方法依然能够较好估计弯矩需求，但会高估剪力需求。而当要对桩基础进行设计时，则不可采用6弹簧模型，否则会得到偏于不安全的结果。

作者贡献说明：

陈旭：构思框架，构建模型，处理数据，撰写、修改文稿。

李春祥：构思框架，修改、确定文稿。