沉管隧道多尺度方法与地震响应分析
禹海涛,宋 毅,李亚东,张劭华,徐 磊
(1.同济大学岩土及地下工程教育部重点实验室,上海200092;2.同济大学土木工程学院,上海200092;3.广州大学土木工程学院,广东广州510006;4.上海建工一建集团有限公司,上海200120)
沉管隧道作为一种连接城市交通网络的水下隧道,自20世纪90年代首次在我国应用以来,日益受到重视并广泛应用于沿江沿海城市。因其既有一般地下结构的地震反应特点[1],又有饱和软弱地层不均匀沉降、上覆土约束作用小等特殊性[2],一旦破坏则难以修复,且可能产生灾难性的后果。因此,对沉管隧道进行抗震安全性研究是十分必要的。
目前沉管隧道抗震分析主要借助于动力有限元方法,但由于沉管隧道尺度较大且接头构造复杂,针对沉管隧道地震响应分析的三维全精细化模型的研究仍然较少。丁峻宏等[3]基于显式有限元和高性能计算平台,建立了包括地基土、沉管隧道以及柔性接头在内的三维全精细化分析模型,进行了大规模地震响应仿真分析,但其计算量过于庞大,对于长度显著的沉管隧道适用性较差,且不便于指导工程设计。因此,简化分析模型的提出及改进成为当前学者们关注的热点。
梁-弹簧模型是隧道纵向地震响应分析广泛采用的简化模型,以此为基础发展而来的不同地基及任意动载下长隧道纵向动力响应解析解[4-5]对于隧道抗震设计具有重要的应用价值。笔者[6]曾基于黏弹性地基梁理论,结合精细化接头模型,提出了一种模拟盾构隧道纵向地震响应的多尺度分析方法,并成功应用于工程实际。而针对沉管隧道结构特点,日本学者田村重四郎和冈本舜三等[7]基于振动台模型试验和地震观测,提出了一种基于土质点-弹簧模型的沉管隧道地震响应分析方法,该计算模型成功应用于日本东京湾沉管隧道的抗震设计,且至今仍得到广泛应用[8]。严松宏等[9]应用该模型对南京长江隧道沉管段进行了纵向地震响应分析。然而,该质点-弹簧模型基于单质点体系一阶振动模态的假定,对于复杂场地,尤其是分层土场地响应的模拟精度较差。基于模态等效方法,Li等[10-11]建立了适用于二维黏弹性场地反应分析的等效多自由度体系,克服了质点-弹簧模型精度不够的问题。
总体而言,目前对于沉管隧道简化模型及改进方法的研究仅能反映隧道整体的宏观响应,但无法合理模拟接头细部构造特征。沉管接头作为连接管节的关键节点,由于相对管节本体而言刚度较低,从而成为制约沉管隧道抗震设计的薄弱环节[12],因此接头细部构造的合理模拟应是沉管隧道抗震分析的关键[13]。
本文建立沉管隧道地震响应分析的多尺度模型,同时考虑沉管隧道宏观整体响应特征和接头细观构造特点,并将该模型应用于广州市某在建沉管隧道工程,研究沉管隧道管节及接头的抗震性能,并揭示地震动输入方向、环境温度变化等因素对于沉管隧道地震响应的影响规律。
1 多尺度方法
1.1 多尺度模型
针对目前简化模型无法反映沉管隧道接头细部构造的不足,提出了沉管隧道地震响应分析的多尺度方法,其中宏观多质点-弹簧-梁耦合模型用于描述沉管隧道结构与地层的动力相互作用及隧道整体地震响应特征,细观精细化模型用于捕捉沉管接头的张合量、剪力键受力等动态演化规律,如图1所示。
1.1.1 隧道整体宏观模型
本文提出的多尺度方法中,宏观模型采用多质点-弹簧-梁模型[7],其假定地层的自振特性不受隧道存在的影响。而由于隧道尺度与整个场地范围相比很小,隧道存在对整个场地的基频基本没有影响,但对于隧道周边局部范围仍具有一定局限性[14]。但考虑到局部相互作用的复杂性以及研究的重点,本文简化方法仍遵循这一假定。此外隧道的地震响应主要受地层的基本剪切振型控制,且忽略隧道自身惯性力对其动态响应的影响,这一点已被以往的大量研究所证实[1]。
将地层沿隧道纵向划分成一系列垂直于隧道轴线的切片单元,每一切片单元简化成与其具有等效自振周期的单质点-弹簧体系,然后将相邻土质点之间用弹簧连接,从而构成多质点-弹簧模型;将隧道管节简化为梁单元,并通过弹簧和阻尼元件与周围地层相连,即形成隧道整体宏观模型,如图1所示。图中,Mk、K3和C3分别为等效单质点-弹簧体系的土质点质量、弹簧刚度和阻尼系数;K2为相邻土质点之间的连接弹簧刚度;K1和C1分别为土与隧道之间相互作用的弹簧刚度和阻尼系数。

图1 沉管隧道多尺度模型Fig.1 Multi-scale model of immersed tunnel
1.1.2 接头细观精细化模型
在传统的沉管隧道多质点-弹簧-梁模型中,管节接头采用不同自由度的线性弹簧单元模拟。然而,一方面,实际管节接头广泛采用柔性橡胶止水带,且由于橡胶为超弹性材料,接头刚度将随受力而发生变化;另一方面,管节接头构造复杂,布置有多组水平和竖向剪力键,因此采用传统方法很难真实地模拟管节接头的力学性能。
为此,依据管节接头的细部设计构造及其受力特征(图2a),建立沉管接头细观精细化力学模型,如图2b所示。沿管节端面GINA橡胶止水带的中心线,每隔1m设置一个非线性弹簧单元来模拟GINA止水带的受力和变形;根据接头水平和竖向剪力键的实际位置,采用多折线弹簧单元来模拟剪力键的受力和变形。各弹簧节点与相邻管节端点刚性连接,即形成接头细观精细化模型。其中,各弹簧单元方向的定义与图1中的整体坐标系一致,GINA止水带仅产生轴向受力和变形,相应弹簧单元方向为轴向,即x方向;水平和竖向剪力键的弹簧单元方向则分别为y方向和z方向。

图2 沉管接头详图Fig.2 Details of immersion joint
1.1.3 多尺度耦合关系
为保证不同尺度模型间的位移协调,需要建立相应的多尺度耦合关系。以接头处梁端点O1为原点,建立随管节梁单元变形而运动的动态局部坐标系,其x方向始终指向管节轴向,如图2b所示。设相应接头弹簧端点为Si,由于隧道宏观模型与接头细观模型在轴向上需满足位移协调条件,且考虑到接头弹簧节点为均匀对称分布,因此有

式中:x′O1、x′si分别为O1点和Si点的局部x轴坐标。
此外,隧道宏观模型与接头细观模型还应在横断面方向上保持位移协调,即

式中:y′O1、z′O1分别为O1点的y轴和z轴局部坐标;y′si、z′si分别为Si点的y轴和z轴局部坐标;j为接头弹簧单元数量。
1.2 地层弹簧刚度和阻尼系数
1.2.1 等效单质点-弹簧体系
等效单质点-弹簧体系的土质点质量等于土切片单元的一阶振型有效质量。单位长度土切片的一阶振型有效质量Me按式(3)计算:

式中:mi为第i层土的质量;φi为第i层土的一阶剪切振型;n为土层层数。
第k个土质点的质量Mk等于单位长度土切片的一阶振型有效质量Me与土切片长度Lk的乘积,即

假定地层为均质各向同性的半无限介质,则土切片单元的2个水平方向(x向和y向)模态振型一致,因此相应等效单质点-弹簧体系的刚度系数K3x和K3y相同,均可由土切片单元的一阶振动周期来计算,即

式中:Tk和ωk分别为第k个土切片单元一阶剪切振动的周期和频率。
竖向弹簧刚度系数K3z可按式(6)计算:

式中:ν为土体泊松比。
1.2.2 相邻土质点之间的连接弹簧
土质点之间的水平纵向拉压弹簧刚度系数K2x、水平横向和竖向剪切弹簧刚度系数K2y和K2z,可依据相邻质点产生相应方向的单位相对位移所需的作用力得到,如图3所示。由一阶振型分析求出各土层振型位移,再由各土层剪切模量计算产生单位相对位移所需的力,即
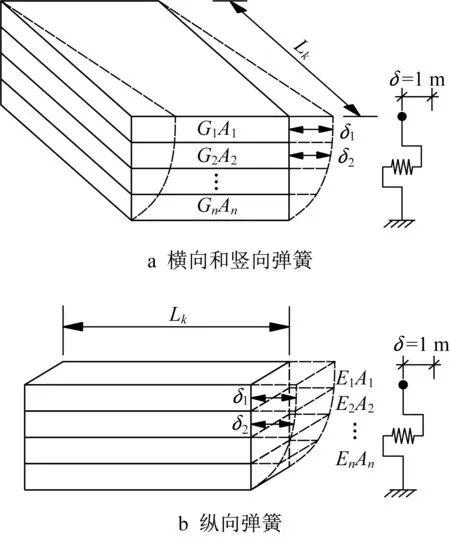
图3 相邻土质点之间的弹簧刚度[15]Fig.3 Spring stiffness between adjacent soil particles[15]

式中:Gi和Ei分别为第i层土的剪切模量和弹性模量;Ai为第i层土的截面面积;δi为第i层土的振型位移。
1.2.3 土-结构相互作用弹簧
土和沉管隧道结构之间相互作用的弹簧刚度K1等于作用在隧道处的力P与它所引起的位移δ之商,即

1.2.4 阻尼系数
等效单质点-弹簧体系的阻尼系数可由土切片单元的一阶振动频率来计算
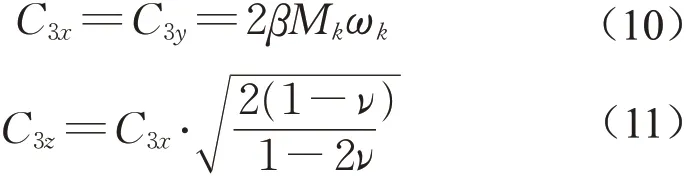
式中:β为阻尼比,取0.05。
均质半空间中任意形状埋置基础的阻尼系数按式(12)计算[16]:

式中:ρ为土体密度;Vs为土体剪切波速;b为基础的半宽;d为地表到基础侧墙与土体的有效接触深度;Aw为基础侧墙与土体的有效接触面积;C1x,sur、C1y,sur、C1z,sur分别为相同形状表置基础的阻尼系数,可按式(13)计算[16]:

式中:Ab为基础底面面积;和分别为水平横向和竖向阻尼系数修正系数;VLa为Lysmer类波速,按式(14)计算[16]:

2 工程应用
2.1 分析模型及参数
以广州某沉管隧道工程为背景,采用ABAQUS有限元软件建立多尺度模型进行抗震分析。该隧道由6管节组成,每管节长度103 m,为模拟暗埋段影响,模型两端计算边界各取100 m,模型总长818 m。隧道管节采用三维梁单元模拟,每个管节划分为20个单元。隧道管节结构横断面为两孔一管廊设计,如图2a,外包尺寸为宽30.4 m、高9.5 m。管节接头设置GINA止水带、2组水平向剪力键及4组竖向剪力键。模型接头采用如1.1节所述的细观精细化建模,其中,GINA止水带由84个非线性弹簧单元模拟,每组剪力键则在相应位置处设置一个多折线弹簧单元。沉管隧道多尺度有限元模型如图4所示,图中E1~E6表示沉管管节编号。

图4 有限元模型Fig.4 Finite element model
为了充分考虑纵向地基的不均匀性,如图4所示,考虑管节长度并参考场地钻孔位置,沿隧道纵向将土层划分为6个区段,分别建立土切片的等效单自由度体系。在相邻区段土层的等效单自由度体系之间,每隔10m左右进行插值,并通过纵向弹簧单元连接对应土质点,从而形成场地地震动特性模拟的多质点-弹簧模型。
场地土层参数如表1所示。利用各区段的土层分层情况及动力参数分别建立相应的土层切片模型进行振型分析,从而得到隧道沿线场地主频和土体一阶振型质量,根据前述公式计算不同区段等效单自由度体系的弹簧刚度和阻尼系数以及各连接弹簧参数,最终得到隧道宏观模型各弹簧刚度和阻尼系数如表2所示。

表1 土的密度和剪切波速动力参数汇总Tab.1 Dynamic parameters of soil density and shear wave velocity

表2 隧道宏观模型弹簧、阻尼系数Tab.2 Spring and damping coefficient of macroscopic model of tunnel
管节接头构件的实测荷载-变形曲线如图5所示。为验证应用实例中细观模型及参数的正确性,按照前述方法建立相应的接头细观力学模型,并进行轴向压缩和水平剪切荷载作用下的数值模拟。从图中可以看出,模拟结果与实测数据基本一致,表明所建立的细观力学模型可以准确模拟接头的实际力学行为。

图5 接头细观模型荷载-变形曲线Fig.5 Load-deformation curve of joint microscopic model
2.2 计算流程
为了真实模拟沉管隧道初始受力状态,计算分析中考虑了沉管隧道施工期水力压接的全过程以及重力荷载条件下的隧道受力和接头变形状态,在此基础上进行隧道的地震响应模拟。此外,鉴于隧道周围环境温度会随季节发生变化,因此计算工况综合考虑了整体升温或整体降温分析步,以研究环境温度变化对隧道动力响应的影响机制。具体计算流程如图6所示。

图6 计算流程Fig.6 Flowchart of calculation
依据工程场地地震安全性评价报告,选取设防烈度下50年超越概率为10%的人工地震动时程作为基岩面输入,如图7所示。
图7 输入地震动时程Fig.7 Input time history of ground motion
本文重点分析地震动输入方向、隧道整体温度变化对隧道动力响应的影响。计算工况如表3,其中,Static表示仅包含水力压接及重力分析步的初始静力工况;SV波振动方向与隧道轴线夹角成0°、45°、90°输入,分别用L、TL、T表示;整体升温、整体降温分别用S、J表示。为了便于后续结果对比分析,以工况1即地震动沿纵向0°输入作为标准工况。

表3 计算工况Tab.3 Conditions of calculation
3 地震响应分析
3.1 标准工况(L)结果分析
标准工况下地震动沿纵向0°输入,隧道宏观模型的响应主要分析隧道的最大轴力,如图8a所示。图中,初始值代表初始静力工况Static的隧道内力,相应工况则表示叠加输入地震动后的总体响应。由图可见,在初始静力状态下,受水力压接作用影响,隧道整体处于受压状态,且由于水深变化,隧道中部受压较大,并向两端递减。输入地震动后,轴力增幅明显,且由于纵向地基的不均匀性,各管节最大轴力有一定差异。峰值出现在E1管节,约3.7×105kN,达到该点初始状态的19倍,其相应时程如图9a所示,图中静力分析步表示地震荷载施加之前的各分析步长,已在相应曲线段标明。
接头细观模型的响应则重点关注相对初始静力工况的接头张合量。由于管节接头是由一系列非线性弹簧单元构成的模拟元件,各弹簧节点与相邻管节端点刚性连接,其接头某一刻的张合变形模式是以接头梁端点为中心对称分布,因此提取各接头张合量峰值点数据,以包络图形式来表征各接头的相对变形,如图8b所示。其中,接头相对张合量以相对张开为正、相对压缩为负。从图中可以看出,地震作用下各管节接头相对变形范围随场地条件变化而有所差异,峰值接近60 mm。提取该接头压缩量时程如图9b,初始静力工况下,接头压缩量约130 mm,并在地震作用下,其相对变形在60 mm以内变化。

图8 标准工况下隧道响应Fig.8 Response of tunnel under standard calculation condition
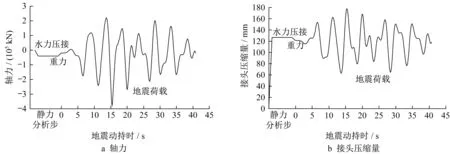
图9 标准工况下响应峰值点时程Fig.9 Time history of peak point under standard calculation condition
3.2 地震动输入方向影响分析
地震动沿与隧道轴线不同夹角输入时,隧道宏观模型的响应以隧道最大轴力和最大水平弯矩为分析指标,如图10所示。隧道轴力在纵向0°输入时为最不利状态。随着输入方向与隧道轴向夹角的增加,地震动引起的结构轴向作用分量逐渐减小,隧道最大轴力明显减小,90°输入时峰值仅为0.7×105kN;而水平横向作用分量则逐渐增加,隧道弯矩也随之增大,并在90°输入时达到最大值,峰值点出现在E6管节,约为3.2×105kN·m。

图10 不同地震动输入方向下隧道整体响应Fig.10 Response of tunnel in different ground motion input directions
接头细观模型的响应重点研究接头相对张合量与水平剪力键剪力,如图11所示。地震动沿纵向0°输入时,接头相对张合量达到最大值。随着输入方向与隧道轴向夹角的增加,隧道轴向作用力减小,接头相对张合量均随之减小,90°输入时最大张合量在10 mm以内;接头水平剪力则随着水平横向作用力的增加而显著增大,并以90°输入时为最不利状态,峰值约4.8×104kN。

图11 不同地震动输入方向下接头响应Fig.11 Response of joint in different ground motion input directions
3.3 整体温度变化影响分析
本节进一步分析环境温度变化对隧道地震响应的影响。地震动沿纵向0°输入,隧道宏观模型的响应主要分析隧道的最大轴力,如图12a所示。图中,Static-S(Static-J)表示在初始静力工况基础上整体升温(降温)分析步后的结果。可见,整体升温后,静力工况及地震作用下的隧道轴力均有所增加,而整体降温后,隧道最大轴力均为拉力,地震作用下峰值达到3.2×105kN,在设计时应注意接头及温度缝的处理。提取该点轴力时程如图13a所示,从图中可以看出,整体升温导致管节膨胀,从而增大了隧道轴力,而降温则引起管节收缩,导致管节由初始受压状态转变为受拉状态,地震作用则在此基础上进一步放大了隧道的张拉受力效应。

图12 温度变化下隧道响应Fig.12 Response of tunnel to temperature change
接头细观模型的响应主要分析接头相对张合量。如图12b所示,升温后管节膨胀导致接头压缩,降温后管节收缩则会引起接头较大程度的张开,而在地震作用下最大张开量已超过80 mm。可见,相比于静力工况下的升温或降温,地震作用仍是接头产生相对变形的主导因素。相应的温度变化作用下接头压缩量时程如图13b所示。

图13 温度变化下响应峰值点时程Fig.13 Time history of peak point of response to temperature change
4 结论
提出了一种用于沉管隧道纵向地震响应分析的多尺度方法,即在宏观多质点-弹簧-梁模型的基础上,建立管节接头的细观力学模型,可以同时反映隧道宏观整体响应和接头细观响应特点。采用该方法对广州某沉管隧道进行了抗震分析,并综合考虑地震动输入方向、整体温度变化等因素的影响,得出以下结论:
(1)相比于静力工况,地震作用会显著放大隧道内力,并使接头出现较大幅度的相对变形。
(2)当地震动输入方向与隧道轴向夹角为0°时,隧道轴力与接头变形达到峰值;随着地震动输入方向与隧道轴向夹角的增加,隧道弯矩及接头剪力逐渐增加,并在90°输入时达到峰值,增幅达到了4个数量级,而隧道轴力及接头变形则随之减小。其中,峰值轴力的降幅超过了85%,仅为0.7×105kN,90°输入时的接头最大张合量则在10mm以内,仅为0°输入时的17%。
(3)隧道轴力及接头变形受环境温度变化影响显著。升温使管节轴力增大而接头相对张开量减小,而降温不仅使得接头相对张开量增加了约30%,还会导致管节出现较大的拉力,且已接近峰值轴力的60%,因此在实际沉管隧道结构设计中应予以重视。
作者贡献说明:
禹海涛:项目负责人、论文构思、指导模型构建及数据分析,论文修改。
宋毅:模型构建、数据分析呈现及论文撰写。
李亚东:项目负责人、资料提供及分析指导。
张劭华:指导模型构建及数据分析。
徐磊:项目联络与沟通、提供项目资料。

