地下结构抗震分析反应谱法与现有简化方法对比
赵 密,李 苗,昝子卉,高志懂,杜修力,王君杰
(1.北京工业大学城市与工程安全减灾教育部重点实验室,北京100124;2.广州地铁设计研究院股份有限公司,广东 广州510000;3.同济大学土木工程学院,上海200092)
由于地下结构受到周围土体的约束,初期人们认为地下结构地震安全性远高于地上结构,地下结构抗震问题没有引起人们的重视。近年来,世界范围内发生了多次地下结构震害事例,包括1995年日本神户地震、1999年中国台湾集集地震、1999年土耳其科贾埃里地震以及2008年中国汶川地震等。日本神户大地震中[1],地铁区间隧道及地铁车站遭受了严重破坏,甚至出现大开地铁车站完全塌毁的震害实例[2],地下结构抗震问题受到关注,进行地下结构抗震设计成为共识。研究地下结构抗震分析方法对建立和完善规范法规并指导工程设计具有重要意义。
为了考虑土-结构相互作用,认为地下结构所受地震荷载包括结构顶底板间相对位移峰值时刻的土体位移、土体剪力和惯性力三部分,提出了反应位移法[3],并已被纳入我国多部抗震设计规范[4-7]。该方法在结构周围施加土体弹簧,弹簧系数难于精确确定,导致结构反应误差较大[8-12]。为了更为准确地考虑土-结构相互作用,建立结构及其附近部分土体的整体分析模型,将一维场地反应计算的有效加速度以体力方式施加于整体模型,提出了反应加速度法[13],并已被纳入我国《城市轨道交通结构抗震设计规范:GB 50909—2014》[7]。
近年来,关于反应位移法和反应加速度法的精度对比以及2种方法的改进研究取得了一些成果。许紫刚等[14]通过算例对比了常见的地下结构抗震简化分析方法。针对各分析方法的计算模型、关键参数、优缺点以及存在的问题进行了较为系统的评述,并与严格的动力时程分析方法结果进行了比较,分析了各种方法的计算精度,可为进一步发展和完善现有的地下结构抗震简化分析方法提供参考。吴敏[15]以上海市临港综合区浩通路综合管廊结构为例,对比反应位移法和反应加速度法的计算效果。研究表明:相对于反应位移法,反应加速度法的计算过程更为简便,计算结果更为精确。陶连金等[16]选取拱形断面地下结构,以时程分析方法为参考,对比反应加速度法和反应位移法的精度,研究表明反应加速度法对复杂断面的适应性更强。宾佳等[17]基于子结构法对反应位移法的原理进行了理论推导,提出了地基弹簧系数的多种求解方法并对地震荷载求解方法进行改进,通过算例对改进的反应位移法与规范中的反应位移法和整体动力时程分析方法进行对比分析,验证了改进反应位移法的实用性。禹海涛等[18]通过动力调整影响系数来考虑结构对土体的作用,进而修正自由场有效反应加速度,提高反应加速度法计算精度,并通过算例给出调整系数的取值。
由于反应位移法和反应加速度法均未直接利用反应谱进行计算,Zhao等[19-20]基于与反应加速度法相同的计算模型,给出地下设计反应谱计算方法,采用与地面建筑结构相同的反应谱分析技术,建立了考虑土-结构相互作用的地下结构抗震分析反应谱方法。本文对比反应谱法与反应位移法和反应加速度法的计算精度。
1 方法简介
1.1 反应谱法
地下结构抗震分析的反应谱法采用整体分析模型[19],如图1所示,将土-结构系统作为一个整体进行计算,模型的底面基岩固定、顶面自由、侧面采用滚轴边界,图中ug为基岩处位移。滚轴边界通过约束边界处的结点运动实现,对于水平地震作用,约束边界结点的竖向位移。滚轴边界能有效地模拟自由场反应。土-结系统采用统一模态阻尼比,确定方法如下:首先通过等效线性化场地分析软件EERA获得土体衰减模量和场地地表的位移峰值。在ABAQUS软件中建立二维自由场土柱,输入衰减的模量和模态阻尼比,两侧约束竖向运动,底边固定。输入地震动,调整土体模态阻尼比,令土柱顶部位移峰值与通过EERA获得的位移峰值相等,将该阻尼比作为土-结构系统的模态阻尼比。
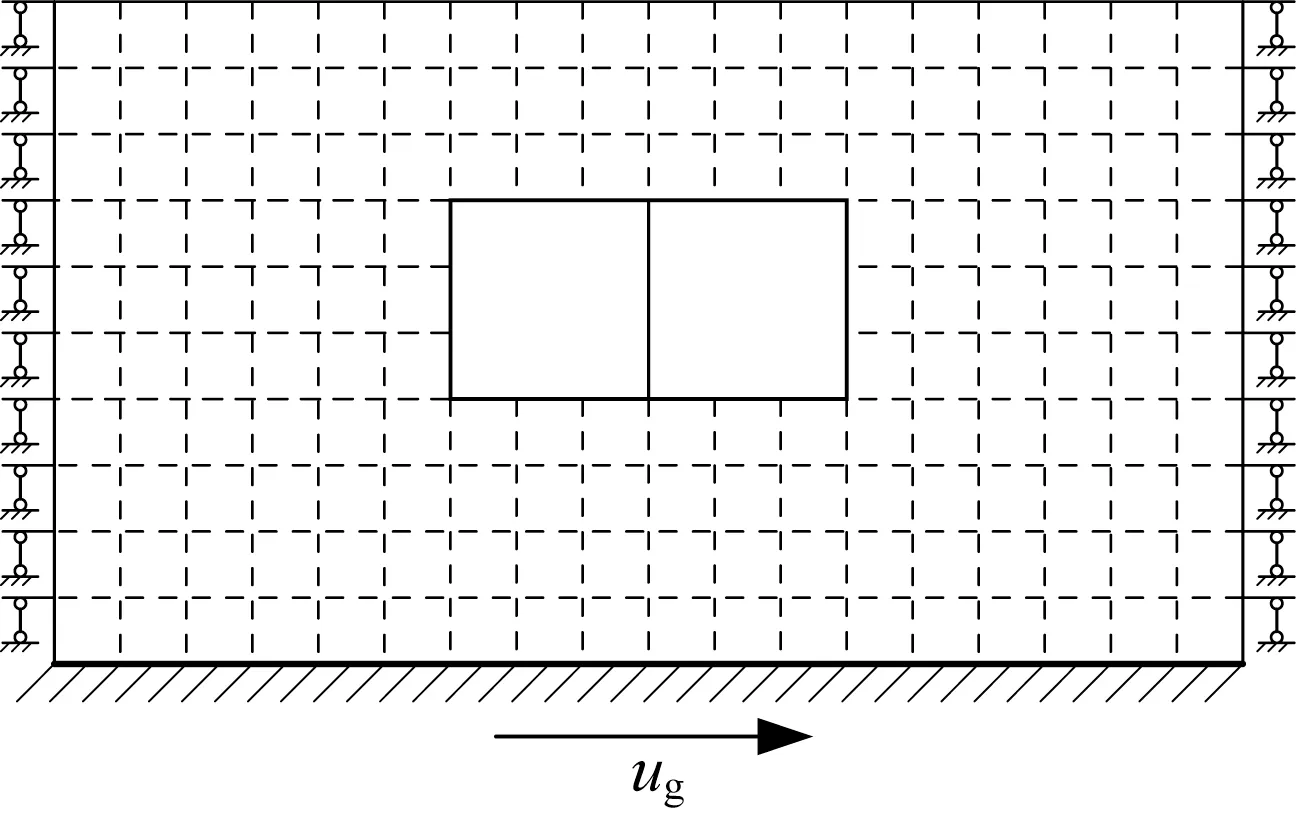
图1 反应谱法模型示意Fig.1 Schematic diagram of response spectrum method model
1.2 反应加速度法
反应加速度法的计算模型如图2所示,模型的底面基岩固定、顶面自由、侧面采用滚轴边界,在整个模型上施加惯性力。本文惯性力的确定方法如下:通过建立土柱有限元模型,提取结构顶底板相对位移最大时刻各土层的剪应力,由规范公式计算有效加速度,然后以体力的形式加在整个模型上。
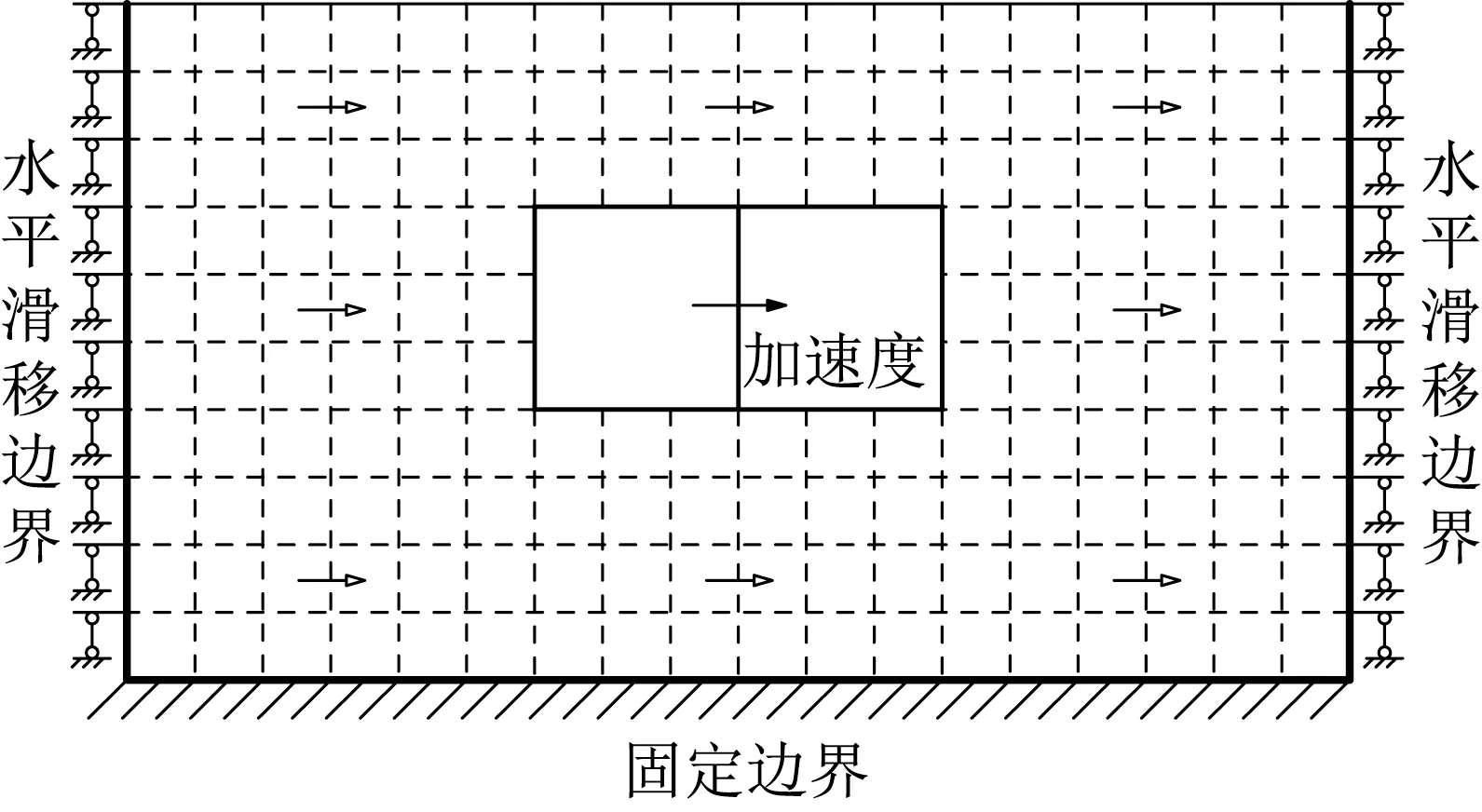
图2 反应加速度法模型示意Fig.2 Schematic diagram of response acceleration method model
1.3 反应位移法
反应位移法的模型见图3,在结构上施加的力包括三部分,分别是土层位移、土层剪力以及惯性力,各参数的确定方法如下。
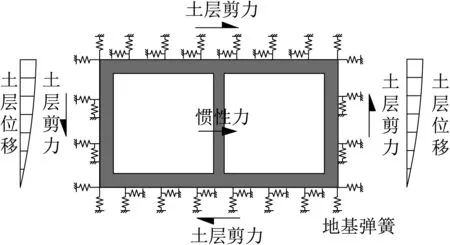
图3 反应位移法模型示意Fig.3 Schematic diagram of response displacement method model
(1)求解地基弹簧:通过静力有限元的方法,采用6次加载的方式,分别在结构顶部、底部、两侧施加水平和竖向2个方向的单位荷载,利用荷载与变形的关系求得弹簧刚度系数[21]。
(2)土层剪力:在建立的土柱模型中提取顶底板剪应力,两侧剪应力由规范公式计算得到,需要将剪应力乘以单元的长度得到剪力。要分别考虑顶板、底板、侧面施加不同方向的力。
(3)惯性力:与反应加速度法一样,施加在结构上。
反应谱法的误差来自模态组合。反应加速度法误差来自两方面,一是取最不利时刻的峰值响应确定自由场加速度,二是采用这一时刻自由场的加速度代替土-结构系统的加速度。反应位移法的误差来自地基弹簧的取值,并且地基弹簧刚度系数取值的不同对地下结构内力的计算有比较大的影响,然而目前虽有地基弹簧刚度系数取值的相关方法,但是却很难准确确定该系数。
2 数值算例
2.1 地下结构
深圳市某线路工程线路全长约9.28 km,其中地下段长度为7.49 km。结构1、结构2及结构3为该线路的车站,地面标高在36.90~45.00 m。车站几何尺寸如图4所示,结构墙体混凝土材料的密度为2 350 kg·m-3、弹性模量为31.5 GPa、泊松比为0.2,柱子混凝土材料的密度为2 500 kg·m-3,弹性模量为38.33 GPa、泊松比为0.2,二维分析时中柱弹性模量折减为10.95 GPa;结构埋深(结构顶面至地表的距离)分别为3.5 m、3.0 m和3.0 m,不考虑土体与结构间的接触非线性。
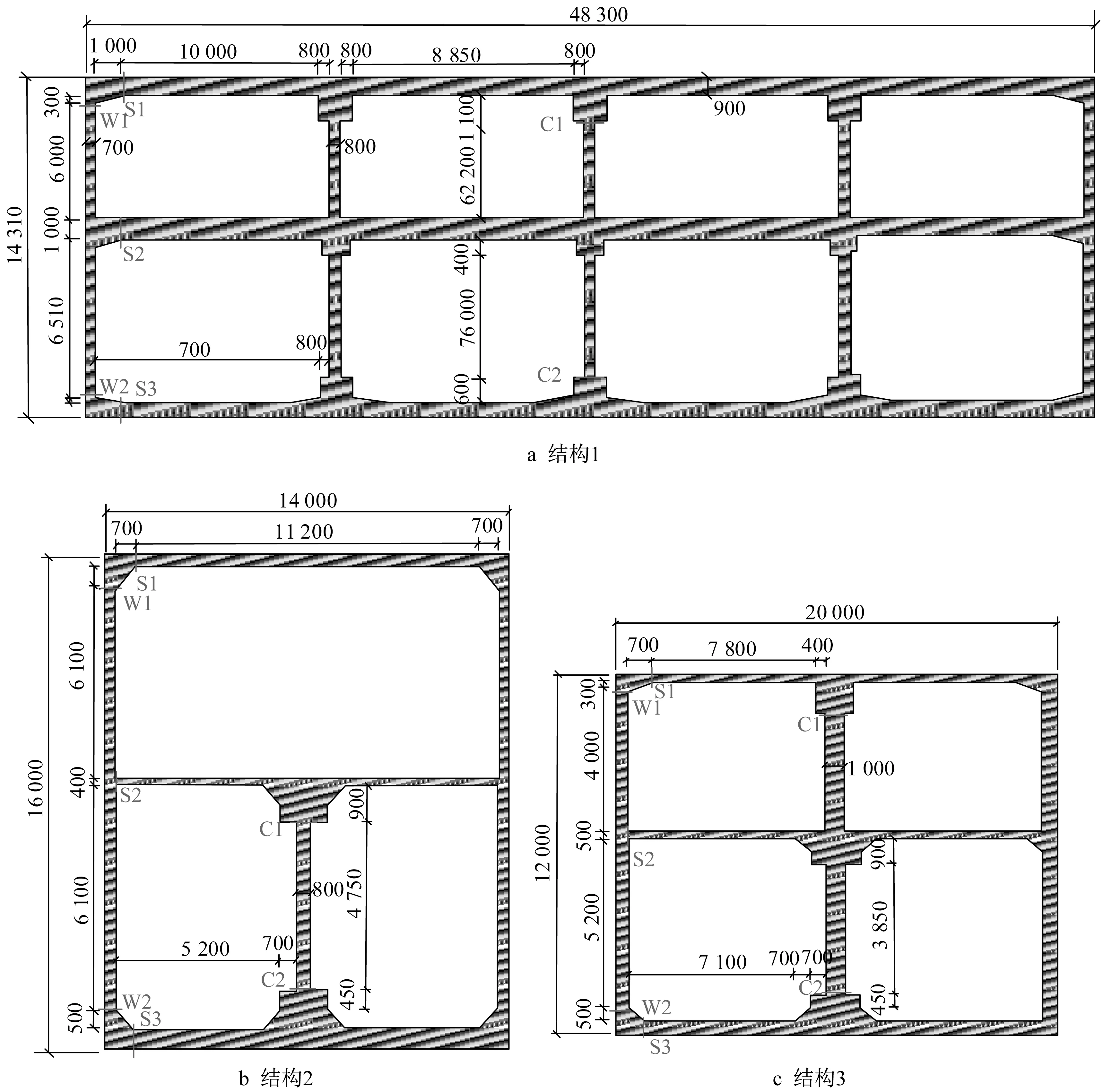
图4 地铁车站横断面(单位:mm)Fig.4 Cross-section of subway station(unit:mm)
2.2 场地
结构1所处场地由素填土、粉质黏土、微风化花岗岩组成,基岩主要是微风化大理岩;结构2所处场地由素填土、砂质黏土、全风化花岗岩、微风化花岗岩组成,基岩主要是强风化大理岩;结构3所处场地由素填土、粉质黏性土中粗砂组成,基岩主要是强风化花岗岩。
结构1场地覆盖层较浅,覆盖层向下为大理岩,场地条件可划归于较为坚硬地铁场地;而结构3位于软土地层中,土质较为软弱,场地条件可代表软弱土层场地;结构2场地的坚硬程度处在结构1与结构3之间。3个场地的参数见表1。
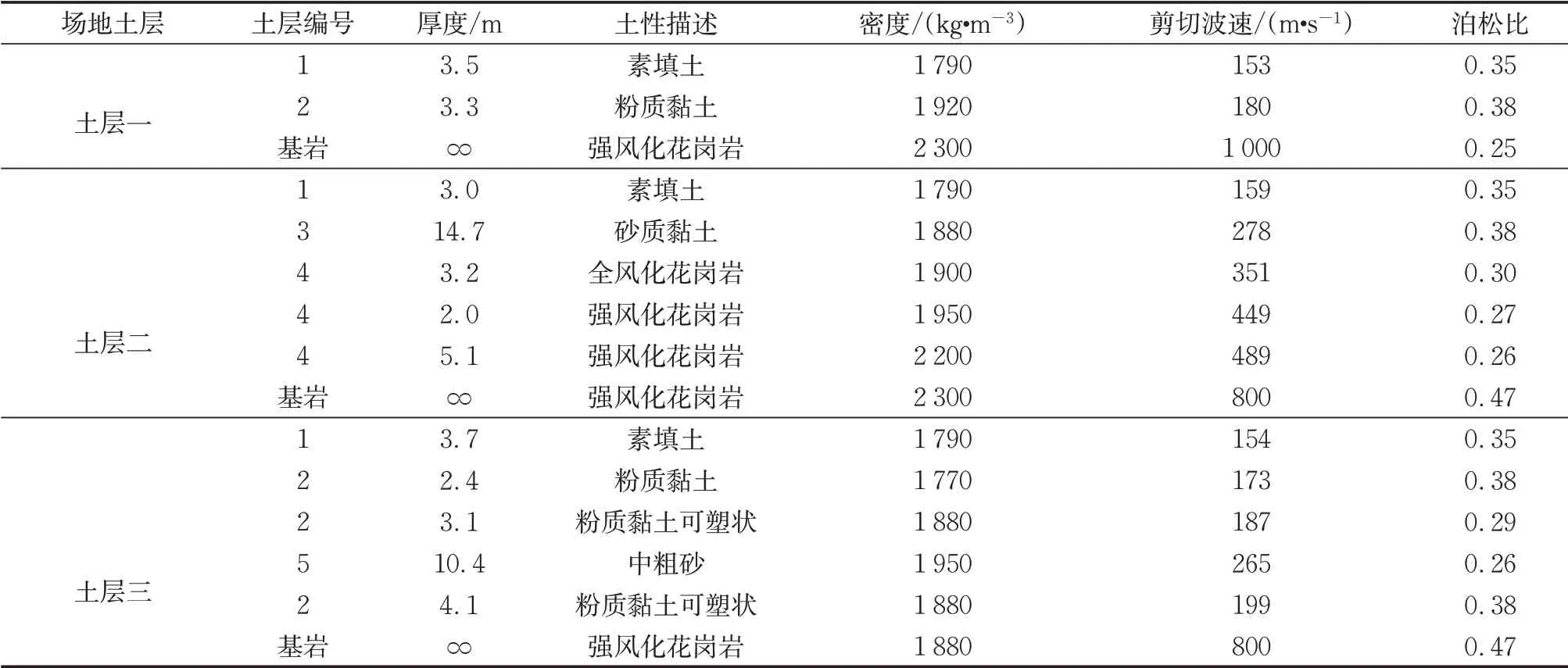
表1 土层参数Tab.1 Soil parameters
采用等效线性化模型考虑土体非线性,土体剪切模量比和阻尼比随剪应变的变化曲线如图5所示。建立基于衰减剪切模量和模态阻尼比的场地模型,模态阻尼比的确定方式见1.1节,3个场地的模态阻尼比分别为0.045、0.062和0.053。因此,土-结构模型中土体采用通过EERA程序得到的衰减模量,整个系统施加通过场地分析获得的模态阻尼比。
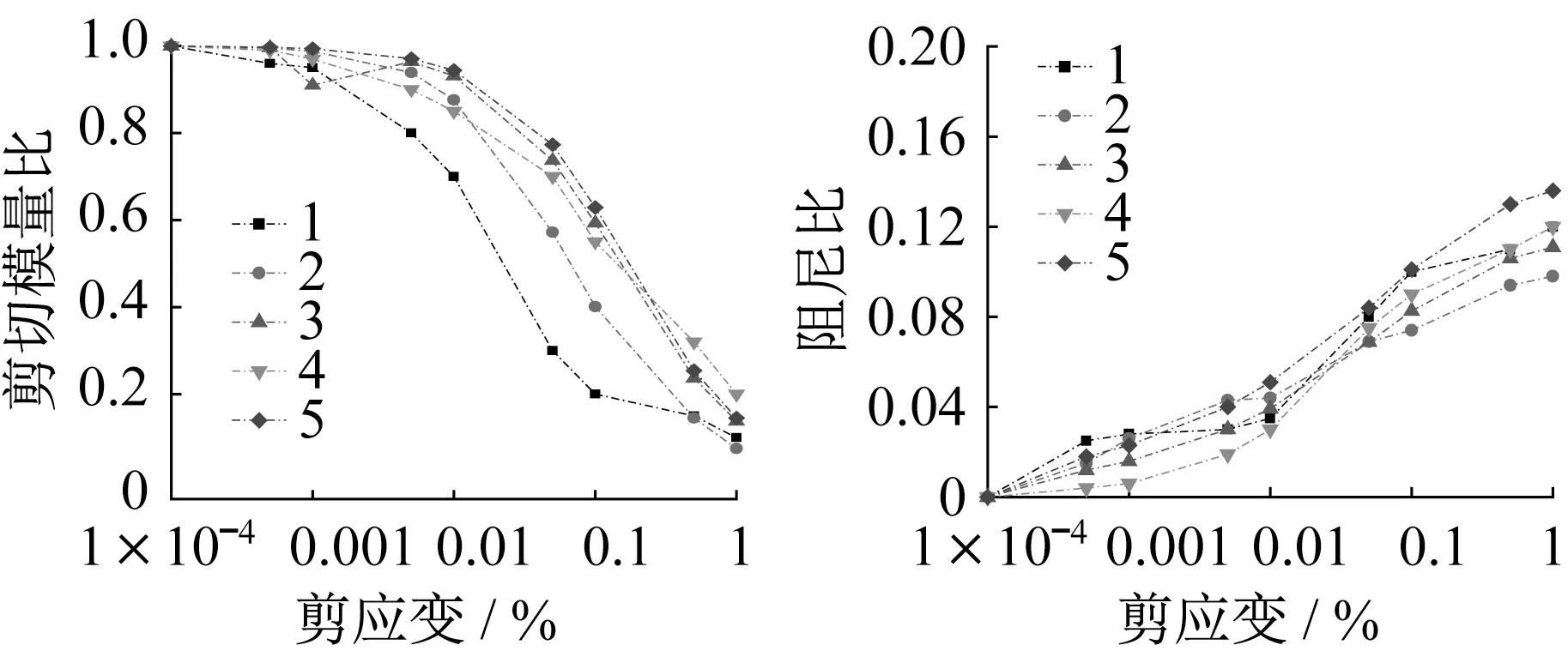
图5 剪切模量比、阻尼比随剪应变的变化曲线Fig.5 Shear modulus ratio and damping ratio versus shear strain
2.3 模型边界及地震动输入
模型中采用滚轴边界模拟被截去无限土体的土-结构相互作用效应。输入的地震记录采用地震安全性评价报告中提供的人工记录,选取E2地震作用下地震动(50年超越概率10%),结构1基岩地震动峰值加速度为0.07g,结构2基岩地震动峰值加速度为0.08g,结构3基岩地震动峰值加速度为0.10g。地震动加速度时程曲线见图6。
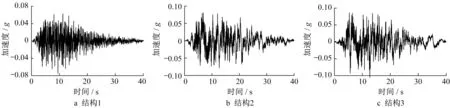
图6 地震动加速度时程曲线Fig.6 Acceleration time history curve of ground motion
2.4 二维土-结构相互作用模型及参数
有限元模型如图7所示,土体采用实体单元,车站结构采用梁单元,土体按照数值模拟精度要求离散,单元网格尺寸满足1/8~1/6的地震波波长要求,结构所在位置相邻土体进行网格细化。结构1整体模型节点数共8 649个,单元数共8 458个;结构2整体模型节点数共8 649个,单元数共8 376个;结构3整体模型节点数共7 793个,单元数共7 520个。土体与主体结构之间绑定。按照《城市轨道交通结构抗震设计规范:GB 50909—2014》[7]6.7节要求,模型底面可取设计地震作用基准面,顶面取地表面,侧面边界到结构的距离宜取结构水平有效宽度的2~3倍,故模型的场地尺寸满足规范要求。

图7 二维有限元模型(单位:m)Fig.7 Two-dimensional finite element model(unit:m)
3 结果讨论
3.1 结构变形分析
在基岩地震动作用下,得到车站顶层层间位移及底层层间位移柱状图如图8所示。为分析各种简化方法之间的精度,以动力时程法计算结果为参考解,得到反应谱法、反应加速度法和反应位移法的误差,结果表明,反应谱法的误差范围为2%~14%,反应加速度法的误差为2%~26%,反应位移法的误差为9%~44%,反应谱法得到的层间位移值更接近动力时程法。
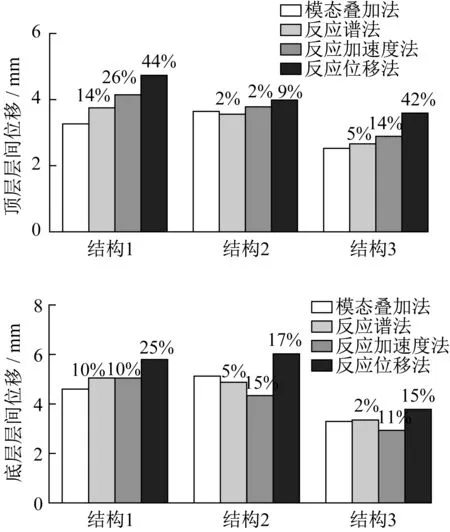
图8 结构变形图Fig.8 Diagram of structural deformation
3.2 结构内力分析
选取中柱顶部及底部、侧墙顶部及底部、顶板与中板和底板作为关键截面分析,截面位置如图4所示。
3.2.1 弯矩分析
结构弯矩柱状图如图9所示。从图中可以看出,对于结构1来说,反应谱法的误差为5%~10%,反应加速度法的误差为7%~14%,反应位移法的误差为13%~35%;对于结构2来说,反应谱法的误差为1%~12%,反应加速度法的误差为6%~17%,反应位移法的误差为10%~32%;对于结构3来说,反应谱法的误差为2%~14%,反应加速度法的误差为5%~18%,反应位移法的误差为10%~42%。因此,反应谱法得到各截面位置处的弯矩值更接近动力时程法。
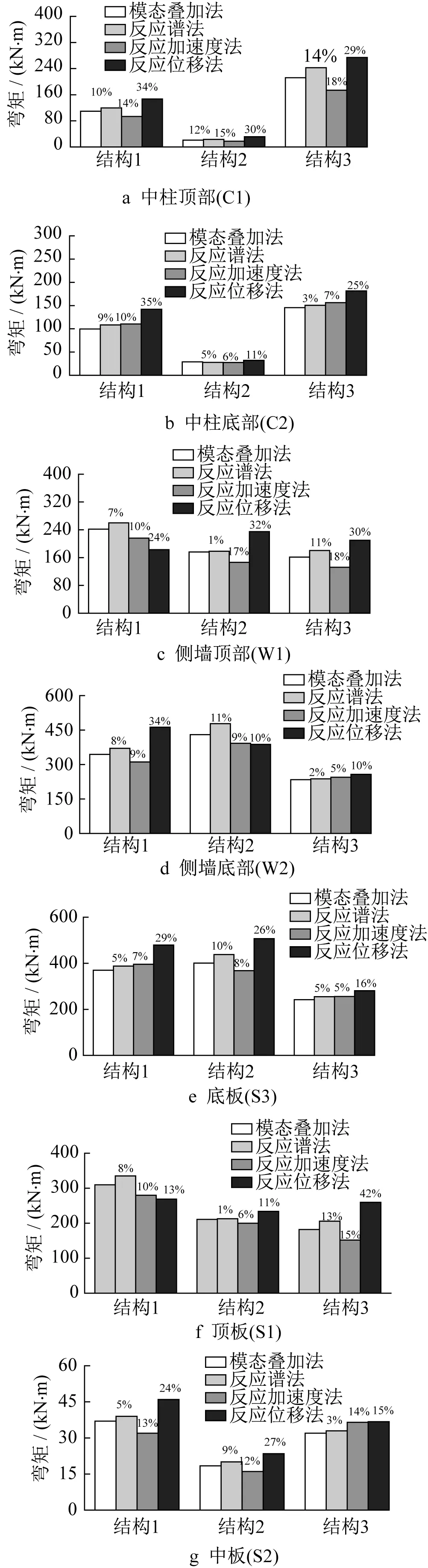
图9 结构弯矩图Fig.9 Diagram of structural bending moment
3.2.2 剪力分析
结构剪力柱状图如图10所示。从图中分析得出,对于结构1来说,反应谱法的误差为0.5%~10%,反应加速度法的误差为0.2%~18%,反应位移法的误差为14%~35%;对于结构2来说,反应谱法的误差为0.1%~10%,反应加速度法的误差为1%~20%,反应位移法的误差为16%~32%;对于结构3来说,反应谱法的误差为3%~11%,反应加速度法的误差为1%~12%,反应位移法的误差为17%~31%。因此,反应谱法得到各截面位置处的剪力值更接近动力时程法。
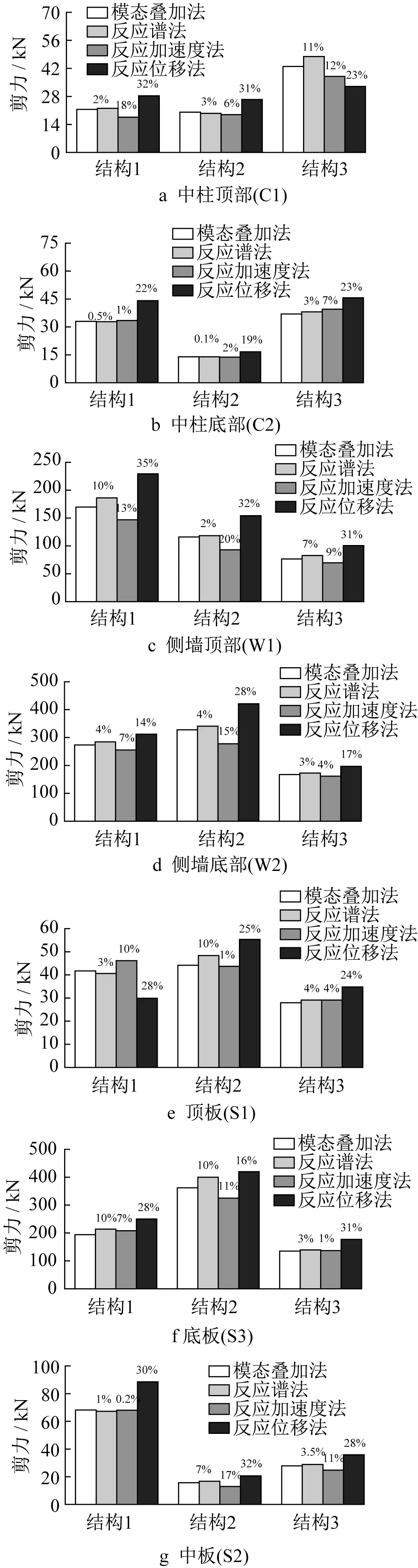
图10 结构剪力图Fig.10 Diagram of structural shear force
4 结论
以深圳市某线路工程地铁站抗震分析为例,比较反应谱法、反应加速度法和反应位移法的计算精度。初步研究表明,反应谱方法计算的结构层间位移在2%~14%,截面内力误差为0.1%~14%;反应加速度法计算的结构层间位移为2%~26%,截面内力误差为0.2%~20%之间;反应位移法计算的结构层间位移为9%~44%,截面内力为10%~42%;反应谱法精度较高,可以作为地下结构抗震设计分析方法。
作者贡献说明:
赵密:提出创新点,修改论文。
李苗:计算、撰写初稿。
昝子卉:提供数据。
高志懂:修改论文。
杜修力:修改论文、基金支持。
王君杰:修改论文。

