砂土中垫层隔震基础地震响应离心模型试验及数值分析
张 浩,贾亚杰,梁发云,李通达
(1.同济大学土木工程学院,上海200092;2.上海师范大学建筑工程学院,上海201418)
近年来国内外学者不断探讨适用于地震带深水环境的基础型式,其中Rion-Antirion桥[1]具有较好的代表性。该桥持力层为深厚的软弱冲积层,采用钢管桩加固软弱土体,在其上覆砂石垫层,并将预制装配式主塔基础明置于砂石垫层之上,从而形成垫层隔震基础。这种垫层隔震基础的关键创新之处在于:一方面,砂石垫层可以消减传递至上部结构的地震作用,保护桥梁上部结构;另一方面,桩顶与主塔基础并不直接连接,桩顶约束减弱,上部结构施加给桩身的惯性作用降低;此外,主塔基础以预制装配式为主,桩顶与主塔基础无需刚性连接,在深水环境中的施工难度大幅度降低。Rion-Antirion桥在2004年建成后经历了数次6级以上地震的考验[2],对我国强震地区深水桥梁的建设具有重要的参考价值。
垫层隔震基础虽然在Rion-Antirion桥等实际工程中得到了成功应用,但更多地是从概念上把握,将加固后的土体作为均质地基,采用明置基础的设计方法[1],其中仍有一些关键问题亟待解决,如垫层对于刚性基桩及上部结构地震动力响应的影响机制等。此外,垫层隔震基础虽然目前在桥梁工程领域运用较少,但与此基础形式类似的复合地基基础(非连接式桩筏基础)在建筑工程领域已经有着较为广泛的运用;然而,目前针对此类基础的研究也主要集中在静力方面[3-5],对其动力性能方面的研究却相对较少[6]。武思宇等[7-8]以建筑基础为背景,初步研究了垫层隔震基础的地震响应。韩小雷等[9]和Han等[10]采用数值模拟研究了地震作用下复合地基-筏板-建筑结构的动力响应,分析了该基础的隔震效果。Gorini和Callisto[11]亦采用数值分析研究了与垫层隔震基础相似的摩擦耗能基础的地震响应。文献[12]则通过对比浅基础、桩筏基础和垫层隔震基础的离心模型试验结果,指出与浅基础和桩筏基础相比,垫层隔震基础可以显著降低基础沉降和上部结构传递至基础的惯性力。已有文献多以建筑基础为背景,通过数值模拟或离心振动台试验分析垫层隔震基础的地震响应,但对垫层隔震机理方面的研究仍然较少。鉴于此,Liang等[13]参考Rion-Antirion桥基础形式,忽略主塔基础形状并假设与垫层接触的上覆刚性基础为筏板,开展了软黏土中垫层隔震基础-桥梁上部结构体系的离心振动台试验,重点研究了不同地震波作用下垫层对隔震基础-上部结构体系动力响应的影响机制。
国内外多个拟建的跨海工程位于地质条件复杂的深水环境中,其海底以下相当范围内为砂土地基[14-15]。本文在上述研究的基础上,针对砂土场地中的群桩基础(连接式桩筏基础)和垫层隔震基础(非连接式桩筏基础)开展地基-基础-结构动力相互作用的离心振动台试验,并额外加入大振幅的长周期地震波输入,对比不同峰值长短周期地震波作用下群桩基础和垫层隔震基础的动力响应,分析上部结构惯性效应和土体运动作用对2种基础地震反应的影响,着重探讨垫层隔震基础的隔震机理。此外,结合动力离心模型试验,采用Abaqus软件建立三维有限元模型,开展参数分析,进一步研究垫层刚度和垫层厚度对垫层隔震基础地震动力响应的影响规律。
1 垫层隔震机理的离心模型试验
试验采用同济大学的TLJ-150型岩土离心机。开展试验时,最大离心加速度50g,最大振动加速度20g,最大振幅6 mm,激振最长持时1 s,振动频率20~200 Hz。离心机配置了由22层框架叠合而成的层状剪切箱,每层框架厚24 mm。为吸收反射波,剪切箱内壁贴有1 mm厚橡胶膜。
1.1 试验模型
试验土体采用普通干砂,级配曲线如图1所示,绝大部分粒径位于0.05~0.20 mm之间。砂土密度1 450 kg·m-3,试验填土在50g应力条件下平均剪切波速约100 m·s-1。
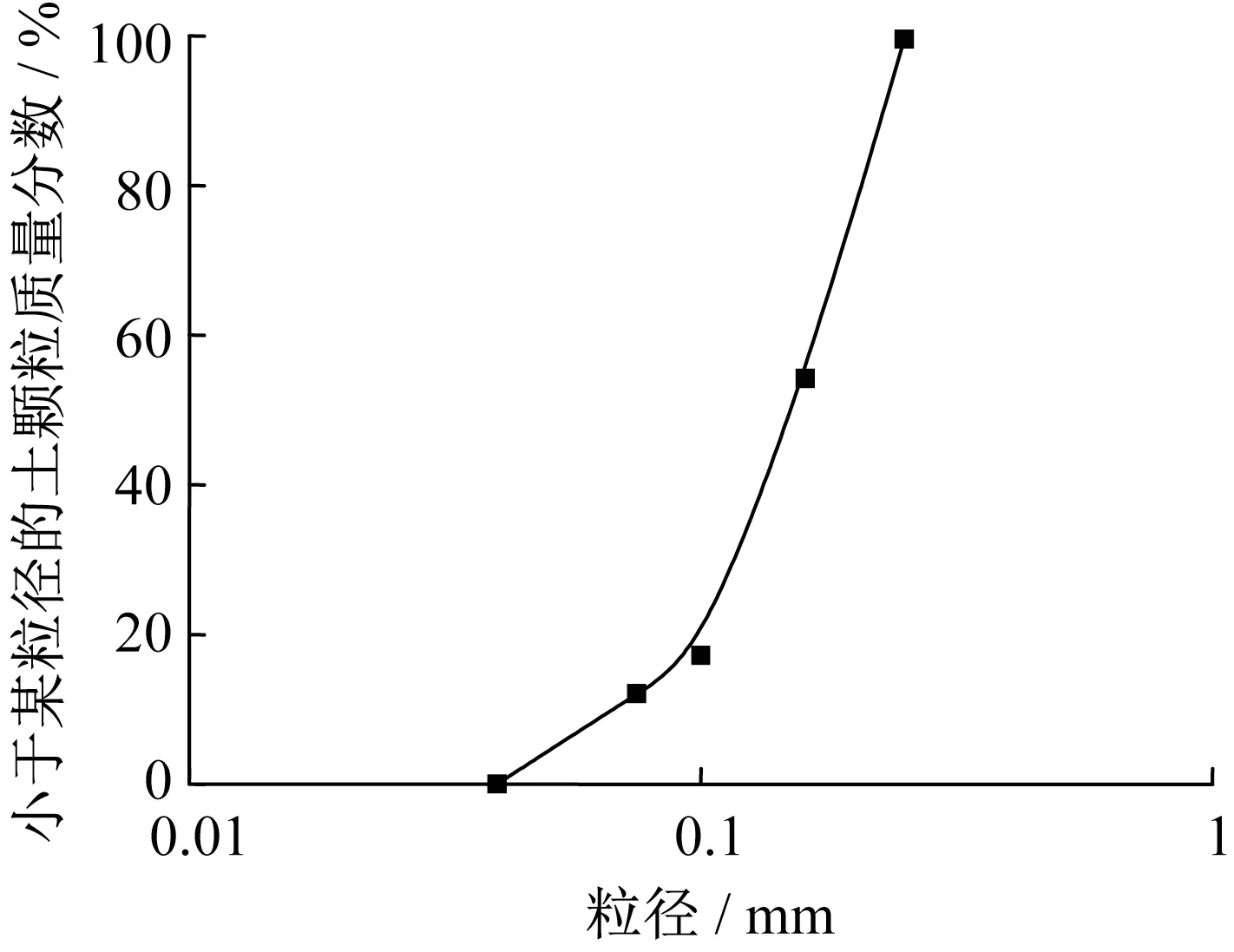
图1 砂土级配曲线Fig.1 Distribution curve of particle size of sand
设计离心加速度50g,模型与原型长度相似比为1:50,模型几何、材料及动力特性相似比如表1所示。立柱、承台(筏板)及桩采用铝合金材料,上部集中质量采用钢铁,模型尺寸及材料参数如表2所示。图2为试验模型。

图2 试验模型Fig.2 Test model
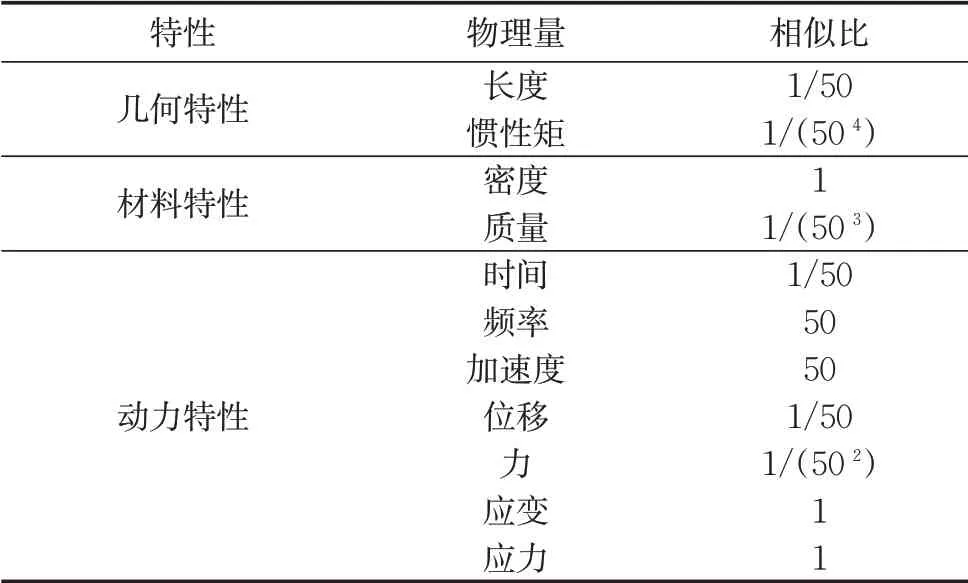
表1 模型试验相似比Tab.1 Similitude relationships

表2 模型尺寸及参数Tab.2 Dimensions and parameters of model
1.2 传感器布置
采用加速度传感器、差动式位移传感器、激光位移传感器和应变片分别测量模型的加速度、位移以及桩身和立柱的弯曲变形(弯矩)。各传感器编号及功能如表3所示,传感器位置如图3所示。值得注意的是,群桩基础(连接式桩筏基础)和垫层隔震基础(非连接式桩筏基础)模型采用同一套上部结构、立柱及桩基础,且垫层厚度为1倍桩径(对应原型0.6 m);只是在开展模型试验时,群桩基础桩顶与承台采用夹紧连接,夹紧长度为承台厚度(20 mm),而垫层隔震基础模型筏板为完整方形铝合金板,与桩顶不连接;故垫层隔震基础模型桩长270 mm(对应原型13.5 m),群桩基础桩长250 mm(对应原型12.5 m)。
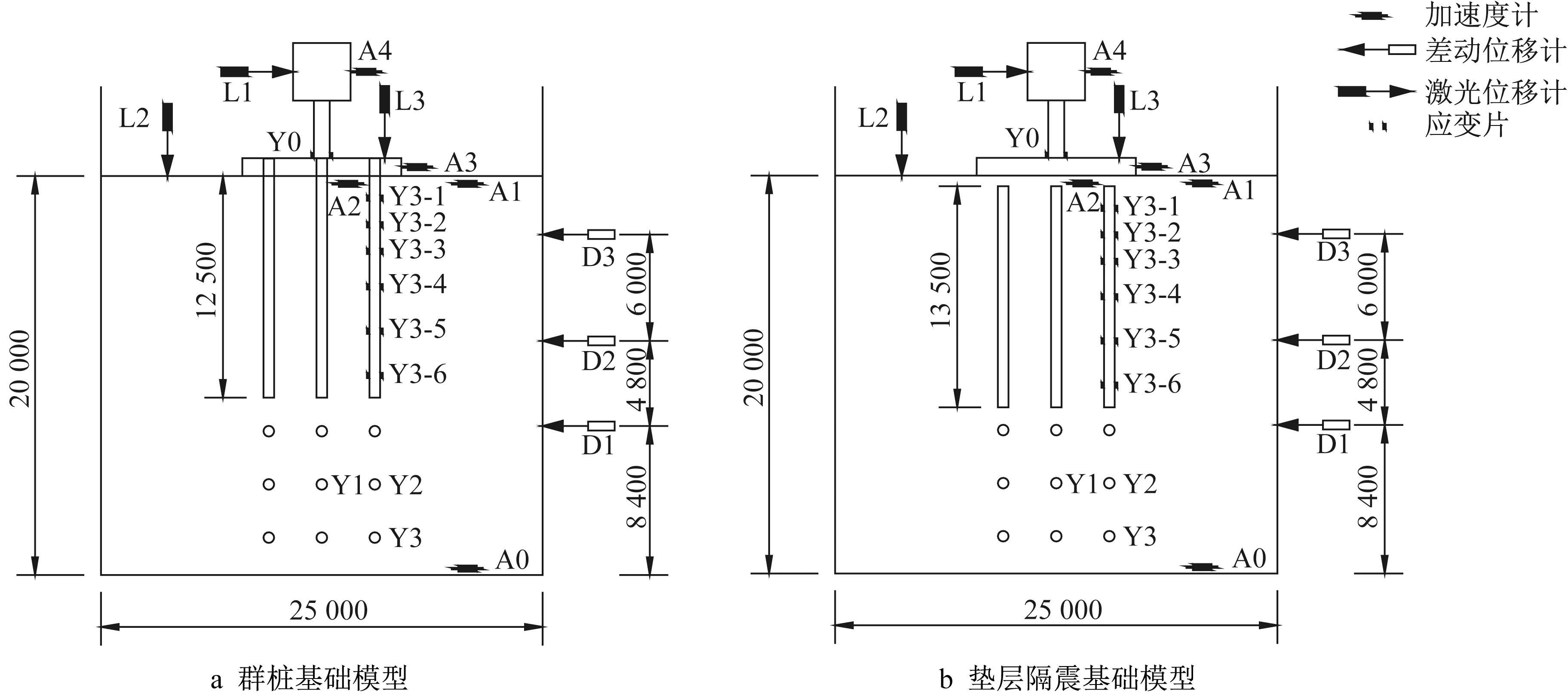
图3 试验模型及传感器布置(单位:mm)Fig.3 Schematic view of model and instruments in centrifuge tests(unit:mm)
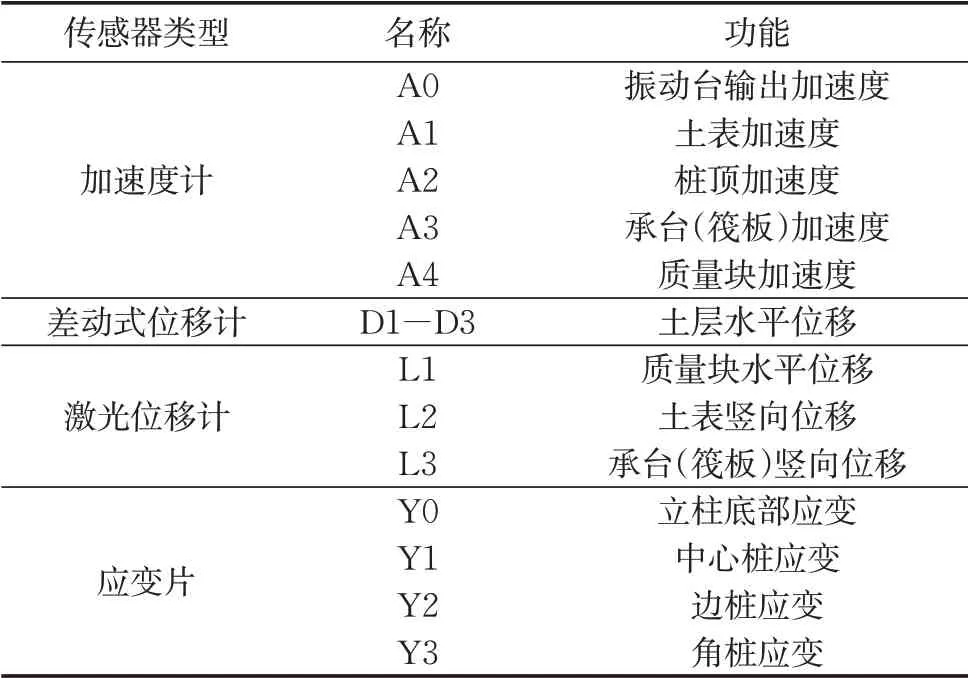
表3 各传感器功能Tab.3 Function of each sensor
1.3 加载方案
地震波采用短周期成分丰富的El Centro波和长周期成分丰富的Mexico City波,并通过振动台从模型箱外部施加水平地震波。因振动台激振频率为20~200 Hz,激振前,先根据相似比调整激振时间和振动幅值,然后对调整后的地震波进行20~200 Hz带通滤波处理。图4为处理后的地震波时程、傅里叶谱及反应谱,需要指出的是,为便于分析,图4为激振试验所对应的原型尺寸地震波。本试验依次增加地震波峰值,激振El Centro波和Mexico City波,激振顺序及工况名称如表4所示。
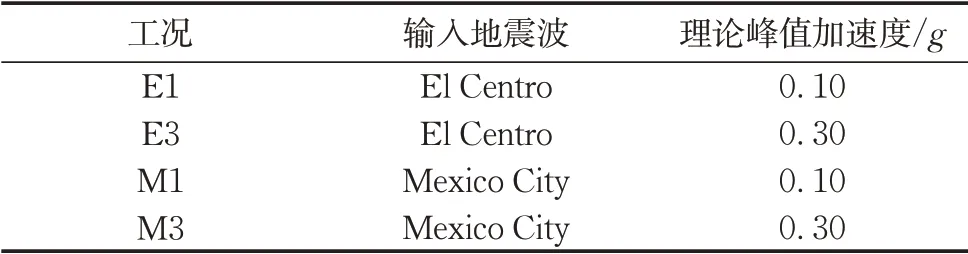
表4 加载方案Tab.4 Test cases
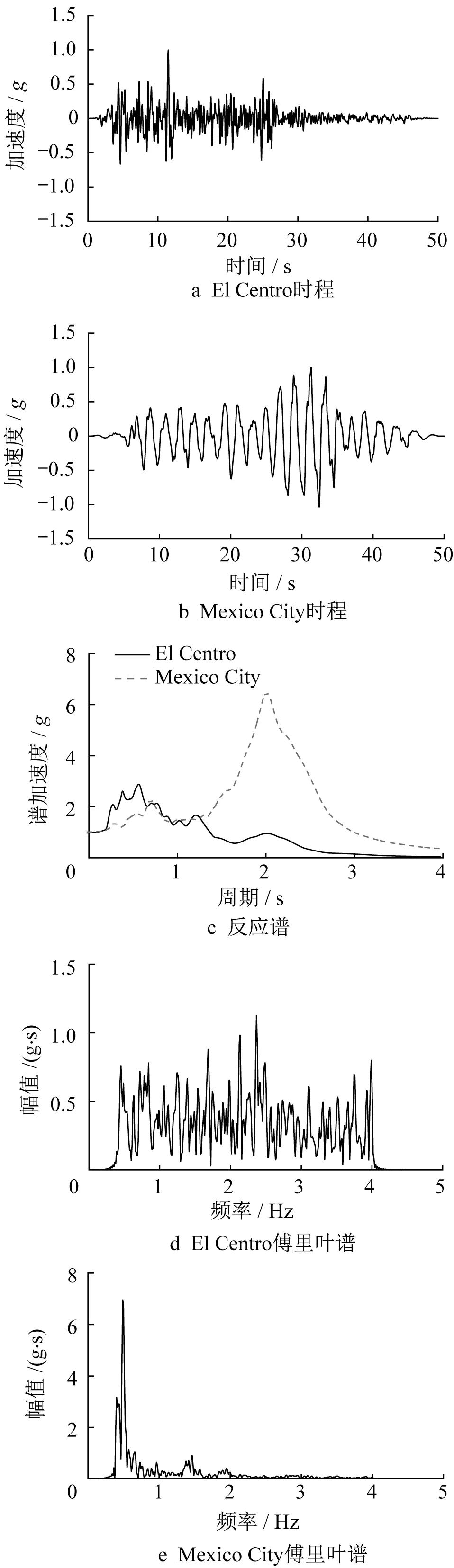
图4 输入地震波时程、傅里叶谱及反应谱Fig.4 Time history,Fourier spectrum,and response spectrum of input seismic wave
1.4 试验结果及分析
为便于分析,所有试验结果均等效为原型结果。为验证系统的可靠性,在土体底部布置加速度传感器,并对比土底加速度和振动台反馈加速度,比较二者是否一致。设振动台反馈加速度傅里叶谱为F0(f),土底加速度傅里叶谱为G0(f),则土底加速度与反馈加速度传递函数为Z0(f)=G0(f)/F0(f),其幅值|Z0(f)|为加速度放大谱。图5为白噪声激振下的土底-振动台加速度传递函数,该放大谱幅值在0.4~4 Hz范围内保持在1附近,表明土底加速度和振动台反馈加速度基本一致,剪切箱与振动台之间加速度传递效果可靠,振动台输出加速度可视为土底实际输入加速度。此外,为保持群桩基础(连接式桩筏基础)模型和垫层隔震基础(非连接式桩筏基础)模型结果的可对比性,有必要保持2组模型试验的振动台输入地震波一致,且地表加速度相近。图6为群桩基础模型和垫层隔震基础模型4组试验的振动台输出加速度反应谱,虽然二者与理论输出加速度反应谱(图4)之间存在一定的差别,但4种工况下上述2类基础模型试验得到的振动台输出加速度反应谱非常接近,说明振动台对同一种地震波的重复性较好。图7为2组试验4种工况下的地表加速度反应谱,不同工况下的地表加速度反应谱均较为接近,进一步说明了2组试验模型土的物理力学性质相似,且试验结果的可对比性较高。
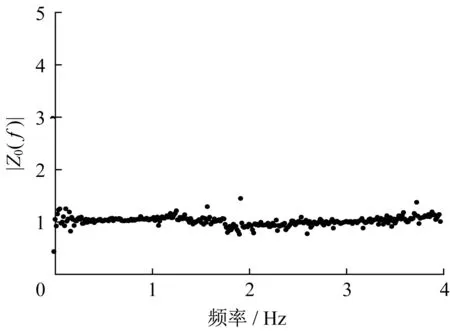
图5 土底-振动台加速度传递函数Fig.5 Acceleration transfer function of soil bottomshaking table
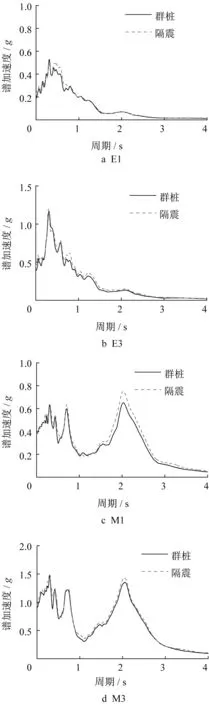
图6 振动台输出加速度反应谱Fig.6 Acceleration response spectrum of output motion
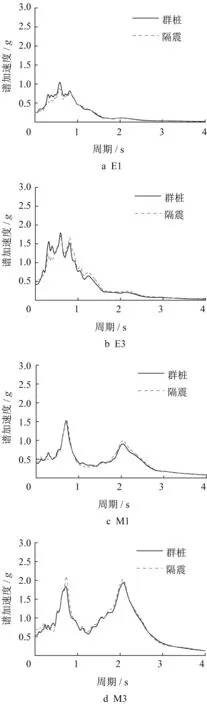
图7 地表加速度反应谱Fig.7 Acceleration response spectrum of ground surface
1.4.1 上部结构-筏板加速度
图8为群桩基础模型和垫层隔震基础模型的上部结构加速度。当输入地震波加速度峰值较小时,2种模型的上部结构加速度时程及傅里叶谱相似。输入地震波加速度峰值增加,二者差异增加,垫层隔震基础模型上部结构加速度时程峰值及其傅里叶谱幅值均小于同种工况下的群桩基础,且频率分布上也产生了一定变化,表明垫层起到了隔震作用。具体而言,输入地震波为0.1g和0.3g的El Centro波时,垫层隔震基础模型上部结构加速度正(负)峰值与群桩基础上部结构加速度正(负)峰值的比例分别为1.00(1.00)和0.65(0.81);输入地震波为0.1g和0.3g的Mexico City波时,二者比例分别为0.68(0.74)和0.59(0.73),即强震时垫层隔震基础模型上部结构加速度峰值约为群桩基础上部结构加速度峰值的60%~80%,垫层隔震作用显著。
导致垫层隔震基础模型与群桩基础模型的上部结构加速度不同的原因可能有2种:①群桩基础的承台与垫层隔震基础的筏板加速度不同,导致输入上部结构(立柱-上部质量块)的加速度不同;②因承台与筏板的底部约束不同,承台-结构与筏板-结构体系的动力特性不同,从而导致上部结构加速度响应不同。
图9为各工况群桩基础模型承台和垫层隔震基础模型筏板加速度反应谱。输入地震波为0.1g的El Centro波时,承台与筏板的加速度反应谱相似,输入地震波为0.3g的El Centro波时,垫层隔震基础的筏板谱加速度峰值明显小于群桩基础的承台谱加速度峰值。输入地震波为Mexico City波时,垫层隔震基础的筏板谱加速度在0~0.5 s范围内大于群桩基础承台的谱加速度;而在0.5~1.0 s范围内,则小于群桩基础承台的谱加速度。

图9 筏板(承台)加速度反应谱Fig.9 Acceleration response spectrum of raft(cap)
设筏板(承台)的加速度傅里叶谱为F(f),上部结构的加速度傅里叶谱为G(f),则上部结构/筏板(承台)的加速度传递函数为Z(f)=G(f)/F(f),传递函数的幅值|Z(f)|为加速度放大谱。图10 a、10 b和图10 c、10 d分别为群桩基础(连接式桩筏基础)的上部结构-承台和垫层隔震基础(非连接式桩筏基础)的上部结构-筏板传递函数。群桩基础的上部结构-承台加速度传递函数几乎不随输入地震波的变化而改变,各工况传递函数峰值对应的频率均为1.5 Hz左右,即上部结构自振周期约为0.67 s。垫层隔震基础的上部结构-筏板加速度传递函数则随着输入地震波的改变而发生显著变化;输入地震波分 别 为0.1g的El Centro和0.3g的Mexico City波时,传递函数峰值对应的频率分别约为1.6 Hz和1.2 Hz,即自振周期分别约为0.63 s和0.83 s,上部结构体系自振周期逐渐增加。这是由于随着输入地震波加速度峰值的增加,群桩基础模型的基础对上部结构的约束强度几乎不变,而隔震基础模型的基础对上部结构的约束逐渐减弱;即遭遇强震时,垫层与筏板之间将产生相对滑移,进而改变结构体系的刚度,其自振周期也会相应发生变化。
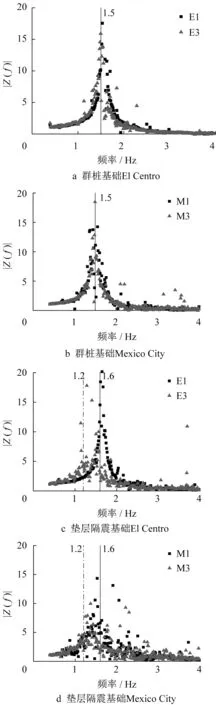
图10 上部结构-筏板(承台)加速度传递函数Fig.10 Acceleration transfer function of superstructure-raft(cap)
1.4.2 上部结构位移
图11为各工况群桩基础模型(连接式桩筏基础)和垫层隔震基础模型(非连接式桩筏基础)上部结构相对振动台位移时程。
从图11可以看出,输入地震波为0.1g和0.3g的El Centro波时,群桩基础模型的上部结构残余位移分别为1.8 mm和-3.7 mm,垫层隔震基础上部结构残余位移分别为18.3 mm和45.8 mm;输入地震波为0.1g和0.3g的Mexico City波时,群桩基础模型的上部结构残余位移均为5.5 mm,垫层隔震基础上部结构残余位移分别为78.7 mm和122.7 mm。因群桩基础桩顶与承台刚性连接,故上部结构残余位移较小;而垫层隔震基础因筏板与刚性桩无直接连接,筏板水平向的约束只有筏板与垫层之间的摩擦作用,水平向约束要小得多,故上部结构残余位移较大;群桩基础上部结构残余位移远小于垫层隔震基础上部结构残余位移。
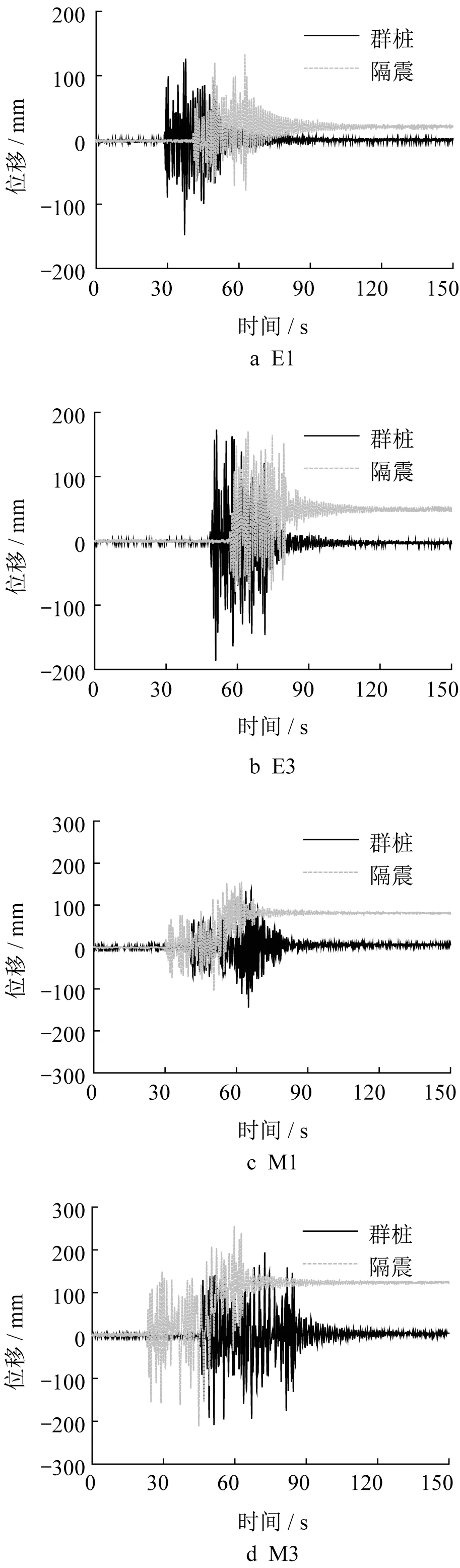
图11 上部结构位移时程Fig.11 Displacement time history of superstructure
1.4.3 立柱与基桩弯矩
表5为2组模型各工况立柱弯矩正负峰值。输入地震波为0.1g和0.3g的El Centro波时,垫层隔震基础模型立柱弯矩正(负)峰值与群桩基础模型立柱弯矩正(负)峰值的比例分别为1.00(0.90)和0.76(0.69);输入地震波为0.1g和0.3g的Mexico City波时,二者比例分别为0.61(0.62)和0.63(0.78)。强震时垫层隔震基础模型立柱弯矩约为群桩基础模型立柱弯矩的60%~80%,垫层隔震作用显著。
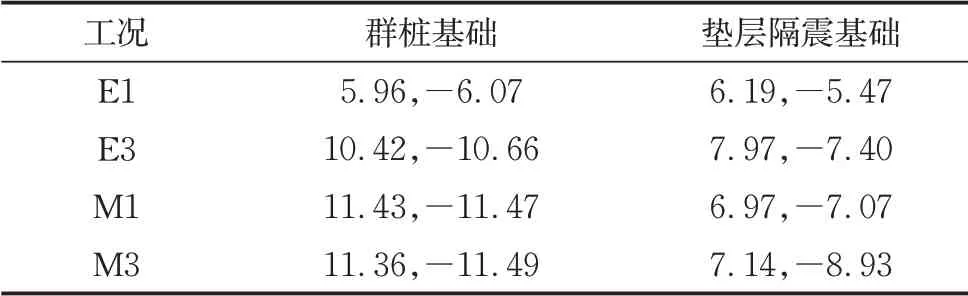
表5 立柱弯矩正(负)峰值Tab.5 Positive and negative peak bending moment of column 单位:MN·m
图12a和图12b分别为群桩基础模型和垫层隔震基础模型在M3工况下的中心桩和角桩峰值弯矩。群桩基础中心桩和角桩的顶部测点处弯矩最大,而垫层隔震基础中心桩和角桩的中部测点处弯矩最大,最大弯矩峰值约为群桩基础最大弯矩峰值的50%~60%。与群桩基础的刚性连接相比,垫层隔震基础的桩顶约束要弱得多,且强震作用下上部结构作用于隔震基础的惯性力要小于群桩基础的惯性力,故垫层隔震基础将桩与筏板断开可有效降低桩身的峰值弯矩。值得一提的是,群桩基础和垫层隔震基础模型采用同一套桩基模型;群桩基础因桩顶接触连接需要,夹入承台内部2 cm(原型为1.0 m),而垫层隔震基础筏板与桩顶之间却有着厚度为1倍桩径(原型为0.6 m)的垫层;故同一桩基应变片在2组模型中的埋深不同,其各自实际测点亦如图12标记点位置所示。
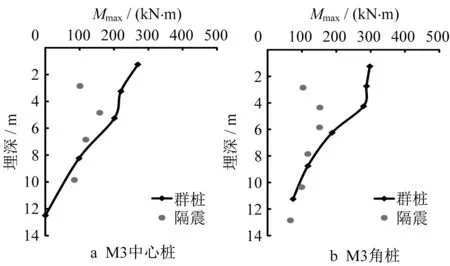
图12 基桩峰值弯矩Fig.12 Peak bending moment of pile
2 影响因素的三维数值分析
基于前文群桩基础(连接式桩筏基础)与垫层隔震基础(非连接式桩筏基础)的离心振动台试验,采用ABAQUS软件建立三维数值有限元模型。首先对比数值模拟和离心振动台试验的结果,验证三维数值模型的合理性;然后对比群桩基础模型和垫层隔震基础模型的筏板转角和桩身弯矩,进一步探讨垫层隔震基础的隔震机理;最后开展参数分析,研究垫层刚度和垫层厚度对垫层隔震基础地震响应的影响。
2.1 三维数值模型的建立
采用有限元方法分析基础地震响应时,选择合适的模型边界至关重要。为减小边界反射波对计算结果的影响,常采用的边界有黏性边界、黏弹性边界、无限元边界和等位移边界。黏性边界及黏弹性边界通过在土体外侧施加黏性元件或黏弹性元件吸收应力波[16]。无限元边界本质上与黏弹性边界相似,但无需计算元件参数[10]。等位移边界定义模型侧面相同高度处位移相同,无需计算元件参数,可以较好地模拟层状剪切箱的侧面边界[17-18]。本文采用等位移边界模拟土体侧向边界,同时适当增加振动方向土体计算区域,以降低反射波的影响。
因主要研究垫层隔震基础(非连接式桩筏基础)的隔震机理,故土体采用较为常用、参数较少且易于确定的弹性模型。根据前文离心振动台试验建立有限元模型并确定模型参数,土体密度1 450 kg·m-3,弹性模量50.0 Mpa,泊松比0.3,阻尼采用Rayleigh阻尼模型,即C=αM+βK,其中C为阻尼矩阵、M为质量矩阵、K为刚度矩阵、α和β分别为2个比例系数,阻尼比取10%,在ABAQUS软件中,设置α=0.942,β=0.010 6[19]。模型集中质量、立柱、筏板及桩的参数如表2所示,并根据离心模型试验所用材料反算出原型尺寸确定,其中上部结构材料为铁,立柱和筏板材料为铝,桩身弹性模量根据抗弯刚度等效,将空心桩等效为实心桩。
土体尺寸为40 m×30 m×20 m,采用C3D8R单元类型,全局网格尺寸1m,局部加密尺寸0.5 m,土体共包含85 760个单元。分别建立群桩基础模型(连接式桩筏基础)和垫层隔震基础模型(非连接式桩筏基础)。群桩基础模型桩顶与承台采用Tie接触,垫层隔震基础模型筏板与垫层采用接触对摩擦接触。通过设置同一高度处模型四周节点位移相同实现等位移边界,模型如图13所示。
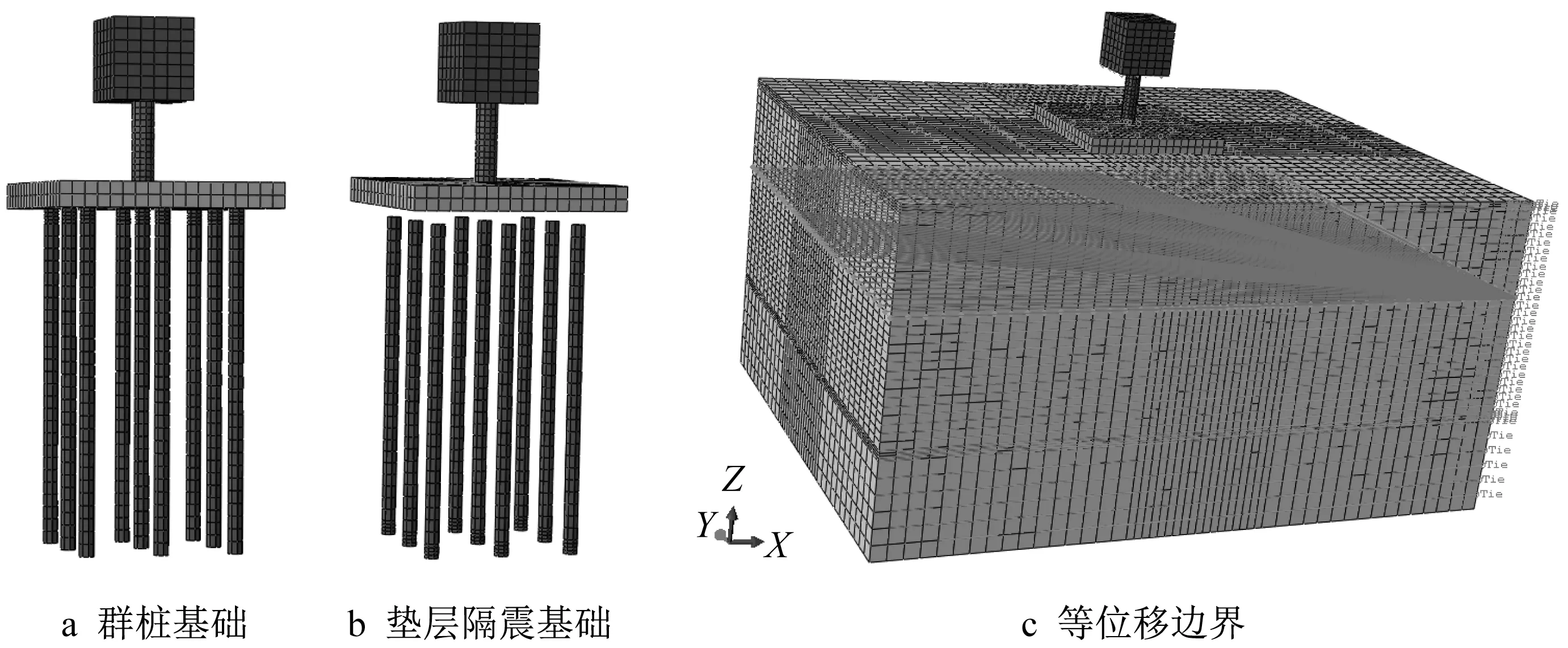
图13 三维数值计算模型Fig.13 Three dimensional numerical model
模型分析包含3个步骤:①平衡地应力;②施加上部结构荷载;③施加地震荷载。地震波采用El Centro地震波,时间间隔0.02 s,地震波时程、傅里叶谱及反应谱如图4所示。
2.2 模型验证
对比数值模拟和前文离心振动台试验结果,以验证所建立的有限元模型的合理性。图14为输入地震波为0.1g的El Centro波时,群桩基础模型振动台试验和有限元结果。值得注意的是,对比数值模拟和离心振动台试验结果时,数值模拟地震波采用振动台实际输出地震波,但时间间隔取0.02 s。由图14可知,尽管数值模拟所得傅里叶谱幅值在较高频率范围内(4~5 Hz)略低于试验结果,但整体而言有限元结果与试验结果接近,表明所建立的有限元模型较为合理。
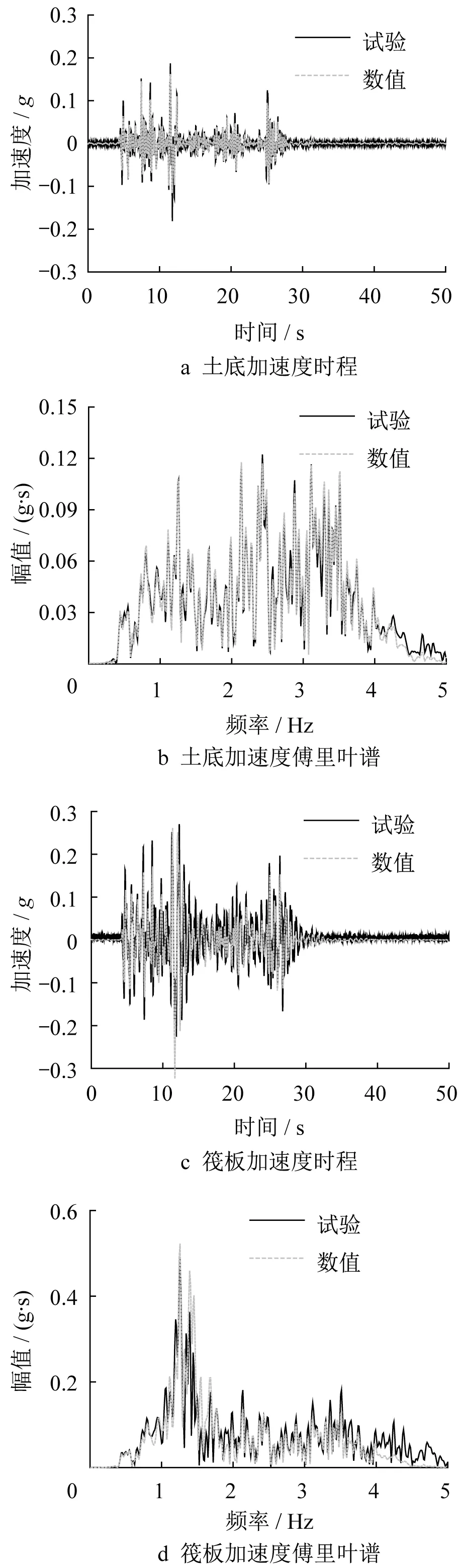
图14 数值模拟与离心振动台试验结果对比Fig.14 Comparison of numerical simulation and centrifuge shaking table test
2.3 参数分析
调整垫层隔震基础(非连接式桩筏基础)有限元模型的垫层参数,包括垫层刚度和垫层厚度,如表6所示,以分析这2个参数对垫层隔震基础地震响应的影响。作为对比,同时分析群桩基础模型有限元结果。

表6 参数分析取值Tab.6 Parameter analysis
图15为群桩基础(连接式桩筏基础)承台转角。群桩基础承台最大转角0.001 9,傅里叶谱最大幅值0.003 8,位于1.68 Hz处。图16为群桩基础模型中各桩桩位及其峰值弯矩。各桩桩顶处峰值弯矩较大,2列边桩峰值弯矩接近,中心桩与边桩及角桩峰值弯矩在埋深较浅部分差别较大,此部分受惯性作用影响较大。后续以桩4、桩5和桩6为例,分析不同工况桩身峰值弯矩。
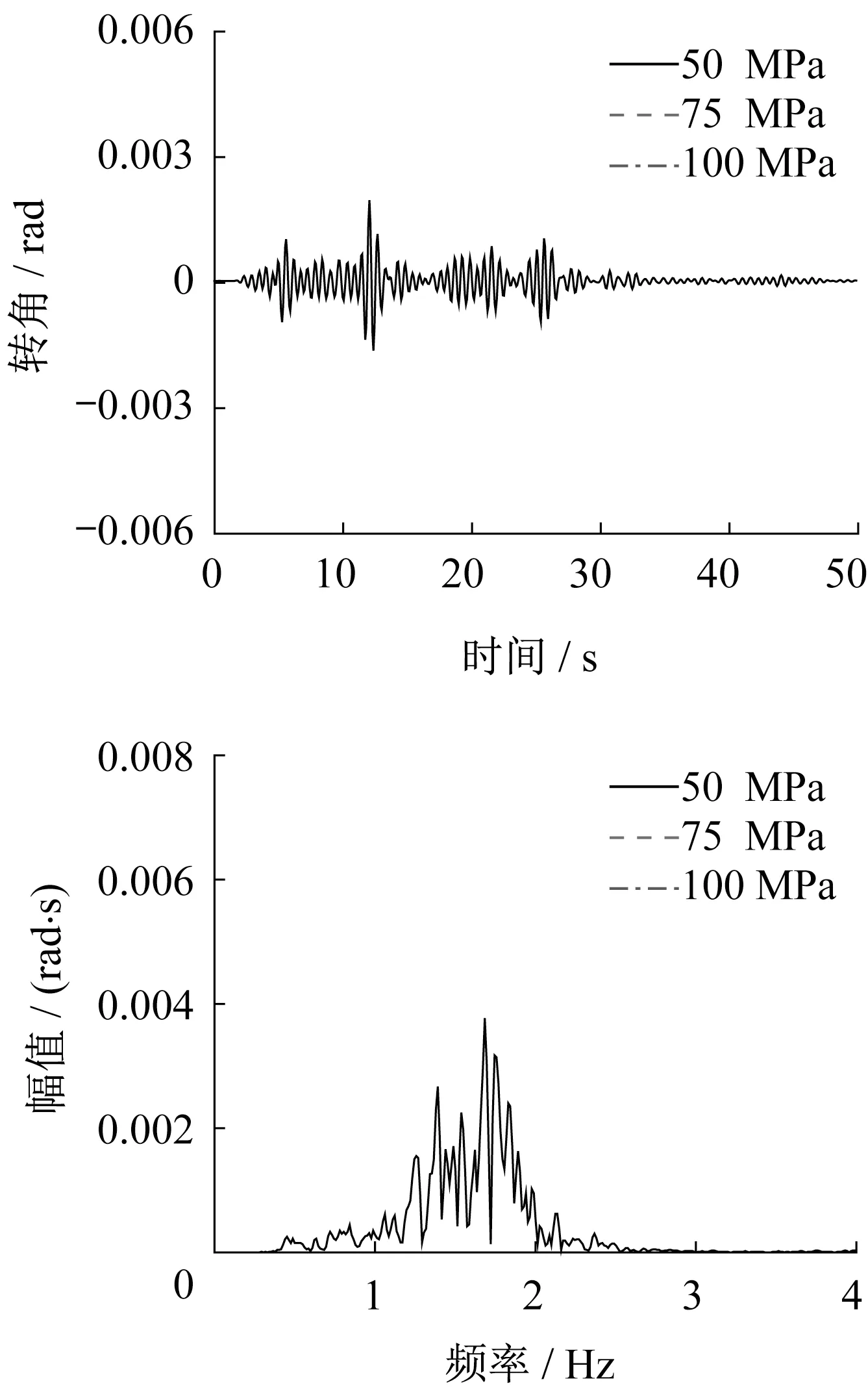
图15 承台转角Fig.15 Rotation angle of cap
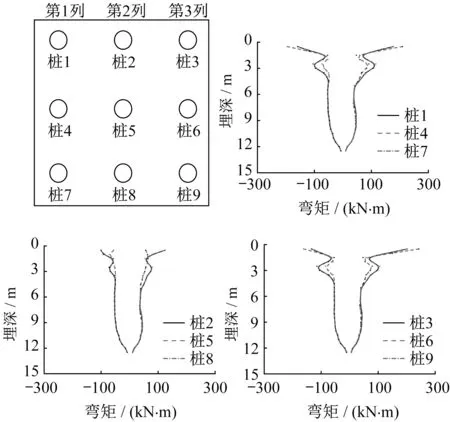
图16 群桩基础桩身弯矩Fig.16 Pile bending moment of pile group foundation
2.3.1 垫层刚度的影响
图17为不同垫层刚度的垫层隔震基础模型的筏板转角。垫层模量分别为50、75、100 MPa时,筏板最大转角分别为0.005 7、0.005 0、0.004 7rad;傅里叶谱最大峰值分别为0.006 0、0.004 9、0.004 8 rad·s,最大峰值均位于1.68 Hz处。垫层刚度增加,筏板最大转角略有降低,但仍远大于群桩基础承台最大转角;垫层模量为100 MPa时,筏板最大转角约为群桩基础承台最大转角的3倍。
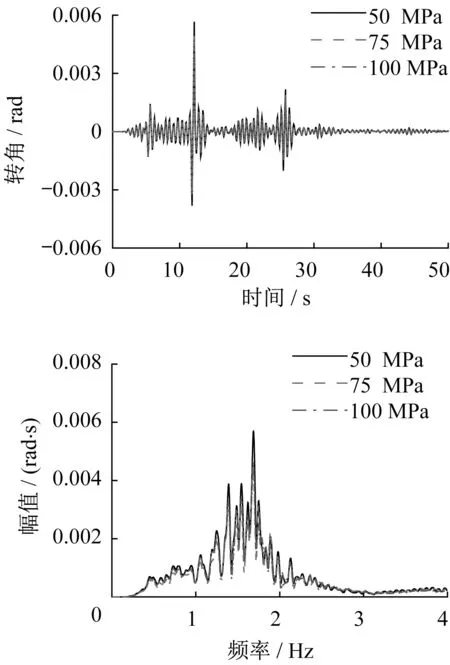
图17 不同垫层刚度的筏板转角Fig.17 Rotation angle of raft with different stiffness of cushion
图18为不同垫层刚度的垫层隔震基础模型的桩身峰值弯矩。垫层刚度为50、75、100 MPa时,桩4最大峰值弯矩分别为94.2 kN·m(-51.0kN·m)、84.5 kN·m(-50.7 kN·m)和81.4 kN·m(-54.8 kN·m);垫层刚度由50 MPa增加至100 MPa,最大峰值弯矩变化幅度在10%以内。桩5和桩6的最大峰值弯矩同样变化幅度较小,即改变垫层刚度对桩基峰值弯矩影响较小。
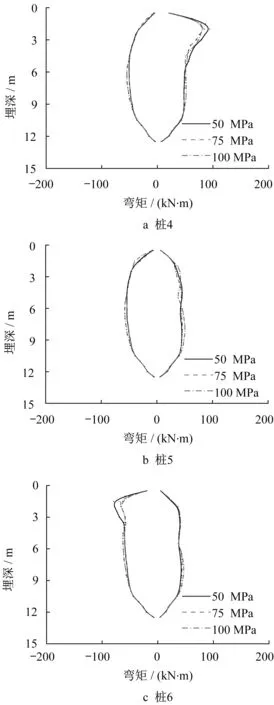
图18 不同垫层刚度的垫层隔震基础桩身弯矩Fig.18 Pile bending moment of cushioned pile raft foundation with different stiffnesses of cushion
2.3.2 垫层厚度的影响
图19为不同垫层厚度的垫层隔震基础模型的筏板转角。垫层厚度分别为0.5d(300 mm),1.0d(600 mm)和1.5d(900 mm)时,筏板最大转角分别为0.004 9、0.005 7、0.005 8 rad;傅里叶谱最大峰值分别为0.005 7、0.006 0、0.006 3 rad·s,最大峰值均位于1.68 Hz处。垫层厚度降低,筏板最大转角略有降低,但变化幅度较小;垫层厚度为0.5d时,筏板最大转角约为群桩基础承台最大转角的3倍。
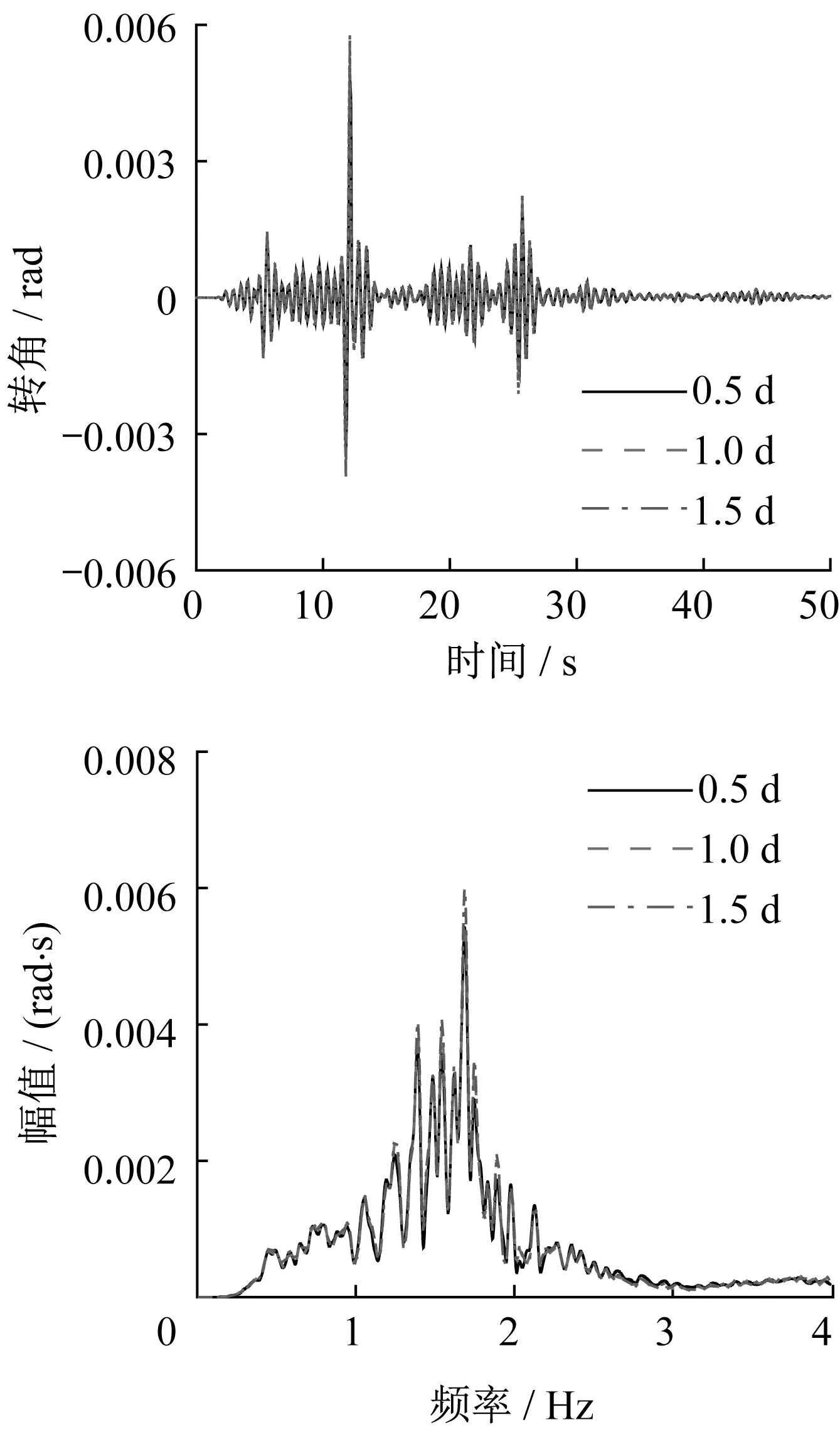
图19 不同垫层厚度的筏板转角Fig.19 Rotation angle of raft with different thicknesses of cushion
图20为不同垫层厚度的垫层隔震基础模型的桩身峰值弯矩。垫层厚度为0.5d、1.0、d1.5d时,桩4最大峰值弯矩分别为136.7 kN·m(-67.8 kN·m)、94.2 kN·m(-51.0 kN·m)和72.1 kN·m(-50.9 kN·m);桩5最大峰值弯矩分别为50.3 kN·m(-59.5 kN·m)、45.6 kN·m(-54.0 kN·m)和45.3 kN·m(-54.1 kN·m);桩6最大峰值弯矩分别为47.2 kN·m(-121.9kN·m)、42.1 kN·m(-79.2 kN·m)和42.1 kN·m(-60.9 kN·m)。垫层厚度由1.5d降低至0.5d,桩4最大峰值弯矩增加89.6%,桩5最大峰值弯矩增加11.0%,桩6最大峰值弯矩增加100.1%,即垫层厚度变化对桩身峰值弯矩的影响显著。
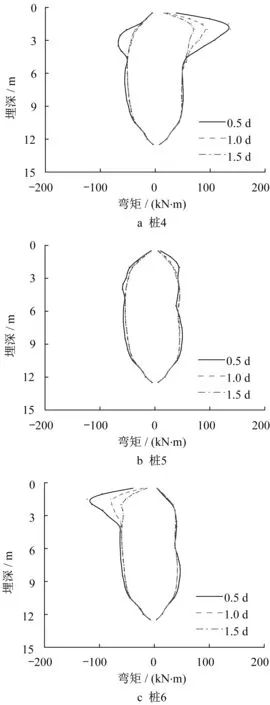
图20 不同垫层厚度的垫层隔震基础桩身弯矩Fig.20 Pile bending moment of cushioned pile raft foundation with different thicknesses of cushion
3 结论
针对砂土中的群桩基础(连接式桩筏基础)和垫层隔震基础(非连接式桩筏基础),开展了地基-基础-结构地震响应离心振动台试验和三维数值模拟,并通过对比2种基础形式的上部结构加速度和位移、筏板(承台)加速度和转角以及立柱和桩身弯矩,探讨了垫层隔震机理,分析了垫层刚度和垫层厚度等因素对垫层隔震基础地震响应的影响,得到的主要结论有:
(1)群桩基础上部结构-承台加速度传递函数峰值及其对应频率几乎不随输入地震波的变化而改变;随着输入地震波峰值的增加,垫层隔震基础上部结构-筏板加速度传递函数峰值及其对应频率却有所降低。
(2)与群桩基础相比,垫层隔震基础上部结构的峰值加速度和立柱的峰值弯矩降低,强震时分别约为群桩基础上部结构加速度峰值和立柱弯矩峰值的60%~80%,垫层隔震作用显著;强震下垫层隔震基础上部结构峰值位移增加,且残余位移较大。
(3)强震作用下垫层隔震基础筏板与垫层产生相对滑动,则与群桩基础相比,其上部结构传递至基础的惯性力降低,且桩顶约束变弱,桩身最大峰值弯矩由桩顶处转移至桩身中上部,且峰值弯矩值降低,最大弯矩峰值约为群桩基础最大弯矩峰值的50%~60%。
(4)随着垫层厚度的降低,筏板转角略有降低,而桩身最大峰值弯矩增加幅度较大,垫层厚度变化对桩身峰值弯矩影响显著;改变垫层刚度对筏板转角和桩身峰值弯矩影响较小。
作者贡献说明:
张浩:设计试验方案,构建数值模型,撰写论文。
贾亚杰:进行试验研究,开展数值分析。
梁发云:提出研究课题,指导撰写论文,审阅修订论文。
李通达:协助试验研究,处理试验数据。

