Listing Tables:a Strategy of Problem Solving in Maths from Image Thinking to Logical Reasoning
江苏常州市武进清英外国语学校 是菲菁
As is known that maths is by its nature, a creative, reflective,problem-solving activity.Maths teaching should help children to develop their skills to formulate and solve mathematical problems,as well as to evaluate the strategies and methods to be used.Today,more and more primary school maths teachers have recognized that problems solved is described as both a purpose (ability to formulate and solve problems) and as a strategy (way to acquire mathematical knowledge), even though what is a problem-solving task for one student may not be a problem-solving task for another student, their abilities of solving problems can be developed both.
However, how can primary school students develop their abilities in solving maths problems by using the problem-solving strategies effectively? Listing tables, here is taken as an example of to be discussed.
I.Step by step
The tasks of solving maths problems by using the problemsolving strategies given to the students should be designed as easy as possible so that the students can be interested in doing so,as they have achieved the successful experience by practice.Surely, the successful experience that they gained will encourage them to solve more difficult maths problems.
Example 1:
Miss Smith planted some fruit trees on her orchard.There are 3 rows of peach trees, and in each row there are 7 peach trees;there are 8 rows of apple trees, and in each row there are 6 apple trees; and there are 4 rows of pear trees, and in each row there 5 pear trees.How many fruit trees are there on her orchard in total?
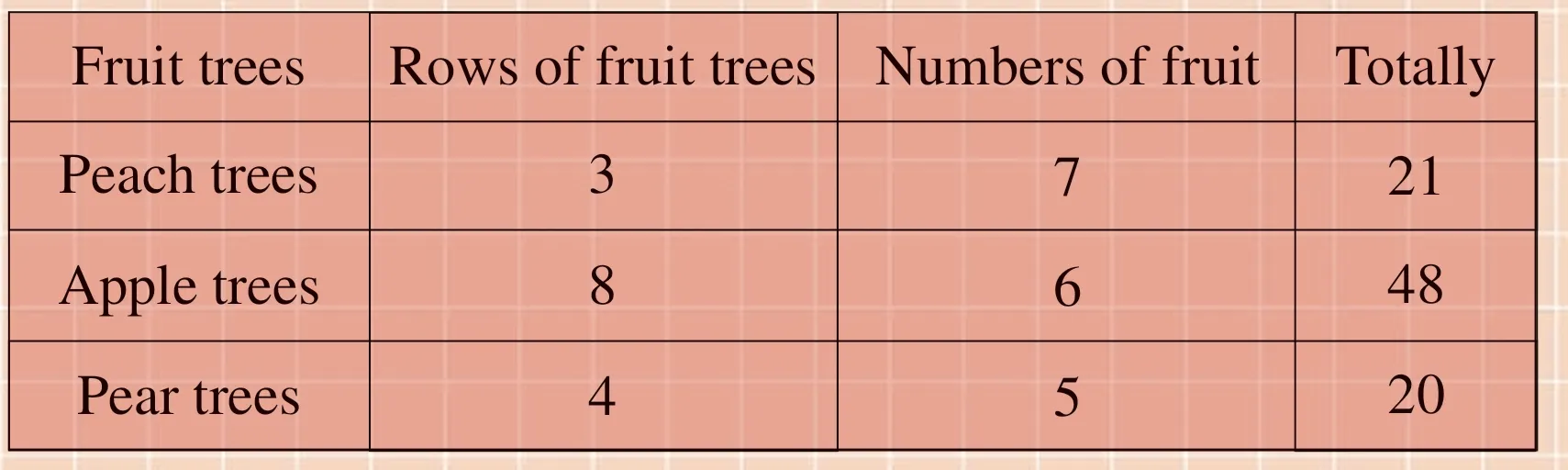
By listing a table, the students can find the answer very easily.As 3 times 7 is 21, 8 times 6 is 48, and 4 times 5 is 20, the sum of the 3 products(21, 48, and 20) is 89 trees.
Also, the table above can be turned to the table below.
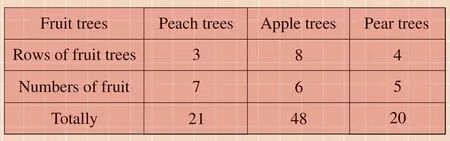
Which of the two tables is better? There is no answer.It just depends on the students’ preference.
II.Tasks designed related to the students’ life
When the students have solved some maths problems by listing tables successfully, they will have an idea to try to solve more difficult maths problems in the same way.However, only when the tasks of solving maths problems are sensible and challenging, will they be interested in solving them.
Obviously, the tasks designed must be related to the students’real life so that they meet the mental desire of the students.
Example 2:
All the 42 students in a class went boating in the park.They rented 10 boats, which were just full of them.Each big boat took 5 students and each small boat took 3 students.How many large boats and small boats did they rent?
It seems that such a hard maths problem can only be solved by using variables to represent the numbers.However, up to the time the students are reading Grade Three, they’ve never learned to write algebraic expressions, how can they do that in this way?

Luckily, the strategy of listing tables can be used.
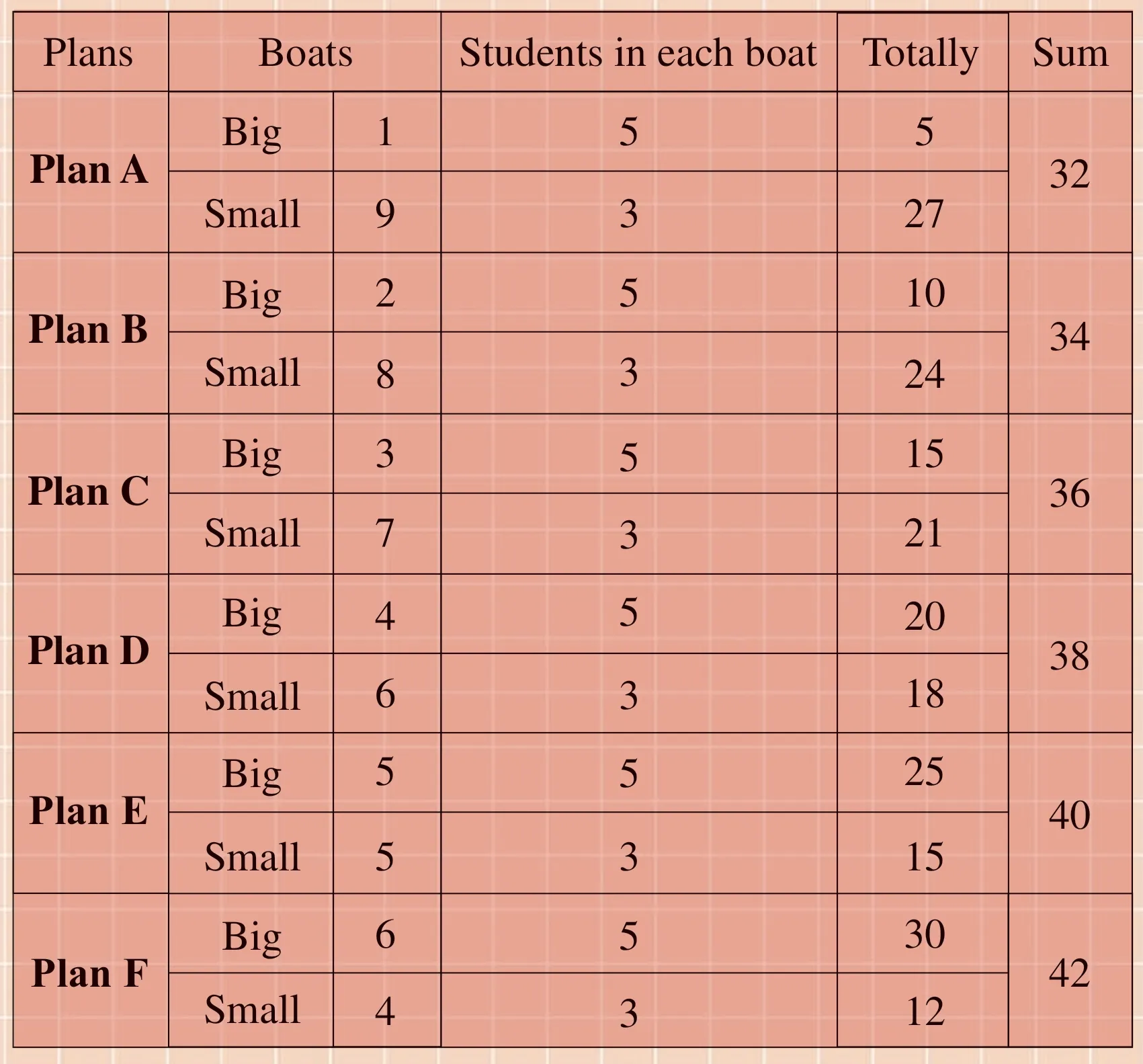
images/BZ_35_256_415_1929_1968.png
Now, the students will be surely able to find that “Plan F” is the only solution, and it is so clear to be the right answer.
Also, at least some of the students’ ability in solving such maths problems by using the strategy of listing tables will definitely develop better.To avoid wasting too much time in working out such a maths problem, they are expectedly able to choose “Plan E” first.That’s to say, they’ll divide the 10 boats into 5 small boats and another big boats first.

images/BZ_36_262_309_1935_679.png
Then, they’ll find smartly that it will be okay if the big boats are 1 more while the small boats are 1 less, as each of the big boats holds 2 students more than each of the small boats.Exactly,this observation is just “Plan F”.
III.Set up the students’ sense of relationships of pairs of numbers
To solve hard maths problems, there are several strategies to be chosen.In fact, not all the maths problems can be solved by listing tables.When the strategy of listing tables to solve maths problems is available, relationships of pairs of numbers must exist in the maths problem.
So, to develop the students’ awareness of the relationships of pairs of numbers in the maths problems must be done by maths teachers.
Example 3:
A group of students had an 8-day hiking training.They walked 140 km in 8 days.On sunny days, they walked 20 km each day; On rainy days, they walked 10 km each day.In these 8 days,how many days were sunny and how many days were rainy?
It is known that the students walked 140kmin totally during the 8 days.But how to find out how many days were rainy and how many days were sunny? To solve this maths problem, maths teachers must lead their students to focus on the relationships of pairs of numbers in the maths problems first, or they can hardly list a right table.Definitely, there are 3 pairs of related numbers in this problem.
Pair 1: 8 days /140km
Pair 2: ? sunny days / ?km
Pair 3: ? rainy days / ?km
As the relationships of pairs of numbers are set up, the students list a table easily now.(Prepresents possibility;Rrepresents rainy days;Srepresents sunny days; andDrepresents days.)
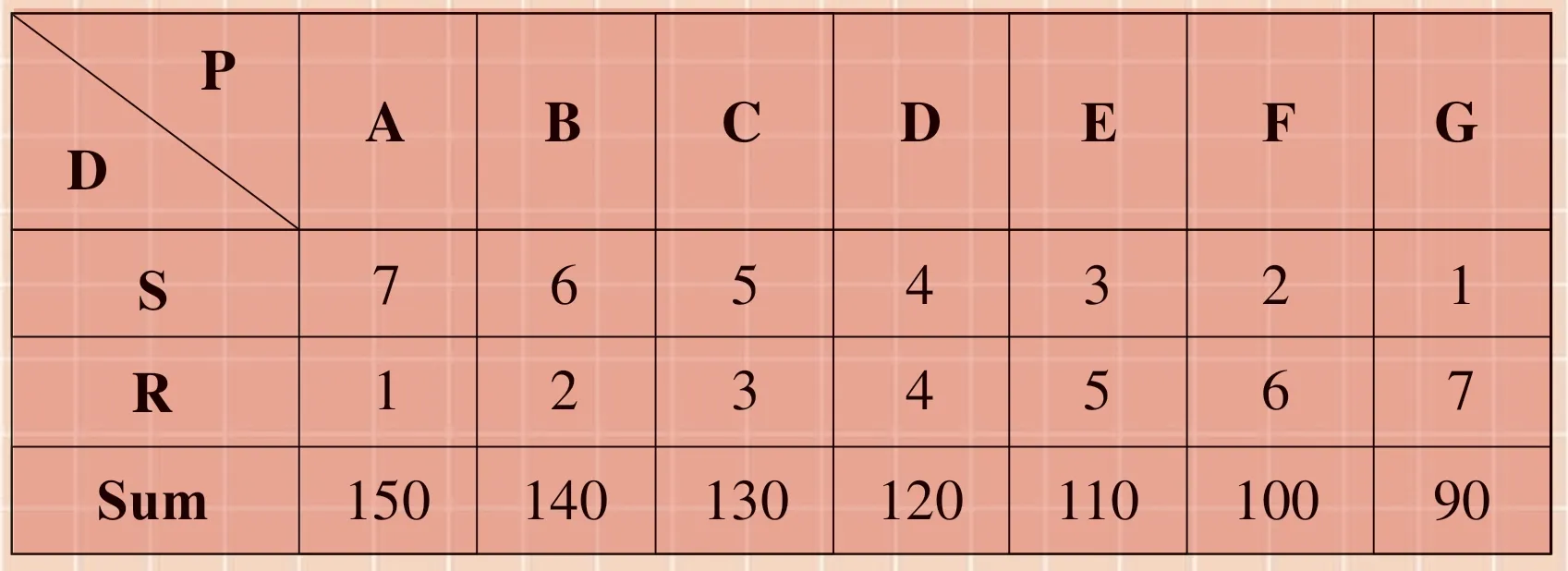
D P A B C D E F G S R Sum 7 6 5 4 3 2 1 1 2 3 4 5 6 7 150 140 130 120 110 100 90
This table is listed so clearly that the students will be able to find the solution by this way.

