依托几何直观 理解意义本质

【摘要】本文以“一个数除以分数”的教学为例，论述借助几何直观帮助学生理解算理和掌握算法的方法，建议教师在深刻解读教材的基础上，设置课堂前测环节，基于学生学情，在具体的教学题境中借助几何直观帮助学生更好理解算理、掌握算法，从而优化教学效果。

【关键词】小学数学 几何直观 意义本质

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2021）13-0142-04

人教版小学数学六年级上册第三单元《分数除法》第三课时“一个数除以分数”的计算教学是小学数学教学的重点与难点。如何让学生形象理解“除以一个分数，等于乘这个分数的倒数”的算理呢？笔者在实践中发现，学生掌握和运用计算方法相对而言比较容易，然而在理解算理方面遇到了比较大的困难。那么，学生学习“一个数除以分数”的知识储备和认知起点是怎样的？它的教学目标应该如何定位？它的计算教学到底关注点在哪里？笔者认为，有必要对学生关于“一个数除以分数”的认知水平做一次前测，以便更好地进行教学。下面，笔者结合多教材的对比沟通，基于学生基础，试图在具体的教学题境中借助几何直观帮助学生更好地理解算理、掌握算法，优化教学效果。

一、教材解读

以生为本，关注学生生活经验和认知基础是教学本课需要贯彻的原则。学生在学习“一个数除以分数”之前，到底有怎样的逻辑起点和现实起点？这正是教师首先要考虑的问题。笔者拜读了省数学特级教师袁晓萍、吕立峰的相关文章，发现针对不同的学生需要不同的学习过程，有些策略即使很好，也可能不适合本班学生，不能全部照搬。针对该教学内容，笔者研读了几套不同版本的教材，发现编委的意图均有所侧重，各不相同。

北师大版教材将这部分内容安排在五年级下册第五单元，它通过平均分4个同样大的饼的问题情境，让学生直觀感受“一个数除以分数”的意义理解。浙教版教材同样将此内容安排在五年级下册，让学生在学习分数乘法的基础上紧接着学习分数除法，教材借助一条绸带，让学生直观理解同分母分数除法的意义，同时教材突出了算法的重要性，有刻意回避“一个数除以分数”的算理之嫌。苏教版教材以3个不同的平均分的问题情境，借助格子图和彩带图，利用数形结合思想帮助学生理解“一个数除以分数”的算理。人教版教材则呈现了学生熟知的行程问题。

针对不同教材同一内容的呈现，结合人教版教材，笔者设计了如下前测对学生的学情基础进行调查。

调查问卷（前测）

班级：       姓名：

亲爱的同学，老师想了解你在分数除法学习过程中的情况，请你按要求认真回答以下问题。记住，独立完成哦！

问题1：3÷[12]=

（1）你会算吗？（  ）A.会  B.不会

（2）如果你会算，那么请你用自己想到的方法进行计算。写一写、画一画，你是怎么想的？

问题2：小明[310]小时行了[910]千米，他每小时行了多少千米？

（1）你能列出算式来解决这个问题吗？（  ）

（2）上面的算式你会计算吗？请你用自己想到的方法进行计算。写一写、画一画，你是怎么想的？

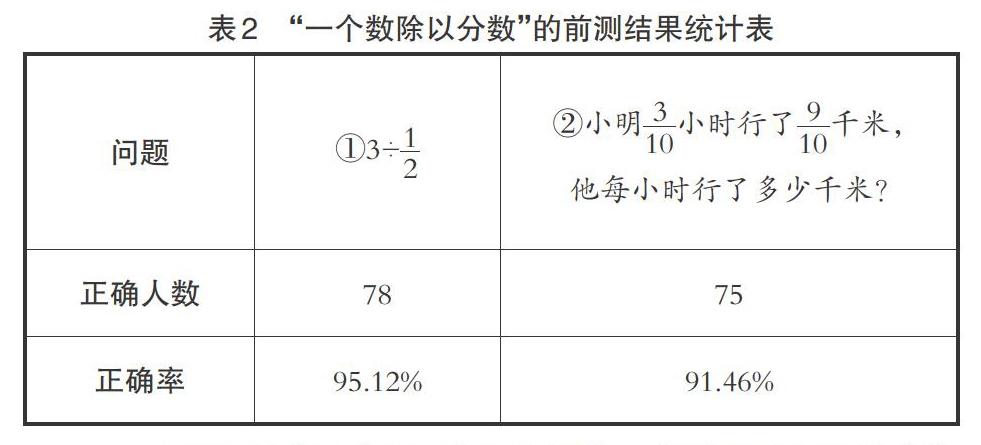
前测的两个问题分别指向“整数除以分数”和“同分母分数除法”的教学内容。教学前一天，笔者随机调查了本年级两个班共82名学生。通过调查发现，两个问题的计算正确率均达到了90%以上。

通过调查，笔者还发现，学生在解决这类题目时所用的计算方法多样，从图形的描述中也能基本看出学生对算理的理解是比较清晰的。基于这样的学生基础，初步敲定了本节课的教学流程，并制订了课时目标。笔者简单通过前测巩固理解“整数除以分数”和“同分母分数除法”两种计算题的意义，把异分母分数除法作为本节课的重点进行教学。通过环环相扣、层层推进的流程，基于同分母分数除法，打通异分母分数除法，从而帮助学生更好地理解分数除法的算理，使学习最优化。

教学流程

基于前测3÷[12]，理解“整数除以分数”的算法和算理

题境互译[910]÷[310]，掌握“同分母分数除法”的计算意义

类比迁移[95]÷[310]，巩固“异分母分数除法”的法理相通

归纳“一个数除以分数”的算法

二、教学实践

基于学生的现实起点和逻辑起点，重组“一个数除以分数”的教学设计，以此优化学生对此计算的意义理解，促进算法和算理的真正沟通，达到深度学习的目的。

（一）基于前测，理解“整数除以分数”的算法和算理

【片段一】

1.出示题目，自主探索

前测题目1：3÷[12]

师：同学们，课前我们进行了两道题目的练习，这是第一个题目（出示问题1），答案是几？猜一猜咱们班的正确率是多少？（39÷41≈95.12%）

师：正确率这么高，那你们再猜一下，解决这道计算题，我们班一共有多少种做法？我们一起看看吧。

2.作品展示，互动交流

方法一：乘倒数

师：第一种方法是同学们用得最多的，请×××同学说说想法。

生：我们知道，除以一个数就等于乘这个数的倒数，所以3÷[12]=3×2=6。

师：评价一下他的方法怎么样？

（板书方法）

方法二：商不变性质

师：我们来看这种方法，你看懂了吗？

出示：3÷[12]=（3×2）÷（[12]×2）=6÷1=6

生：我们把被除数和除数同时乘2，利用以前学过的商不变性质，这样就变成了6÷1=6，所以3÷[12]=6。

师：大家都听明白了吗？这是把分数除法转化成  ？

生：把分数除法转化成整数除法来计算。

师：你评价一下他的方法怎么样？同学们利用商不变性质方法可以吗？

（板书方法）

方法三：分数与除法的关系

师：再来看第三种，请×××同学来说。

出示：3÷[12]=3÷（1÷2）=3÷1×2=6

生：我们以前学过分数与除法的关系，[12]=1÷2，所以3÷[12]=3÷（1÷2）=3÷1×2=6。

师：利用分数与除法的关系，我们把这样的分数除法转化成整数除法来计算，确实是一种好办法。

（板书方法）

方法四：分数化小数

师：再来看第四种，请×××同学来说。

生：我们可以把[12]化成小数0.5，然后3÷[12]=3÷0.5=6。

师：把分数除法转化成小数除法来计算，很不错哦。

（板书方法）

方法五：画图形

师：再来看第五种，画图来解释计算，请×××同学来说。

生：我先画3个圆代表3，画半个圆代表二分之一，再把3个圆都平均分成两份，一共就有这样的6个半圆，6个半圆刚好是1个半圆的6倍。

师：你是把分数除法转化成   ？

生：我是把分数除法转化成画图来计算的。

师：利用画图的方法也是可行的。

（板书方法）

方法六：线段图

师：再来看第六种，画线段图来解释计算，请×××同学来说。

生1：我先画3条线段代表3，再画半条线段代表二分之一，把3条线段都平均分成2份，一共就有这样的6个半条线段，所以是6倍。

师：谁听明白了？

生2：他是把分数除法转化成线段图来计算的。

师：听明白了吗？这里单位1是什么？为什么要平均分成2份？最后这个计算就是在求什么？

数的转化

形的转化

3.对比沟通，适当概括

师：同学们，原来可以有这么多方法，你想到了吗？我们不但可以从数的角度，也可以从图形的角度来考虑解决这个问题，都是将新的知识转化成已经学过的知识。看来，集体的智慧就是强大，给聪明的自己鼓鼓掌吧。

（二）题境互译，掌握“同分母分数除法”的计算意义

【片段二】

1.出示题目，进行探索

前测题目2：小明[310]小时行了[910]千米，他每小时行了多少千米？

师：我们来看一下，这道题你当时是怎么列式解决的？

生：[910]÷[310]。

师：是的，我们也来看一下，这道计算题，我们班的同学是怎么解决的？

2.作品展示，互动交流

（依次出示学生的计算方法，简单交流）

方法一：[910]÷[310]=[910][×103]=3（千米/时）

方法二：[910]÷[310]=（[910]×10）÷（[310]×10）=9÷3=3（千米/时）

方法三：[910]÷[310]=0.9÷0.3=3（千米/时）

方法四：

师：有的同学用了这样一个线段图来解释计算，你看懂了吗？

生：这里的一条线段就表示1小时，把它平均分成10份，每一份就是[110]小时，这样的3份就是[310]小时。根据题目意思，[310]小时行了[910]千米，从线段图上我们可以很清楚地看到，1份也就是[110]小时行了[910]千米÷3，也就是[310]千米。然后1小时有这样的10个[110]小时，也就是[310]千米×10=3千米。所以说，小明[310]小时行了[910]千米，他每小時行了3千米。

师：同学们，你们听明白了吗？

（教师此时再请一名学生说一遍，并根据学生说的及时形成板书）

板书：[910]÷[310]=[910]÷3×10=[910]×[13]×10=[910×103]=3（千米/时）

3.对比沟通，内在求联

师：同学们，我们不但用了这么多的方法来计算[910]÷[310]，更可贵的是我们还发现了它们之间的内在联系，大家真的很厉害。

（三）类比迁移，巩固“异分母分数除法”的法理相通

【片段三】

1.出示题目，有效探索

题目：小丁[310]小时行了[95]千米，他每小时行了多少千米？

师：同学们，这个问题又该怎么解决呢？它和刚才的算式不一样在哪里？你会计算吗？

出示合作要求：在作业纸上画一画、写一写，做完后四人小组说一说做法。

2.操作交流，内化算法

方法一：[95]÷[310]=[95×103]=6（千米/时）

方法二：

3.对比沟通，自然求联

师：[95]×[13]是什么意思？你能用粉笔表示求的这一部分吗？再乘10是什么意思？同学们请看这一步。

生：就是乘倒数。

师：是啊，所以线段图其实就是在帮助解释“为什么除以一个数等于乘这个数的倒数”。

板书：[95]÷[310]=[95]÷3×10=[95]×[13]×10=[95×][103]=6（千米/时）

师（小结）：同学们，乘倒数这么受大家喜欢是因为它简单实用，它就是分数除法的计算方法。线段图是对算法的一种解释，是算法背后的算理，为我们解释了分数除法的原理。

三、课后思考

本节课的教学，充分借助几何直观，降低思维难度，让学生在形象感知的基础上理解“一个数除以分数”的抽象意义，进一步掌握算法、理法通融。

（一）依托几何直观，意义理解应景而生

《义务教育数学课程标准》（2011年版）（以下简称“课标”）指出：几何直观主要是指利用图形描述和分析问题，借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。课标通过阐述几何直观的本质，非常清楚地揭示了几何直观的重要性和必要性。几何直观是数学计算教学中必不可少的有效工具。

通过本节课的前测，笔者发现学生基本掌握了“整数除以分数”和“同分母分数除法”类的计算题的算法。学生想到了用6种方法解决3÷[12]和[910]÷[310]。基于这样的学生基础，笔者在课始就出示学生的学前情况，通过题境“小明[310]小时行了[910]千米，他每小时行了多少千米”让学生充分理解[910]÷[310]=[910]÷3×10=[910]×[13]×10=[910]×[103]=3的计算过程，然后在此基础上通过“小丁[310]小时行了[95]千米，他每小时行了多少千米”这个题境慢慢推进“异分母分数除法”的意义理解，层次清楚，有效突破了“除以一个数等于乘这个数的倒数”的教学难点，从而促进学生对知识的深度学习。

（二）依托几何直观，知识体系自然求联

从教材体系中，我们不难发现，整数除以分数会用到分数除以整数算法的经验，如教学3÷[12]时，学生想到的种种方法都是可以用包含除的意义去解决的，即3÷[12]就是表示3里面有几个[12]。以此类推，同分母分数除法、异分母分数除法如果用这个方法去解决，表面上看似没有问题，实质上却和题目的意义（速度时间路程）有了矛盾。

那么，究竟应该怎样缓解这对矛盾，沟通新旧知识的联系，在新旧知识的连接点上发展新知，打通知识关联的体系？本节课在探索“一个数除以分数”的计算方法中，教师充分借助线段图，帮助学生进行自主探索，学生在具体可见的线段图中对“除以一个数等于乘这个数的倒数”的计算法则有了直观的理解。通过不断地表达、质疑，让学生在充分理解“除以一个数等于乘这个数的倒数”的算理的基础上，掌握法則，驱动学生从“算法”走向“算理”，进而打通了三类分数除法计算题之间的内在联系。

（三）依托几何直观，数形之间有机结合

数形结合思想是一种重要的数学思想方法。著名数学家华罗庚非常重视“数形结合”，他认为：数无形是少直觉，形少数时难入微，数形结合百般好，隔离分家万事休。借助直观形象模型理解抽象的数学概念，体会数学计算的意义，显然是小学生学习数学的重要方法。

在本节课[95]÷[310]的教学中，笔者借助线段图，让学生在自主探索中发现，这里的一条线段就表示1小时，把它平均分成10份，每一份就是[110]小时，这样的3份就是[310]小时。根据题目意思，[310]小时行了[95]千米，从线段图上可以很清楚地看到，1份也就是[110]小时行了[95]千米÷3，也就是[35]千米。然后1小时有这样的10个[110]小时，也就是[35]千米×10=6千米。所以说，小明[310]小时行了[95]千米，他每小时行了6千米。借助线段图来理解算法，让学生知其然，更知其所以然，让学生的思维在整个几何直观的理解中走向深度，从而促进学生对分数除法意义的深入理解，同时巩固算法。

【参考文献】

[1]葛敏辉.分数除法计算教学研究[M].杭州：浙江教育出版社，2018.

[2]吕立峰，郭春.读懂学生，读透教材，让学生真实发生——“分数除法”单元整合课的研究历程[J].小学数学教育，2020（1-2）.

[3]袁晓萍.“分数乘、除法”单元重组的思路与课时划分[J].小学数学教育，2020（1-2）.

[4]刘颖.几何直观在小学数学计算教学中的应用策略[J].小学数学教育，2020（5）.

[5]顾晓东.数形结合思想的内涵意蕴及培养策略[J].教学月刊，2020（6）.

【作者简介】袁春胭，浙江省杭州市滨江实验小学数学教师，大学本科学历，一级教师，杭州市教坛新秀、区优秀人民教师、区名师名校长培养对象，主要从事教师队伍建设、学科教学与教育研究。

（责编 杨 春）