盾构隧道带榫环缝受力和变形修正计算方法
李明宇,吴龙骥,赵世永,靳军伟
(1.郑州大学土木工程学院,河南 郑州 450001;2.中铁十五局集团有限公司,上海 200070;3.中铁十五局集团城市轨道交通工程有限公司,河南 洛阳 471000)
盾构隧道是由管片与接缝构成的一个非连续的空间组合结构,接缝处通常采用螺栓连接,其刚度远小于管片,在受力后往往会产生相对较大变形,严重时将引发接缝渗漏和管片破损等病害。系统分析环缝受力和变形特征,对其构造合理优化,避免或减少大变形的发生,对于盾构隧道病害防治具有重要意义。
近年来,针对盾构隧道纵向不均匀受力变形和接缝处受力变形的研究日趋增多,璩继立[1]利用布辛奈斯克解求出隧道上部的附加应力,并求出隧道的纵向位移和内力。柯宅邦[2]、康成[3]、张勇[4]将隧道等效为梁模型,给出了地面堆载时盾构隧道纵向变形的线性解析解、非线性解析解。吴怀娜[5]、刘波[6]分别针对隧道实际剪切错台变形的特点,将隧道简化为均匀的铁木辛柯梁,提出了一种新的考虑环间剪切位错的纵向结构模型。叶飞等[7-9]分别考虑横向刚度和变形的影响,进一步对盾构隧道纵向等效抗弯刚度进行了修正计算分析。对于接缝处的受力变形研究,李守巨[10]通过理论分析给出了受拉区螺栓应力和受压区高度与衬砌管片极限应变之间的关系,陈代秉[11]对管片横纵向连接螺栓、螺栓预加力和螺栓安装扭矩等设计计算理论和方法进行了探讨。何川[12]通过解析推导证明了环接头的固有非线性,得到了不同载荷作用下环接头三维表面的刚度,提出了一种基于内力的环节点刚度迭代算法。
对于以往研究进行总结可以发现,目前对于盾构隧道纵向变形问题的理论计算分析主要采用弹性地基梁或修正弹性地基梁理论,以及纵向等效刚度或修正纵向等效刚度理论,但是这两种理论在实际计算应用时都存在缺陷。对于双参数弹性地基梁模型而言,以往文献利用该模型计算时,未将盾构隧道纵向刚度有效率考虑其中;而对于修正纵向等效刚度模型而言,计算环缝处管片和螺栓应力和变形时,该处的弯矩、剪力和轴力均是人为设定的,其与作用于隧道上的附加作用力大小与分布形式均无关。
为了解决上述问题,笔者在已有研究基础之上,对两种理论计算模型进行了进一步修正,同时将两者结合,首先分析了均布荷载作用下盾构隧道纵向弯矩与剪力分布特征、带榫环缝错台变形特征及其演化过程中纵向螺栓的受力特点;其次,根据纵向螺栓的受力情况,对凹凸榫尺寸变化及纵向螺栓预紧力影响下环缝处错台量和张开量的界限值进行了探讨。通过研究可以进一步推动盾构隧道纵向变形计算理论的发展,同时为地铁盾构隧病害防治提供理论依据。
1 双面弹性地基梁与纵向等效连续化模型的组建与修正计算
1.1 双面弹性地基梁修正微分方程
在实际工程中,环缝的存在往往削弱了盾构隧道纵向抗弯刚度,以往在使用双面弹性地基梁模拟隧道进行计算时,均未考虑纵向刚度折减系数η,已有专家学者通过试验等方法确定纵向刚度折减系数η为0.2左右[13-14],笔者引入纵向刚度折减系数η,修正公式如下:
ω(4)+4λ4ω=qη/EI.
(1)
式中:λ为地基柔度系数,1/m。
(2)
式中:K1、K2为集中基床系数,kN/m2,K1=k1B、K2=k2B,B为隧道结构的底面宽度,m;k1、k2为下、上基床系数,kN/m3。
1.2 局部荷载下双面弹性地基梁修正计算
无限长双面弹性地基梁受局部均布超载作用的物理模型如图1所示。隧道结构任意位置m至n范围内作用均布荷载q,在隧道任意位置r处建立局部直角坐标系x1-o-ω1。

图1 双面弹性地基梁局部均布荷载作用示意图Fig.1 Schematic diagram of local uniformly distributed load action of double-sided elastic foundation beam
经计算得出梁的挠度ω,同时可以得出在双面弹性地基梁上任意位置m至n作用局部均布荷载q时弯矩M、剪力Q。
1.3 纵向等效抗弯刚度修正计算
笔者考虑横向变形、纵向螺栓预紧力对纵向抗弯刚度的影响。可以得到纵向连接螺栓处于弹性受力状态时隧道纵向等效抗弯刚度为[15]
(3)
式中:E为管片衬砌的弹性模量,MPa;I为衬砌环横截面惯性矩,m4;l为环宽,m;lα为环缝影响范围的长度,m;lβ为纵向连接螺栓的长度,m。
考虑纵向连接螺栓预紧力时,纵向连接螺栓最大拉应力为
(4)
式中:kj1为单个纵向连接螺栓的弹性刚度,kN/m3;δj为距离中性轴最远处的环缝张开量,mm;μ为纵向螺栓预紧力损失系数;Ps为纵向连接螺栓预紧力,kN;Aβ为纵向连接螺栓的横截面面积,m2。
1.4 修正双面弹性地基梁-纵向等效连续模型
对于纵向等效连续化模型,在得到纵向连接螺栓受弯引起的拉应力的过程中所用到的弯矩是假设的,而双面弹性地基梁经过计算可以提供弯矩,可以将两者有机结合起来。将双面弹性地基梁得到的弯矩式(3)代入式(6)即可求出纵向连接螺栓受弯引起的拉应力。
2 环缝受剪时纵向螺栓受力计算
随着环缝变形的发展,纵向连接螺栓将同时抵抗弯矩、拉力、剪力三种外力作用。笔者对环缝错台过程中纵向连接螺栓受力过程进行分析。
环间变形发展不同阶段纵向连接螺栓的受力和变形状态如图1所示。力学分析时假定纵向连接螺栓两端为固定约束。
将纵向螺栓受力变形分为四个阶段:第一阶段如图2(a)所示为初始阶段,即在连接螺栓两端施加预紧力;第二阶段如图2(b)所示,此时环间发生错台,未产生张角;第三阶段如图2(c)所示,此时凹凸榫面产生接触滑移,环间同时出现张开和错台,但螺栓孔空隙未闭合,螺栓不受剪;第四阶段如图2(d)所示,在第三阶段的基础上,螺栓孔与螺栓开始接触产生相互作用。

图2 纵向螺栓受力分析图Fig.2 Force analysis diagram of longitudinal bolts
对于第一阶段,螺栓两侧轴向拉应力为
(5)
对于第二阶段,错台量δ1小于凹凸榫间的物理间隙δs,此时纵向连接螺栓的最大拉应力和最大剪切应力为
(6)
(7)
式中:d为纵向连接螺栓直径,mm;x为以A为计算原点,纵向螺栓上任意位置到A的距离,mm,0≤x≤lβ;Eβ为连接螺栓弹性模量,MPa;Iβ为螺栓的截面惯性矩,mm4;δ1凹凸榫面接触前的错台量,mm。
对于第三阶段,凹凸榫面产生接触滑移,环间同时出现张开和错台,但螺栓孔空隙未闭合,螺栓不受剪,此时纵向连接螺栓的最大拉应力和最大剪切应力为
(8)
(9)
式中:δ2为凹凸榫面滑移后环间的错台量,mm;Δ为环间张开量,Δ=ls(δ2-δ1)/lh,其中ls、lh分别为凹凸榫的宽度和高度。
对于第四阶段,榫面间的相对滑动致使螺栓孔与螺栓开始接触产生相互作用,假设纵向连接螺栓不均匀受力,受到剪切力作用的螺栓为n个,引入剪力分配系数Cq(定义为纵向连接螺栓所承担的总剪力nQl与环断面总剪力(Q-f)的比值),由于环面已分离,可认为摩擦力f=0,此时有凹凸榫所承担的剪力Qs和单个螺栓承担的剪力Ql分别为
Qs=(1-Cq)Q.
(10)
(11)
当此时的环间错台量δ3与螺栓孔的物理间隙δl相等时,剪力分配系数Cq取0;当环间的错台量δ3大于等于凹凸榫的物理间隙δs与凹凸榫高度lh之和时,此时连接螺栓承担全部的剪力,根据文中提出的剪力分配系数定义,此时剪力分配系数Cq取1;当δl<δ3<δs+lh时,通过线性插值确定分配系数Cq。
当凹凸榫面未分离时,即δl<δ3<δs+lh,纵向连接螺栓的内力如图3所示。
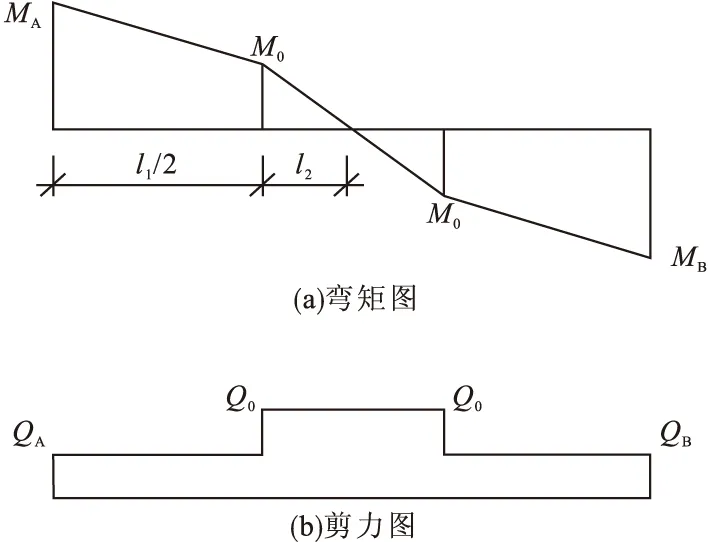
图3 图2(d)中纵向螺栓内力图Fig.3 Longitudinal bolt internal force diagram in figure 2(d)
此时纵向连接螺栓的最大拉应力和最大剪切应力如下。

(12)
(13)
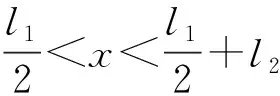
(14)
(15)

(16)
(17)

通过图4计算出连接螺栓各处的弯矩与剪力:
(18)
当凹凸榫面分离时,即δ3≥δs+lh,此时凹凸榫不受剪,纵向连接螺栓受剪,承担全部的剪力,此时剪力分配系数Cq取1,纵向连接螺栓的最大拉应力和最大剪切应力与凹凸榫面未分离时推导过程相同。
通过前文研究结果可知,螺栓的最大拉应力和最大切应力分别为

(19)

3 实例分析
3.1 工程实例
以某盾构隧道(局部19 m)作用局部荷载q=372.94 kN/m(距离原点距离分别为5 m、24 m)时为例,对衬砌接缝处进行受力分析。
根据现场资料,隧道外径D为6.2 m,内径D0为5.5 m,管片厚度t为0.35 m,环宽为1.5 m,管片弹模E为34 500 MPa,根据A.S.Vesic[16]提出的置于地表上的长梁地基反力系数表达式,取基床系数K为6.0×104kN/m3,纵向刚度折减系数η取0.2。纵向连接螺栓个数n为17个,螺栓弹模Eβ为2.1×105MPa,螺栓长度lβ为40 cm,螺栓直径d为30 mm。衬砌接缝处参数见表1。

表1 衬砌接缝处参数Table 1 Parameters of lining joints
由于缺乏收敛监测数据,在计算时取长半轴与短半轴相等,均为3.1 m。将相关数据带入前文推导的公式进行计算,隧道纵向任意截面处的弯矩和剪力如图4所示,从图中可以得出,最大弯矩Mmax=1 683 kN·m,最大剪力Qmax=615.5 kN。带入式(19)得到纵向连接螺栓最大拉应力σmax=71.206×105kPa,大于纵向连接螺栓的设计的受拉屈服强度6.4×105kPa。纵向连接螺栓的最大切应力为3.544×104kPa,小于纵向连接螺栓的设计的受剪屈服强度1.5×105kPa。通过计算得到的纵向连接螺栓还没有受剪屈服但已受拉屈服,因此选择纵向螺栓受拉屈服强度作为环间变形控制指标比选择纵向螺栓抗拉屈服强度作为环间变形控制指标更加安全。

图4 剪力弯矩计算结果Fig.4 Calculation results of shear moment
为了验证以纵向螺栓受拉屈服强度作为评判依据的可靠性,现将相关参数带入可计算接缝处错台张角的铁木辛柯梁模型[17]也可计算接缝处错台转角量,其变形分布曲线如图5、图6所示。

图5 盾构隧道纵向张开量分布Fig.5 Longitudinal opening distribution of shield tunnel

图6 盾构隧道纵向错台量分布Fig.6 Distribution of longitudinal displacement of shield tunnel
通过计算得到错台量δmax=4.331 mm,小于现场实测得到的最大错台量δ2=12 mm及地铁隧道设计要求接缝的环间错台量界限值15 mm[18],与基于铁木辛柯梁模型计算得到的最大错台量3.987 mm相近。张开量Δmax=0.441 mm,小于现场实测得到的最大张开量0.6 mm及地铁隧道设计要求接缝的张开界限值2 mm,与基于铁木辛柯梁模型计算得到的最大张开量0.392 mm相近。
3.2 参数影响分析
考虑凹凸榫间的物理间隙δs、凹凸榫结构的宽度ls、高度lh和连接螺栓的预紧力Ps对连接螺栓受拉屈服时环间变形量的影响,进行参数灵敏度分析。图7所示为凹凸榫间的物理间隙δs、凹凸榫结构的宽度ls、高度lh和连接螺栓的预紧力Ps与环间张开量界限值Δt、错台量界限值δt的关系曲线。

图7 环间变形量影响因素参数分析Fig.7 Parameter analysis of influencing factors of deformation between rings of shield tunnel
由图7可知,凹凸榫间的物理间隙与环间错台量、张开量界限值关系密切,环间错台量界限值与凹凸榫间物理间隙表现为同方向、线性关系变化;环间张开量界限值与凹凸榫间物理间隙表现为反方向、线性关系变化。凹凸榫宽度、高度对环间错台量、张开量界限值影响不大。螺栓预紧力对环间错台量影响微小,与张开量界限值关系密切,随着螺栓预紧力的增大,环间张开量呈线性减小。
4 结 论
(1)提出了一种盾构隧道带榫环缝处受力变形的计算方法,该方法不仅能体现外荷载大小与作用形式对衬砌结构带榫环缝处纵向螺栓受力的影响,而且能反映出带榫环缝错台的演化规律及其变化过程中纵向连接螺栓的受力特征以及凹凸榫尺寸对环缝处错台量和张开量的界限值设置的影响。
(2)当盾构隧道结构参数与本计算模型相近时,以纵向螺栓受拉屈服强度作为评判标准计算得到的错台、张开值小于工程实测及验收标准规定的界限值,因此以纵向连接螺栓受拉屈服强度作为环间变形控制指标是可行的。
(3)若以纵向连接螺栓的抗拉强度为计算依据,环间错台量界限值δt和张开量界限值Δt对于凹凸榫间的物理间隙δs的变化最为敏感,螺栓预紧力对环间张开量影响较大,但对错台量几乎没有影响,凹凸榫的宽度和高度对环间界限错台和张开量的影响很小。

