盾构隧道斜螺栓连接环缝剪切破坏特征理论解析
何 源, 杨振华, 柳 献, *, 丁文其
(1. 中交二航局第三工程有限公司, 江苏 镇江 212000; 2. 同济大学, 上海 200092)
0 引言
工程实践表明,在盾构隧道沿纵向不均匀沉降的过程中,管片本体的变形很小,变形主要集中在环缝附近。另一方面,环缝是一类由螺栓连接的不连续构件,其强度远远低于管片本体,其承载能力直接决定隧道的承载能力。为了提高隧道的正常使用性能和极限承载能力,有必要研究盾构隧道环缝的受力性能及其破坏机制。
现有盾构隧道环缝受力性能的研究主要分为2类,部分学者采用解析解法对环缝的受力性能展开研究。志波由纪夫[1]给出了1组公式,用于计算环缝的抗弯刚度。随后,许多学者针对志波模型的不足之处进行了修正,考虑了更多的影响因素。如: 廖少明[2]提出了环缝影响范围的概念,修正了志波由纪夫的理论,使计算出的环缝抗弯刚度更加贴近实际; 徐凌[3]在计算环缝抗弯刚度的过程中考虑了环缝断面上压力的影响,能够更加合理地贴近管片环的真实边界条件; 鲁志鹏[4]、周宁等[5]综合考虑了螺栓预应力和环缝影响范围对环缝抗弯刚度的影响; 张文杰等[6]考虑了横向刚度和环缝影响范围对环缝抗弯刚度的影响; 叶飞等[7]考虑了横向刚度和横向变形对环缝抗弯刚度的影响。解析解的优势是概念清晰,且当计算参数发生变化时能够很快得到解答。现有研究主要关注环缝的抗弯性能,对环缝的抗剪性能研究相对比较缺乏。而实际上,环缝错台是工程中的常见现象。在错台条件下,环缝以抗剪为主,环缝断面上的弯矩很小。因此,有必要进一步发展求解环缝抗剪性能的解析方法。
部分学者采用足尺试验的方法对环缝受力性能展开研究。如: 闫治国等[8]以青草沙输水隧道为研究对象,进行了一系列足尺试验,其研究结果表明,环缝的剪切破坏过程分为3个阶段; 朱瑶宏等[9]基于宁波轨道交通隧道进行了一系列足尺试验,获取了不同纵向压力下环缝的抗剪刚度; 李冬梅等[10]基于上海长江隧道进行了足尺试验,并依据试验结果归纳出了一系列公式,用于计算不同错台条件下环缝的抗剪刚度; J. Buco等[11]通过足尺试验,对地下混凝土管道的拉弯剪复合作用进行了试验研究; T. Putke等[12]对环缝各受力构件(剪力销、凹凸榫)在环缝破坏过程中所起到的作用进行了足尺试验研究; A. Salemi等[13]通过足尺试验对环缝抗剪刚度与环缝断面纵向压力的关系进行了研究。足尺试验中管片的边界条件最接近于实际工程,其结果具有较高的准确性。但是,现有研究其结果主要来自对试验数据的归纳,而很少基于力学原理对环缝的破坏机制进行解析。
综上所述,现有关于环缝受力性能的理论研究,主要关注抗弯机制,很少涉及到抗剪机制,且现有的足尺试验研究与理论研究之间缺乏联系。为改进现有研究的不足,本研究以某斜螺栓连接大直径盾构隧道环缝为研究对象,首先设置1组足尺试验,揭示其破坏机制; 随后采用计算力学的方法,将其破坏机制推广到构造相似的其他斜螺栓连接环缝; 最后通过敏感性分析,揭示各因素对斜螺栓连接环缝抗剪刚度的影响。
1 斜螺栓连接环缝剪切破坏足尺试验
1.1 研究对象与试验构件
以某大直径越江隧道环缝为研究对象,进行足尺试验。该隧道外径为11 800 mm,内径为10 800 mm,环宽为2 m,壁厚为500 mm,环缝由46根M30斜螺栓连接。环缝的细部构造如图1所示。斜螺栓总长度为588 mm,其中与套筒连接的螺牙段长度为160 mm,螺杆光滑段长度为428 mm。斜螺栓与水平方向的夹角为30°。
本次试验的构件由3块管片构成。剪切块1和剪切块3的长度为350 mm,剪切块2的长度为2 700 mm,3块管片的高度均为500 mm。环缝尺寸与原隧道完全相同。试验构件如图2所示。
1.2 加载设备与测试方案
本次试验所采用的加载设备如图3(a)所示,在加载设备作用下试验构件的受力简图如图3(b)所示。本次试验施加2个方向的荷载。其中竖向荷载2F由竖向千斤顶通过2根分配梁施加到试验构件上,该荷载模拟的是环缝剪力。水平荷载FN通过水平向千斤顶通过辅助钢构件施加到试验构件上,该荷载模拟的是环缝断面上作用的纵向压力。由构件的受力简图可知,环缝剪力等于竖向荷载的1/2,大小为F。
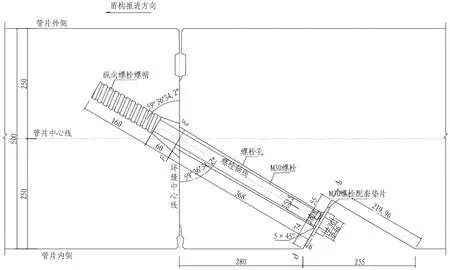
图1 某越江隧道环缝构造 (单位: mm)
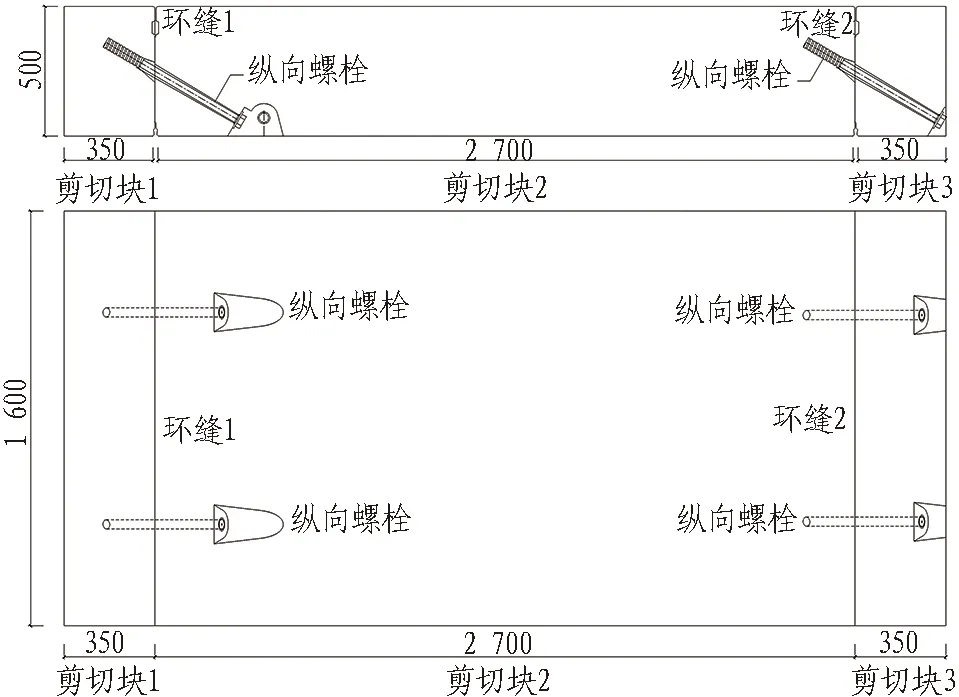
图2 试验构件(单位: mm)

(a) 加载设备

(b) 受力简图
本次试验在2条环缝上共布置12个位移计,用于测量环缝错台。测点布置如图4所示。
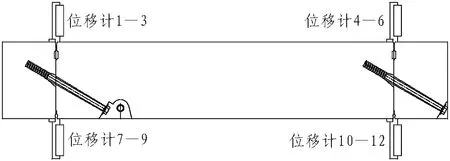
图4 测点布置
1.3 试验工况及加载方案
本次试验设置的工况为模拟隧道掘进过程中环间产生错台时管片环的受力状态。假定隧道掘进过程中盾构的顶推力在环面上均匀分布,则依据施工过程中实测的盾构顶推力,算得试验构件1.6 m宽度上分配到的压力约为500 kN。在加载过程中,首先将水平荷载FN加载至500 kN,随后维持水平荷载FN不变,逐级施加垂向荷载F,每级10 kN,直至试验构件发生破坏。
1.4 试验现象
试验后,拆解试验构件,观察到环缝斜螺栓如图5所示。

图5 试验后的环缝斜螺栓
由图5可知: 环缝斜螺栓在加载过程中出现了2个明显的塑性铰区,其中塑性铰1位于螺牙段和螺杆光滑段的交界点,塑性铰2位于环缝接触面附近。
1.5 试验结果
本次试验实测的环缝错台-环缝剪力关系如图6所示。

图6 环缝错台-环缝剪力关系
由图6可知,不论环缝1还是环缝2,其破坏过程均分为3个阶段: 第1阶段环缝抗剪刚度近乎无穷大,第2阶段环缝抗剪刚度几乎为0,第3阶段环缝抗剪刚度随错台发展不断变化。
2 环缝破坏全过程解析
2.1 研究对象
第1节中所述环缝剪切足尺试验展示了某一具体隧道的环缝剪切破坏过程,本节将通过解析解法对上述破坏过程的机制进行分析,并将其推广到结构类似的其他斜螺栓连接盾构隧道环缝。
典型斜螺栓及螺栓孔构造如图7所示。其中C为管片2螺栓孔下边缘与环缝的交点,B为管片1螺栓孔上边缘与环缝的交点。为便于描述,以斜螺栓光滑段和螺牙段的交点O为原点,沿斜螺栓轴向布置X轴,垂直螺栓轴向布置Y轴,建立平面直角坐标系。

图7 典型斜螺栓及螺栓孔构造
2.2 环缝破坏过程分析
由图6可知,环缝1与环缝2的破坏过程截然不同。其原因在于,对于图7所示构造的斜螺栓连接环缝,斜螺栓一端咬合于套筒中(以下称为锚固端),一端穿过手孔(以下称为活动端)。锚固端相对于活动端向上错动或是向下错动,斜螺栓的破坏机制不同,环缝的受力性能也不相同。
2.2.1 锚固端相对于活动端向下错动环缝破坏过程
锚固端相对于活动端向下错动时,环缝的破坏过程如图8所示。图中f表示环缝接触面上作用的摩擦力。假定管片1相对于管片2向下错动,管片2施加在管片1上的摩擦力方向向上,管片1施加在管片2上的摩擦力方向向下。
由图8可知: 1)当相邻2环管片由于某种原因产生相对运动趋势时,环缝断面上的静摩擦力首先发挥作用。在环缝剪力不超过最大静摩擦力时,环缝错台不会发展。将此阶段定义为环缝破坏过程的第1阶段。2)当环缝剪力略大于环缝最大静摩擦力时,由于螺栓孔和螺栓之间存在间隙,在环缝剪力不增加的情况下环缝错台将产生数mm的发展。将此阶段定义为环缝破坏过程的第2阶段。3)当斜螺栓与螺栓孔产生第1个接触点时,环缝剪力的增量将由斜螺栓单独承担。随着环缝错台的逐渐增大,斜螺栓与螺栓孔之间的接触点将逐渐增加,斜螺栓将依次产生2个塑性铰,环缝因此丧失承载能力而破坏。将此阶段定义为环缝破坏过程的第3阶段。
应该指出,由于管片1相对于管片2向下错动,所以在第3阶段斜螺栓断面上不会产生任何轴力,斜螺栓以受弯为主。在不同错台条件下,斜螺栓的支撑条件不同,斜螺栓的抗弯刚度亦有所不同,因此导致环缝抗剪刚度发生变化。
2.2.2 锚固端相对于活动端向上错动环缝破坏过程
当锚固端相对于活动端向上错动时,环缝的破坏过程如图9所示。
由图9可知: 锚固端相对于活动端向上错动时,环缝破坏过程的第1阶段、第2阶段与锚固端相对于活动端向下错动时完全相同;但是在第3阶段,由于螺母与螺栓孔端面之间会产生较大的挤压力N,导致斜螺栓全断面受到大小为N的拉力,在斜螺栓与螺栓孔的第2个接触点产生之前,斜螺栓就会拉坏; 整个第3阶段斜螺栓以受拉为主,刚度不变,因此整个第3阶段环缝的抗剪刚度也不发生变化;这是与锚固端相对于活动端向下错动的情形截然不同的。
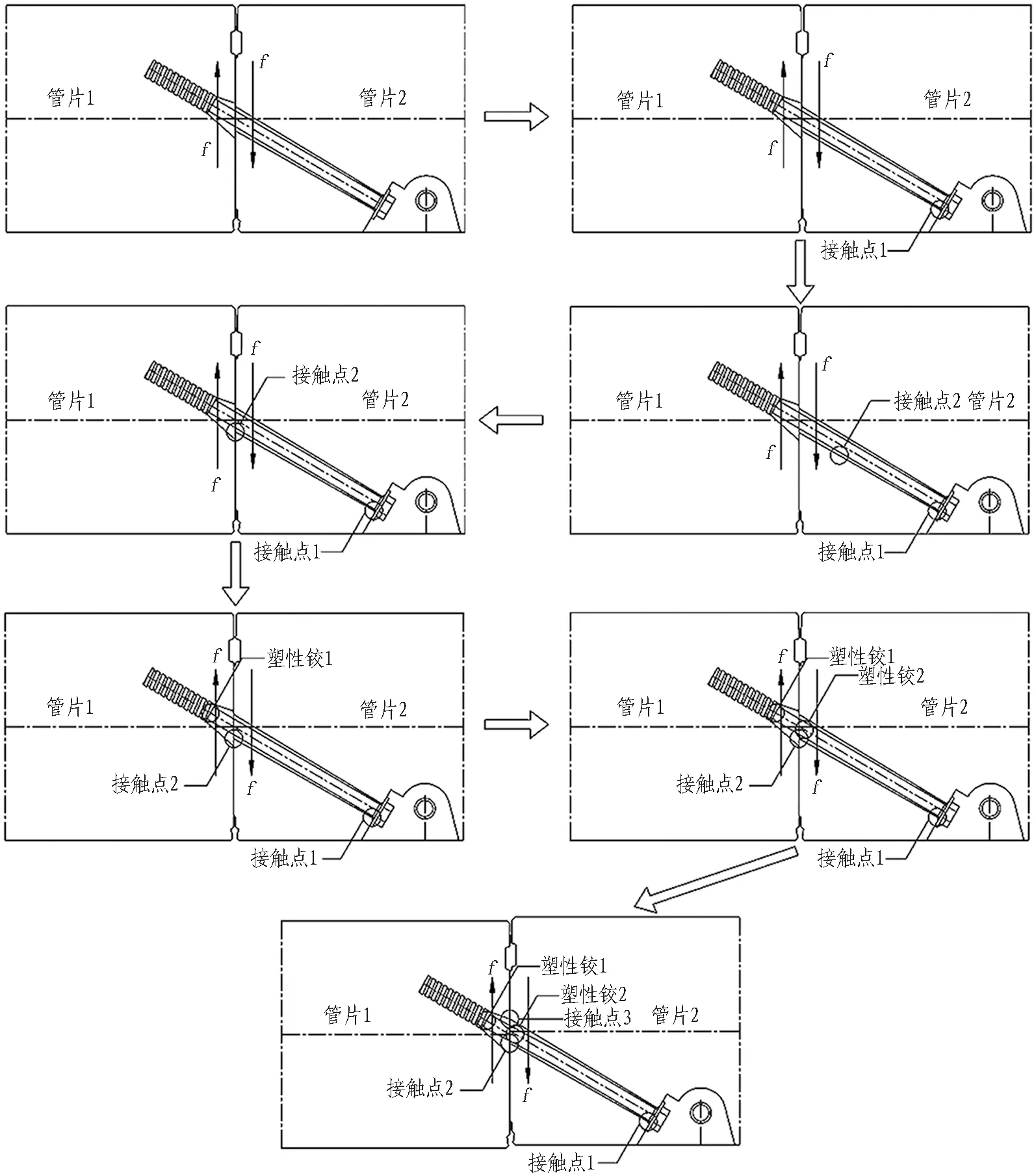
图8 锚固端相对向下错动环缝破坏过程示意图

图9 锚固端相对向上错动环缝破坏过程示意图
2.3 斜螺栓破坏过程详解
环缝破坏的第1阶段和第2阶段其受力状态都是比较清晰的;但在第3阶段,由于斜螺栓的受力状态十分复杂,且随错台的发展不断变化,有必要对其进行详细分析。以下为便于描述,将第3阶段的第1阶段记为环缝破坏过程阶段3.1,将第3阶段的第2阶段记为环缝破坏过程阶段3.2,依此类推。
2.3.1 锚固端相对活动端向下错动斜螺栓受力分析
2.3.1.1 线弹性阶段斜螺栓受力分析
由于螺牙与套筒咬合良好,螺牙和光滑螺杆的交界点可以被视为固定端约束。在环缝破坏第2阶段,斜螺栓已经与螺栓孔在螺母附近产生了接触点1,接触点1也可被视为固定支座。斜螺栓受力变形进入第3.1阶段,其受力简图和弯矩图如图10所示。
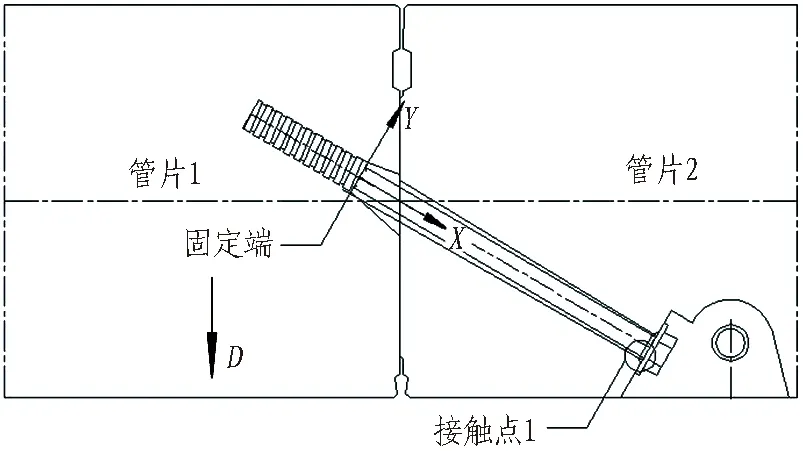
(a) 第3.1阶段边界条件

(b) 第3.1阶段受力简图

(c) 第3.1阶段弯矩图
由结构力学的基本原理可知,第3.1阶段的弯矩M的表达式如式(1)所示。
(1)
D′=Dcosθ。
(2)
式(1)—(2)中:EI为螺栓的截面抗弯刚度;θ为斜螺栓与水平方向的夹角;l为螺母端到螺牙和螺杆光滑段的交界点的距离;D为环缝破坏第3阶段新产生的环缝错台;D′为D在Y方向的分量。
依据材料力学基本原理,弯矩是挠度的二阶导数,结合阶段1斜螺栓两端固定的边界条件,可以求得斜螺栓的挠度
(3)
螺栓孔的边缘是一条直线,令该直线在坐标系中的表达式为
(4)
式中: -b/l为该直线的斜率;t为该直线在Y轴上的截距。
令螺栓变形过程中螺栓孔边缘与斜螺栓边缘的距离
ΔY=Y1-Y2。
(5)
对ΔY求导,可得
(6)
令ΔY′=0,求得ΔY的极小值点为X=l0。可知,在斜螺栓受力变形的过程中,X=l0处螺栓距离螺栓孔最近,随着环缝错台D的不断增加,该点是整条斜螺栓上首先接触到螺栓孔的点。令ΔY(l0)=0,解得D′=D1cosθ。此时在X=l0处螺栓已经与螺栓孔相接触。相当于在螺杆中部产生了一个新的支点接触点2,接触点2与固定端之间的距离为l0。斜螺栓受力变形进入第3.2阶段,其受力简图和弯矩图如图11所示。
值得指出的是,至此整根螺杆尚处于线弹性状态,可以采用结构力学中的叠加法思想,先独立计算每一阶段的内力和变形,然后再依据需要进行叠加。由结构力学的基本原理可知,不计第3.1阶段产生的变形,第3.2阶段螺杆的变形如图11所示。可知: 第3.2阶段的变形,使得支点左侧螺杆产生向下的位移及支点右侧螺杆产生向上的位移。可以预见,支点随着环缝错台的发展将会逐渐向左移动。当支点运动到环缝处时,由于左侧螺栓孔的直径显著大于右侧螺栓孔,这一运动过程结束。运动过程结束时,支点位于环缝断面附近,将此状态视为螺栓受力变形第3.2阶段的终点。假定第3.2阶段结束时,第3.2阶段产生的环缝错台增量为D2。

(a) 第3.2阶段边界条件

(b) 第3.2阶段受力简图
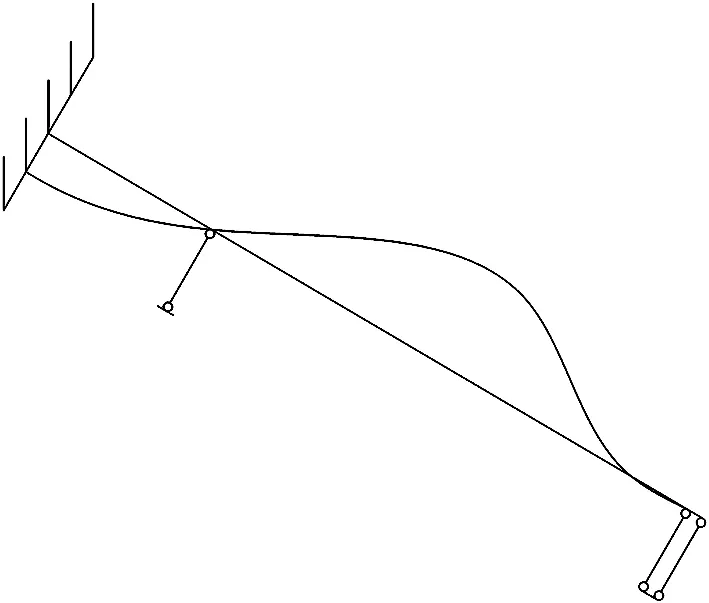
(c) 第3.2阶段变形图
可以预见,由于斜螺栓的跨中支点在整个第3.2阶段其位置不断左移,因此整个第3.2阶段环缝的抗剪刚度也在不断增大。如图12所示,设环缝断面与斜螺栓轴线的交点和锚固端之间的距离为l′,则第3.2阶段初始环缝抗剪刚度K20和第3.2阶段最终环缝抗剪刚度K21如式(7)—(8)所示。
(7)
(8)
当斜螺栓的跨中支点移动到环缝与斜螺栓的交界点时,斜螺栓的受力变形进入第3.3阶段,其受力简图和弯矩图如图12所示。

(a) 第3.3阶段边界条件

(b) 第3.3阶段受力简图

(c) 第3.3阶段弯矩图
2.3.1.2 塑性铰产生后的斜螺栓受力分析
在斜螺栓受力变形的第3.1、3.2、3.3阶段,由于斜螺栓和螺栓孔之间的间距较小,斜螺栓处于线弹性状态。但是,随着环缝错台的进一步发展,斜螺栓上某些位置将产生塑性铰。美国AISC-LRFD规范[14]认为,当截面的内力满足式(9)—(10)要求时可以认为该截面位置已经形成了塑性铰。
(9)
(10)
式(9)—(10)中:p为螺栓截面上的轴力;M为螺栓截面上的弯矩;py为截面的极限轴力;Mp为截面的塑性弯矩。
对于本研究而言,第3.1、3.2、3.3阶段断面上基本没有轴力,横截面塑性强度就是截面塑性极限弯矩Mp。
由第3.1、3.2、3.3阶段的弯矩图可知,3个阶段弯矩叠加的结果是X=0处弯矩最大,此处为第1个塑性铰出现的位置。假定第1个塑性铰出现时环缝第3.3阶段的错台达到D3,则由结构力学的基本原理可知,D3可通过式(11)求解。
D2cosθ=Mp。
(11)
此处将第3.2阶段的刚度取为第3.2阶段结束时刚度和第3.2阶段初始时刚度的平均值。
当X=0处形成塑性铰后,斜螺栓的受力简图再次发生变化,斜螺栓的受力变形进入第3.4阶段,其受力简图和弯矩图如图13所示。

(a) 第3.4阶段边界条件
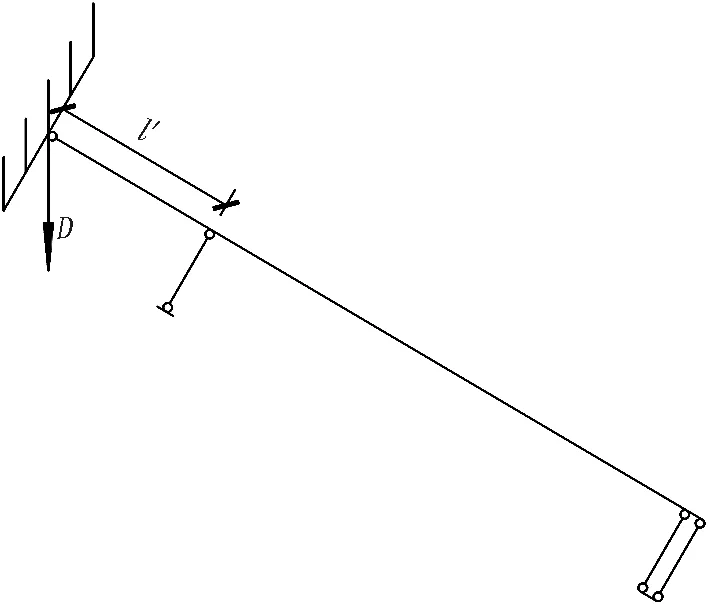
(b) 第3.4阶段受力简图

(c) 第3.4阶段弯矩图
由于塑性铰本身的受力特性不同于理想铰,其不能够自由转动,塑性铰产生后第3.1、3.2、3.3阶段产生的内力仍然存在于螺杆各截面,此时螺杆截面的内力等于第3.4阶段新增的内力与第3.1、3.2、3.3阶段内力之和。
由第3.4阶段的弯矩图可知,斜螺栓跨中支点处(X=l′)的弯矩最大。由于第3.1、3.2、3.3阶段X=0附近的弯矩远大于其余位置弯矩,第1个塑性铰形成时距离该塑性铰较远的斜螺栓横截面上只具有较小的弯矩。第2个塑性铰出现的主要原因是第3.4阶段的新增弯矩,而非第3.1、3.2、3.3阶段的弯矩累积。综上所述,第2个塑性铰将出现在斜螺栓跨中接触点2附近。设第2个塑性铰出现时第3.4阶段的环缝错台为D4,则D4应满足式(12)的要求。

(12)
此处将第2阶段的刚度取为第3.2阶段结束时的刚度K21,会造成计算出的内力值较实际内力偏大,这是一种偏于保守的做法。主要是考虑到此时斜螺栓上已经形成了2个塑性铰,处于十分不稳定的状态。
第2个塑性铰出现时,斜螺栓的受力变形进入了第3.5阶段,此时斜螺栓的受力简图如图14所示。可知,由于第3.5阶段整条斜螺栓上已经形成了2个塑性铰,斜螺栓不再具有抵抗环缝错台的能力,斜螺栓将发生大变形。在这一变形过程中,虽然环缝错台很大,但是由于斜螺栓此时抵抗环缝错台的刚度丧失,在斜螺栓任意截面上不会有新的弯矩产生。但另一方面,由于斜螺栓产生大变形,因为此变形而产生的螺杆伸长量无法忽略,故而会在断面上形成较大的轴力。假定某处于第3.5阶段的斜螺栓,其连接的环缝在第3阶段的总错台为D,则螺杆的轴力如图14所示,螺杆上作用的轴力可按照式(13)计算。
(13)
式中:N为螺栓轴力;EA为斜螺栓的抗拉刚度。
抗拉强度较低的斜螺栓将在轴力N的作用下发生断裂。对于在轴力N作用下不会断裂的高强螺栓,大变形最终的结果为图7所示左侧螺栓孔上边缘B点向下错动后与螺杆接触,形成新的支点。支点C和支点B之间很短的一段螺杆处于近乎纯剪的受力状态,最终斜螺栓在切应力和正应力的共同作用下发生破坏。此过程可以视为斜螺栓受力变形的第3.6阶段。

(a) 第3.5阶段边界条件

(b) 第3.5阶段受力简图

(c) 第3.5阶段弯矩图
2.3.2 锚固端相对活动端向上错动斜螺栓受力分析
当锚固端相对于活动端向上错动时,除弯矩外,斜螺栓各断面还将产生附加轴力。计算结果表明,微小的错台即可引起很大的附加轴力。通常,在第2个接触点产生之前,斜螺栓就已经屈服。因此,锚固端相对于活动端向上错动的环缝,其破坏过程的第3阶段环缝抗剪刚度不变。第3阶段新增的斜螺栓轴力ΔN与第3阶段新增错台D的关系如式(14)所示。锚固端相对于活动端向上错动时斜螺栓环缝抗剪刚度K′在第3阶段中的取值可按照 式(15)计算。
(14)
(15)
2.4 环缝破坏过程小结
综合以上分析,理论上环缝破坏过程各阶段抗剪刚度如表1所示。其中,K表示单根斜螺栓连接的环缝锚固端相对于活动端向下错动的环缝刚度,K′表示单根斜螺栓连接的环缝锚固端相对于活动端向上错动的环缝刚度。除刚度外,还需给出环缝破坏的判定依据。工程界普遍认为,当结构受到的荷载几乎没有增长,而变形持续发展时,可判定结构发生了破坏。具体到盾构隧道环缝,当环缝剪力几乎没有增长而环缝错台不断发展时,判定环缝破坏。不难看出,依据此标准,对于锚固端相对于活动端向上错动的环缝,斜螺栓受拉屈服时可以判定环缝发生破坏。对于锚固端相对于活动端向下错动的环缝,当斜螺栓上出现第2个塑性铰时可以判定环缝发生破坏。

表1 环缝抗剪刚度表
2.5 试验结果与解析解的对比分析
2.5.1 环缝刚度解析结果
对照第1.5节中的试验结果,其与解析解在定性上是相符的。本节定量分析解析解与试验结果之间的异同及其原因,以进一步验证解析解的准确性。由图2可知,环缝1锚固端相对于活动端向上错动,环缝2锚固端相对于活动端向下错动。将图1所示环缝的细部尺寸带入第2节所述各公式中,解得环缝2刚度变化规律如表2所示,环缝1刚度变化规律如表3所示。其中,D总表示环缝第1、2、3阶段的总错台。F表示环缝剪力。由图1可知: 1)试验构件的环缝由2根斜螺栓连接,进入第3阶段后,环缝2的实际抗剪刚度为2K; 2)试验构件的环缝由2根斜螺栓连接,进入第3阶段后环缝1的实际抗剪刚度为2K′。

表2 环缝2刚度变化表
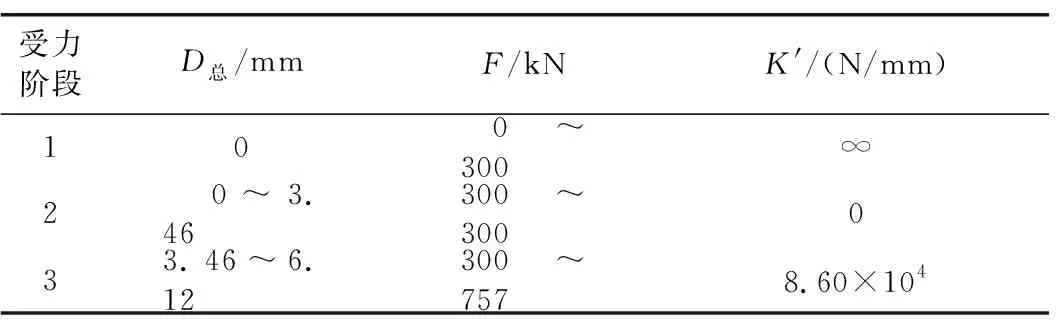
表3 环缝1刚度变化表
2.5.2 环缝2解析解与试验结果比较
在同一个坐标系中描述环缝2理论环缝剪力-环缝错台关系与实测环缝剪力-环缝错台关系,如图15所示。

图15 环缝2错台实测值与理论值关系图
由图15可知: 于环缝2而言,实测环缝错台-环缝剪力曲线和理论环缝错台-环缝剪力曲线具有相同的变化趋势。具体分析如下:
1)当环缝剪力为0~300 kN时(阶段1),环缝剪力主要由摩擦力承担,环缝错台几乎没有发展,不论对理论值还是实测值均是如此。
2)当环缝剪力为300 kN时(阶段2),理论环缝错台-环缝剪力曲线出现水平段,这主要是由于斜螺栓活动端与螺栓孔之间存在3 mm的空隙。在此阶段,实际环缝错台-环缝剪力曲线斜率很小,近乎水平。这表明在阶段2理论环缝错台-环缝剪力曲线与实测环缝错台-环缝剪力曲线具有一致性。本阶段实测环缝剪力-环缝错台曲线之所以具有很小的斜率,主要是由于螺母与螺栓孔端面具有一定大小的摩擦力,如图16所示。理论模型中未考虑此影响因素。
3)当环缝剪力为300~311.24 kN时(阶段3.1),实测环缝剪力-环缝错台曲线与理论环缝剪力-环缝错台曲线具有相同的斜率,但此阶段在相同环缝剪力作用下,理论值的错台均要比实测值稍大。这主要是由于,每一级荷载作用下的理论错台等于试验中该级荷载作用下试验构件错台发展完全稳定后的错台值。而在试验过程中,由于目前没有相关标准判断环缝错台何时达到完全稳定,常采用的做法是当环缝错台发展速度很缓慢时开始施加下一级荷载。每级荷载造成的误差会在环缝错台-环缝剪力曲线上累积,从而造成多个加载步以后,理论错台较实测错台稍有偏大的情况。
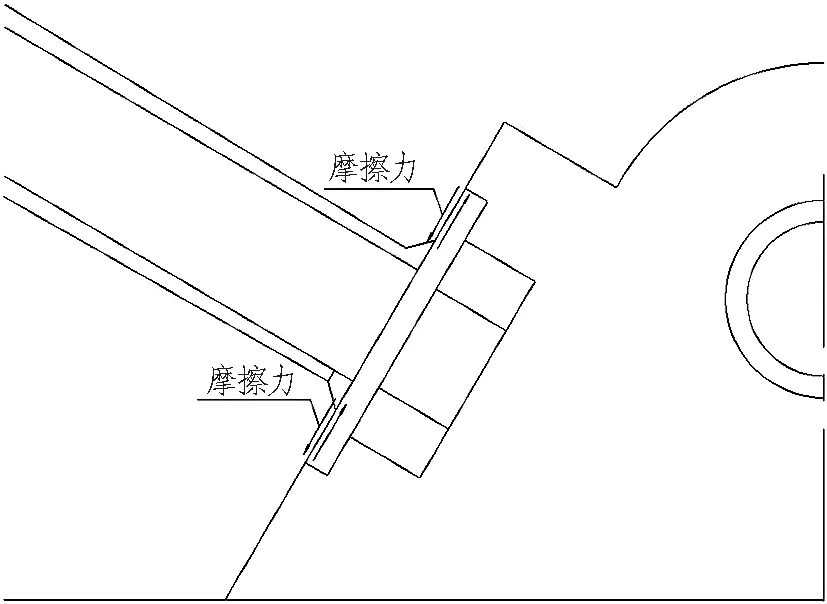
图16 螺母与螺栓孔端面摩擦力
4)当环缝剪力为311.24~341.36 kN时(阶段3.2),理论环缝错台-环缝剪力曲线与实测环缝错台-环缝剪力曲线具有良好的一致性。
5)当环缝剪力为341~375 kN时(阶段3.3),实测环缝错台-环缝剪力曲线斜率小于理论环缝错台-环缝剪力曲线,这表明实测环缝刚度小于理论环缝刚度。这种现象产生的原因,主要是理论推导的过程中假定螺栓孔钢筋混凝土完全不会破坏,而试验过程中螺栓孔附近钢筋混凝土虽然不会先于斜螺栓丧失承载能力,却不免会产生一定的局部破坏,从而造成斜螺栓的活动空间增大,并由此导致环缝错台大于理论值、环缝刚度小于理论值的后果。螺栓孔位置发生的混凝土局部破坏如图17所示。

图17 螺栓孔附近局部破坏
6)当环缝剪力为375~481 kN时(阶段3.4),实测环缝刚度比理论环缝刚度稍小。其原因同样是螺栓孔附近混凝土发生局部破坏。值得指出的是,在环缝剪力达到425 kN时,实测环缝错台-环缝剪力曲线进入了一段较短的平台段。主要是由于斜螺栓跨中支点位置的混凝土发生了局部破坏,造成斜螺栓在无支撑的条件下快速向下错动,直至接触到未破坏的混凝土或螺旋筋,才恢复抗剪刚度。理论求得右侧环缝的抗剪承载力为481 kN,实测右侧环缝抗剪承载力为500 kN,二者相差4%,具有良好的一致性。
2.5.3 环缝1解析解与试验结果比较
在同一个坐标系中描述环缝1理论和实测环缝剪力-环缝错台曲线,结果如图18所示。具体分析如下:
1)环缝剪力为0~300 kN时(阶段1),理论上环缝错台没有发展,环缝刚度为无穷大。实测环缝错台几乎没有发展,实测环缝刚度接近无穷大。极小的(约0.6 mm)的环缝错台是由于实际摩擦力与理想化的静摩擦力有一定的区别。二者具有良好的匹配性。
2)当环缝剪力为300 kN时(阶段2),理论环缝刚度为0,实测值表明环缝此时尚具有较小的刚度,这主要是由于螺母垫片和螺栓孔端面的摩擦力。这种趋势相比于右侧环缝更加明显,这是由于左侧环缝属于锚固端向上错动的环缝,其螺母垫片与螺栓孔端面之间的正压力更大,从而造成其间摩擦力更大。
3)当环缝剪力大于300 kN时(阶段3),环缝理论刚度稍大于环缝实测刚度,这可能是由于螺栓孔附近混凝土的局部破坏。
由于本次试验所采用的试验构件的构造特殊,当环缝2发生破坏后将无法继续进行加载,此时环缝1远远未达到其承载能力极限状态,无法比较环缝1的理论强度和实测强度。
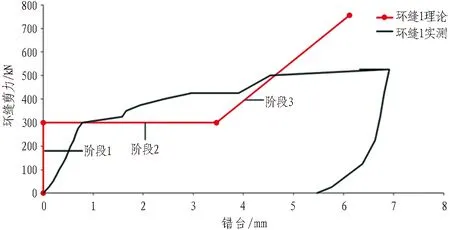
图18 环缝1错台实测值与理论值关系图
3 环缝刚度影响因素敏感性分析
由以上分析可知,盾构隧道环缝刚度的影响因素众多,但是各因素对环缝刚度的影响大小不同。为找出对环缝刚度影响最大的因素,并在设计过程中对其加以控制,有必要对环缝刚度的各个影响因素进行敏感性分析。
绝大多数隧道环缝的错台较小,因此环缝的初期抗剪刚度最为重要。而由于第1阶段抗剪刚度和第2阶段抗剪刚度不受任何设计参数的影响,所以将第3.1阶段抗剪刚度作为敏感性分析系统的输出变量。由表1可知,第3.1阶段环缝刚度受到斜螺栓倾斜角度、螺栓直径、螺栓长度3个因素的影响,将此3因素视为系统的输入变量。此处,将敏感性系数取为系统输出变量对系统输入变量的一阶偏导数[15-16]。
由于各输入变量单位和取值范围均有不同,故首先对其进行归一化处理。假定某一因素的变化范围为(Xmin,Xmax),则对该因素的某一取值X进行归一化后的取值如式(16)所示。
(16)
经过归一化后,输入变量的取值范围将统一变为(0,1)。
以下分析所采用的参数与第2节试验中参数相同。
3.1 锚固端相对向上错动环缝刚度影响因素分析
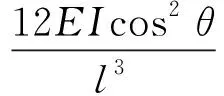
(17)
由式(17)可知: 对于锚固端相对向上错动的环缝,环缝第3.1阶段抗剪刚度随斜螺栓与水平方向夹角的增加而增加,随斜螺栓长度的增加而减小,随斜螺栓直径的增加而增加。其中,斜螺栓倾角对环缝刚度的影响大于斜螺栓直径,斜螺栓直径对环缝刚度的影响大于斜螺栓长度。
3.2 锚固端相对向下错动环缝刚度影响因素分析

(18)
由式(18)可知: 对于锚固端相对向下错动的环缝,第3.1阶段的抗剪刚度随斜螺栓与水平方向夹角的增加而减小,随斜螺栓长度的增加而减小,随斜螺栓直径的增加而增加。其中对环缝抗剪刚度影响最大的是斜螺栓倾角,其次是斜螺栓长度,对环缝抗剪刚度影响最小的是斜螺栓直径。
4 结论与建议
1)对于斜螺栓连接的无凹凸榫环缝,其剪切破坏过程分为3个阶段,第1阶段环间剪力由静摩擦力平衡,环缝抗剪刚度无穷大; 第2阶段在环缝剪力几乎不增加的情况下错台有所发展,环缝抗剪刚度为0,主要是由于斜螺栓与螺栓孔之间的间隙; 第3阶段环缝剪力增量由斜螺栓承担,环缝抗剪刚度随斜螺栓支撑条件以及塑性铰产生过程而变化。
2)相邻2环管片的相对运动方向会对第3阶段环缝受力性能产生很大影响。螺栓锚固端所在管片环相对向上错动时,第3阶段环缝抗剪刚度基本不变,在破坏前一直维持在较高水平。螺栓锚固端所在管片环相对向下错动时,第3阶段抗剪刚度经历了先增加、后减小、再增加的复杂变化过程。相比较而言,锚固端向上错动的环缝具有更大的抗剪刚度,锚固端向下错动的环缝具有较好的变形能力。
3)螺栓锚固端所在管片环相对向上错动时,斜螺栓以受拉为主,环缝最终破坏原因是斜螺栓受拉屈服; 螺栓锚固端所在管片环相对向下错动时,斜螺栓以受弯为主,环缝最终破坏原因是斜螺栓上产生2个塑性铰从而丧失抗弯刚度。
4)对于锚固端相对向上错动的环缝,环缝刚度最主要的影响因素是斜螺栓与水平方向的夹角,其次是斜螺栓直径,再次是斜螺栓长度。对于锚固端相对向下错动的环缝,环缝刚度最主要的影响因素是斜螺栓与水平方向的夹角,其次是斜螺栓长度,再次是斜螺栓直径。
通过对以上结论的分析,建议在设计中通过调整斜螺栓与水平方向的夹角,以获取所需的环缝刚度。

