圆中空钢管混凝土叠合构件纯弯性能研究
任庆新,魏秋宇,丁纪楠
(沈阳建筑大学土木工程学院,辽宁 沈阳 110168)
中空钢管混凝土叠合构件是由钢筋混凝土包裹在空心钢管外而成的新型结构形式[1-3]。相比于钢筋混凝土构件,中空钢管混凝土叠合构件由于中心被空心钢管取代,从而具有截面易开展、抗弯刚度大、自重轻等优点,适用于桥梁结构中的桥墩、高层建筑中的大直径柱、各种支架柱以及送变电杆塔等结构,具有广泛应用前景。
A.Abouzied[4]研究了矩形中空GFRP混凝土叠合构件纯弯性能;Q.Giuseppe[5]对圆中空钢筋混凝土构件压-弯作用下的承载力进行了计算及简化;梁荟[6]研究了方中空钢管混凝土叠合构件纯弯性能,J.Y.Chen[7]研究了箱型中空钢管混凝土叠合构件的纯弯性能;刘清等[8]对圆中空夹层钢管自密实混凝土抗弯性能进行了试验研究。
目前对中空钢管混凝土叠合构件的研究尚处于起步阶段。基于此,笔者建立了圆中空钢管混凝土叠合构件纯弯有限元模型,并在试验验证基础上,利用有限元软件ABAQUS对典型算例受力全过程工作机理以及不同参数对承载力的影响进行分析,研究内钢管直径与混凝土强度对试件受力性能的影响,并以叠加理论和极限平衡理论为基础提出了构件在纯弯作用下的抗弯承载力简化计算公式。
1 有限元模型
1.1 模型参数
笔者以试件CB1建立有限元模型,构件长L=2 000 mm,截面直径D=200 mm;钢材选用Q345B,钢材屈服强度fys=378 MPa,钢管外径d=80 mm,钢管壁厚t=2.76 mm;纵筋采用Φ12 HRB400螺纹钢筋,纵筋屈服强度fyz=384 MPa,箍筋为Φ6.5 HPB300光圆钢筋,箍筋屈服强度fyg=326 MPa;箍筋间距为100 mm;选用C40混凝土,混凝土立方体抗压强度fcu=45.2 MPa,保护层厚度25 mm。试件设计如图1所示,试件参数见表1。

图1 试件截面Fig.1 Cross-section of specimens

表1 试件参数Table 1 Parameters of specimens
1.2 材料本构关系
混凝土本构关系分为无约束混凝土和箍筋约束混凝土两部分,无约束部分选用过镇海[9]提出的无约束混凝土本构模型,箍筋约束部分采用L.H.Han[10]提出的应力-应变关系模型,钢筋本构关系采用双折线应力-应变关系,钢管的本构关系采用五段式[11]本构模型。
1.3 模型建立
1.3.1 单元类型选取
钢管采用四节点减缩积分格式的壳单元(S4R)来模拟,在壳单元厚度上采用九个积分点的Simpson积分。纵筋和箍筋采用二节点三维线性桁架单元(T3D2),组合成钢筋骨架内嵌于混凝土中。混凝土采用八节点六面体线性减缩积三维实体单元(C3D8R)。有限元模型见图2。

图2 有限元模型Fig.2 Finite element analysis model
1.3.2 边界条件、界面接触及加载方式
为简化模型的建立,加载及支座位置设置刚性垫块,左侧垫块模拟固定铰支座,限制X、Y、Z方向的位移,右侧垫块模拟滚动铰支座,限制X、Y方向的位移。通过设置参考点Y方向的位移进行位移加载[12]。钢管与端板之间采用壳固耦合的接触方式。混凝土与端板、刚性垫块之间采用tie约束。混凝土与钢管之间:法线方向采用“硬”接触,切线方向的粘结滑移采用“罚”函数,摩擦系数取0.6[13]。
1.4 试验验证
笔者对试验构件CB1、CB2和CB3建立力学模型,并用试验结果验证。3个试件破坏模态见图3,不同参数下弯矩-挠度(M-um)曲线见图4,承载力对比如图5所示。由图3可知,模拟结果与试验结果吻合较好。由图4可知,有限元模拟得到的M-um曲线与试验实测结果基本一致,且初始阶段刚度大致相等,验证了有限元模型的准确性。由图5得到弯矩试验值与有限元模拟值的比值平均值为0.939,标准差为0.042,上述对比结果服从正态规律分布,Mue/MuFEM达到置信水平95%时的置信区间为(0.895,0.982)。

图3 试件破坏模态Fig.3 Failure modes of specimens
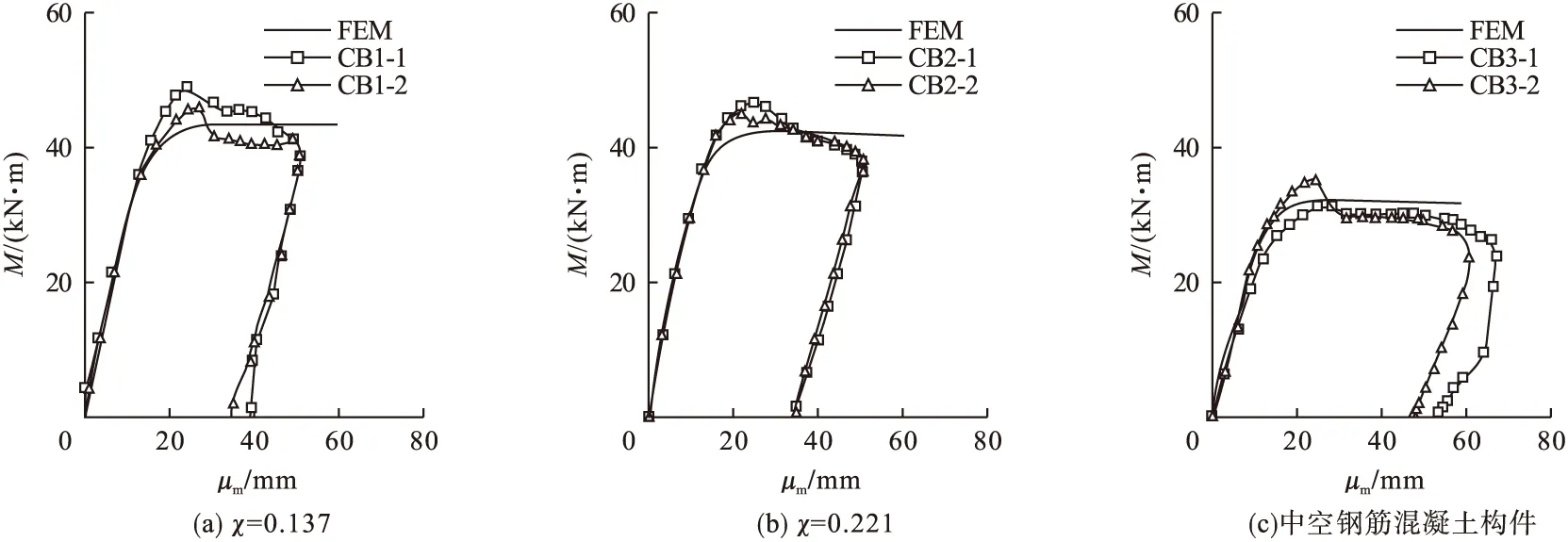
图4 M-um曲线Fig.4 Curves of M-um

图5 承载力对比Fig.5 Comparison between FEM and test results
2 工作机理分析
笔者将试件CB1作为典型算例进行分析纯弯工作机理。CB1的弯矩-挠度曲线特征点如图6所示,定义4个特征点。A点:受拉区混凝土发生塑性变形至开裂; B点:受拉区纵筋出现屈服;C点:试件达到峰值弯矩即抗弯承载力;D点:弯矩值下降到极限弯矩的85%。由此可以将圆中空钢管混凝土叠合构件受力全过程分为4个阶段:弹性阶段Ⅰ、弹性阶段Ⅱ、弹塑性阶段以及下降阶段。

图6 特征点示意图Fig.6 Schematic diagram of feature points
不同特征点处跨中混凝土应力分布如图7示,图中虚线为中性轴。A点为弹性阶段Ⅰ和弹性阶段Ⅱ分界点,混凝土受拉区边缘处拉应力增加至开裂应力,构件开始出现裂缝。B点为弹性阶段Ⅱ和弹塑性阶段分界点,此时构件混凝土已经出现多条明显裂缝,中性轴位置明显上移,构件的竖向变急速增大,达到极限拉应力的混凝土单元变多,受拉区面积不断增大,纵筋屈服进入塑性变形阶段。C点处,试件达到峰值弯矩,构件的竖向变形继续增加,混凝土中性轴继续上移,钢筋受拉区大部分达到屈服强度,钢管进入塑性变形阶段,受压侧混凝土被压碎。D点处,弯矩降降至峰值弯矩的85%,受压侧混凝土压碎区域增大,竖向挠度变化明显,受拉区混凝土裂缝达到2 mm左右。

图7 特征点跨中混凝土应力分布Fig.7 Stress distribution of middle span concrete
图8为构件跨中最低点处钢管与混凝土相互作用下应力-位移(P-um)曲线。从图中可以看出,构件处于弹性阶段时,钢管的泊松比大于混凝土,钢管与混凝土之间存在接触应力;随着加载的持续进行,受拉区混凝土进入塑性阶段,混凝土逐渐开裂,接触应力减小,钢管达到屈曲时钢管与混凝土脱离,接触应力先增大后减小。

图8 P-um曲线Fig.8 P-um curve of mid-section
3 参数分析
笔者分别选取钢管强度fys、钢管直径d、钢管厚度t、混凝土强度fcu、纵筋强度fyz和箍筋间距s共6个参数对构件承载力进行分析。不同参数对构件弯矩-挠度曲线(M-Δ)的影响见图9~图14。
3.1 钢管直径
不同钢管直径下构件弯矩-挠度曲线如图9所示。从图中可以得出,当钢管直径由80 mm增加至100 mm、120 mm时,弯矩由44.59 kN·m减小到43.42 kN·m、35.99 kN·m,分别减小了4.8%和19.3%。当钢管直径由80 mm增加到100 mm时,刚度由2.76 (kN·m)/mm减少至2.64(kN·m)/mm,减少了4.3%,直径由80 mm增加到120 mm时,刚度从2.76(kN·m)/mm增加到2.85(kN·m)/mm,增加了3.2%。可见,钢管直径对承载力影响显著,对刚度影响不明显。
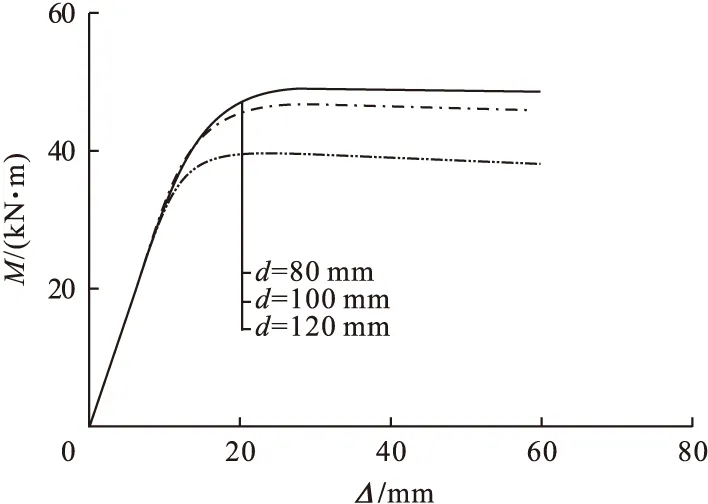
图9 不同钢管直径下弯矩-挠度曲线Fig.9 Influence of d on M-Δ curves
3.2 钢管厚度
不同钢管厚度下构件弯矩-挠度曲线如图10所示。从图中可以得出,当钢管厚度由3.0 mm减小到2.2 mm时,弯矩由44.59 kN·m减小到43.42 kN·m,减小了2.6 %;钢管厚度由3.0 mm增加到3.6 mm时,弯矩M由44.59 kN·m增加到45.25 kN·m,增大了1.5%。钢管厚度由3.0 mm减小到2.2 mm时,刚度由2.76(kN·m)/mm增加到2.79(kN·m)/mm,增加了1.1%;厚度由3.0 mm增加到3.6 mm时,刚度由2.76(kN·m)/mm增加到2.78(kN·m)/mm,增加了0.7%。可见,钢管厚度对承载力有较大影响,对刚度无明显影响。

图10 不同钢管厚度下弯矩-挠度曲线Fig.10 Influence of t on M-Δ curves
3.3 混凝土强度
不同混凝土强度下构件弯矩-挠度曲线如图11所示。从图中可以得出,混凝土强度由40 MPa增加至60 MPa、80 MPa时,弯矩由44.59 kN·m增加到47.57 kN·m、50.68 kN·m,分别增加了6.7 %和13.7%。当混凝土强度由40 MPa增加到60 MPa、80 MPa时,刚度由2.76(kN·m)/mm增加到2.87(kN·m)/mm、3.04(kN·m)/mm,分别增加了4.0%、10.1%。可见,混凝土强度对承载力及刚度影响显著。

图11 不同混凝土强度下弯矩-挠度曲线Fig.11 Influence of fcu on M-Δ curves
3.4 钢材强度
不同钢材强度下构件弯矩-挠度曲线如图12所示。从图中可以得出,当钢材强度由345 MPa增加到390 MPa、420 MPa时,弯矩由44.59 kN·m增加到44.89 kN·m、46.14 kN·m,分别减小了0.7%和3.5%。当钢材强度由345 MPa增加到390 MPa、420 MPa时,刚度由2.76 (kN·m)/mm增加到3.41(kN·m)/mm、3.42(kN·m)/mm,分别增加了23.6%、23.9%。可见,钢材强度对承载力影响不明显,对刚度影响显著。

图12 不同钢材强度下弯矩-挠度曲线Fig.12 Influence of fys on M-Δ curves
3.5 纵筋强度
不同钢管直径下构件弯矩-挠度曲线如图13所示。从图中可以得出,当纵筋强度由400 MPa减小到335 MPa时,弯矩由44.59 kN·m减小到43.86 kN·m,减小了1.6%;强度由400 MPa增加到500 MPa时,弯矩由44.59 kN·m增加到50.82 kN·m,增加了14%。当纵筋强度由400 MPa减小到335 MPa时,刚度由2.76(kN·m)/mm增加到3.48(kN·m)/mm,减少了26.1%;纵筋强度由400 MPa增加到500 MPa时,刚度由2.76(kN·m)/mm增加到3.67(kN·m)/mm,增加了33.0%。可见,纵筋强度对承载力响以及刚度影响显著。

图13 不同纵筋强度下弯矩-挠度曲线Fig.13 Influence of fyz on M-Δ curves
3.6 箍筋间距
不同箍筋间距下构件弯矩-挠度曲线如图14所示。从图中可以得出,箍筋间距由80 mm增加到100 mm、125 mm时,弯矩由44.59 kN·m增加到44.60 kN·m、44.70 kN·m,分别增加0.02%和0.25%。当箍筋间距由80 mm增加到100 mm、125 mm时,刚度由2.76(kN·m)/mm减小到2.75(kN·m)/mm、2.65(kN·m)/mm,分别减小0.4%和4.0%。可见,箍筋间距对承载力以及刚度无显著影响。

图14 不同箍筋间距下弯矩-挠度曲线Fig.14 Influence of s on M-Δ curves
由此可以得出对圆中空钢管混凝土叠合构件抗弯承载力影响较大的参数依次是钢管直径、混凝土强度、纵筋强度、钢管厚度。对刚度影响较大的参数依次是混凝土强度、钢材强度以及纵筋强度。
4 纯弯承载力公式
基于叠加原理和极限平衡原理,可以将圆中空钢管混凝土叠合构件的抗弯承载力分为钢管和钢筋混凝土两部分。为了方便计算钢筋混凝土部分的弯矩,可以将圆空心钢筋混凝土截面等效为类“工”型截面,等效截面如图15所示。

图15 外包钢筋混凝土等效截面Fig.15 Cross-section simplification
根据文献[14-15],钢管部分的弯矩Ms计算见式(1),钢筋混凝土部分正截面纯弯承载力MRC计算见式(2):
MS=kfysAsd.
(1)
(2)
式中:Ae为混凝土等效应力块面积;Ali为单根钢筋面积;xc为混凝土等效应力块形心到受压边缘高度;xli为纵筋到受压边缘高度;σli为纵筋到应力。
运用线性回归计算得到m1=2.522 7、m2=2.522 7、m3=1.581,代入式(1)得:
k=2.522 7(d/D)2-3.714(d/D)+1.581。
应用叠加原理将式(1)与式(2)两部分的弯矩值叠加可以得到圆中空钢管混凝土叠合构件抗弯承载力计算式:
Mu=MS+MRC.
(3)
试验试件CB1~CB3的承载力公式计算值Muc与试验值Mue结果见表2。由表2可以得出,Muc/Mue的平均值和均方差分别为0.995和0.115,对比结果如图16所示。从图中可以看出,对比结果服从正态规律分布,Muc/MuFEM达到置信水平95%时的置信区间为(0.875,1.117)。

图16 公式计算值与试验值对比Fig.16 Comparison of formula with experimental values

表2 试验计算结果Table 2 Calculation results of test specimens
因为试验数据有限,笔者通过有限元软件变换不同参数验证上述公式的准确性。承载力计算值Muc与有限元模拟值MuFME结果见表3。从表3可以得出,Muc/MuFEM的平均值和均方差分别为0.993和0.050,对比结果如图17所示。从图中可以看出,对比结果服从正态规律分布,Muc/MuFEM达到置信水平95%时的置信区间为(0.964,1.036),因此公式可以满足实际工程。

表3 模拟计算结果Table 3 Calculation results of FEM specimens

图17 公式计算值与模拟值对比Fig.17 Comparison of formula with FEM values
5 结 论
(1)应用有限元软件模拟计算得到圆中空钢管混凝土叠合构件的弯矩-挠度曲线,有限元计算结果与试验实测结果偏差平均值为6.2%,结果吻合良好,有限元模型正确。
(2)圆中空钢管混凝土叠合构件纯弯破坏模态与钢筋混凝土构件的纯弯破坏模态基本相同,受压区混凝土压碎,受拉区钢筋、钢管屈服为构件的界限破坏准则,截面应变符合平截面假定。
(3) 钢管直径每增加25%,抗弯承载力平均减小4.8%,刚度无明显变化;混凝土强度每增加35.6%,抗弯承载力平均增大7.9%,刚度平均增大5.0%;纵筋强度每增加22.2%,抗弯承载力平均增大7.8%,刚度平均增大13%;钢管厚度每增加50%,抗弯承载力平均减小2.1%,刚度无明显变化。
(4)笔者推导出圆中空钢管混凝土叠合构件纯弯承载力计算公式,公式计算值与试验值结果吻合较好,可应用于实际工程。

