偏心受压作用下工字梁超声测试稳定性研究
郑 罡,杨 也,郭增伟,陈伟基,廖 伟
(重庆交通大学土木工程学院,省部共建山区桥梁及隧道工程国家重点实验室,重庆 400074)
超声应力测试一直是无损应力检测的重要研究方向之一[1]。D.S.Hughes和J.L.Kelly[2]于1953年提出声弹性的概念,此后的半个多世纪,研究人员[3-5]证明了超声波速和波幅与混凝土应力均存在相关性。混凝土内部的非均匀性会使超声波进入多重散射状态[6-8],这将影响直达波波速的准确测量[9],从而导致以直达波为研究对象的技术手段受到影响。进入21世纪以来,超声应力测试技术有很大进展,R.Snieder等[10]提出尾波干涉法(Coda Wave Interferometry,CWI)着眼于利用尾波(多重散射状态的超声波)对介质变化的高敏感性,后续研究[11-13]也表明可利用CWI观测混凝土试块的应力变化。但是,E.Niederleithinger等[13]也指出CWI在区别波形类别、判断方向性及预估测量上限等存在诸多制约。
为解决上述问题,近年来已有不少进展。2015年,E.Niederleithinger等[14]尝试引入平方相关系数(R2)与外加应力关联;2017年,A.Hafiz等[15-16]在将平方相关系数(R2)应用于尾波的全波形,研究发现幅值平方相干性(Magnitude-Squared Coherence,MSC)与施加应力有关。据此,可以发现全波形研究是一种符合逻辑的研究思路[17],文献[18]中已初有体现,笔者同样基于奇异值分解与高维空间投影建立了超声全波形与混凝土梁荷载之间的线性关系。
从文献[18]可以看到超声测试的应力指标存在一定程度的波动,其影响了测试结果的准确性,因此有必要对应力指标波动的来源进行研究分析。笔者将测试数据分解为荷载特性波形和残差波形,两者之和即为测试记录波形,同时对三类波形的测试稳定性进行分析,此处测试波形的稳定性是指重复试验下测试数据本身的可重复性。基于此,笔者设计实施了相关试验方案,由不同荷载等级的波形矩阵构造了一个荷载特性向量,通过该特性向量与波形向量的方向余弦提取归一化荷载指标,分析超声数据及荷载识别结果的直方图与统计参数,为后续的改进测试方法提供量化依据。
1 试验系统
偏心受压工字梁超声测试中,试验系统由混凝土工字试验梁、偏心受压加载系统和超声测试系统三部分组成,总体布置示意图如图1所示。支座采用C30素混凝土块,其长边外缘与梁体两端横截面对齐;换能器发射端布置于梁体一侧横截面中心,接收端布置于梁体另一侧,如图1所示(图中尺寸以mm计)。

图1 试验系统总体布置示意图Fig.1 Test system
试验梁采用的工字梁与文献[18]的工字梁同批次浇筑,长2 m,高0.45 m;顶底板宽30 cm,厚10 cm;腹板高25 cm,厚10 cm;混凝土标号为C30;配筋如图2所示[18]。

图2 工字试验梁配筋图Fig.2 Reinforcement detail
偏心受压加载系统包括加载部分和荷载控制部分,加载部分由粗钢筋和千斤顶组成(见图1),荷载控制部分则由应变仪以及压力环组成。
超声测试系统包括RSM-SY5(T)型超声检测仪、JHP01型换能器、导线和耦合剂等。采用一发双收方式采集超声数据。
考虑到换能器的固定性会影响超声波信号波形的稳定性,超声波信号幅值会随换能器荷载增大而趋于稳定[19],为保持超声测试中波形的稳定,采用环氧树脂作为耦合剂。同时参考文献[18]中的仪器参数并多次反复调试,确定了本试验中采样长度、采样间隔、脉宽、触发延时、跨距、发射电压、增益等7个参数,如表1所示。

表1 仪器参数设置Table 1 Instrument parameter setting
2 工况设计及实施
2.1 基本工况设计
笔者研究一天内混凝土工字梁不控制温湿度等条件下的超声测试稳定性,环境温度波动范围大致为5 ℃,相对湿度波动范围大致30%。在此条件下,设计了相应的基本试验工况,如表2所示。为尽可能使测试结果可靠,共进行了3次试验。注意误差因素的研究并非笔者的研究重点,具体干扰因素的研究将另行撰文分析。

表2 基本工况设计表Table 2 Basic design condition
工况设计初期参考了前期取得的一些经验基础,制定了7时段超声测试方案,后两次试验在前期试验基础上再补充7时段的超声测试,是为了考虑研究超声测试在一天之内更长时间的稳定性问题。但现有14时段的超声测试数据不够充分,故笔者聚焦于最基础的前7时段试验,后续补充测试数据再另行讨论。
2.2 试验过程与数据采集
一次完整的试验工况由连续20天超声测试组成,每天记录单级荷载下7时段的原始数据。超声试验时的预备状态为混凝土工字梁仅受其自重的状态,受力状态则为受其自重和偏心受压荷载作用的状态。

具体试验过程如下:
(1)将试验梁在预备状态静置1 d,待试验系统稳定,进行加载。
(2)混凝土工字梁加载1 kN偏心压力,进行该偏心受压加载状态下的超声测试。测试前对测试仪器预热1 h,待加载系统和仪器示值均稳定时正式进行测试。
(3)每天进行7个时段测试,每个时段仪器完成400次重复移点读数(采集),测试结束加载维持至第2天。
(4)与1 kN偏心压力加载超声测试相同,从第2级荷载(2 kN)到第20级荷载(20 kN)逐天增加偏心受压荷载并进行相应的超声测试,累计完成20级荷载的超声测试。
加载制式与过程示意图如图3所示。

图3 加载制式与过程示意图Fig.3 Schematic diagram of experimental flow
3 数据处理及测试方法
3.1 数据预处理
为了消除不同评价指标之间的量纲影响,需要进行数据零均值化和能量归一化处理,使数据指标之间具有可比性。零均值化与归一化实质就是空间的平移与缩放。零均值化是指变量减去其均值,实质为一个平移过程,平移后所有数据的中心为0。能量归一化是指变量除以自身的能量,这里简称归一化,实质是滤去超声数据的能量。
笔者的研究对象为全波形,原始数据都需进行零均值化与归一化处理[17]:1)去除波形中明显的异常点(最后一个点);2)对每级荷载下7时段的400条超声记录进行平均处理;3)对每级荷载的7条平均波进行零均值化;4)对去均值后的波进行归一化得到预处理后的波形,称作记录波形。
对原始数据进行预处理,每级荷载将得到一个1 023×7的二维超声矩阵,以第一次试验第1级荷载的7条记录波形为例,如图4所示。

图4 第一次测试第1级荷载的7条记录波形Fig.4 Seven pre-processed waveforms of the first test for level 1 load
经预处理两接收端均得到一个1 023×20×7的超声数据矩阵,记为Wj(j=1,2),称其为记录波形矩阵。由于两接收端的处理结果基本一致,后文仅选用接收端1的数据矩阵W1作分析示例,下文将W1简写为W。
3.2 高维空间投影
高维空间投影方法即根据实际需要,事先确定一种能衡量投影是否有意义的指标,即投影指标,通过某些函数把特征向量映射到高维空间(一般情况下高维空间上比低维空间上更加线性可分),建立起测试对象(荷载)与映射指标(投影)之间的联系。

(1)
其中,Σ为奇异值中的特征值矩阵。

qx=wlUΣVT.
(2)
其中,qx为基准向量[0.05,0.1,…,1],目的是建立超声信号与偏心受压荷载之间的线性拟合关系,对应测试荷载等级1,2,…,20。
再对式(2)两边进行右乘运算,可得特性向量wl:
qx(VT)HΣ-1UH=wl.
(3)
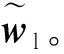
(4)

(5)
(6)
此时记录波形经过高维空间投影可以分解得到两个分量,其中一个是特性向量方向上的投影分量,即荷载特性波形,简称特性波形。另一个分量是记录波形与特性波形在特性向量法向上的差量,称为残差波形。
4 超声测试统计特性
由图4可看出7时段的波并不完全重合,这是由于试验过程中各种干扰的影响。这里将平均波认为是波形中不变的部分,即信号部分;各时段波形与平均波之间的误差认为是波形中的噪声部分(误差均未区分荷载等级)。
20级荷载下的记录波形,特性波形与残差波形都有一个1 023×7的二维超声波形矩阵,因此波形误差的样本空间n为143 220(1 023×20×7),为了直观表现出的波形误差以及噪声比例的分布情况,对其进行频数统计,选择2n2/5作为样本空间分组规则[20],目的是使卡方检验最大化发挥作用。为了更好对比三次试验的频数分布,将3次试验的误差样本进行合并确定组距,总的波形误差样本空间按上述分组规则可分成359个子区间。
分别对记录波形,残差波形及特性波形的误差进行统计分析。整体的分析流程如图5所示。
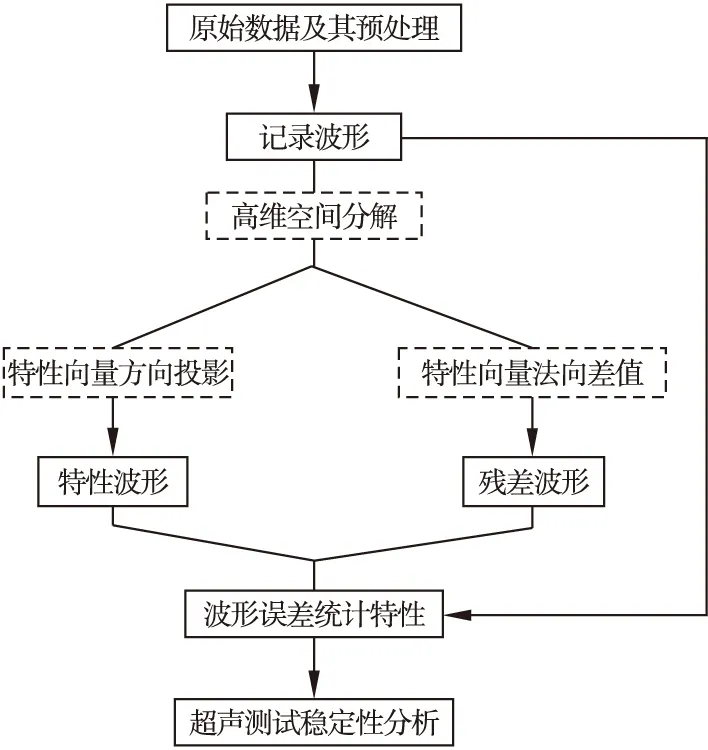
图5 整体分析流程Fig.5 Process of comparison and analysis
4.1 归一化荷载指标


图6 3次试验各时段的荷载指标Fig.6 Load indicators of different test terms
由图6可看出:①各时段试验的归一化荷载指标随荷载等级x呈良好的线性特性;②不同时段归一化荷载指标沿各自与荷载等级的线性关系曲线有小幅度波动;③第3次试验的荷载指标波动比前两次幅度大。
分析图6数据可知,第一次试验的归一化荷载指标最大误差在满量程的4.0%,第二次试验的归一化荷载指标最大误差在满量程的3.1%,第三次试验的归一化荷载指标最大误差在满量程的11.0%。
4.2 波形误差统计特性
统计记录波形的波形误差分组结果并绘制其频数直方图,用正态分布函数进行拟合,采用Levenberg-Marquardt优化算法解决拟合中的非线性最小二乘法问题,为了表现误差直方图均值附近的细节,y轴采用对数log10坐标,如图7所示。同时,为便于横向对比,将记录波形、残差波形以及特性波形的测试误差频数直方图绘制在一起,由于三次试验的结果基本一致,故仅以第一次试验为例,如图8所示。

图7 3次记录波形测试误差频数直方图Fig.7 Error histogram of pre-processed waveform

图8 三类波形测试误差频数直方图Fig.8 Error histogram for the first test of three types of waveforms
对波形误差的概率分布进行χ2检验[21],均不接受正态分布。由图8可以看出,波形误差的概率分布在均值附近与正态分布相差较大。这里采用峰度与偏度比较其与正态分布的差异,正态分布的峰度为3,偏度为0。试验中三类波形的测试误差分布的峰度均为30左右,约为正态分布峰度的10倍,偏度在0附近,说明波形误差以均值为对称轴左右对称且远偏离正态分布。
测试误差的统计特性及不确定度如表3所示。不确定度评定是计量领域的常用做法,引入测量不确定度将在很大程度完善整个测试过程,使测量结果更具科学性。A类评定是对重复观测的样本数据进行的不确定度分量评定;B类评定是基于文本资料规定的不确定度分量评定。这里主要采用A类评定对多次测试误差进行统计分析,测试误差的标准不确定度为

表3 三类波形的测试误差统计特性及不确定度Table 3 Statistical characteristics and uncertainty of test errors for three types of waveforms
U=k·UA=2·UA.
(7)
式中:UA为通过A类方法评定的不确定度;包含因子k=2。以第一次试验记录波形的标准不确定度为例:U=2×3.45×10-3=6.90×10-3。
波形经过零均值化,数据中心本在0处,但由于计算机连续计算产生的截断误差的累积,误差均值为极小的一个量值,这里统一记为0,并且不列入表里。用E表示波形误差,包括记录波形误差Es,残差波形误差Er和特性波形误差El三类误差;而Estd为E的标准差,Emin为E的最小值,Emax为E的最大值;U表示波形误差的标准不确定度。
由表3可以看出,记录波形被投影至高维空间特性向量方向上后,与荷载相关的特性波形不确定度相较残差波形减小了一个数量级,表明噪声占比大幅降低,荷载识别过程基本保持稳定,同时也表明算法具有一定的抗干扰能力。通过算法将噪声影响过滤到可接受的范围是可以接受的做法。
尽管特性波形的标准不确定度相较其他两个波形均低一个数量级,但第三次试验的归一化荷载指标最大误差仍然达到了满量程的11.0%。表明算法虽然具有一定的抗干扰能力,但噪声有时在特性方向上仍具有较大影响,通过高维空间投影亦无法对其进行滤除,因此仍需加强对试验条件的控制。
5 结 论
(1)通过对特性向量零均值化及归一化,将记录波形投影至新的特性向量上构造了归一化荷载指标,该指标其经过平移与放缩可还原为应力指标。
(2)通过波形的误差直方图分析工字梁超声试验的测试稳定性,记录波形与残差波形的测试误差标准不确定度在同一数量级,而特性波形比前两者均低一个数量级,这也是归一化荷载指标保持稳定的主要原因。
(3)荷载测试结果只与超声波形在高维空间特定方向上的投影相关,若其噪声较大,在该方向上的投影较小,则测试结果波动较小;若噪声较小,但集中于上述特定方向,则测试结果也将受到较大影响。

