单面受火的方钢管约束钢筋混凝土柱耐火极限

张玉琢，张 赫，王亚峰，徐 倩

(1.沈阳建筑大学管理学院，辽宁 沈阳 110168；2.辽宁工程技术大学土木工程学院，辽宁 阜新 123000)

钢管约束钢筋混凝土柱是一种结合了普通钢筋混凝土柱和钢管混凝土柱的新型钢-混凝土组合构件，其特点是梁柱节点处的钢管不相连接，钢管无需承受纵向力，仅对内部的混凝土起约束作用，使混凝土处于良好的三压受力状态，其在超高层及大跨度建筑结构中的应用愈加广泛[1]。钢管约束钢筋混凝土柱不仅在常温状态下具有良好的变形能力、其抗震性能，抗火性能也十分优异[2]。相较于钢筋混凝土柱，钢管约束钢筋混凝土柱在受火时可以约束混凝土保护层使之不会因受火而脱落，进而能够避免钢筋直接接触火焰从而不会因高温导致构件承载力骤降[3-5]。

延睿[6]以受火时间、截面尺寸、材料强度、含钢率和配筋率为主要参数，对6组共计18根方钢管约束钢筋混凝土短柱的进行试验，研究表明方钢管角部位置处的约束效果明显。Wang Xuanding等[7]以宽厚比、偏心率和翼缘加强方式为主要参数，试验包括12根偏心受压方形钢管约束钢筋混凝土柱，研究其传力机制及翼缘加强有无对其力学性能的影响，提出了该类构件简化计算式。孙墨林[8]以钢管径厚比、钢管强度、配骨形式为主要参数，进行了10根方钢管约束型钢超高强混凝土短柱轴压试验，对该类构件进行破坏分析，研究构件承载力及钢管受力状态。

在实际发生火灾时，由于构件或维护墙体的影响，可能出现多种受火方式。吕学涛[5]、张玉琢等[9]进行了非均匀受火的方钢管混凝土柱耐火极限研究。研究表明：非均匀受火，特别是单面受火方式下，由于柱截面升温过程呈现单轴对称分布；温度中心偏向受火面，致使受火面材料高温劣化程度剧烈，与均匀受火方式存在较大差异，最终耐火极限呈现差异。但目前尚无关于单面受火的钢管约束钢筋混凝土柱在耐火极限方面的研究。基于上述分析，笔者运用ABAQUS软件建立有限元分析模型，研究单面受火的方钢管约束钢筋混凝土柱在一定参数范围内含钢率、配筋率、荷载比、荷载偏心率等对构件截面温度及其耐火极限的影响规律，以期为实际工程提供理论数据。

1 有限元模型建立

1.1 温度场模型

温度场相关模型中全部采用热分析单元。钢筋为两节点传热索单元(DC1D2)，钢管为四节点传热四边形壳单元(DS4)，混凝土采用八节点传热三维实体单元(DC3D8)。本模型中试验柱不与墙体接触的一面单面受火，与墙体相连的三个面简化为非受火面。受火面钢管表面通过表面辐射和表面对流模拟外界环境。受火面按第三类边界条件考虑，设置综合辐射系数为εr=0.8×0.625=0.5，受火面对流传热系数为αc=25 W/(m2·℃)；背火面也按第三类边界条件考虑，对流传热系数为αb=9 W/(m2·℃)[5]。钢管内表面和混凝土之间的接触面采用S-S接触。钢管与混凝土之间存在界面空隙,可能夹杂水蒸气、空气等介质，使钢管与混凝土界面间形成热阻[5]。参照文献[5,10]中对54个钢管混凝土温度场接触热阻的研究结果，取0.01(m2·℃)/W[10]。混凝土与钢筋之间的约束通过tie的形式实现。同时，参照T.T.Lie[11]的建议,模型中混凝土、钢材的热工参数按照文献[11]选取。混凝土硬化后残余的水分，按照混凝土质量5%考虑，且ρw·cw=4.2×106J/(m3·℃)。

1.2 耐火极限模型

耐火极限模型是建立在温度场模型之上的，对于混凝土高温下压应力-应变模型选取文献[11]建议的模型。

高温下混凝土受拉应力-应变模型参照S.Hong等[12]提出的模型。

规范《BS EN 1992-1-2:2004》[13]规定了高温钢材本构关系模型及折减系数，泊松比取用0.30，文中钢材本构模型据此选取。

在耐火极限的模型中，混凝土采用八节点三维实体单元(C3D8R)、钢管选取四节点壳单元(S4R)、钢筋用二节点索单元(T3D2)进行模拟。混凝土和钢管仍按照1.1节中方法模拟二者的相互作用。钢筋通过嵌入约束来模拟在混凝土中的工作情况。在混凝土上下端表面设置参考点，并与混凝土用Rigid body绑定，将构件的荷载及边界条件施加在上下两端参考点上以模拟试件实际受荷情况。

1.3 模型验证

利用所建立的温度场有限元模型，对文献[6]中试件编号S250-45、S250-90的方钢管约束钢筋混凝土短柱(均匀受火条件)试验结果进行验证。同时，对文献[3]和[5]中的试件进行验证,模拟结果吻合良好。

2 典型试件算例

2.1 温度场有限元模型及参数

以正方形截面边长为300 mm，含钢率为3%对应钢管厚度ts=2.25 mm的构件为典型算例，进行单面受火时升温120 min的温度场分析模拟。混凝土中配置的纵向钢筋为8Φ22。构件的受火方式及几何参数如图1所示。构件截面不同位置的温度-时间曲线如图2所示。

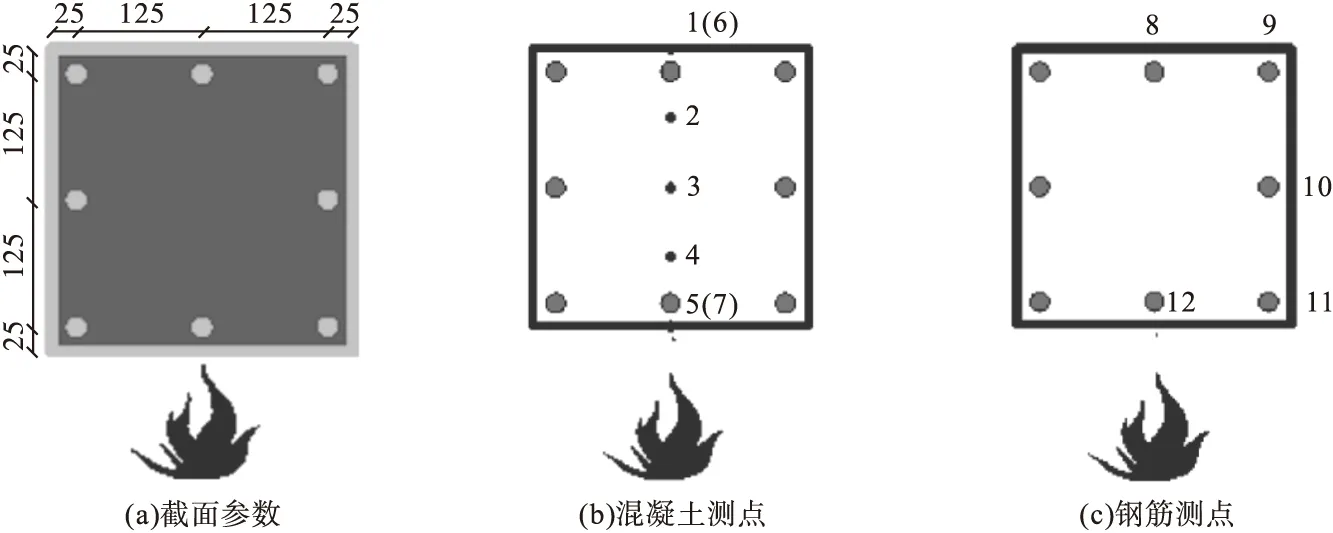
图1 截面设计参数及受火方式示意图Fig.1 Design parameters of cross section and fire form

图2 构件截面各测点处温度-时间曲线Fig.2 Temperature-time curve of different test points in component section

由于模型中考虑了钢管和混凝土之间的界面热阻，因此在同一点的钢管温度高于混凝土，二者表面温度的差异是点面接触的随机性导致的。受火面混凝土温度(最高)与核心处温度(最低)温差为+770 ℃。根据图2中测点5、7、12在30 min、60 min、90 min、120 min处对应的温度值可知，混凝土保护层处的温度值远高于钢筋的温度。受火时间小于30 min时，纵筋热膨胀影响较大，钢材强度损失较小，纵筋承受荷载增加，压应力也增大。能够使核心混凝土在钢管受火失效以后仍能坚持承载。

由图2可知，受火面角部钢筋温度最高，这是因为角部钢筋向构件内部非受火区域传递热量的范围为沿钢筋轴心180°。在构件角部位置，受火面对相邻非受火面混凝土保护层处有热传递、热辐射及热对流的影响，在角部25 cm×25 cm的范围内为受火面作用区域，虽然角部钢筋向非受火区域传递热量的范围也为180°，但是由于沿角部位置钢筋轴心截面左右两侧温度场分布不均匀，右侧为非受火面，混凝土厚度25 cm，传递热量相对截面中部的混凝土少。混凝土测点2、3、4的温度要比混凝土测点1低，这是由于混凝土的导热系数要远低于钢材。

图3为不同时刻构件截面温度分布云图。由图3可知，构件在升温过程中，等温线沿受火面中线呈单轴对称分布。受火面一侧温度较高、升温较快，而背火面与之相反，这是因为背火面的热量通过钢管、混凝土热辐射及热传导传递，导热系数相对较低。升温时间在30～120 min时，试件应力云图在受火面及其相邻非受火面的角部位置均沿试件对角线对称分布，与图2得出的钢筋温度变化规律一致。

图3 不同时刻构件截面温度分布云图Fig.3 Temperature distribution nephogram of component section at different time

2.2 力学场

计算力学场时，选取试件截面边长300 mm，厚度ts=2.25 mm，含钢率为3%，与温度场保持一致，使有限元模型在计算时能够较好的模拟试件在火灾下的受力模式，力学场模型中混凝土选取fcu=30 MPa且钢管及钢筋选取fsy=345 MPa。经过计算得出该构件在常温状态下的极限承载力为3 620 kN。荷载比n取0.6，即计算火灾下模型中实际施加的恒定轴压荷载为2 172 kN。

图4为构件轴向位移-时间的关系曲线。由图4可知，在构件升温初期，构件受热膨胀变形要小于构件受压导致的变形，因而没有产生正位移(构件轴向膨胀为正)。随着温度不断升高，构件的力学性能不断降低，构件轴向变形不断增大，最后构件轴向变形速率骤然加大，直到构件破坏。

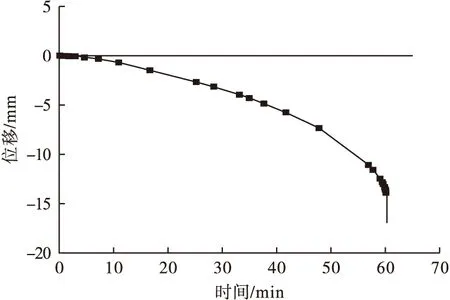
图4 轴向位移-时间关系Fig.4 Relationship of axial displacement and exposure time

图5为约束钢筋混凝土柱跨中位置处挠度-时间曲线，跨中挠度朝向受火面方向为正方向。图5表明，在受火初期构件因受力压缩向背火面挠曲，随着受火时间延长材料力学性能退化，直到构件发生破坏前，跨中挠曲速率不断增大。因荷载比n=0.6偏大，并且构件受火面积较小，构件热膨胀变形较小，由始至终均为全截面受压。

图5 侧向挠度-时间关系Fig.5 Relationship of lateral deflection and exposure time

图6为构件跨中截面混凝土应力分布云图随时间的变化情况，云图下部为受火面。当t=0 min时加载完毕，混凝土全截面受压，角部处应力稍大。受初始缺陷影响构件截面上半部分压应力大于下半部分，向受火面挠曲；在t=10～40 min过程中，由于受火面温度不断升高导致材料性能退化，混凝土内部压应力最小区域由受火面逐渐向背火面(背火面为受火面正对的面)移动；当升温至55 min时，构件的挠曲方向为背火面方向，混凝土应力最小区域开始缩减并不断向背火面靠拢；当升温至60 min时，混凝土压应力最小处位于背火面边缘，受火面压应力不断向内部蔓延，由于荷载比较大(n=0.6)，全过程中混凝土截面均未出现拉应力。

图6 不同升温时间混凝土应力分布 Fig.6 Stress distribution of concrete section at different time

图7为不同时刻钢管Von Mises应力分布云图，当t=35 min时，钢管全截面受压，且向背火面挠曲趋向明显。当t=50 min时，受火面钢管呈横向条状高应力区，背火面应力集中现象由角部向中部靠拢。当构件达到耐火极限即t=60 min时，构件发生整体失稳破坏,并伴随多波屈曲现象。

图7 不同升温时间钢管 Von Mises 应力分布云图Fig.7 Stress distribution nephogram of steel tube Von Mises at different time

3 参数分析

高温作用时，构件耐火极限可能与试件含钢率α、配筋率ρ、荷载比n、荷载偏心率e/i。按表1的取值范围，以其中参数为依据建立有限元模型，探究上述参数对约束钢筋混凝土柱耐火极限规律的影响[15-16]。

表1 参数分析取值范围Table 1 Range of parameters

3.1 含钢率

耐火极限随含钢率的变化由图8所示。耐火极限随含钢率增加呈现先略有上升后下降的趋势。当n=0.5时，含钢率从3%的初始值，当升高到4%，时构件耐火极限上升了4.2%；当升高到5%时，耐火极限下降了4.3%；当升高到6%时，耐火极限下降了6.2%。含钢率越大，钢管对核心混凝土约束作用越强，致使构件常温极限承载力增强有利。当含钢率增幅较小时，其约束作用对构件耐火极限的有利影响要大于受火导致材料力学性能退化产生的不利影响，构件耐火极限增大。当含钢率大幅上升时，因钢管直接受火，其高温力学性能退化明显，钢管的承载力下降较快，其不利影响大大超过其有利影响，因此耐火极限下降明显。而含钢率不变时，荷载比的增大会使构件的剩余承载力降低，引起耐火极限的下降。

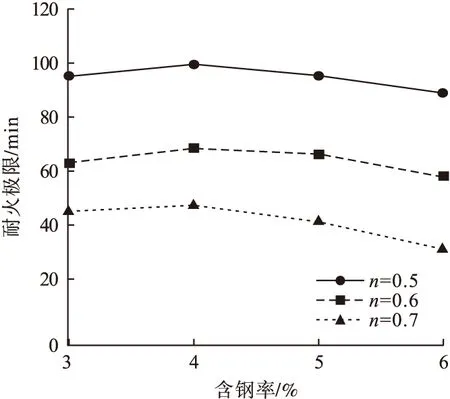
图8 含钢率对耐火极限的影响Fig.8 Influence of steel ratio

3.2 配筋率

图9为配筋率对构件耐火极限的影响。构件耐火极限随着配筋率由1.37%增加至4.02%，整体呈现上升的趋势。当n=0.6时，配筋率由1.37%升高到2.26%，构件耐火极限上升了8.50%；配筋率从2.26%升高到2.79%，构件耐火极限上升了7.13%；配筋率从2.79%升高到4.02%，构件耐火极限降低了2.20%。配筋率增加提高了构件对于纵向力的承受能力，进而略微提高了构件的耐火极限，但其对耐火极限的提升有限，配筋率越高受高温影响越大，反而导致耐火极限无法继续升高。

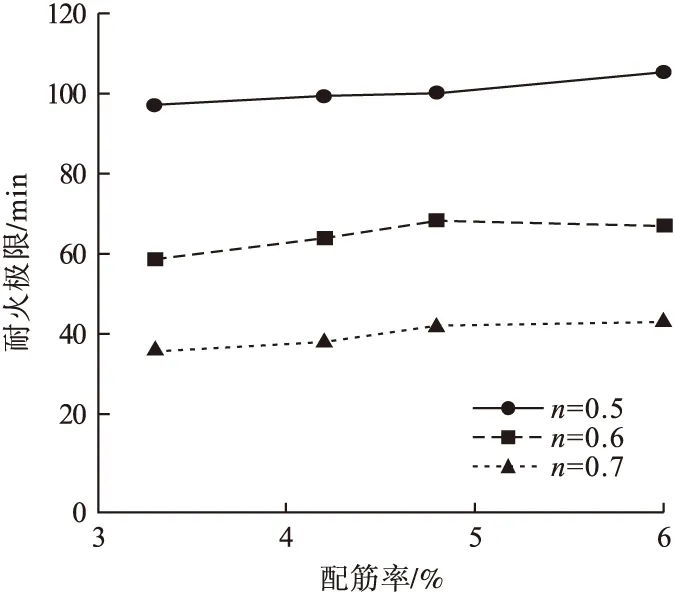
图9 配筋率对耐火极限的影响Fig.9 Influence of bar ratio

3.3 荷载偏心率

因单面受火的方钢管约束钢筋混凝土柱截面温度单轴对称，为研究荷载偏心率对构件耐火极限的影响，笔者沿构件y轴方向选取了荷载偏心率为0.6、0.4、0.2、0、-0.2、-0.4、-0.6的位置对构件进行加载，取偏向背火面方向为正，荷载偏心率对构件耐火极限的影响如图10所示。

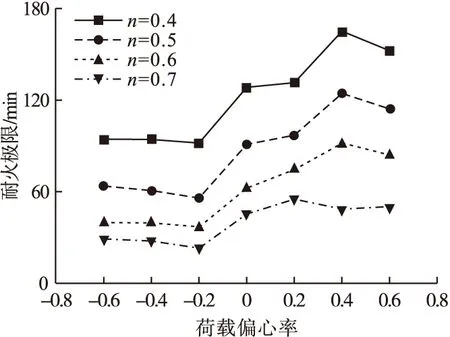
图10 荷载偏心率对耐火极限的影响Fig.10 Influence of load eccentricity

当偏心率为正时即偏心点位置偏向背火面时，构件的耐火极限会升高，这是因为单面受火的构件，构件截面温度场呈现单轴对称特点，在受火时间的持续增长的过程中，材料的力学中心不断从几何形心向背火面边缘偏移，所以当荷载作用偏向背火面时耐火极限会升高。当e/i=0.4时，构件耐火极限达到峰值，此时的荷载偏心率即为极强偏心率(耐火极限峰值点的偏心率)。当e/i>0.4时，构件因偏心导致的挠曲变形过大，耐火极限开始明显下降。e/i<0时，构件的耐火极限总体较低。这是因为当偏心点位置偏向受火面时，混凝土受压区面积变小，同时材料性能受高温退化的影响，因而耐火极限呈现下降趋势。

根据模拟结果可知荷载偏心率和荷载比对构件耐火极限的影响较为明显，当荷载比为0.4，偏心率由0到0.4时，耐火极限提升了28.8%，偏心率由0到-0.2时，耐火极限降低了28.41%；当荷载比为0.5，偏心率由0到0.4时，耐火极限提升了36.79%，偏心率由0到-0.2时，耐火极限降低了38.76%；当荷载比为0.6，偏心率由0到0.4时，耐火极限提升了47.94%，偏心率由0到-0.2时，耐火极限降低了40.98%。

4 结 论

(1)单面受火条件下的构件，构件横截面温度云图和应力分布云图均呈单轴对称分布，由于受火面一侧材料在高温下性能的退化，构件破坏时朝背火面挠曲，呈现整体失稳破坏态势。

(2)当荷载比较大时，构件在火灾下承受荷载过程中，混凝土截面呈现全截面受压，升温导致的热膨胀变形不明显；钢管纵向受压、环向受拉，并且最终会在受火面出现横向条状高应力带。

(3)荷载偏心率和荷载比对构件耐火极限的影响较大，配筋率和含钢率影响较小。荷载比越小耐火极限越大，当竖向荷载偏心率达极强偏心率时构件耐火极限达到峰值，且极强偏心率的影响因素较多分析较为复杂．建议方钢管约束钢筋混凝土单面受火时采用低荷载比n≤0.6，偏心受压点设置在背火面一侧。