基于村镇地震环境相关的区域地震动场模型研究

李宏男，陈艳辉，张 皓

(1.沈阳建筑大学土木工程学院，辽宁 沈阳 110168；2.大连理工大学土木工程学院，辽宁 大连 116024)

近年来，我国地震发生频繁，特别是西部的山区地带，不仅是地震多发区，而且其地震的频度、强度都很高，一旦发生强震将给当地居民的房屋造成巨大的破坏。李钢等[1]在汶川地震村镇建筑结构震害调查与分析中指出，以四川为代表的村镇地区建筑受地震影响的破坏形式众多，且存在不少的不同形式的转动破坏现象，由建筑物的自身转动引起。20世纪50年代，E.Rosenblueth[2]最先定性明确，地震动自身有摇摆分量存在。J.L.Stratta等[3-5]的研究都强调一个运动的摇摆分量对建筑物响应的可能影响。V.M.Graizer等[6-7]研究分析了均匀土层内的活动断层周围的转动分量，研究相对于平动分量存在的幅值来说，地震动转动分量的幅值是偏小的，但不应被忽略。H.N.Li等[8-9]通过研究发现，自身对称的建筑结构，存在的转动分量依然会造成建筑物发生扭转现象。G.C.Hart等[10]研究发现，对于跨度很大的结构，地震动转动分量是引起结构破坏的一个重要原因。由于当前观测仪器还是较难记录可在山区抗震计算的转动分量实测数据，所以通过定性理论分析，以平动分量为基础计算转动分量变得尤为重要。

一些学者对地震动存在的转动分量进行分析，试图以弹性理论为基础从平动分量间 接得到转动分量。1969年，N.M.Newmark[11]根据行波法，由地震动平动分量计算推导出地震动的扭转分量。从记录到的各分量中可以看出，地震造成地面振动是极其复杂的，任何形式的地震动都可以分解为多类频率并不一样的简谐波，称此方法为频域法。V.W.Lee等[12-13]使用该方法计算地震动理论存在的转动分量。李宏男等[14]对转动分量研究时进行了较大改进，并用实验验证了得到的转动分量的合理性。孙士军[15]等利用频域法，采用当地等效群速度实际曲线，并推导地震波入射角得到视波速，以此为基础由实际记录的平动分量计算得到符合当地的转动分量。此后，C.W.Cheng等[16-17]、D.Basu等[18-19]等基于弹性波动理论，分别提出了提取转动分量的新方法。

目前针对地震动各分量的频谱特性研究较少，前人在采用已记录到的平动分量来获得转动分量并不能完全满足山区村镇建筑抗震需要。基于此，笔者选择四川省平武县沙河村作为研究场地，通过概率法开展地震危险性分析，以其结果为设定条件合成地震动加速度时程。当震源较近时波传递以体波为主，因此可以根据震源的远近、场地情况等以某一类波为主要考虑因素。按照弹性波理论，体波和面波都与旋转有关，笔者选取近场地震，采用MATLAB程序计算转动分量，采用频域法对体波入射平动分量进行傅里叶变换。

1 区域地震活动性及主要断裂

1.1 地震活动性的空间分布特征

研究区域：东经102°30′～106°30′、北纬30°30′～34°30′。该区域主要涉及两个地震带：龙门山地震带和长江中游地震带。区域内历史地震的空间分布格局有两个主要特征：①地震活动的空间分布具有明显的不均匀性。主要表现在区域破坏性地震震中呈条带状分布，强震活动的这种特性则表现得更为突出；②区域地震活动与断裂构造的分布有着密切的联系。

1.2 研究区域的构造断裂

根据研究区域的地震地质资料、物理场情况与构造运动最新状态等要素，确定研究区域内的断裂活动情况。近场区处于川青块体的东边界附近，区内断裂构造较为发育，分布有龙门山断裂带、虎牙断裂、塔藏断裂等区域性活动断裂。

2 地震危险性概率分析

2.1 潜在震源区划分

在对研究区域的地震构造环境、地震活动特征等进行充分研究的基础上，根据潜源划分的构造类比和活动重复性原则，共划分出31个潜在震源。

2.2 地震带地震活动性参数的确定

地震带内大小地震的比例关系可以用震级-频度关系来描述：lgN(M)=a-bM。其中a、b为拟合的古登堡曲线系数。震级档间隔为0.5，计算各区带大于等于震级M累计发生次数，采用最小二乘法统计拟合，得到各区带的震级-频度曲线如下。

龙门山地震带：

lgN(M)=3.557-0.715M.

(1)

长江中游地震带：

lgN(M)=6.155-1.374M.

(2)

相应的震级-频度关系见图1。

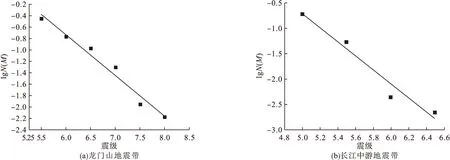
图1 震级-频度关系曲线Fig.1 The relation curves of seismic belt lgN(M)-M

地震年平均发生率v0根据地震带的实际地震活动历史和资料概括，用统计拟合得到龙门山地震带、长江中游地震带的b值和实际历史地震资料进行外推。各地震带的地震活动性参数见表1，表中R表示拟合相关系数。

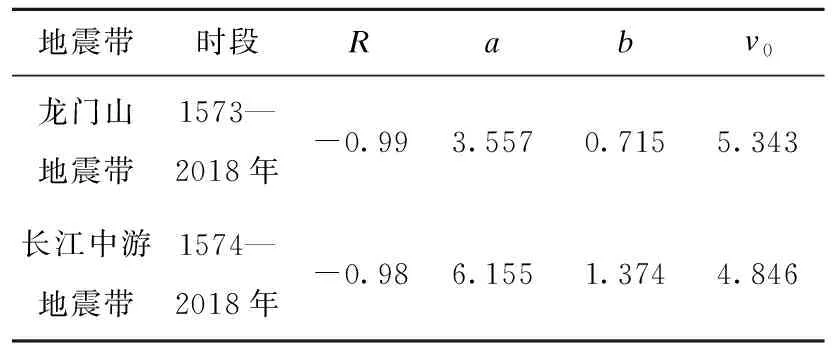
表1 地震带地震活动性参数Table 1 The activity parameters of the seismic belts

2.3 基岩地震动衰减关系

对于地震烈度和基岩水平峰值加速度的衰减关系来说，各个地区的地震震源发震特点、中间的传播介质和特定的场地情况均不一致，所以导致烈度地震动衰减关系存在着很大的地区差异性[20]。按照地震资料分别对衰减关系长轴、短轴进行统计拟合，得到适合本地区的烈度衰减关系及水平峰值加速度衰减关系(见图2)。

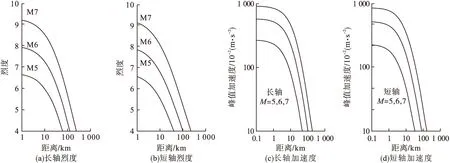
图2 西南地区地震烈度、基岩水平峰值加速度衰减关系Fig.2 Seismic intensity attenuation relationships and attenuation relationships of horizontal peak acceleration of bedrock in southwest China

2.4 地震危险性性概率计算结果

概率性地震危险性分析计算结果见表2，不同风险水平下的超越概率曲线见图3。

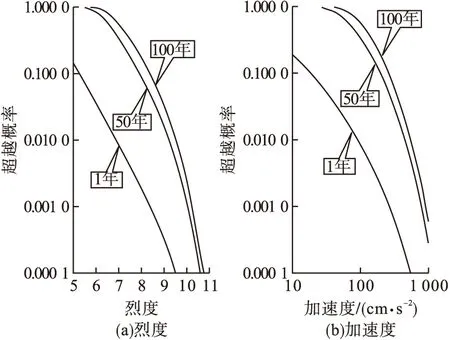
图3 场地烈度和基岩水平峰值加速度衰减超越概率曲线Fig.3 Curves of level peak acceleration of site rock and seismic intensity of the site rock under different exceeded probability level

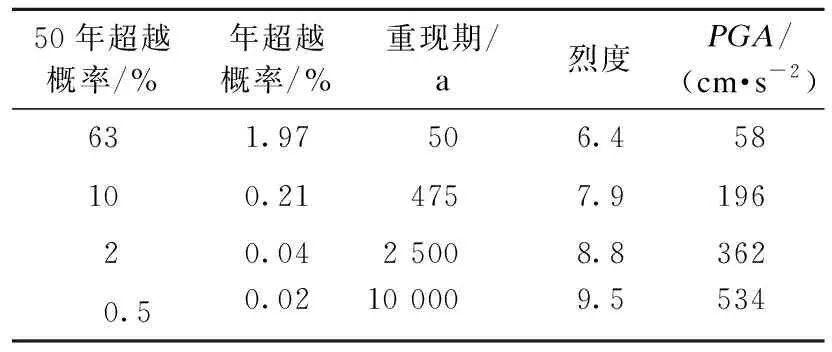
表2 地震危险性分析结果Table 2 The results of probabilistic seismic hazard analysis

图4为主要潜在震源区对场地地震危险性的贡献，从图中可以看出，贡献最大的潜在震源区为平武7.5级潜在震源区。场地50年不同超越概率下基岩水平向峰值加速度反应谱曲线如图5所示。

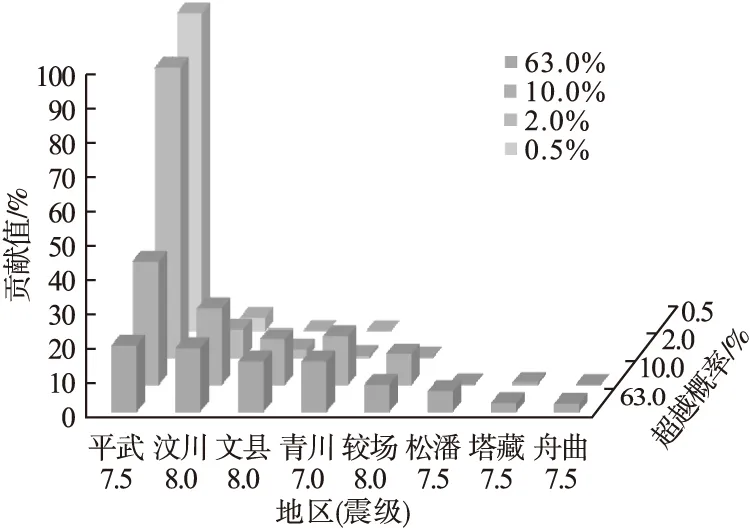
图4 主要潜在震源区对场地基岩水平峰值加速度的贡献分布图Fig.4 Map of contribute of the main potential seismic source zones to level peak value acceleration of the site rock

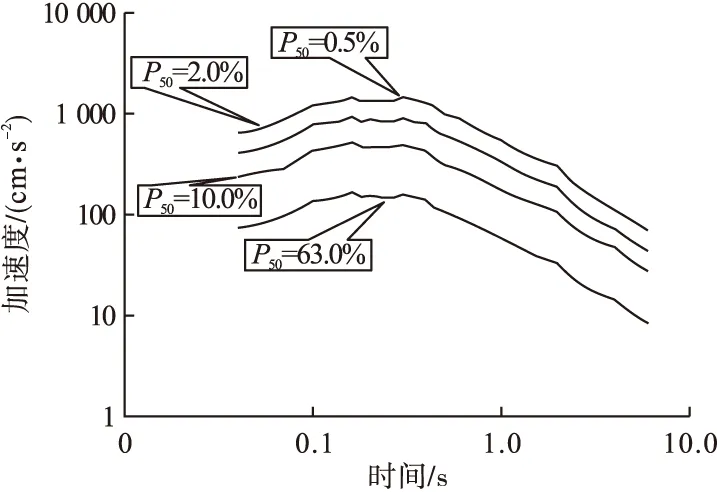
图5 50年不同超越概率基岩水平加速度反应谱曲线Fig.5 The response spectrum curves of level peak value acceleration of the site rock under different exceeded probability level in 50 years

在人工合成加速度时需要考虑震级大小和震中距，以此来推导加速度持时，选取地震危险性分析计算结果中重现期为2500年的抗倒塌罕遇地震动，理论等效震级为7.20，理论等效震中距为16.00 km。

3 多维地震动的合成

3.1 频域法

由大量强震震害以及理论推导可知，地震波传播到地面时造成的运动形式相当复杂，振动地面的各点不仅产生3个正交的平动分量，也产生3个转动分量。

地震记录不是简单的谐和振动，是随机振动幅值大小和频率均在不断复杂变化，但总能将其分解为简谐波(不同频率)组合而成。频域法基于这种思想，前人以已有的平动分量通过弹性半空间理论来计算转动分量，入射地震波假设只有体波。入射P波(SP)时，反射波有P波(SPP)和SV波(SSP)；入射SV波(SSV)时，反射波有SV波(SSS)和P波(SPS)；入射SH波(SSH)时，反射波仅有SH波(SSH)。

当震源较近时波传递以体波为主，因此可以根据震源的远近、场地情况等以某一类波为主要考虑因素。其中体波入射及反射坐标系见图6。按照弹性波理论，体波和面波都与旋转有关，笔者选取近场地震，利用编制的相应程序计算转动分量，采用频域法对体波入射平动分量进行傅里叶变换，所得结果可供山区多维地震动抗震提供参考。

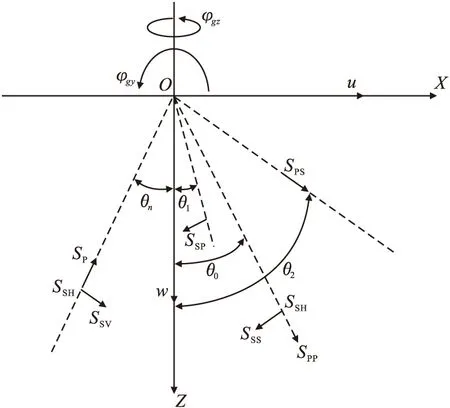
图6 体波入射及反射坐标系Fig.6 Coordinate system and reflections of P-,SV-,and SH-waves

不同频率的简谐波组成了地震波，体波频率为ω的P、SV和SH入射波，其位移函数为

(3)

(4)

(5)

反射波的位移函数分别为

(6)

(7)

(8)

(9)

(10)

其中，α、β分别为P波和S波的波速。

(11)

(12)

式中：λ和μ分别为Lame常数值；E为弹性模量值；ρ为质量密度；υ为泊松比。

按照shell法则，入射角值θ0与反射角值θ1和θ2的关系为

(13)

根据式(3)～式(10)，场地质点在x、y和z方向上的位移分量u、v和w分别为

u=cosθ0SSV-cosθ0SSS+sinθ0SPS+

sinθ0SP+sinθ0SPP-cosθ1SSP.

(14)

v=2SSH.

(15)

w=sinθ0SSV+sinθ0SSS+cosθ2SPS-

cosθ0SP+cosθ0SPP+sinθ1SSP.

(16)

以弹性波动理论推导得出，绕z轴的扭转分量和绕x轴、y轴的摇摆分量可以分别表示为

(17)

(18)

(19)

(20)

将式(5)和式(15)代入式(20)可得扭转分量为

(21)

摇摆分量为

(22)

因在自由表面(z=0)剪应力为零，即：

(23)

因此摇摆分量为

(24)

为了计算式(24)，需要求w的偏导数。为此利用式(3)、式(6)和式(10)，可得以下偏微分式：

(25)

利用式(16)、式(24)和式(25)可得：

(26)

当地面运动主要由剪切波组成时，绕y轴的摇摆分量为

(27)

式(21)和式(27)中：C为视波速。

对式(21)和式(27)做傅里叶变换得：

(28)

(29)

对已记录到的3个互不相关的平动分量时程进行傅里叶变换，将其幅值谱代入式(28)和式(29)可以得到转动分量幅值谱，然后将转动分量幅值谱进行傅里叶逆变换，就可以得出转动分量的角加速度时程。

3.2 确定视波速

由前面推导的公式可知，视波速C是以频域法为基础从已记录平动分量加速度时程来计算转动分量角加速度时程的关键参数。在实际发生的地震中，土层介质具有不均匀性，因此视波速C通常不为常数，其含义就是存在频散性。由于目前记录观测地震的现状发展，视波速C基本上是以统计大量地震波数据得到的，但各个地区地质条件及震源特性不同，所以视波速通常也是不一致的。因此在理论上的转动分量计算时需尽量采用对应地区和地震数据拟合的视波速频散曲线。鉴于以上考虑，笔者采用适合中国四川地区场地条件的视波速曲线，该地区地震波频散曲线的表达式及各参数如下：

C=[6.542+1.404log10f-

0.182(log10f)2](1+0.2ζ).

(30)

式中：ζ为(-1,1)的随机数；f为频率。

3.3 转动分量计算步骤

计算由地震波体波产生的转动分量时，可按以下步骤进行。

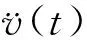
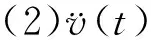
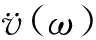
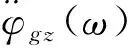
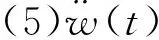
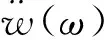
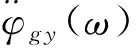
3.4 计算结果及分析比较

选取研究地区记录到的地震波数据，震级M=7.20，震中距R=16.00 km。利用上述计算转动分量的频域法，选取对应该地区的视波速频散公式，采用MATLAB软件编制相应程序由平动分量计算相应的转动分量。

为了便于对比分析，现给出地震动平动分量和转动分量的加速度时程曲线(见图7)。从图7可以看出，竖向分量峰值小于两平动分量，摇摆分量的时程曲线与扭转分量的时程曲线具有一定的差异性。地震波平动分量表现为EW分量及NS分量在中低频段更具频谱成分，而UD分量在高频段更具频谱成分；对于转动分量，摇摆分量幅值没有扭转分量在高频段频谱成分那样丰富；对比平动分量幅值谱和转动分量幅值谱可以看出，在高频段转动分量幅值谱相对于平动分量更加丰富，频带更宽，且随频率的增加衰减较慢。

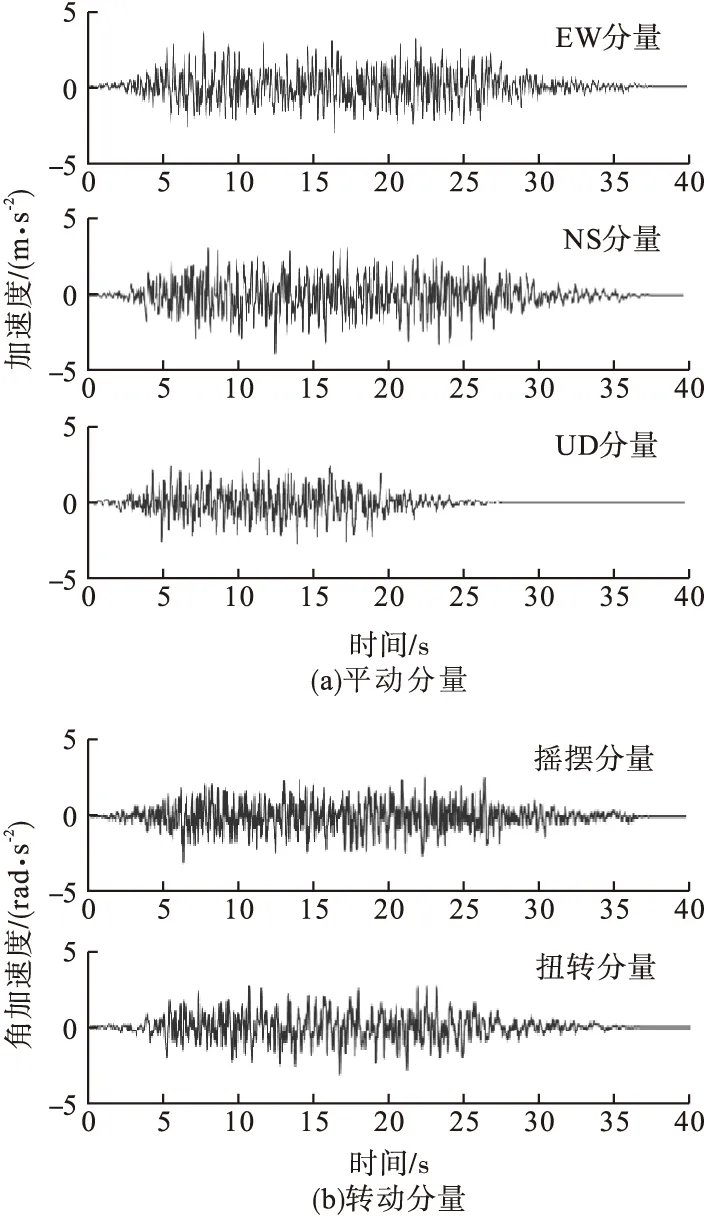
图7 地震动平动分量与转动分量加速度时程曲线Fig.7 Time history of translational acceleration and rotational acceleration

4 结 论

(1)在潜在震源区划分方案中，采用了三级划分，即考虑地震区带、背景源、构造源的共同影响，这对研究场地地震动危险性更具有合理性。通过对研究地区地震地质背景、发震断裂及其发震能力、地震活动的时空分布特征、未来50年地震活动趋势预测，给出各个风险水平下的设定地震，其结果可以为当地有关部门指定大震应急预案、建立大震快速反应系统提供依据。

(2)通过对研究场地进行地震危险性分析，得到场地的抗倒塌罕遇地震动计算结果：地震烈度8.8度，基岩水平峰值加速度362 cm/s2。选取等效震级M=7.20，等效震中距R=16.00 km，其中对场地影响较大的是平武潜在震源区和汶川潜在震源区。

(3)对记录到的平动分量，以频域法计算得到地震动转动分量，对其进行对比分析。转动分量傅里叶谱在高频段比平动分量更丰富，频带更宽，且随频率的增加衰减较慢，因此对于山区自振频率较高的居民自建建筑，抗震更应考虑转动分量对地震反应的潜在不利影响。