盾构管片衬砌纵向非均质等效连续模型
郭 乐 杨新安 邱 龑
(同济大学道路与交通工程教育部重点实验室,201804,上海//第一作者,博士研究生)
盾构管片衬砌纵向非均质等效连续模型
郭 乐 杨新安 邱 龑
(同济大学道路与交通工程教育部重点实验室,201804,上海//第一作者,博士研究生)
将盾构管片沿纵向分为环缝影响范围内、外两部分,环缝影响范围外取管片实际刚度,环缝影响范围内取等效刚度,环缝影响范围内、外连接处为刚性连接,推导出环缝影响范围内等效轴向刚度和等效弯曲刚度,并与等效连续均质模型的计算结果进行对比分析。提出了等效剪切刚度的概念。剪切刚度首先由管片接触面摩阻力提供,当剪切位移增大到螺栓与螺栓孔接触时螺栓参与抗剪,并推导出等效剪切刚度和剪切位移的计算式。讨论了环缝影响长度对各等效刚度的影响。
盾构; 管片衬砌; 纵向连续模型; 非均质; 环缝影响范围; 等效刚度
Author′s address Key Laboratory of Road and Traffic Engineering, Ministry of Education, Tongji University,201804,Shanghai,China
在盾构各施工阶段,管片衬砌在纵向上处于不同的受力阶段,如千斤顶推力、盾尾刷密封压力、上浮力,最终受到已固结浆液和地层压力共同作用[1-2]。同时,隧道作为带状结构物,由于多种因素(沿线地层差异性、使用荷载、偶然荷载等)的耦合作用,会产生纵向不均匀沉降,如上海市金山海水引水工程隧道[3]与上海轨道交通1号线[4-5]均已出现明显的不均匀沉降。为描述施工阶段和运营阶段管片受力及变形特性,提出合理的纵向计算模型非常重要。
日本学者提出两种管片纵向等效计算模型,一种是以村上博智及小泉淳为代表的梁-弹簧模型;另一种是以志波由纪夫及川岛一彦为代表的等效刚度模型。该方法认为隧道在横向为一均质圆环、在纵向以刚度等效的方法将有环向接缝非连续的结构等效为连续均质圆筒[3]。文献[6]通过模型实验与理论推导的方法,提出环缝影响范围,将管片宽度在环缝影响范围内、外分别计算,再通过环缝张开量将纵向刚度进行均质等效处理。文献[7]提出不均匀沉降曲线特征,基于文献[6]的纵向等效刚度解析公式,提出环缝张开量与纵向曲率的计算方法。文献[8]考虑横向刚度有效率,将隧道纵向等效为连续均质模型。文献[9]考虑横向变形为“椭圆形”,考虑环缝影响范围,并根据变形后的隧道截面得出适用性更广的纵向等效均质模型。文献[10]根据4种典型隧道纵向变形曲线,分别计算出剪力解析解。文献[11]采用弹性地基壳柱理论,对不均匀变形条件下隧道内力给出了解析解,并进行实例计算,分析影响隧道变形和内力的影响因素。文献[1]和文献[12]采用均质等效梁计算管片施工阶段纵向受力和上海长江隧道纵向弯矩与剪力。文献[4]和文献[13]通过数值模拟的方法描述管片纵向变形特征,计算出管片混凝土与螺栓受力,并将计算结果与文献[11]的解析解进行比较。
从管片纵向受力计算研究现状看,大部分学者采用纵向等效连续均质模型,并取得了一些成果。但实际上管片在纵向表现为非均质性,环缝接头与管段刚度存在明显差异,采用等效连续均质模型难以体现在环缝处刚度不连续的特点。本文将管片纵向等效为连续非均质模型(见图1),使环缝接头影响范围内刚度小于环缝接头影响范围外刚度,管片纵向在环缝处刚度不连续。现有模型中均未考虑环缝接头处剪切刚度的计算方法,所以本文提出环缝处等效剪切刚度的概念,等效剪切刚度可为计算相邻管片间因承受剪切力而产生的环间位移提供依据。
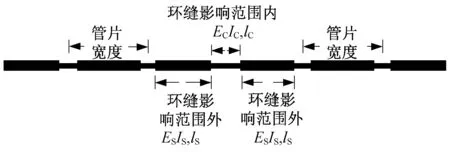
图1 管片纵向非均质等效连续模型示意图
1 模型的建立
建立管片纵向非均质等效连续模型时认为管片横断面为均质圆环,沿纵向连续,但考虑管片环缝接头处刚度偏小的特点,沿纵向将管片划分为环缝影响范围内、外两个部分;环缝影响范围内长度为λlb(λ为环缝影响长度相对系数,lb为螺栓长度),环缝影响范围外取管片纵向实际刚度,环缝影响范围内取等效刚度,环缝影响范围内、外两部分为刚性连接。下面推导环缝影响范围内纵向等效轴向、弯曲和剪切刚度。
1.1 基本假定
管片纵向均质等效模型中,管片横截面均采用连续均质模型,管片环缝接头处的变形符合平截面假定,且为了便于计算,认为环缝接头处螺栓沿环缝截面均匀分布。本文在对管片纵向进行非均质化等效时依然采用这些假定,并根据非均质等效连续模型的特点,作如下基本假定:
(1) 横截面符合平截面假定,且环缝影响范围外中性轴在形心位置,环缝影响范围内中性轴位置沿纵向保持不变;
(2) 螺栓刚度和传力衬垫在环缝处连续均匀分布;
(3) 环缝影响范围内受压侧变形由管片承担,受拉侧变形根据环缝影响长度考虑为拉力由螺栓或螺栓和管片共同承担两种情况;
(4) 环缝影响外取管片实际刚度;
(5) 螺栓形成的圆环半径与管片半径一致;
(6) 环缝影响范围外与影响范围内为刚性连接;
(7) 环缝剪切刚度首先由相邻管片摩阻力提供,当相对滑移逐渐增大到螺栓与螺栓孔相互接触时螺栓参与抗剪,不考虑榫槽提供的咬合力。
1.2 环缝影响范围内等效轴向刚度
环缝处的压缩变形主要为混凝土压缩变形。压应变由混凝土承担,等效压缩刚度可取为管片横截面的实际压缩刚度。依据基本假定,可在环缝处全截面均匀受拉下推导等效拉伸刚度,计算简图如图2所示。
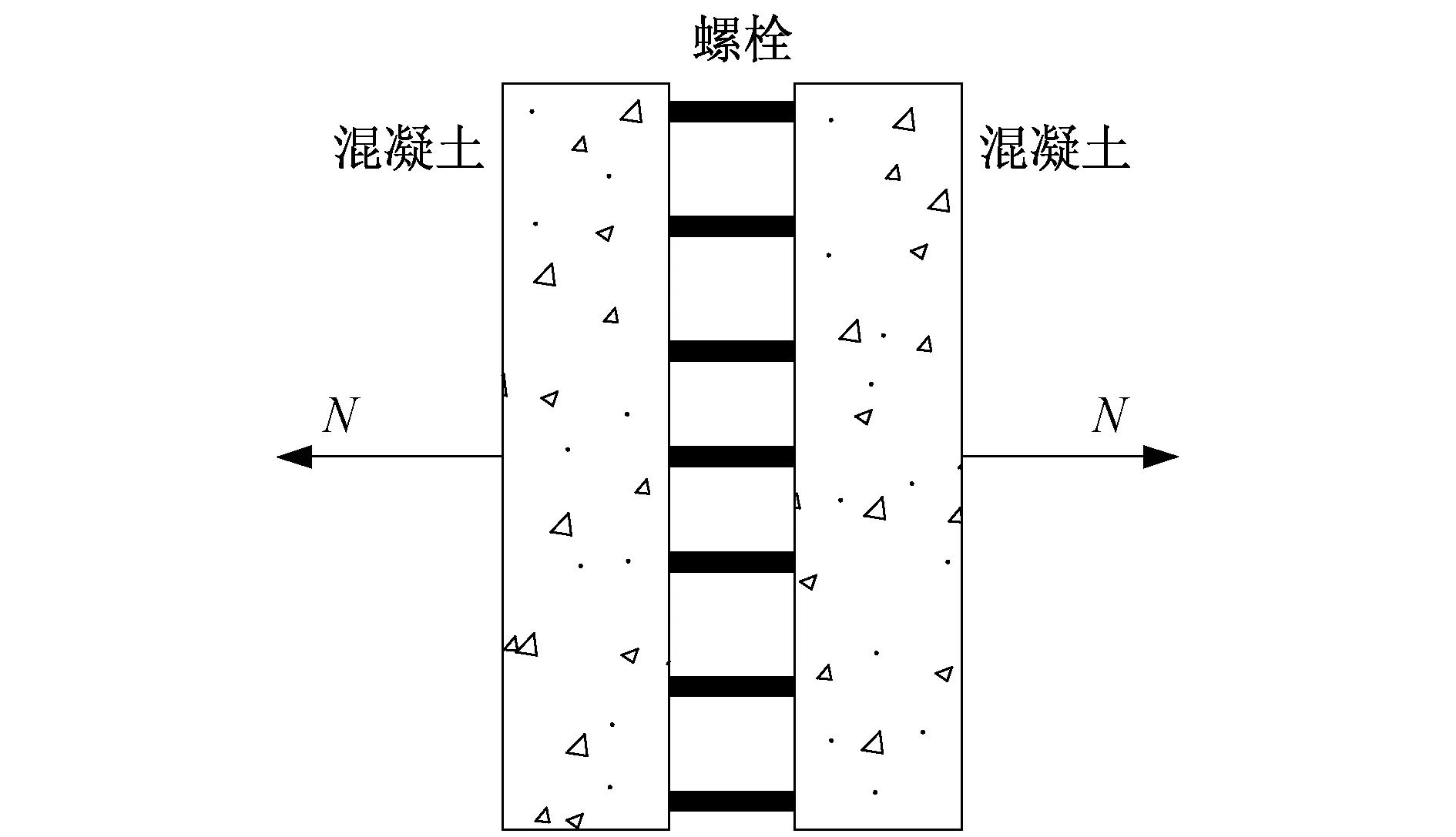
图2 等效拉伸刚度计算示意图
(1) 当λ≤1时,环缝影响范围内的混凝土部分不会产生拉伸变形,拉应变主要由螺栓承担,则等效拉伸刚度可取为螺栓的总刚度。
(2) 当λ>1时,环缝影响范围大于螺栓长度,则螺栓范围以外的部分混凝土也会产生拉应变,环缝影响范围内受外力后变形量为:
(1)
环缝影响范围内等效变形量为:
(2)
当δ=δeq时可得等效拉伸刚度:
(3)
式中:
EAeq,t——等效拉伸刚度;
lb——螺栓长度;
Ec,t——混凝土抗拉弹性模量;
Ac——管片截面面积;
Kb——环缝处螺栓总刚度,Kb=nKbi=nEbAb,其中Kbi为单个螺栓刚度,Eb和Ab分别为螺栓弹性模量和单个螺栓横截面面积,n为螺栓个数。
1.3 环缝影响范围内等效弯曲刚度
环缝影响范围内,截面中性轴位置偏离形心位置,当螺栓和管片均处于弹性应力状态时,由于管片接头处实际为不连续,所以中性轴的位置应向受压侧偏移。截面应力应变分布形式如图3。
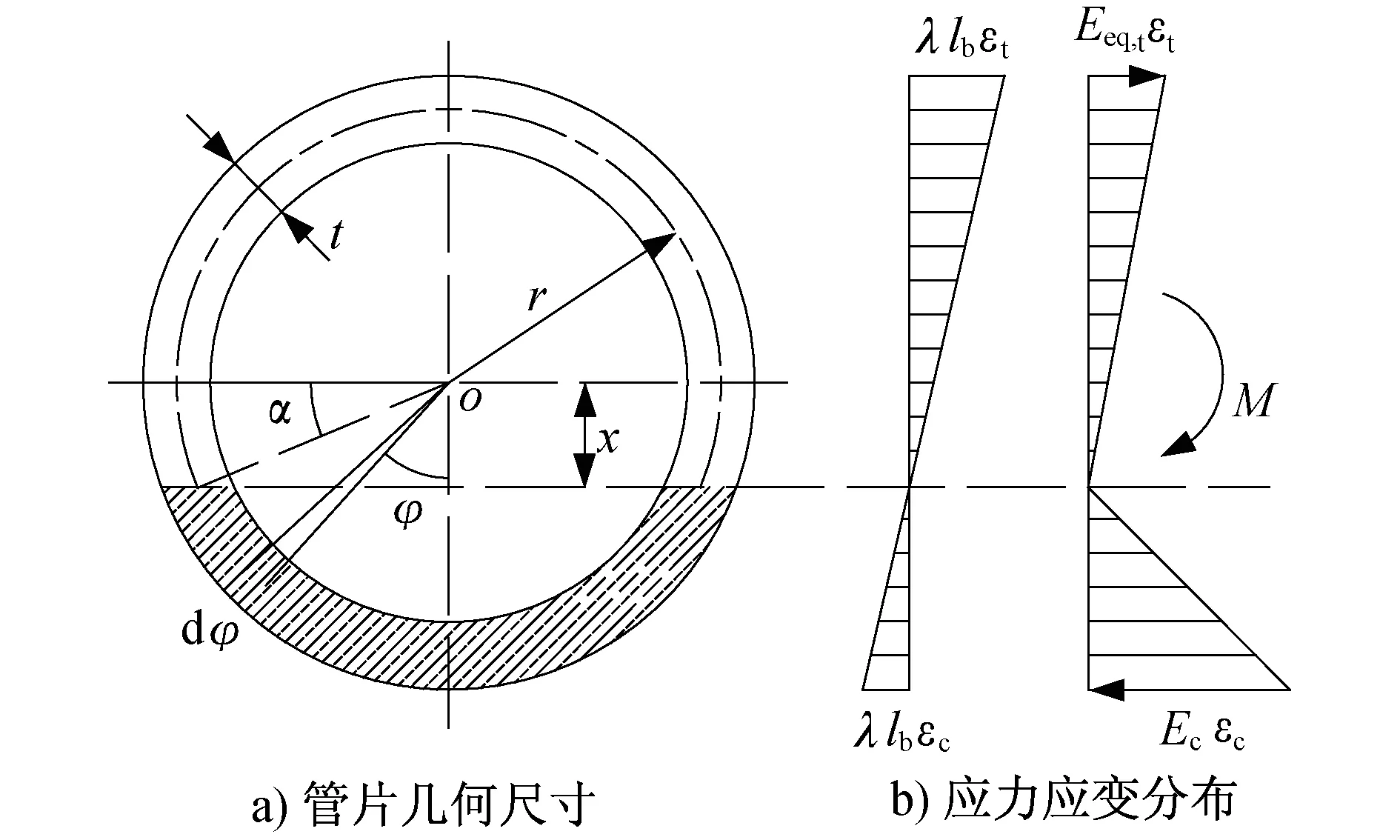
注:εc为轴向刚度等效后受压区的轴向应变;
其力的平衡方程为:
变形协调方程为:
λlbεt=(r+x)θ
(6)
λlbεc=(r-x)θ
(7)
式中:
εt——轴向刚度等效后受拉区的轴向应变;
θ——环缝影响范围内截面转角。
由式(4)~(7)可得中性轴的位置所对应的角度α(见图3)和θ为:
(8)
(9)
则环缝影响范围内纵向弯曲刚度系数为:
(10)
环缝影响范围内等效弯曲刚度为:
(11)
由等效弯曲刚度可得环缝处受拉侧张开量为:
(12)
式中:
Eeq,t——环缝影响范围内等效拉伸弹性模量,可由EAeq,t/Ac求得;
EcIc——管片实际抗弯刚度。
1.4 环缝影响范围内等效剪切刚度
当环缝处剪力较小时,相邻管片间相对滑移量较小,螺栓孔与螺栓未接触,剪力由管片接触面的滑动摩阻力承担,螺栓不参与抗剪作用;当剪力持续增大,使得相邻管片滑移量不断增大直至螺栓孔与螺栓接触,此时由于螺栓参与抗剪使得抗剪刚度突增[14-15]。实际上环缝影响范围内受拉区张开不产生摩擦力,受压区管片接触产生摩阻力,由管片接触面刚度的定义[16]和环缝接头受力特性,环缝影响范围内等效剪切刚度可表达为:
(13)
其中Kf=k(N)
(14)
式中:
Kbs——螺栓总抗剪刚度[17],Kbs=nGbAb,其中Gb为螺栓所用钢材的剪切模量;
Kf——环缝接头处接触面滑动摩阻力所提供的刚度,受管片接触面压力和剪切力共同决定;
Smax——螺栓不参与抗剪的最大容许位移值,即为螺栓直径与螺栓孔半径的差值(假设管片拼装无公差);
N——管片接触面压力。
k(N)可由荷载-位移试验得到。N由下式得出:
(15)
式中:
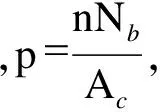
需要说明的是,隧道在运营阶段并没有明确的沿隧道纵向的作用力,所以在环缝处的接触力主要由螺栓预紧力与纵断面弯矩产生。
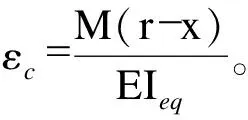
(16)
2 实例计算与对比分析
志波由纪夫及川岛一彦的等效均质模型(志氏模型)采用管段全长抗弯刚度均与环缝处相等,其等效抗弯刚度计算式见式(17)[18]。文献[6]提出的等效均质模型(徐氏模型)考虑了管段与环缝处刚度的不同,通过环缝变形量等效的方法来计算管段全长的等效抗弯刚度,见式(18):
(17)
(18)
式中:
l——管片宽度。
本节主要比较志氏模型、徐氏模型与纵向等效连续非均质模型在计算管片纵向弯曲性能时的差异,并计算纵向等效连续非均质模型下环缝剪切位移值。计算采用的隧道管片衬砌主要结构参数如表1所示。
上海轨道交通实测显示,管片衬砌纵向沉降呈高斯分布,隧道底部产生的反力也呈高斯分布[5,7],本文在计算时可取一定长度的隧道,假设两端固定,在隧道中部受一集中力的作用,此时隧道纵向变形基本符合高斯分布。计算模型纵向取50 m,跨中集中力大小为200 kN。徐氏模型和连续非均质模型由于均考虑了环缝影响范围,所以取λ分别为0.6、1.0和1.4时进行计算。计算结果见表2。表中等效连续非均质模型计算所得中性轴位置和等效弯曲刚度均为环缝影响范围内的计算结果,为比较环缝张开量计算结果,志氏模型环缝张开量为与环缝影响长度相同长度下的变形量。

表1 管片衬砌结构参数
志氏模型在计算等效拉伸刚度时,整个管段都计入螺栓的抗拉作用,而徐氏模型和等效连续非均质模型只在有限范围考虑螺栓的拉伸作用,所以志氏模型所计算出的中性轴位置对应角度最小(即中性轴偏离截面形心的距离最小)。志氏模型认为接头处刚度与管段相同,而徐氏模型分别计算管段刚度和环缝影响内刚度再进行等效刚度计算,所以志氏模型弯曲刚度计算结果仍比徐氏模型小。而表2中等效连续非均质模型弯曲刚度为环缝影响范围内弯曲刚度,其计算值最小符合实际情况。表2中等效连续非均质模型计算所得环缝张开量最大,这也是由于环缝影响范围内弯曲刚度小所致,而志氏模型和徐氏模型计算所得结果为任意位置处的张开量,显然这样的计算方法难以模拟真实情况。
3 环缝影响长度对各等效刚度的影响
文献[6]以上海轨道交通隧道为原型进行了纵向相似结构模型试验,分析得出上海轨道交通盾构隧道的λ=0.5,而目前λ的取值主要依靠试验和经验确定。
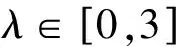
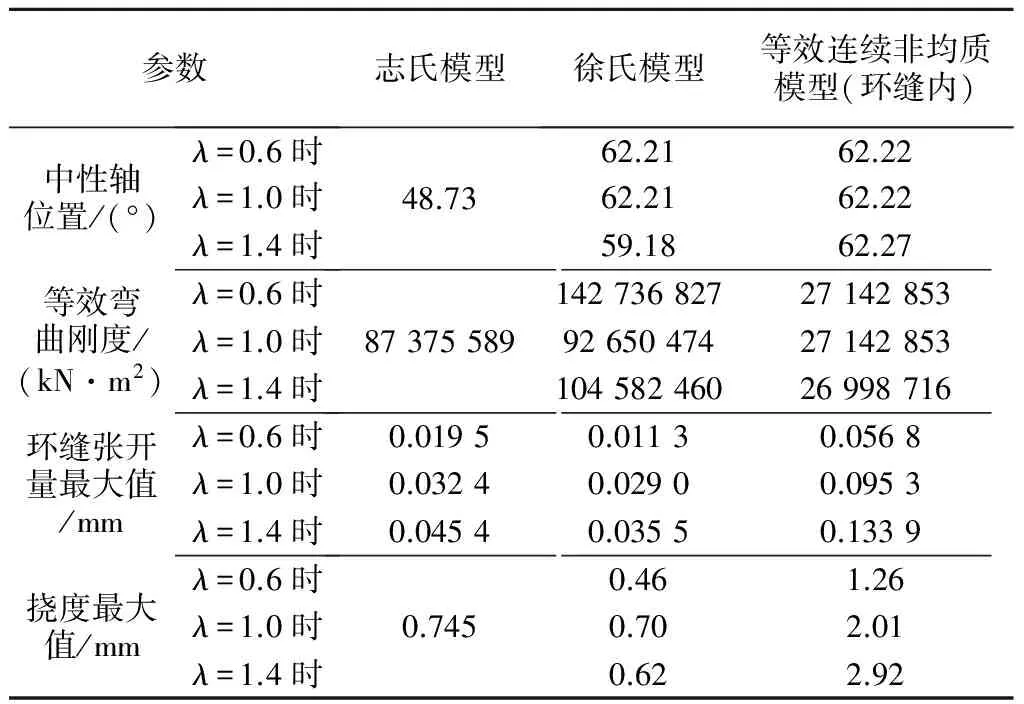
表2 三种不同模型计算结果
3.1 环缝影响长度对等效轴向刚度的影响
图4为等效拉伸刚度与环缝影响长度的关系,可以看出,λ≤1时等效拉伸刚度不受环缝影响长度的影响,λ>1时等效拉伸刚度随λ的增大而减小。
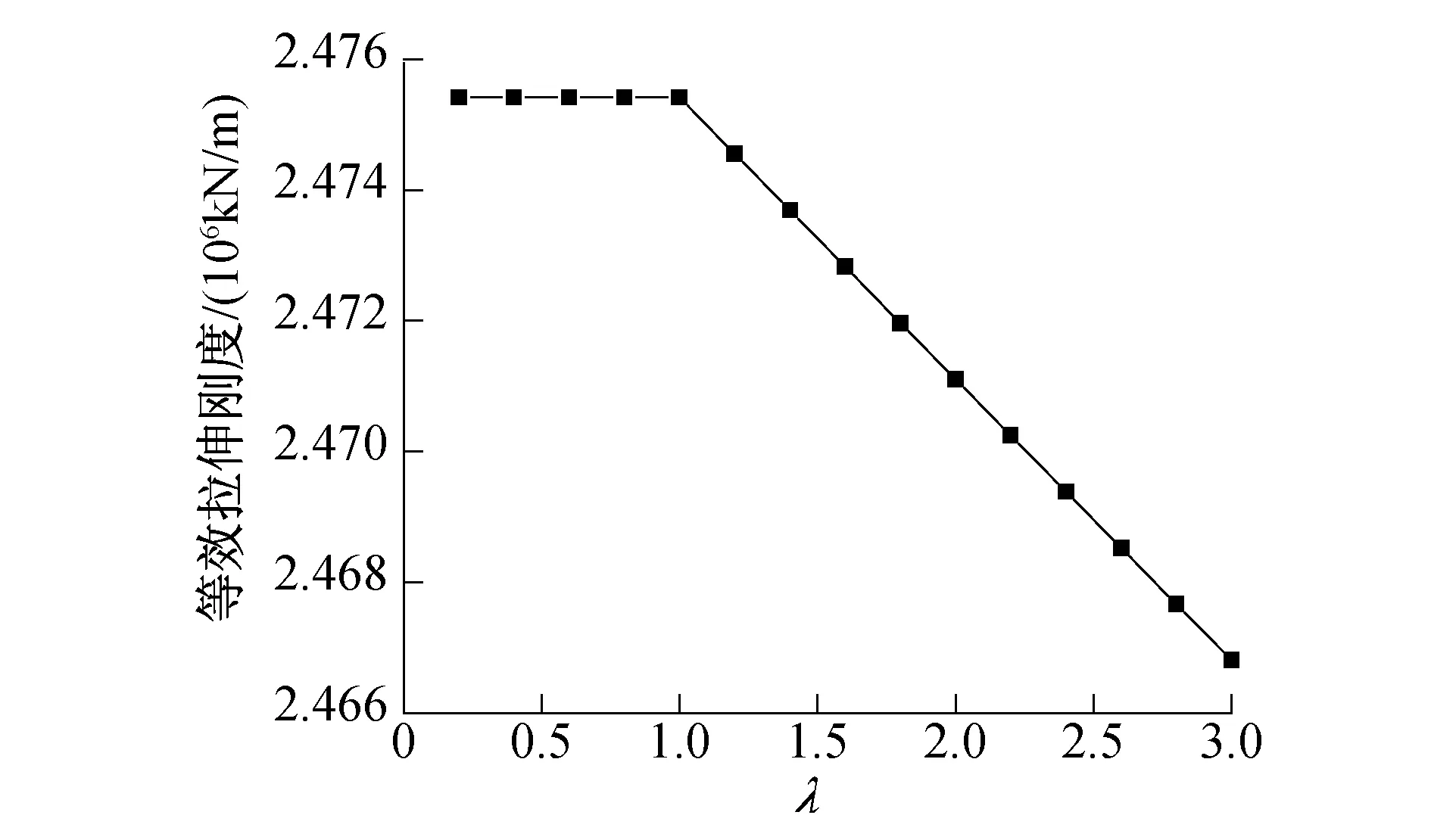
图4 环缝影响长度与等效拉伸刚度关系曲线
3.2 环缝影响长度对等效弯曲刚度的影响
环缝影响长度首先影响等效拉伸刚度,显然中性轴的位置(α)与压缩刚度和拉伸刚度的比值有关,所以中性轴的位置必然随着环缝影响长度的改变而改变。图5为环缝影响长度与中性轴位置关系曲线。从图5中可以看出,中性轴位置(α)随环缝影响长度增大而增大,即中性轴有往截面形心移动的趋势。图6和图7分别为等效弯曲刚度有效率和等效弯曲刚度与环缝影响长度的关系曲线,可以看出,等效弯曲刚度随着环缝影响长度的增加而减小。
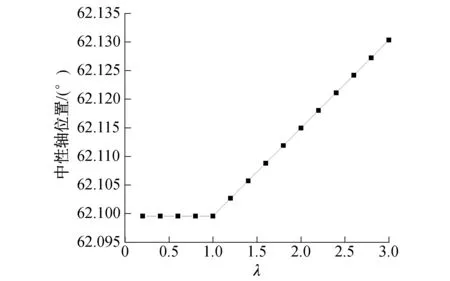
图5 环缝影响长度与中性轴位置关系曲线

图6 环缝影响长度与等效弯曲刚度有效率关系曲线

图7 环缝影响长度与等效弯曲刚度关系曲线
图8为在不同弯矩作用下环缝张开量与环缝影响长度关系曲线,可见,环缝张开量随着弯矩和环缝影响长度的增大而增大。
3.3 环缝影响长度对等效剪切刚度的影响
环缝影响长度会影响中性轴的位置,从而对环缝处受压区面积和压应力分布产生影响。另一方面,由式(18)可知,不同弯矩作用下环缝受压区压应力也不同,使得相邻管片接触面所受摩擦力不同。所以,等效剪切刚度受上述两个因素综合影响。
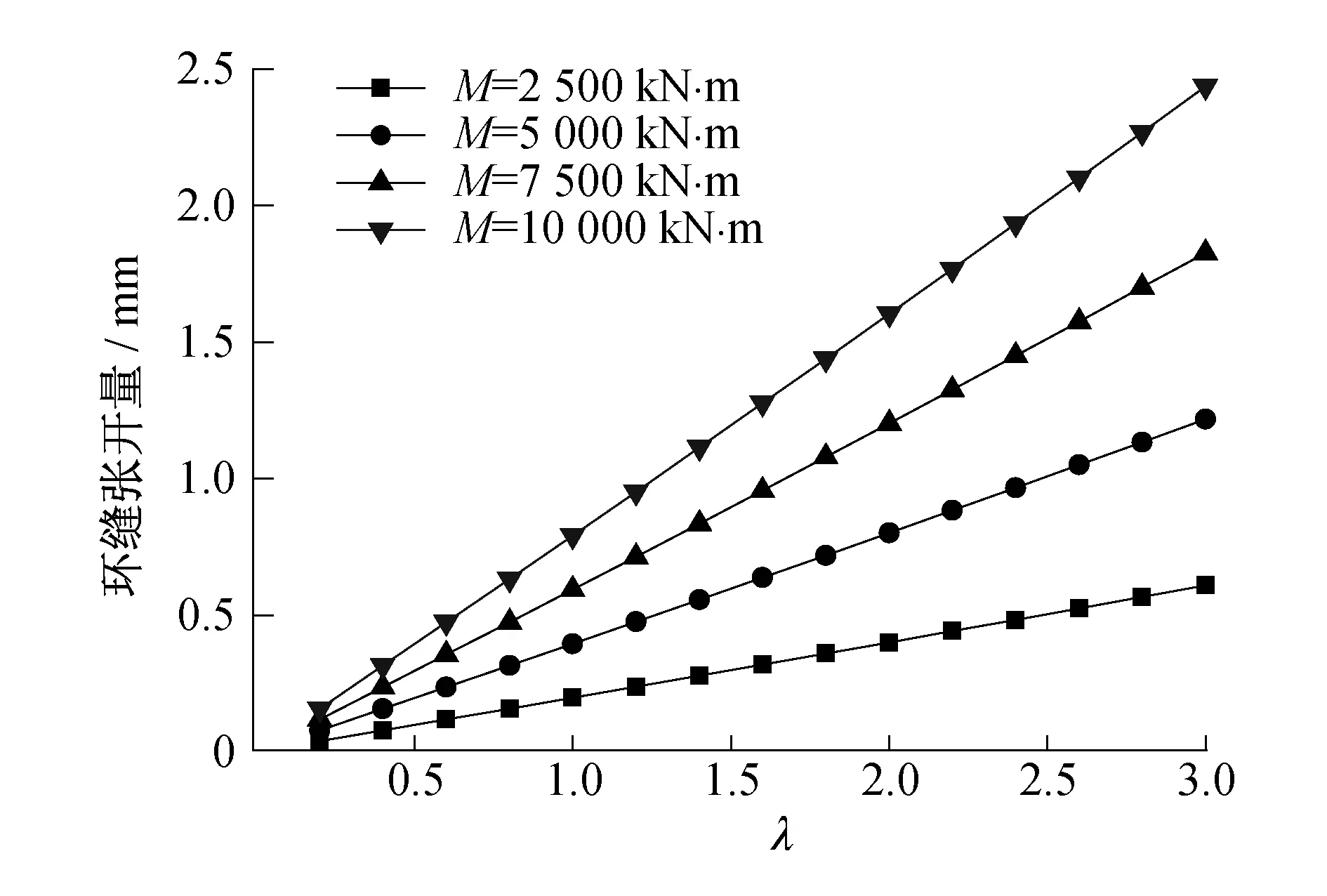
图8 不同弯矩作用下环缝影响长度与环缝张开量关系曲线
4 结语
本文提出管片纵向等效连续非均质模型,将隧道沿纵向分为环缝影响范围内、外两部分。通过计算实例,对该模型与纵向等效连续均质模型进行计算与对比分析,并探讨环缝影响长度对各等效刚度的影响,得到以下结论:
(1) 等效拉伸刚度在环缝影响范围内由螺栓和管片承担,压缩刚度则完全由管片混凝土提供,计算所得等效拉伸刚度小于压缩刚度,当λ≤1时等效拉伸刚度不随λ的改变而改变,当λ>1时等效拉伸刚度随λ的增大而减小。
(2) 拉伸刚度小于压缩刚度导致环缝影响范围内中性轴位置向压缩一侧发生偏离,当λ≤1时,中性轴位置不随λ改变而变化,从而等效弯曲刚度不随λ变化而变化;当λ>1时,等效拉伸刚度随λ增大而减小,中性轴位置进一步向截面受压一侧偏移,等效弯曲刚度减小,环缝张开量随λ增大而增大。
(3) 剪切刚度首先由相邻管片间的摩阻力提供,当剪切位移发展到螺栓与螺栓孔接触时,螺栓参与抗剪作用。λ对等效剪切刚度影响不显著。
(4) 纵向等效连续非均质模型在环缝影响范围内中性轴位置更靠近受压一侧,从而弯曲刚度最小,环缝张开量最大。
[1] TALMON A M,BEZUIJEN A.Analytical model for the beam action of a tunnel lining during construction[J].International Journal for Numerical and Analytical Methods in Geomechanics,2013,37(2):181-200.
[2] MO H H,CHEN J S.Study on inner force and dislocation of segments caused by shield machine attitude[J].Tunnelling and Underground Space Technology,2008,23(3):281-291.
[3] 余占奎,黄宏伟,徐凌,等.软土盾构隧道纵向设计综述[J].地下空间与工程学报,2005,1(2):315-318.
[4] WANG Z,WANG L,LI L,et al.Failure mechanism of tunnel lining joints and bolts with uneven longitudinal ground settlement[J].Tunnelling and Underground Space Technology,2014,40(1):300-308.
[5] SHEN S,WU H,CUI Y,et al.Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai[J].Tunnelling and Underground Space Technology,2014,40(12):309-323.
[6] 徐凌.软土盾构隧道纵向沉降研究[D].上海:同济大学,2005.
[7] 樊振宇.软土盾构隧道衬砌结构计算方法及纵向变形分析[D].上海:同济大学,2009.
[8] 叶飞,何川,朱合华,等.考虑横向性能的盾构隧道纵向等效刚度分析[J].岩土工程学报,2011,33(12):1870-1876.
[9] 张文杰,徐旭,李向红,等.广义的盾构隧道纵向等效连续化模型研究[J].岩石力学与工程学报,2009,28(A02):3938-3944.
[10] 廖少明,侯学渊,彭芳乐.隧道纵向剪切传递效应及其一维解析[J].岩石力学与工程学报,2005,24(7):1110-1116.
[11] LIAO S,PENG F,SHEN S.Analysis of shearing effect on tunnel induced by load transfer along longitudinal direction[J].Tunnelling and Underground Space Technology,2008,23(4):421-430.
[12] TALMON A M,BEZUIJEN A.Calculation of longitudinal bending moment and shear force for Shanghai Yangtze River Tunnel:Application of lessons from Dutch research[J].Tunnelling and Underground Space Technology,2013,35(3):161-171.
[13] 王湛.软土地层中盾构隧道结构沉降与变形机制分析[D].杭州:浙江大学,2013.
[14] 黄钟晖,廖少明,侯学渊.错缝拼装衬砌纵向螺栓剪切模型的研究[J].岩石力学与工程学报,2004,23(6):952-958.
[15] 奚程磊.盾构法隧道管片接头形式研究及其优化[D].上海:同济大学,2006.
[16] 艾辉军,彭立敏,施成华.基于三维非连续接触模型的管片接头静动力特性分析[J].岩土工程学报,2013,35(11):2023-2029.
[17] 周海鹰.盾构隧道衬砌管片结构的力学性能试验及理论研究[D].大连:大连理工大学,2011.
[18] 郑永来,韩文星,童琪华,等.软土地铁隧道纵向不均匀沉降导致的管片接头环缝开裂研究[J].岩石力学与工程学报,2005,24(24):4552-4558.
Longitudinal Heterogeneous Equivalent Continuous Model for Stagger Joint Segmental Lining
GUO Le, YANG Xin′an, QIU Yan
Segmental lining is divided into two parts in and out of the influence range of circumferential joint along longitudinal direction,the stiffness of segmental lining in this influence range is the actual value,but it is the equivalent value when out of the influence range of circumferential joint,the coupling in and out of the influence range is regarded as rigid coupling.By using analytical method,the equivalent axial and bend stiffness in the influence range of circumferential joint are deduced,the longitudinal heterogeneous equivalent continuous model is compared with the homogeneous equivalent model. On this basis,the concept of equivalent shear stiffness is put forward,which holds that the shear stiffness is carried by frictional resistance firstly with the evolution of shear displacement,the bolt will carry part of the shear stiffness when bolt touches with bolt hole.Thus the calculation formulas of equivalent shear stiffness and shear displacement are deduced, and the relationship between the influence range of circumferential joint and equivalent stiffness is illustrated.
shield frame; segmental lining; longitudinal continuous model; heterogeneous; influence range of circumferential joint; equivalent stiffness
U451+.4
10.16037/j.1007-869x.2017.04.004
2015-05-20)

