环状直流配电网故障测距方法

谢俊州，吕飞鹏，林婵娟

（1.四川大学电气工程学院，成都 610065；2.国网凉山供电公司电力调度控制中心，西昌 615000）

随着电力电子技术的不断发展，直流配电网在传输容量、经济运行及电能质量等方面的优势逐渐显现[1-2]，其中基于电压源换流器的环状直流配电网具有控制灵活、可靠性高、线路损耗小、便于接纳分布式电源等优点，具有较好的应用前景[3-4]。当直流配电线路发生故障后，从电力系统安全性和可靠性角度出发，必须快速找到故障位置。因此，研究线路的故障测距技术对直流配电网的可靠运行具有重要意义。

目前，国内外针对高压直流输电的故障测距方法研究较多[5-8]，但由于直流配电网具有结构多样、线路短等特点，应用于高压长距离输电的故障测距方法不再适用于直流配电网，因此有必要对直流配电线路的故障测距方法进行研究。故障测距方法主要分为行波法、暂态法和注入法。文献[9-10]利用了行波在波阻抗不连续节点的反射特性来计算故障距离，该方法原理简单，但由于直流配电线路较短，为准确扑捉第一个行波波头，需要较高的采样频率，对硬件要求较高，同时在接地电阻过高的情况下，行波波头幅值不明显，影响测距精度。文献[11]利用电容放电阶段的暂态电流、电压信息建立故障测距公式，该方法消除了过渡电阻的影响，测距精度较高。文献[12]利用单端量信息实现故障定位，但文中建立的故障测距模型未考虑对侧故障电流在过渡电阻上的压降，测距结果极易受过渡电阻的影响。文献[13]研究了注入法故障测距方法，其原理是在故障切除后通过对故障线路增加故障测距模块，构建RLC二阶电路零输入响应，并依据能量守恒原理建立故障测距算法，该方法消除了过渡电阻影响，测距精度高，但操作较复杂。文献[14]根据故障后RLC谐振阶段的暂态放电信息，并利用故障点两侧电流谐波量实现故障定位，该方法对两端信息的同步性要求较低。目前，针对环状直流配电网故障测距方法研究较少，文献[15]采用主动控制后电压源换流器VSC（voltage source converter）直流侧输出电压的周期性与电力电子元件的可控性，构建电压源换流器与故障点的唯一回路，实现单端故障定位，该方法原理简单可靠，但整个故障隔离时间较长。

本文对环状直流配电网故障测距方法进行了研究。文章首先分析了直流配电网故障初期的暂态特性，并利用其特点，在故障点两侧建立时域微分方程，联立方程求解得到故障距离。然后分析了数值法求电流导数的方法，在此基础上，提出了一种降低测距误差率的采样点选取方法，经过仿真验证，该方法在一般采样频率下，测距精度较高，且在经过不同过渡电阻短路时都具有良好的精度。

1 短路故障分析

本文以如图1所示的四端环状直流配电网为研究对象，VSC1、VSC2、VSC3、VSC4都是基于电压源换流器的两电平换流站。

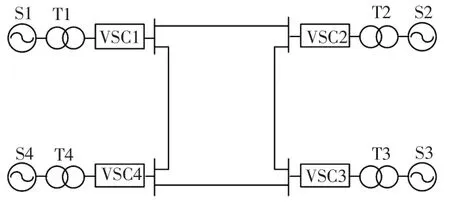
图1 环状直流配电网示意Fig.1 Schematic of ring DC distribution network

1.1 单端直流系统故障特性

直流线路故障分极间短路故障和单极接地故障，文献[16-17]根据故障过程，将直流线路故障分为不同阶段，其中发生极间短路故障、极间电压大于交流侧任一线电压，或发生单极接地故障、故障极电压大于交流侧任一相电压时，故障过程为直流电容放电阶段，该阶段的故障电流由电容放电电流和交流侧电感续流共同提供，由于交流侧电感续流较小，可以忽略，所以在这一阶段故障电流主要以电容放电电流为主[17]，其等效电路模型如图2所示，图中C、L、R分别为放电回路的等效电容、电感和电阻。

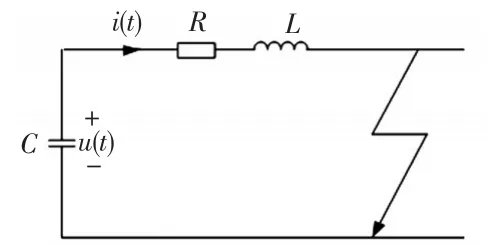
图2 直流电容放电等效模型Fig.2 Equivalent model of DC capacitor discharge

根据图2列写等效电路的KVL方程为

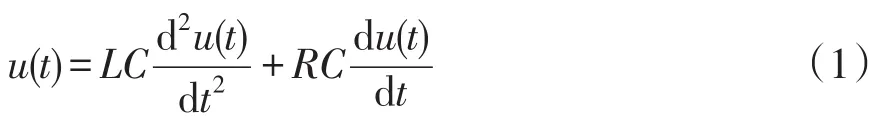
式中，u（t）为电容电压。设电容电压和电感电流的初始值分别为u（0）和i（0），则微分方程的解如下。

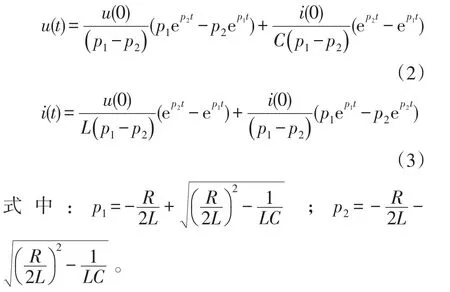
1.2 环状直流配电网故障特性

单端直流系统发生故障时，放电回路单一，故障初期的暂态过程求解如1.1节所述，而环状直流配电网任意一条线路发生故障，各个换流站均会向故障点馈入短路电流，故障过程复杂。同单端直流系统一样，环状直流配电网线路发生故障后，故障初期也为电容放电阶段[18-19]，其暂态电流主要以电容放电电流为主，且流向故障点的电流由各个换流站直流单元共同提供。以图1中VSC1与VSC2之间直流线路发生正极接地故障为例，得到如图3所示的电容放电等效电路。图中C表示故障极等效电容，R和L为等效电阻和电感，Rf为过渡电阻。

根据图3，列写回路1至回路5的KVL方程和节点n1至n4的KCL方程为

图3 环状直流配电网正极接地故障直流侧等效电路Fig.3 DC-side equivalent circuit under positive grounding fault in ring DC distribution network

式中：uC(t)为故障极电容电压；iC(t)为电容放电电流；i（t）为线路电流。式（6）和（7）可整理成状态方程，并将各个变量的初始值带入方程，通过求解多元一次微分方程组便能得到各直流单元的电压和线路的电流值。

发生双极短路故障后，正、负极电容均向故障点放电，其等效电路包含了正、负极等效电容及线路的等效电阻和电感，且故障电流从正极电容的正端出发通过故障线路和故障点流入到负极电容的负端。其回路的KVL方程和节点的KCL方程列写方法同单极接地故障类似，本文不再赘述。

2 环状直流配电网故障测距原理

直流配电线路的长度基本在15 km以内，其分布电容比较小，且换流站直流侧采用大电容，远大于直流线路的分布电容，因此，直流线路发生短路故障时，可以忽略线路分布电容对故障电流的影响[11-13]。

2.1 单极接地故障测距

为方便分析，将图3简化成如图4所示的电容放电等效电路，图中段虚线为故障点两侧换流站并联电容的放电路径，点虚线为其他换流站并联电容对故障点的放电路径。设直流线路的总长度为m（km），每km线路电感为l，电阻为r，故障发生在距左侧直流母线x处。

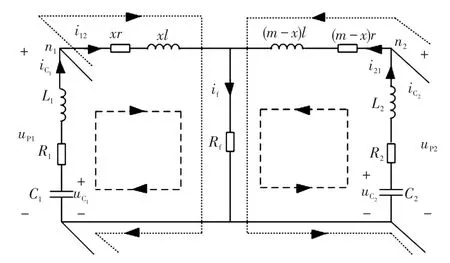
图4 单极接地故障直流侧等效电路Fig.4 DC-side equivalent circuit under single-pole grounding fault

根据基尔霍夫电压定律，可得到左右两边回路的KVL方程为

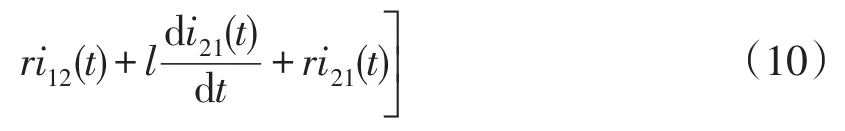
设故障极直流母线对地电压分别为uP1(t)和uP2(t)，根据图4可列写故障极电容的正端至母线n1(n2)间的KVL方程为

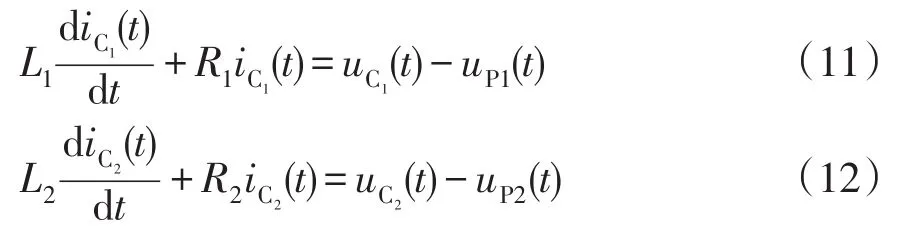
将式（11）和（12）代入式（10）得

2.2 双极短路故障测距

双极短路故障时，正、负极电容通过故障线路向故障点提供短路电流，其简化的电容放电等效电路如图5所示。图中CF1和CF2分别为故障点两侧极间等效电容，其余参数同单极接地故障中的参数含义相同。

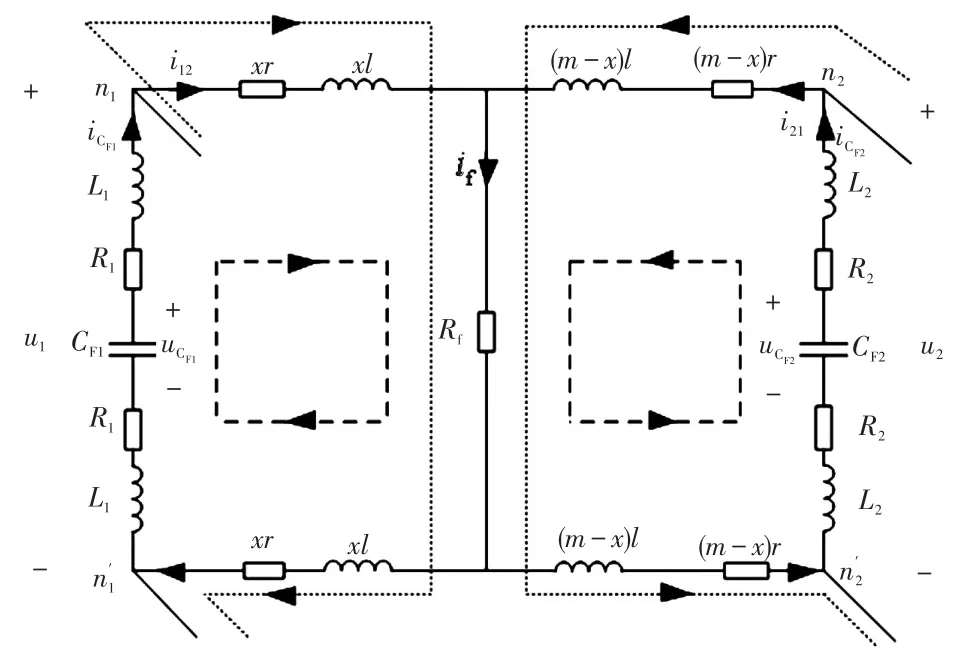
图5 双极短路故障直流侧等效电路Fig.5 DC-side equivalent circuit under bipolar short-circuit fault

根据图5同样可得左右两边回路的KVL方程为

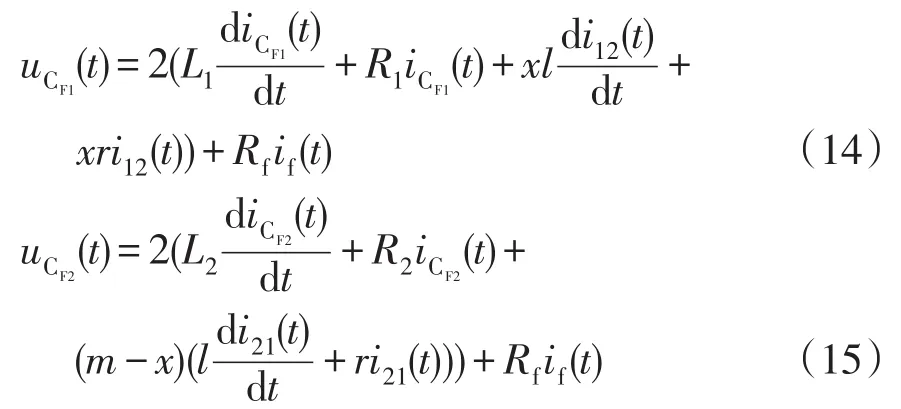
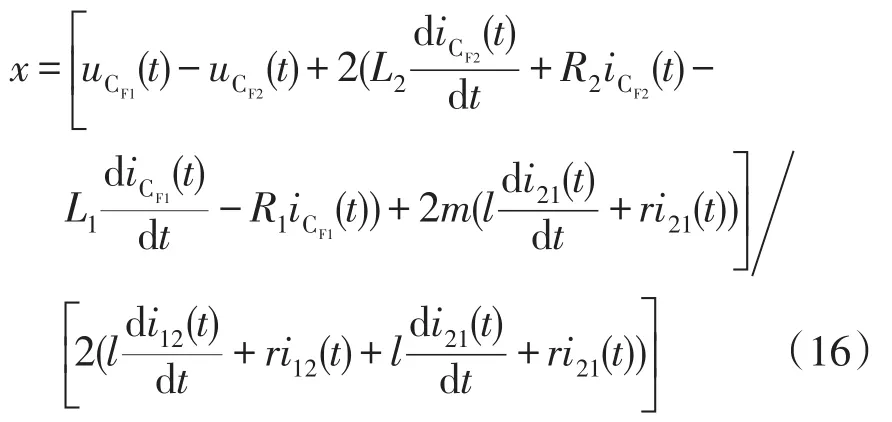
设直流母线极间电压分别为u1(t)和u2(t)，根据图5列写等效电容和直流母线间的KVL方程为

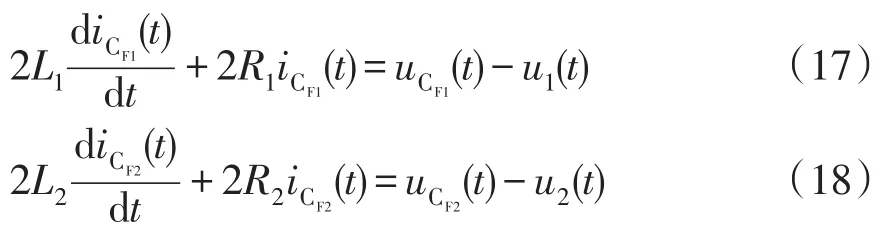
将式（17）和（18）代入式（16）得

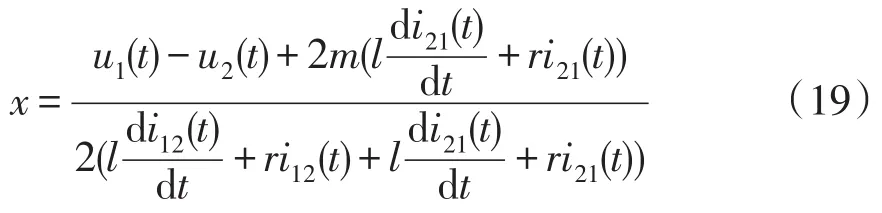
由式（13）和（19）可以看出，在环状直流配电网发生故障后，可直接利用故障点两侧直流母线电压和故障线路的电流信息联立计算得到故障位置，并且故障测距结果不受过渡电阻的影响。

本文所提的故障测距方法是利用故障点两侧的暂态信息实现故障定位，所以必须要保证两侧数据同步。目前电力系统使用的GPS对时系统能将时间误差控制在10 μs内，因此，在选取合适的采样频率下，可以实现两端信息的完全同步。实际应用时，首先对故障点进行隔离，然后提取两侧的故障录波数据。由于该方法使用的是电容放电阶段的暂态信息，计算前必须对故障录波数据进行分析，选取故障起始时刻至电容电压大于交流侧电压时段内的数据进行故障测距计算。

2.3 电流微分计算

在式（13）和式（19）中，故障测距需要计算电流微分，而实际电流数据是经过采样后得到一系列的离散信号，所以工程上一般采用数值方法计算微分，下面介绍两种数值方法计算在x1点的微分。

1）差分法

由于系统是等节点采样，有x1-x0=x2-x1=h，则得到向前差分和向后差分的算式为

截断误差为

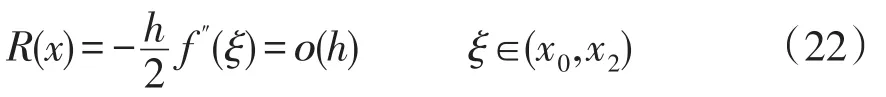
2）二次插值法

设已知三点 (x0,f(x0))、(x1,f(x1))、(x2,f(x2))，在三点做二次插值得到的方程为

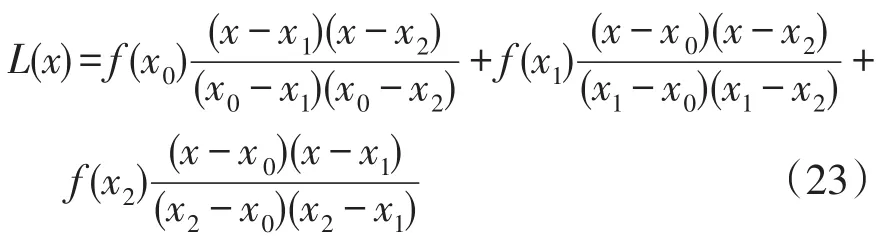
对L（x）求导得

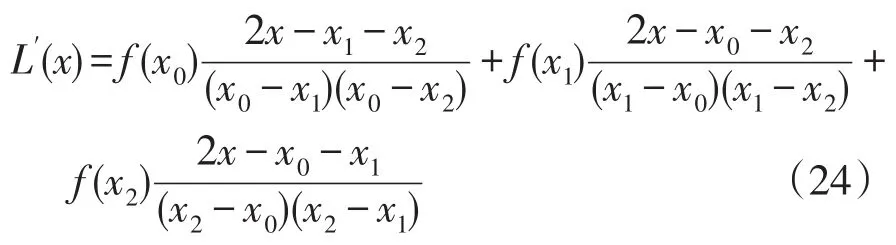
则在x1的导数值及截断误差分别为

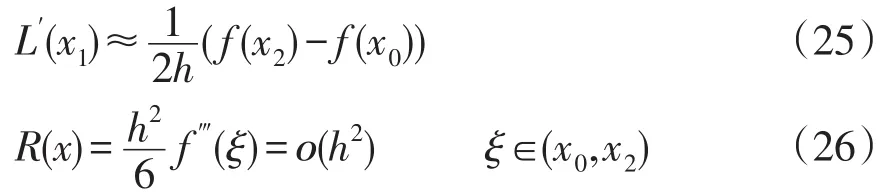
由式（22）和（26）可知，在相同步长下，相对于差分代替微分的误差阶ο(h)，插值法求微分的误差阶提高到ο(h2)，因此，本文采用二次插法计算电流微分。

3 仿真验证

3.1 仿真参数

本文在PSCAD/EMTDC仿真平台上搭建如图1所示的四端环状直流配电网，并在VSC1与VSC2线路之间进行故障仿真验证，具体仿真参数如表1所示。

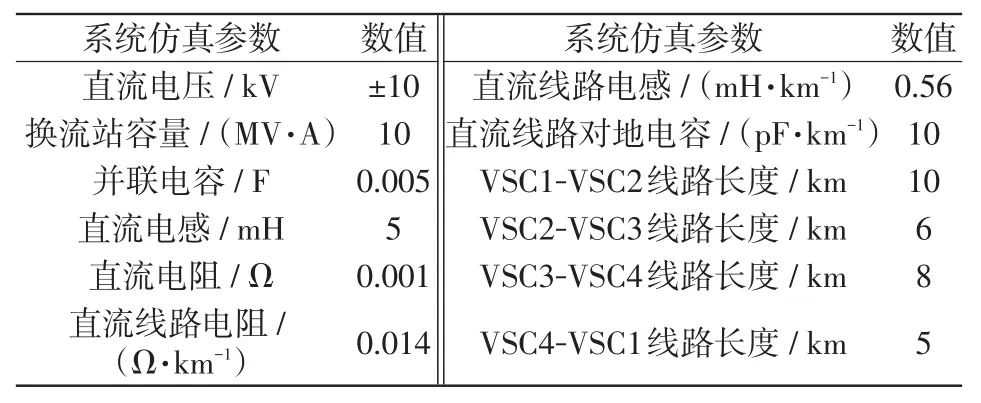
表1 仿真参数Tab.1 Simulation parameters

3.2 采样频率

本文利用GPS对时系统实现双端信息同步，为保证两端采样数据的同步，采样步长应小于或等于GPS对时系统的精度，因此，采样频率应满足f≤100 kHz。与此同时，电容放电周期约为几ms，为保证放电周期内有足够的点参与下文的故障测距计算，采样频率应满足f≥20 kHz。由式（26）可以看出，采样频率越高，步长越小，误差R（x）越小，但步长过小，会造成舍入误差增大，同时，采样频率越高，对故障录波装置的硬件要求越高。因此，从舍入误差和经济性方面考虑，采样频率不宜太高。综上所述，本文设置的采样频率f=20 kHz。

3.3 低误差率采样点选取方法

故障测距误差率为

在距VSC1直流母线1km分别设置大小为0.1Ω、10 Ω、50 Ω的过渡电阻进行正极接地故障仿真，提取故障后10 ms录波数据导入Matlab中，并利用式（13）和（27）计算每一个采样点的测距结果及其误差率，得到按时间顺序排列的误差率，结果如图6所示。

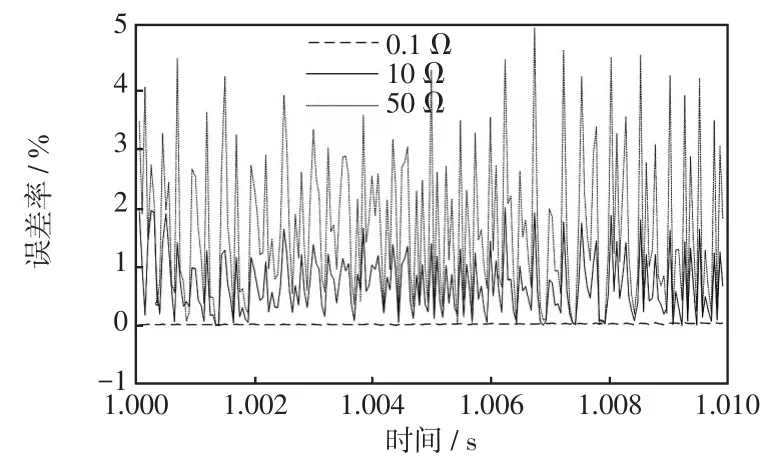
图6 时间顺序排列的误差率Fig.6 Error rate of time-sequence arrangement

由图中可以看出，在经小电阻接地时，误差率波动较小，在经大电阻接地时，误差率时高时低，且过渡电阻越大，误差率波动越大。因此若直接选取采样窗内任意一个点的计算值作为故障测距结果，将难以保证测距精度。由式（13）和（19）可知，在保证线路参数准确的情况下，误差率主要受电流微分的影响。

根据式（26）得，当步长一定时，R（x）的值与f‴(ξ)的范围也相关，几何上三阶导数反映了曲线在单位区间内的弯曲程度，当 f‴(ξ)较小时，曲线弯曲度较小，当 f‴(ξ)越大时，曲线越弯曲。其几何意义分析如下：电容放电过程的电流曲线是非线性函数，可用f（x）表示，如图7所示，f′(x1)和L′(x1)分别为函数f（x）在点x1的实际微分和二次插值计算的微分，由图中可以看出，在(x0,x2)区间内，函数f（x）越线性，则二次插值法计算的微分与实际值越接近。因此，当x1-x0=x2-x1时，(f(x2)-f(x1))-(f(x1)-f(x0))的值越小，采用二次插值法计算的微分误差越小。

图7 电流微分示意Fig.7 Schematic of current differential

因此通过点x0、x1、x2的电流曲线弯曲程度可以表示为

因为电流曲线的凹凸性会发生变化，a的极性也会随着发生变化，对式（28）两边取平方得

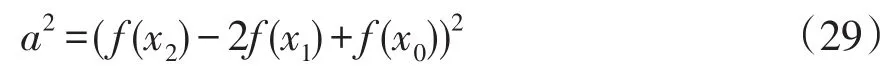
即a2的值越小，曲线的弯曲程度越小，所得的 f‴(ξ)的范围也就越小，误差R（x）的范围也就越小。下面根据前面的仿真数据对采样点选取方法进行验证。

由于VSC2侧的故障电流在式（13）和（19）中的分子和分母均参与了微分运算，为减小误差，以VSC2侧的故障电流计算a2（首尾两点不计算），并对a2由小到大进行排列，其对应的故障测距误差率如图8所示。

图8 a2由小到大排列的误差率Fig.8 Error rate ofa2arrangement in increasing order

由图中可以看出，在前20个采样点内，误差率均在1%以内，在a2较大时误差率较大，且波动程度随a2的值增大而增大。因此，通过选取a2数值较小的点所对应的电流、电压数据参与故障测距计算，得到的测距精度较高。具体步骤如下：

首先利用式（29）计算对侧电流的a2，并对a2由小到大进行排列；为提高算法稳定，选取前3个点对应的暂态电流、电压信息代入式（13）和（19）进行测距计算；最后取3个点的平均值作为故障测距结果。

3.4 单极接地故障测距

在不同的故障点设置大小为0.1 Ω、1 Ω、10 Ω、50 Ω的过渡电阻进行正极接地故障仿真，得到的结果如表2所示，测距结果表明，该方法具有较高的测距精度，即使在高过渡电阻接地情况下，误差率也小于0.5%。

表2 正极接地故障测距情况Tab.2 Location of positive grounding fault

3.5 双极短路故障测距

双极短路故障多为金属性短路，过渡电阻较小，本文在不同故障点设置大小为0.1 Ω、10 Ω的过渡电阻进行双极短路故障仿真，得到如表3所示的测距结果，分析表3的数据可知，双极短路的故障测距精度也较高，即使在线路首末端发生故障，误差率均能控制在0.1%以内。

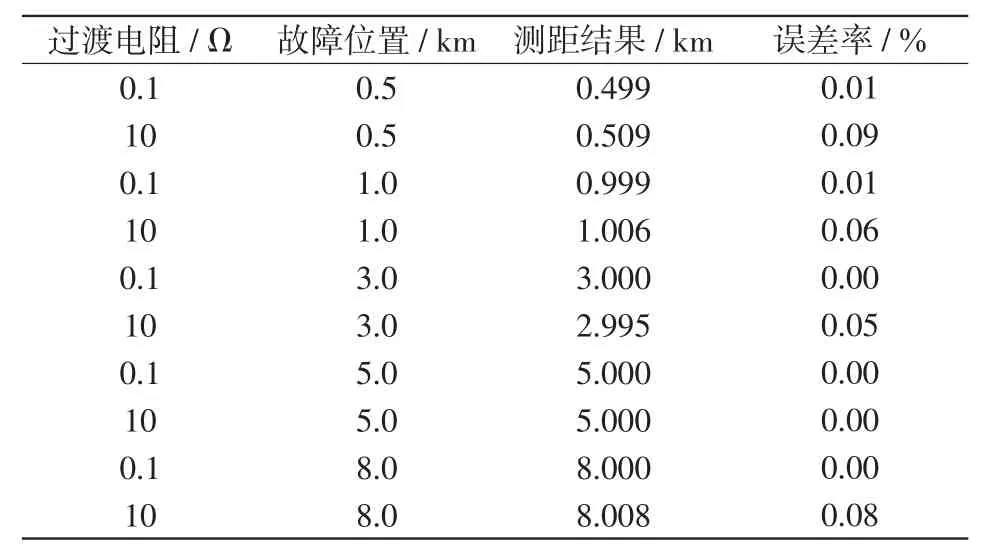
表3 双极短路故障测距情况Tab.3 Location of bipolar short-circuit fault

3.6 对比验证

本文所提的方法是将暂态法应用在环状直流配网实现故障定位，在此基础上，对数值微分法进行分析，提出了一种降低测距误差率的采样点选取方法。为了检验方法的效果，将该方法与文献[11]所提到的暂态法、行波法和注入法进行比较，结果如表4所示。

表4 不同测距方法的对比结果Tab.4 Comparison of results obtained using different location methods

由表4可以看到，4种方法得到的测距精度均较高，其中行波法和注入法的测距误差率均在2%以内，但行波法的采样频率为1 000 kHz，对硬件的要求较高。在相同采样频率下，本文所提的方法和暂态法相比，本文所提的方法测距精度更高。

4 结论

本文研究了基于电压源换流器的环状直流配电网在直流线路发生故障时的故障测距方法，分析得出以下结论：

（1）利用故障点两侧直流母线电压和故障电流信息实现了环状直流配电网的故障定位，该方法消除了过渡电阻对测距结果的影响；

（2）在电流微分计算中，利用二次插值法求微分，可以降低数值微分计算引起的误差；

（3）提出了一种降低测距误差率的采样点选取方法，利用选取的点参与故障测距计算，得到的结果精度高，且在经过不同过渡电阻短路时都具有良好的精度。