采用扰动观测器的SVG直接电流反步控制

刘玉琦，王 丹，彭周华，刘 陆，周 鑫

（大连海事大学船舶电气工程学院，大连116026）

静止无功发生器SVG（static var generator）作为无功补偿的重要设备，被广泛使用在风电系统[1]、配电系统[2]以及微电网[3]等领域。与传统的无功补偿设备，如晶闸管控制电抗器TCR（thyristor controlled reactor）以及晶闸管投切电容器TSC（thyristor switch capacitor）相比，SVG具有电流谐波分量低、响应速度快、适用范围广等优点[4-5]。通过控制PWM桥中开关器件的动作，SVG交流侧输出期望电流，进而补偿电力系统所需的无功电流。由于PWM整流桥具有四象限运行的特性，因此SVG可以实现对无功电流的动态补偿[6-7]。然而SVG的动态性能会受到系统参数不确定以及外部干扰的影响，因此研究增强SVG抗干扰能力的方法具有重要理论意义和实际应用价值。

近几年，一些先进的控制策略被应用到SVG控制器中。文献[8]将分布式最大功率跟踪控制应用到无功电流控制中，获得了较好的补偿效果；文献[9]基于广义神经网络技术估计负载的有功、无功电流值，并将估计值输入到控制器，在补偿无功功率以及抑制谐波方面取得良好的效果。通过分析上述文献的仿真结果以及实验数据可以看出，虽然这些控制方法在稳态时具有很好的无功补偿效果，但是并没有考虑干扰项对系统的影响，系统的动态性能将不可避免地受到系统参数的不确定性以及外部干扰的影响。工业系统中存在的外部干扰以及不确定性对控制系统的性能会产生较大影响。因此在控制系统设计中，抑制外部干扰以及系统不确定项具有重要意义。为了解决这一难题，研究人员提出许多估计扰动和不确定项的方法。20世纪90年代，中国科学院研究员韩京清[10]在自抗扰控制理论中针对系统不确定项提出了扩张状态观测器ESO（extended state observer），通过选取适当的非线性函数和参数，ESO可以良好地跟踪系统不确定项；文献[11]将ESO与变结构理论结合到一起，大幅度提高了静止无功补偿器的稳定性与抗扰动能力；文献[12]设计了滑模观测器对不完全可测的电力系统的状态变量进行估计，并根据估计值设计鲁棒电压控制器，该控制器较好地解决了非线性负载变化引起的电压波动问题；文献[13]利用不确定干扰估计器 UDE（uncertainty and disturbance estimator）抑制了未知的不确定项对控制效果的影响。

扰动观测器DO（disturbance observer）自1998年被提出以来[14]，在减少干扰、估计扰动项等方面得到了大量的使用[15-16]。与上述的ESO、滑膜观测器和UDE相比，DO具有原理易于理解、稳定性能好、应用范围广等优点[17]。在文献[18]中，采用了双DO估计外部扰动，实验结果表明，该方法提高了系统的跟踪效果。文献[19]在永磁同步电机的位置跟踪控制中建立了一个最小阶观测器估计负载惯性，并完成位置跟踪控制。文献[20]将扰动观测器与内膜控制器结合到一起，并应用在恒压恒频PWM逆变器的控制中，该方法降低了谐波和低频信号造成的干扰。从上述文献可以看出，DO具有较好的跟踪不确定项以及抑制扰动的能力。

为此，本文采用一种基于DO的反步控制方法以降低扰动的影响，并增强系统的动态响应性能。根据DO的估计值，在反步控制器中加入补偿项，从而提高系统的自抗扰能力；在控制系统中，采用电压外环与电流内环的级联结构，将控制器分为直流电压控制子系统和无功电流控制子系统两部分。针对二阶的直流电压状态方程，采用该方法逐步设计控制器。分析Lyapunov函数可以证明闭环系统是稳定的。搭建仿真系统验证所用控制方法的有效性。分析仿真结果可以得出，本文采用DO估计干扰项，提高了抑制扰动的性能，同时采用基于DO的反步控制所设计的控制器增强了SVG系统的动态响应效果。

1 SVG数学模型

采用的电压型PWM整流器的SVG无功补偿拓扑结构如图1所示。

图1 基于SVG的无功补偿装置拓扑结构Fig.1 Topology of reactive power compensation equipment based on SVG

SVG在两相旋转坐标系（dq坐标系）下的数学模型为

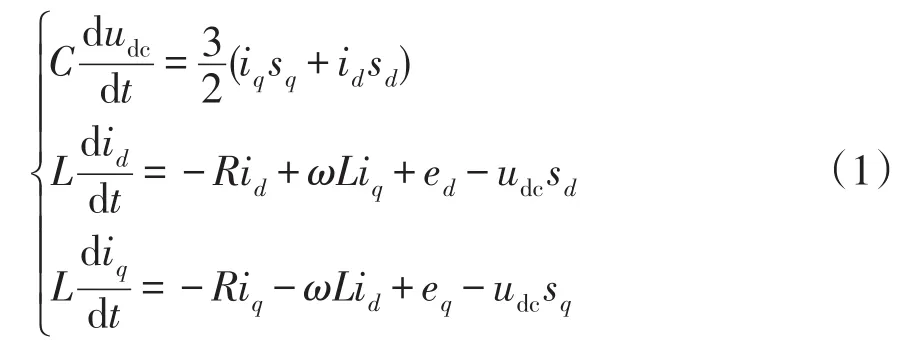
式中：C为直流侧电容的电容值；udc为SVG直流侧的电压值；id和iq分别为SVG交流侧电流在dq坐标系中的d轴分量和q轴分量；sd和sq为变换到dq坐标系下的开关函数；L为连接电抗器的电感；R为电抗器的等效电阻；ω为电网角频率；ed和eq分别表示电网电压的d、q分量。从式（1）可以看出，SVG系统为非线性系统，其非线性体现为控制输入与系统状态变量的乘积耦合关系。为便于控制器的设计，采用一种准线性化的方法。当忽略三相桥路自身损耗、采用等量坐标变换时，SVG交流侧有功功率与直流侧功率相等。令

式（1）可改写为[21]

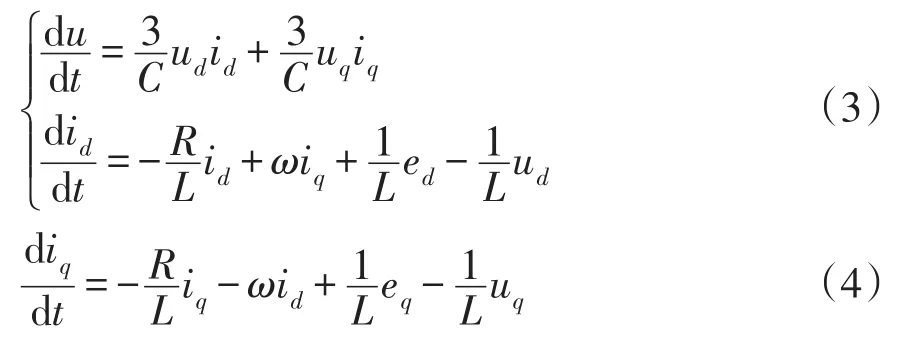
式（3）和（4）在形式上为线性系统，但是考虑上述的变量代换，即式（2）、（3）和（4）本质上仍为非线性系统，因此式（3）和（4）被称为准线性系统[22]。变量代换只是形式上的线性化，并没有改变系统非线性的本质，此处使用变量代换的目的是便于控制器的设计。

从式（3）和（4）可以看出，本文将SVG的控制系统分为两部分：一部分为直流电压控制子系统，其控制目标为维持SVG直流侧电压稳定，保证SVG可以正常运行；另一部分是无功电流控制子系统，其控制目标是根据负载所需的无功电流，控制SVG交流侧输出电流补偿负载无功电流。因此，为使SVG能够补偿电力系统无功功率、提高功率因数，需设计合适的控制器以保证SVG的性能。

2 控制器设计

2.1 直流电压控制器设计

当考虑外部扰动的影响时，将方程（3）改写为

式中：ψ1=3ud/C；f1=3uqiq/C；ψ2=-1/L；f2=-Rid/L+ωiq+ed/L；d1和d2为系统的恒定扰动。

令跟踪误差为ξ1=uref-u，其中uref为状态变量u的给定值，则

式中，f1为系统扰动。为了估计系统扰动与外部扰动，设计一个扰动观测器DO1如下：

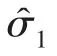
使用DO1的估计值，设计抗扰控制器，

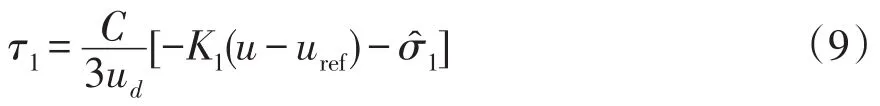
式中，K1为控制器增益。带入式（6）得到

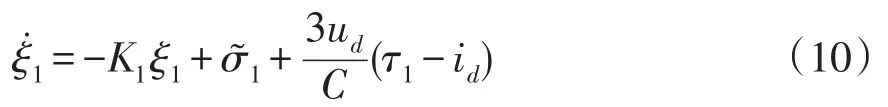
定义状态变量跟踪误差ξ2=τ1-id，并求导

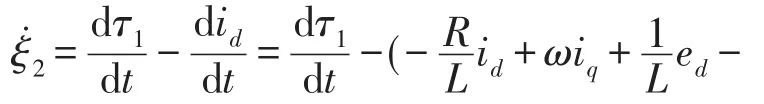
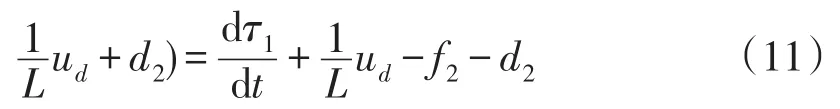
将f2设为系统扰动，并设计DO2估计总扰动

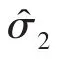
同时根据估计值，可设计控制律

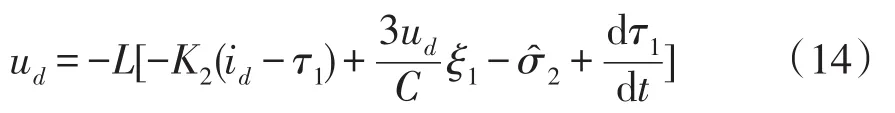
式中，K2为控制器增益。带入式（11）中，可得

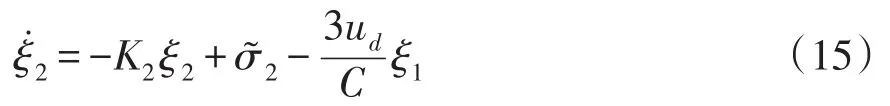
在上述的控制器设计中，DO1和DO2被用来估计系统的总扰动，并根据估计值，逐步设计控制律，最终得出d轴电压的给定值。由上述的设计过程可以得出直流电压控制子系统的结构如图2所示。

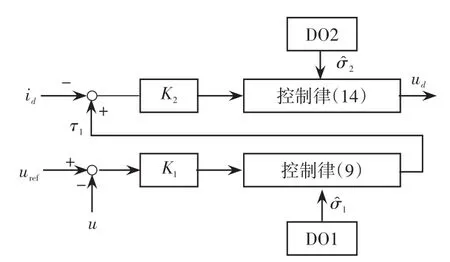
图2 直流电压控制子系统结构Fig.2 Structure of sub-system under DC voltage control

2.2 无功电流控制器设计

由基尔霍夫电流定律可知，电网电流、负载端电流以及SVG交流侧电流的关系为isd=id+ild，isq=iq+ilq，式中isd和isq为电网电流的dq轴分量；ild和ilq为负载端电流的dq轴分量。SVG的作用是产生补偿非线性负载的无功电流，以达到使电网无功电流为零，即isq=0的目的。因此，SVG输出电流的q轴分量的期望值应为iqref=-ilq。即通过控制SVG输出的q轴电流，补偿负载无功电流。

无功电流的跟踪误差为ξ3=iqref-iq，考虑外部的恒定扰动，其导数为

将 f3=-Riq/L-ωid+eq/L视为系统扰动，可设计DO3，对总扰动进行估计

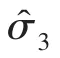
联立式（4）和（17），可得

考虑扰动补偿的控制律为

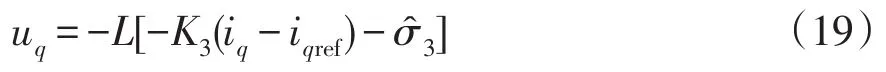
式中，K3为控制器增益。式（16）可改写为

无功电流控制结构如图3所示，控制器输出得到q轴电压的给定值。

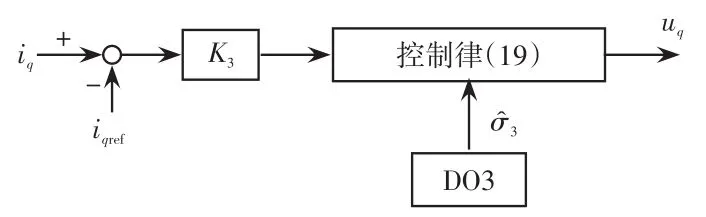
图3 无功电流控制子系统结构Fig.3 Structure of sub-system under reactive current control

综上所述，采用SVG进行无功补偿的整体结构包括主电路以及控制系统，其中SVG的控制系统分为两部分，即直流电压控制子系统和无功电流控制子系统。两个子系统分别输出给定值ud和uq，经过坐标变换后，得到两相静止坐标系中的给定值ualf和ubet，最后通过SVPWM技术，产生控制脉冲，驱动主电路中开关器件的动作，完成补偿无功的目标。

3 稳定性分析

由控制器的设计过程可知，本文将SVG控制系统分为了两个部分，因此分别证明直流电压子系统以及无功电流子系统的稳定性，就证明了系统的稳定性。

首先需要注意到，在实际系统中控制输入是有界的，即 udmin≤ud≤udmax, uqmin≤uq≤uqmax,其中，udmin、udmax、uqmin及uqmax为常数。并且对于系统扰动 f1、f2和 f3做出以下假设。

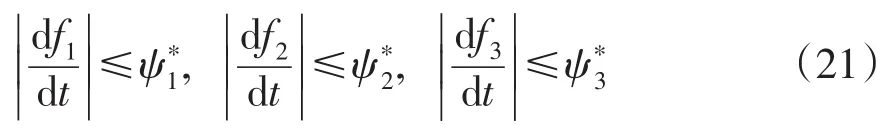
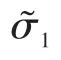
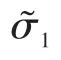
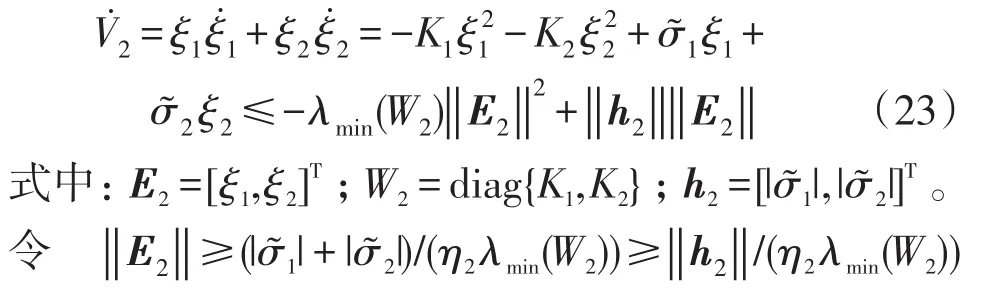
最后，对级联系统进行稳定性分析，该系统的级联关系表示为

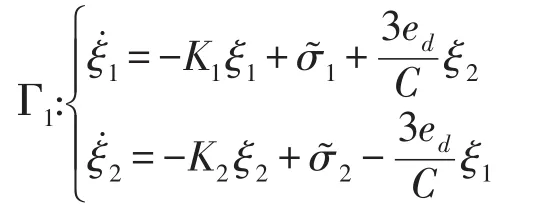
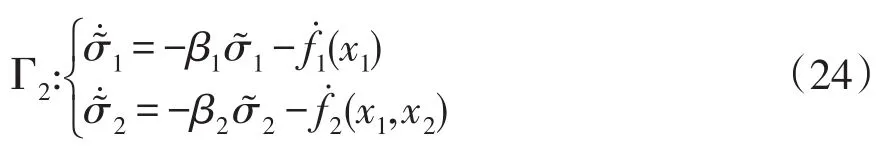
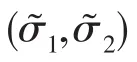
当采用基于扰动观测器的反步控制方法设计的参考输入值ud有界时，直流电压闭环级联子系统为一致最终有界。

同理，本文直接给出无功电流控制子系统稳定性分析的结论：当所设计的参考输入值uq有界时，无功电流闭环子系统一致最终有界。

4 仿真结果

本文使用Matlab/Simulink进行仿真验证。仿真系统主要分为主电路以及控制系统两部分，其中控制系统由直流电压控制子系统、无功电流控制子系统、SVPWM调制单元组成。主电路的相关参数如表1所示。

表1 主电路相关参数Tab.1 Parameters of main circuit

首先通过仿真验证SVG的无功补偿效果，在1 s之前电网接入有功功率为1 000 W，无功功率为1 000 var的阻感性负载；在1 s的时候，将负载换为有功功率为1 500 W、无功功率为800 var的阻容性负载。在保证系统稳定的前提下，借鉴文献[24]的参数设计方法，仿真中控制器的参数为K1=3 000；K2=12 000；K3=8 000。该控制器参数的选取使得直流电压快速跟踪给定值，具有良好的电流响应速度以及较小的稳态误差。图4给出了补偿后的电网电压电流波形。可以看出，无论是在阻感性负载还是在阻容性负载时，进行无功补偿后，电压与电流的相位差均被消除。切换负载的动态响应时间为0.03 s左右，在这个过程中，电网电流最大值由7.0 A变为10.2 A。分析图5中的直流侧电压的数据可知，直流侧电压稳定在600.0 V，在动态过程中，其下降到597.5 V后快速恢复到600.0 V，动态过程持续0.03 s。对比补偿前后的效果图，加入SVG后，SVG直流侧电压被控制在给定值，保证SVG的正常工作，交流侧输出了非线性负载所需的无功电流，获得了较好的无功补偿效果。

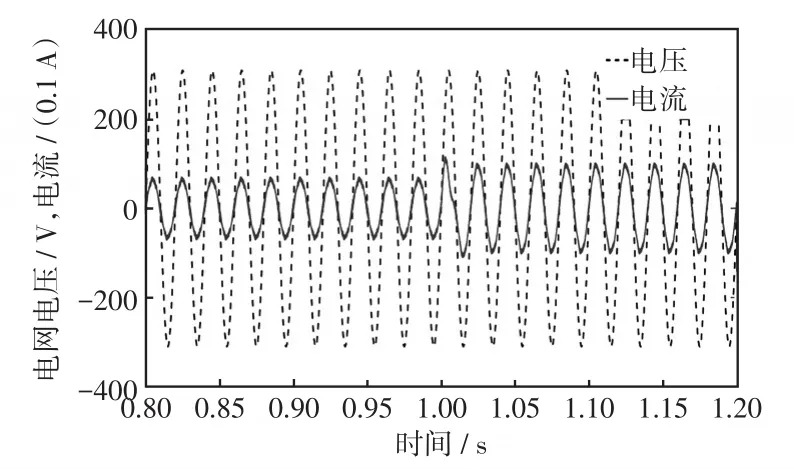
图4 补偿后电网电压电流波形Fig.4 Waveforms of grid voltage and grid current after compensation

图5 直流侧电压波形Fig.5 Waveform of DC-side voltage

为验证所用控制方法的优点，本文还进行了SVG投入前后电网电流以及功率因数的动态效果仿真，结果如图6和图7所示。在该组仿真中，SVG在0.6 s的时候投入，负载设置为阻感性，并且加入PI控制的仿真结果与之进行比较，在PI控制器中，电压外环的参数为K1p=2.5，K1i=12；电流内环有功电流控制器参数为K1p=12，K1i=60；无功电流控制器参数为K1p=1.5，K1i=8。并且本文给出的比较仿真的PI控制器参数为多次调试后选取的最优参数。分析仿真数据，本文采用的方法在动态过程中能够将功率因数保持在较高的水平上，动态过程持续时间为0.02 s。在图8中，比较了在切换负载时，本文采用的方法与PI方法的仿真结果，在切换负载的动态过程中，本文采用的方法将功率因数控制在0.95以上，保证了SVG的动态性能。

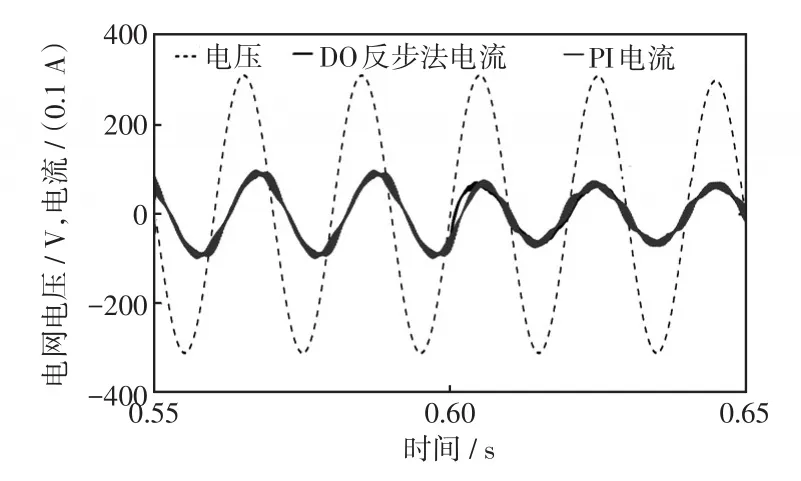
图6 电网电流动态波形Fig.6 Dynamic waveforms of grid current

图7 功率因数动态波形Fig.7 Dynamic waveforms of power factor

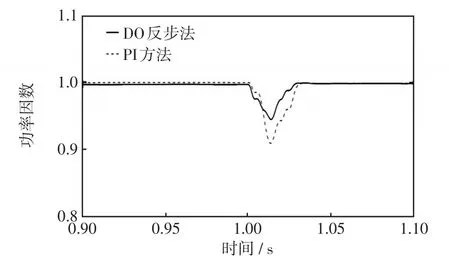
图8 补偿后功率因数波形Fig.8 Waveforms of power factor after compensation

本文设计的DO估计扰动项，以提高系统自抗扰能力，因此其跟踪真实扰动的效果对控制器会有较大影响。本文设计的观测器参数为β1=8 000，β2=250，β3=150。图9、图10、图11分别给出DO1、DO2、DO3观测对应扰动的结果图。并且在1 s时，使负载发生突变，需要观测的实际值也会随之变化。从图9～图11中可以看出，观测器的动态响应时间为0.05 s左右，具有较好的动态跟踪效果。因此基于扰动观测器输出的观测值设计的控制器具有良好的自抗扰能力。

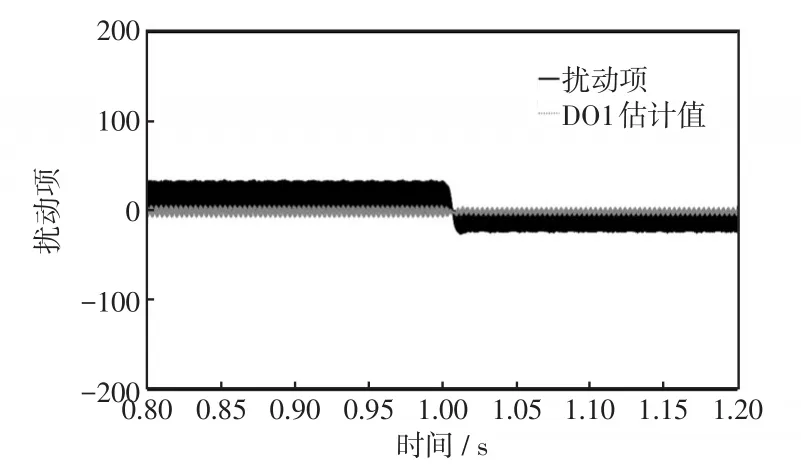
图9 DO1跟踪扰动项效果Fig.9 Tracking uncertainty effect of DO1

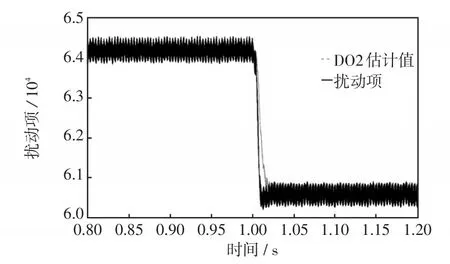
图10 DO2跟踪扰动项效果Fig.10 Tracking uncertainty effect of DO2

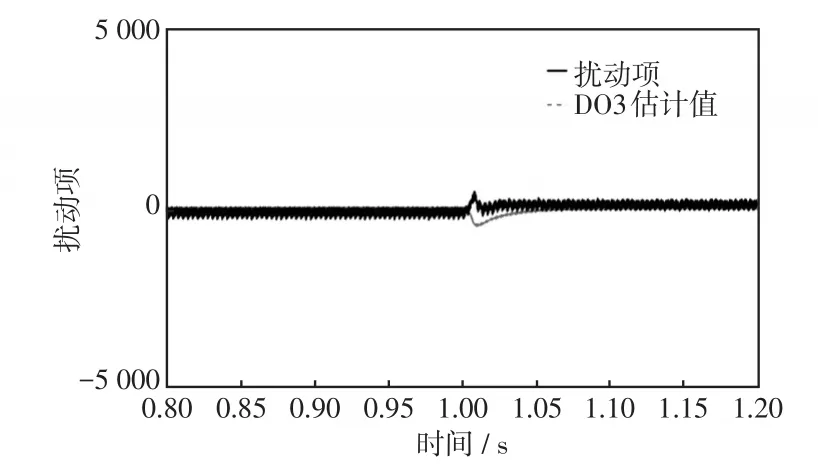
图11 DO3跟踪扰动项效果Fig.11 Tracking uncertainty effect of DO3

5 结语

本文采用基于DO的反步控制设计SVG控制器，提高了控制系统的自抗扰能力以及SVG的动态响应效果。在控制结构方面，本文采用了级联结构，电压外环与有功电流内环级联形成直流电压控制的二阶子系统，采用反步法的思路设计控制器，保证了SVG直流侧电压的稳定。同时由无功电流环产生无功电流，补偿负载所需的无功电流。通过设计合适的控制器，电力系统功率因数提升到单位功率因数附近，电网电压与电流之间的相位差被消除。在设计控制器时，将参数不确定项以及外部扰动合并为总扰动项，设计DO对其进行估计，在控制器中加入补偿项提高系统自抗扰能力。分析仿真结果，可以看出所用方法的有效性，并且SVG的稳态性能以及动态响应效果均有所提高。