一种谐波量测点优化配置的两阶段算法

何 胜 ，杨 斌 ，俞 明 ，肖 园 ，吕干云

（1.国家电网有限公司，北京 102209；2.国网江苏省电力有限公司，南京 210024；3.国网南京溧水区供电公司，南京 211200；4.南京工程学院电力工程学院，南京 211167；5.国网江西省电力有限公司经济技术研究院，南昌 330043）

近年来，随着非线性负荷在用电负荷所占比重日益增长以及电力系统电力电子化，大量谐波注入电力系统所造成的安全、经济影响日益严重[1]。谐波状态估计根据有限点上的谐波量测信息估算出未知节点及整个系统的谐波状态从而为谐波源的治理提供依据，而状态量估计精度和量测设备的数量及位置有关[2]。谐波量测装置HMD（harmonic measurement device）的高昂成本以及现代互联电力系统的规模化，使得谐波量测装置很难覆盖全网。因此，目前优化配置的核心问题仍是将最少的谐波量测装置布置在最合适的节点。

Heydt[3]首次提出谐波状态估计技术，考虑量测方程的数值稳定性，以系数矩阵的最小条件数进行谐波量测点最优配置，但是最小条件数法仅确定了最少量测配置数量，并未对配置的位置进行说明；文献[4-5]同时计及投资成本和状态量的估计精度，应用遗传算法求解二者的加权多目标数学模型得到量测最优配置，但是该算法迭代次数多且收敛速度较慢；文献[6]利用谐波源的稀疏性，在已有量测点的基础上利用网络拓扑可观性分析方法实现了新增量测点的最优配置。文献[7]考虑实际电力系统中各次谐波权重不同，以各次谐波平均迹值最小为目标，应用粒子群算法得到适合多次谐波的一组综合最优配置。但文献[6、7]均未给出电网可观条件下的具体配置方案以及量测装置数量；文献[8]在满足系统可观的前提下，以量测装置最少为目标，根据节点出线度的差异提出了概率偏移二进制粒子群算法，既提高了算法的收敛速度也能够同时生成多种量测方案，但并未进一步分析各个可行方案的优劣性。本文针对一般量测配置算法生成方案单一以及未对生成的多组方案进一步综合研究评估，使得最优方案在实际不可行时未能够及时给出次最优方案，提出了一种两阶段谐波量测配置算法：第一阶段应用改进二进制粒子群优化MBPSO（modified binary particle swarm optimization）算法求解得到多组可行方案；第二阶段在已有的多组配置方案中，考虑节点谐波电压对谐波注入电流的变化程度以及安装成本确定一组最优配置方案。

1 谐波量测配置基本原理

目前，谐波状态估计的可观性分析问题大都延用了传统状态估计[9-10]的基本方法，主要分为数值法和拓扑法两大类：数值可观性分析方法通过比较量测矩阵的秩与状态量个数的关系来判断是否可观，需要注意的是若量测量数目少于状态量个数，则各节点的谐波状态是不完全可观的，量测量数目大于状态量个数也不一定完全可观，这是因为量测矩阵各行之间可能会出现线性相关；拓扑可观性方法核心思想是检查已配置量测集和网络拓扑的关系，如果该配置集能够建立一个满秩的支撑树覆盖全网的节点，则该配置集是拓扑可观的。

为了以最少的经济投入得到尽可能多的量测信息，谐波量测点配置规则[11]有：①已配置量测装置的节点，其电压与连接到该节点的每条支路电流都能被量测；②若某支路一端已配置量测装置，则另一端的节点电压可由基尔霍夫电压、电流定律计算得到；③某节点仅有一条支路电流未知时，可由基尔霍夫电流定律计算得到。

2 基于MBPSO的第一阶段配置

2.1 第一阶段优化模型

本文初步量测配置目标就是在满足系统完全可观情况下选择所需谐波量测装置数量最少的方案，其目标函数和约束条件为

式中：x(i)=1表示在节点i处安装同步相量量测装置，x(i)=0则表示不安装；aij为关联矩阵A的元素，当节点i与节点j相连接或为同一点时，aij=1，否则，aij=0；B为n×1的单位矩阵。

2.2 改进二进制粒子群算法

为了更好地将二进制粒子群算法[12-15]应用于量测优化配置算法，本文提出的改进二进制粒子群算法主要表现在以下方面。

2.2.1 粒子更新机制

粒子更新机制Ⅰ：结合谐波量测配置规则①、②，若某节点已配置谐波量测装置，则与该节点相连接的节点都可观，即所需量测配置数目一定不超过系统总节点数的一半。若随机产生的初代粒子中量测配置数量过多会导致算法计算时间变长且收敛速率降低。因此，初始化期间确定量测装置总数的最大限制为

粒子更新机制Ⅱ：根据谐波量测配置规则②、③，若某节点已安装谐波量测装置，则所有与该节点相连的节点都变得可观，没有必要在其相连节点布置HMD。以简单5节点系统为例，图1中节点3已安装量测装置，位置更新时若同时选中节点2、4和5作为量测配置点集，会大大增加HMD数量；同样若节点2、4和5已配置HMD，那么节点3已无需再配置。

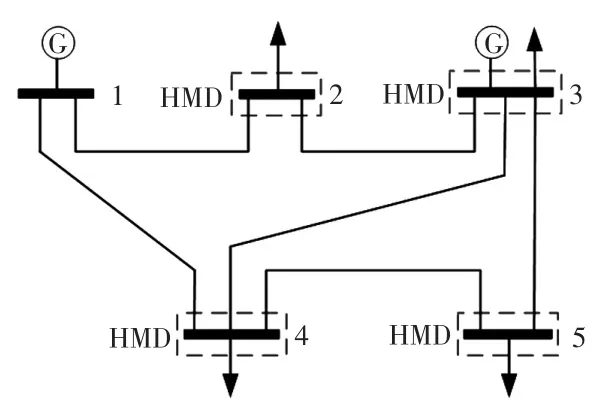
图1 5节点系统Fig.1 Five-bus system

这些类型的粒子不仅会增加运算时间，而且可能使得结果很难达到全局最优。考虑电力系统某些末端节点出线数较少，本文删除出线数少于3的节点对应关联矩阵A所在的行，形成A*。因此，本文提出的滤波机制Ⅱ为

若粒子在迭代过程中满足滤波机制Ⅱ，该粒子将会被重置。

2.2.2 指数型惯性因子

惯性因子ω通过平衡算法的开发和探索能力以控制粒子的搜索速度，较大的ω使粒子具有较强的全局探索能力，较小的ω使粒子具有较强的局部开发能力。本文所采用指数衰减的惯性因子为

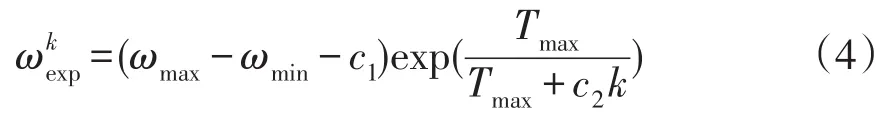
式中：c1和c2为控制因子，用以控制ωexp的下降速率；Tmax为最大迭代次数；ωmax和ωmin分别为惯性因子的最大和最小值。

根据谐波量测配置规则制定两个粒子更新机制能够提高运算效率和优化收敛性、采用呈指数衰减的惯性因子能够提高粒子群前期的搜索能力，防止过早收敛陷入局部最优。

3 计及估计精度及经济性的二阶段配置

第一阶段在满足电力系统谐波状态完全可观条件下能够得到多组谐波量测配置方案数目相同的可行方案，所以在实际电网中可进一步对多组可行方案进行评估。

3.1 谐波权重

谐波注入电流随着谐波频率的增加而减小，因此，较低频率的谐波所获权重系数应大于较高频率的谐波。为了定量表示谐波权重系数，本文采用优序图法PC（precedence chart）确定权重系数，根据文献[16]所提供的的谐波源数据，以5、7、11和13次谐波为主，计算出各次谐波权重系数为：σ5=0.208，σ7=0.194，σ11=0.153，σ13=0.125，σ17=0.097，σ19=0.083，σ23=0.056，σ25=0.056，σ29=0.028。

3.2 综合敏感因子

谐波注入电流对各节点谐波电压的影响程度用敏感因子表示，具有较高敏感因子的节点受谐波畸变的影响较大。因此，优先在敏感因子高的节点安装谐波量测装置，可以根据有限点上的谐波量测信息估计准确度更高的全网谐波状态。

根据节点法，节点谐波电压与谐波注入电流的关系可以表示为

式中：I为节点注入谐波电流；U为节点谐波电压；Y为谐波导纳矩阵；Z为谐波阻抗矩阵；下标h为谐波次数。

仅考虑单谐波源作用时，j节点上注入h次谐波电流与i节点的h次谐波电压的关系为

定义谐波注入电流变化对节点谐波电压的敏感因子λij为

结合前文提出的各次谐波权重，各节点的综合敏感因子δi为

式中：H为谐波总次数；σh为h次谐波对应权重系数。

综合敏感因子反映了多次谐波对整个系统的综合影响程度，节点对系统的谐波畸变影响程度与综合敏感因子大小呈正比。所以，选择在综合敏感因子较大的母线安装谐波量测装置能够提高谐波状态估计精度。

3.3 目标函数

一阶段配置得到多组可行方案的谐波量测装置数相同且已确认，因此第二阶段安装成本不计及谐波量测数量的成本，换言之，第二阶段的安装成本为支路量测通道成本。定义第二阶段安装成本与综合敏感因子加权和为工程成本，旨在找出一组安装成本低且综合敏感因子高即工程成本最低的方案。为消除二者在量纲上的差别，以各目标与其本身的极大值之比作为新的无量纲等级的目标函数，即

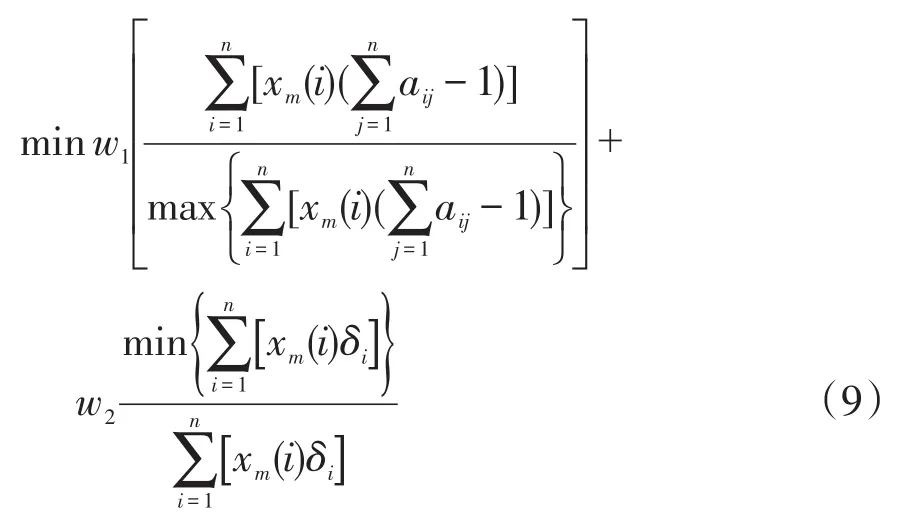
式中：m=1,2,…,L，其中L为一阶段所得可行方案总数；w1和w2为加权系数，支路量测通道成本远低于谐波量测装置成本，本文默认支路量测通道的成本与综合敏感因子同样重要，令w1=0.5，w2=0.5。

4 实验结果及分析

在Matlab9.1环境下开发了改进二进制粒子群算法，算法参数设置为：控制因子c1=0.2，c2=6；惯性因子上、下限 ωmax=0.94，ωmin=0.38；最大迭代次数 Tmax=100；种群规模为1 000。

4.1 IEEE14节点系统仿真

IEEE14节点系统的结构拓扑如图2所示。

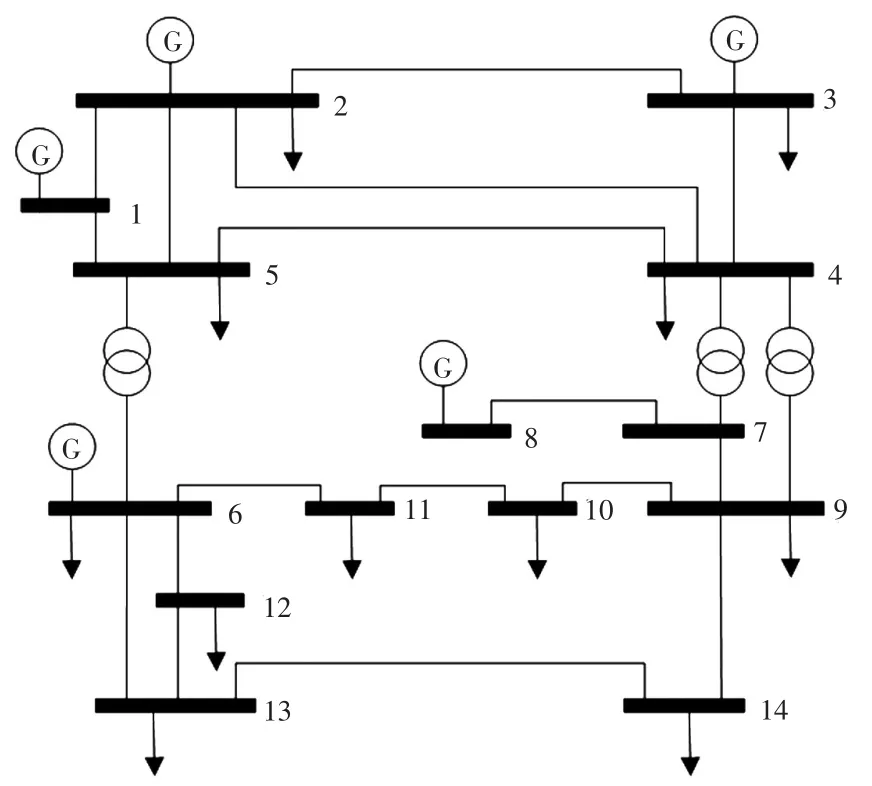
图2 IEEE14节点系统Fig.2 IEEE 14-bus system

对IEEE14节点系统的谐波量测优化配置问题分别采用BPSO、混合蛙跳算法[17]HFLA（hybrid frog leaping algorithm）以及本文所提MBPSO算法求解。上述3种方法经过重复仿真50次，收敛性对比曲线如图3所示，在系统节点规模数不大时，上述算法的收敛速度并无明显的差别。

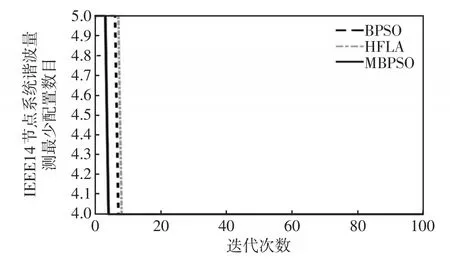
图3 IEEE14节点系统BPSO、HFLA与MBPSO收敛性对比Fig.3 Comparison of the convergence performance of IEEE 14-bus system among BPSO，HFLA，and MBPSO

第一阶段算法能够为14节点系统提供5种备选方案，在满足可观前提下所需最少量测配置数为4，约为系统总节点数的1/3。两阶段算法得到量测配置方案比较结果如表1所示，优先选择方案Ⅳ。虽然方案Ⅲ和Ⅳ安装成本相同，但是后者综合敏感因子较前者高，即所需同样的量测通道数，方案Ⅳ的选取有利于提高状态估计的精度。

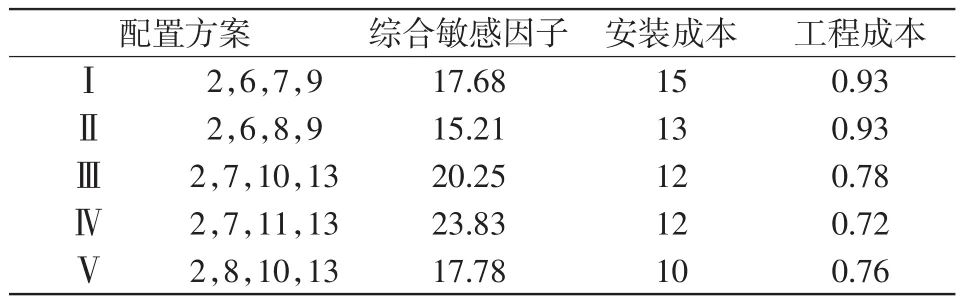
表1 IEEE14节点系统优化配置方案Tab.1 Optimal configuration schemes for IEEE 14-bus system

4.2 IEEE30节点系统仿真

IEEE30节点系统的结构拓扑如图4所示。收敛性对比的平均迭代曲线如图5所示。

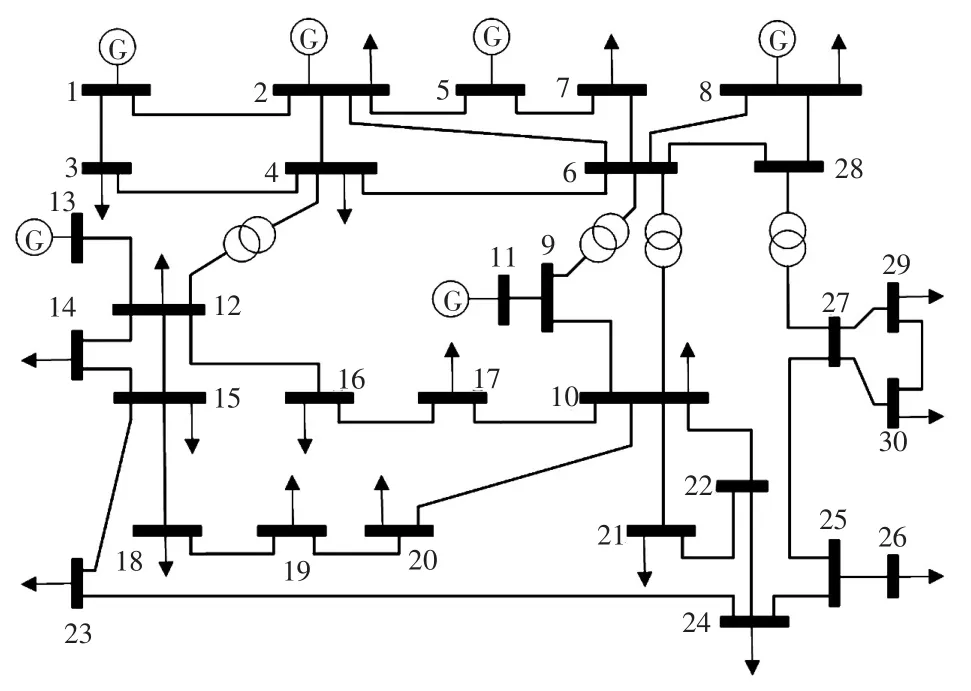
图4 IEEE30节点系统Fig.4 IEEE 30-bus system

对比图3和图5，随着系统规模的增大，第一阶段MBPSO算法具有更快的收敛速度。将种群规模分别设置成100、500和1 000，试验100次能够得到最少配置方案的成功率如表2所示。由表2中可见，3种算法的成功率随着种群规模增大而增大；在不同种群规模时，MBPSO的成功率明显高于其他两种算法，种群规模较小时也能够有较高的成功率。由图5和表2可以看出，第一阶段MBPSO算法相比其他两种算法在收敛速度和收敛方向方面表现更佳，而且能够为决策者提供更多可行的方案。

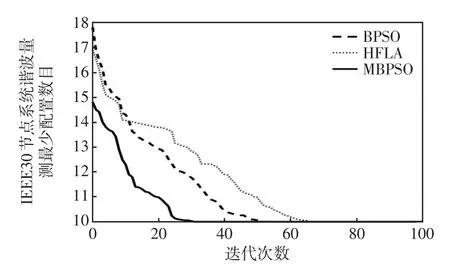
图5 IEEE30节点系统BPSO、HFLA与MBPSO收敛性对比Fig.5 Comparison of the convergence performance of IEEE 30-bus system among BPSO，HFLA，and MBPSO

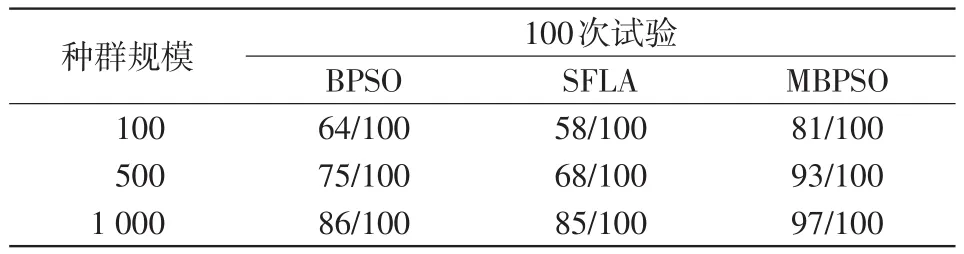
表2 IEEE30节点系统MBPSO性能分析Tab.2 Performance analysis of IEEE 30-bus system using MBPSO

第一阶段算法能够为30节点系统提供132种备选方案，在满足可观前提下所需最少量测配置数为10，是系统总节点数的1/3。两阶段算法得到量测配置方案比较结果如表3所示，限于篇幅，本文仅列出具有代表性的10组方案，优先选择方案Ⅰ。方案Ⅹ综合敏感因子较大，但是相比于方案Ⅰ，其安装成本高出15意味着需要额外安装15条支路电流量测通道，虽然一定的冗余度会增加估计精度，但是对于实际工程来说谐波状态估计的主要目的是将谐波源定位到节点而不需准确计算出谐波状态，因此，方案Ⅰ更具有实用性和经济性。

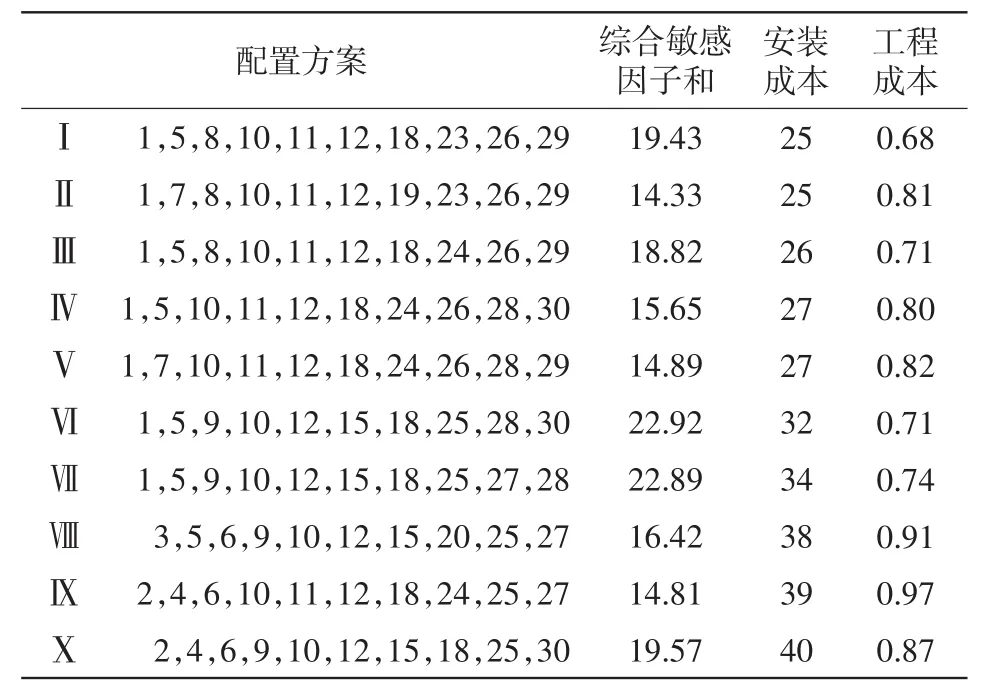
表3 IEEE30节点系统优化配置方案（部分）Tab.3 Optimal configuration schemes for IEEE 30-bus system（part）

5 结语

针对谐波量测点优化配置问题，本文提出了一种两阶段优化算法。仿真实验结果显示，该算法在第一阶段配置时能够快速且准确地得到更多组谐波量测装置数量最少的方案；第二阶段配置确定安装成本最低且对谐波电流变化具有高灵敏度的最优方案，在实际工程中遇到某节点无法安装量测装置时能够提供其他可行方案，具有一定的经济性和实用性。当然，实际中往往存在一定的谐波阻抗参数分散性和不确定性，今后将进一步研究适应不确定性的谐波量测点鲁棒优化配置。